正确解读2017年高考数学考试大纲中删去的“几何证明选讲”内容
2017-09-03深圳市第二实验学校518021李平
深圳市第二实验学校(518021) 李平
正确解读2017年高考数学考试大纲中删去的“几何证明选讲”内容
深圳市第二实验学校(518021) 李平
我们要正确解读2017年高考数学考试大纲中删去的“几何证明选讲”内容,“几何证明选讲”内容不是不考了,而是考得更加隐蔽了,更加灵活了,更加有深度了.这就要求我们老师在平时的教学和复习备考当中,充分应用平面几何知识去化解立体几何和解析几何的难度,从而解决问题.
几何证明选讲 立体几何 解析几何 化解 难度
在2017年3月进行的广州一模考试中,同学们普遍反映第19题(立体几何试题)中的第(2)小题不太容易得分,从考后的试卷分析来看(总共统计了两个学校,1043位学生),该题满分12分,学生均分只有4.13分,难度系数是0.34.一般来说,难度系数小于0.4是难题,大于0.7是容易题,在0.4和0.7之间属于中等题.本来应该属于中档题的立体几何试题,同学们得分率偏低的问题到底出在哪里呢?下面我们来共同分析一下这道试题[1].
题目 (2017年广州市普通高中毕业班综合测试(一),理科数学19题)如图1,在直角梯形ABCD中,AB与BC平行,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.
(I)求证:AB⊥平面ADC;
(II)若AD=1,二面角C−AB−D的平面角的正切值为求二面角B−AD−E的余弦值[3].
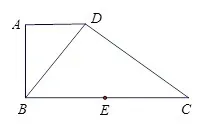
图1
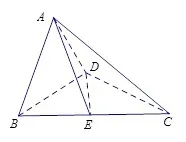
图2
分析 该题的第(1)小题比较简单,要证线面垂直,只需证如果两个平面互相垂直,在一个平面内垂直于它们交线的直线必垂直于另外一个平面即可.
第(2)小题是求二面角的余弦值,我们可以采用向量法和传统几何法,但不论采用哪种方法,建立空间直角坐标系还是做辅助线构造二面角的平面角,对大多数同学来说,都应该是不困难的,对同学们来说最大的问题是如何确定线段AB、BD和BC的长.解决这个问题是顺利做出本小题的关键.
而解决这个问题只需要观察折叠前的图形,得出△ABD~△BDC,利用相似比和勾股定理很容易求出AB、BD和BC的长,从而顺利解决第(2)小题.
学生的第(2)小题得分率之所以偏低,我们通过对学生的访问和分析,发现学生对平面几何证明中的相似比和勾股定理的灵活应用还存在很大的问题,学生应用的意识比较差,计算的能力不够强.这进一步说明,在平面几何证明的教学中,我们还存在很大的漏洞,缺乏有效的训练.
有些老师说,2017年高考数学考试大纲中不是已经删去了“几何证明选讲”内容吗?确实正如这些老师所说,随着新一轮高考和课程改革的逐步推进,在公布的2017年新高考数学考试大纲中,三个选考模块中删去了“几何证明选讲”模块,其余两个选考模块的内容和范围不变,考生从“极坐标和参数方程”,“不等式选讲”两个模块中任选一个作答[4].
虽然三个选考模块中删去了“几何证明选讲”模块,也就是说,“几何证明选讲”模块不再单独作为一道试题出现在新高考试卷中,但并不意味着“几何证明选讲”内容不考了,学生不用学习了,教师也不用再讲了.在2017年新高考试卷中,“几何证明选讲”内容将会以更加隐蔽的形式潜伏在其它试题当中,比如融入到立体几何试题和解析几何试题当中.
因此,在高考复习备考中,虽然“几何证明选讲”不再作为选考模块,但是由于新课程改革以来,初中对平面几何教学要求的降低和弱化以及相隔时间较长造成的遗忘,我认为除了要讲“极坐标和参数方程”,“不等式选讲”两个选考模块外,一定要讲“几何证明选讲”模块,千万不要因为2017年高考数学考试大纲中三个选考模块删去了“几何证明选讲”模块,而对他熟视无睹,否则在以后立体几何和解析几何复习考试当中,将会对学生造成极大的障碍和困扰.同时,在高三的第一轮复习当中,建议把“几何证明选讲”这部分内容,融入到立体几何和解析几何的专题复习当中,增强同学们解题的灵活性和应用性.
所以,我们要正确解读2017年高考数学考试大纲中删去的“几何证明选讲”内容,“几何证明选讲”内容不是不考了,而是考得更加隐蔽了,更加灵活了,更加有深度了.这就要求我们老师在平时的教学和复习备考当中,充分应用平面几何知识去化解立体几何和解析几何的难度,从而解决问题.
附 2017年广州市普通高中毕业班综合测试(一),理科数学试题19,两种解答方法:
解 (I)因为平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,又BD⊥DC,所以DC⊥平面ABD.因为AB⊂平面ABD,所以DC⊥AB.又因为折叠前后均有AD⊥AB,DC∩AD=D,所以AB⊥平面ADC.
(II)由(I)知AB⊥平面ADC,所以二面角C−AB−D的平面角为∠CAD.又DC⊥平面ABD,AD ⊂平面ABD,所以DC⊥AD.依题意因为AD=1,所以设AB=x(x>0),则依题意 △ABD ~ △BDC,所以即解得故
向量法1 如图3所示,建立空间直角坐标系D−xyz,则D(0,0,0),所 以
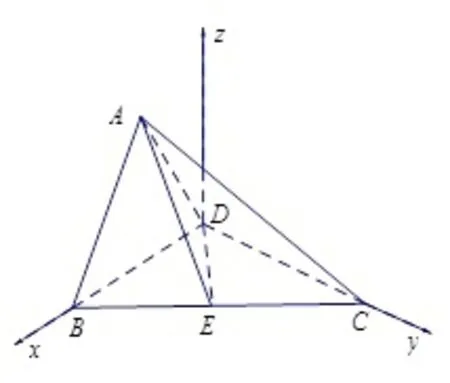
图3
由(I)知平面BAD的法向量n=(0,1,0).设平面ADE的法向量m=(x,y,z).由

得

几何法2 如图4所示.因为DC⊥平面ABD,过点E作EF平行DC交BD于 F,则 EF⊥ 平面 ABD.因为AD ⊂平面EFG,所以EF⊥AD.过点 F作FG⊥AD于 G,连接 GE,所以 AD⊥ 平面 ABD,因此AD⊥GE.所以二面角B−AD−E的平面角为∠EGF.
由平面几何知识求得


图4
所以
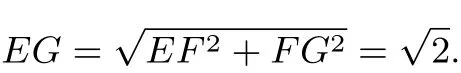
为进一步说明,充分应用平面几何知识去化解立体几何和解析几何的难度,从而解决问题,我再举例一个利用平面几何知识化解解析几何难度的试题[1].
题目2(2014年大纲全国卷,理科数学21.)已知抛物线C:y2=2px(p>0)的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且
(1)求C的方程;
(2)过F的直线l与C相交于A,B两点,若AB的垂直平分线l′与C相交于M,N两点,且A,M,B,N四点在同一圆上,求l的方程.
(2)通过题设分析判断直线l与x轴不垂直.因直线l过F(1,0),可设l的方程为x=my+1(m/=0).直线l与抛物线方程联立,利用韦达定理得到y1+y2,y1y2关于m的表达式,借助弦长公式得(其中A(x1,y1),B(x2,y2)),同理可得(其中M(x3,y3),N(x4,y4)).由题目中的A,M,B,N 四点在同一圆上得到关于m的方程,进而求出m,得到直线l的方程.
解法一 (1)设Q(x0,4),代入y2=2px,得所以
(2)依题意知l与坐标轴不垂直,故可设l的方程为x=my+1(m/=0).代入y2=4x,得
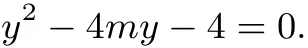
设A(x1,y1),B(x2,y2),则

故线段AB的中点为D(2m2+1,2m),

又直线l′的斜率为−m,所以l′的方程为
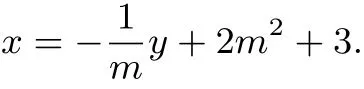
将上式代入y2=4x,并整理得

设M(x3,y3),N(x4,y4),则
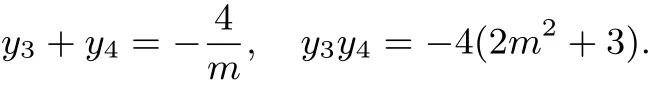

由于线段MN垂直平分线段AB,故A,M,B,N四点在同一圆上等价于从而即化简得m2−1=0,解得m=1或m=−1,故所求直线l的方程为x−y−1=0或x+y−1=0[5].
分析二 (1)考查抛物线的定义与方程,借助于p的几何意义及抛物线的性质确定p.
(2)如何简洁地表达“A,M,B,N四点在同一圆上”这一关键条件是解决问题的重难点.事实上,选择利用直线的参数方程,通过相交弦定理来表达共圆就可以轻松化解这一难题,并且可以用此方法得到更一般的结论.
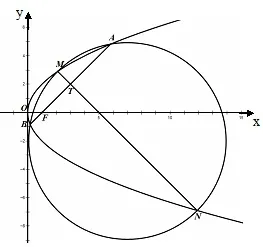
图5
解法二 (1)略(同解法一)(2)如下图5所示,设直线AB的倾斜角为α,因为AB⊥MN,直线MN 的倾斜角为90◦+α,又直线MN 与直线AB相交于T(x0,y0),则直线AB的参数方程为
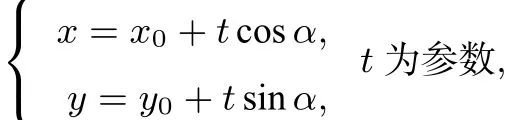
直线MN的参数方程为,

即为

将直线AB与抛物线C:y2=4x联立,有(y0+tsinα)2=4(x0+tcosα),即

由韦达定理得,

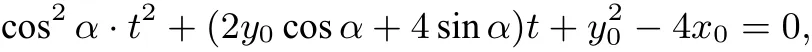

从而由相交弦定理,有|TA|·|TB|=|TN|·|TM|,因此,于是 tan2α =1,tanα = ±1,即α=45◦或α=135◦.故所求直线l的方程为x−y−1=0或x+y−1=0.
此外,一般地,在对称轴与坐标轴平行或垂直的非圆二次曲线上取四点P,Q,M,N,且直线PQ与直线MN的斜率均存在,那么P,Q,M,N四点共圆的充要条件是直线PQ与直线MN的斜率互为相反数.
第(2)小题的解法二,无论从形式和计算量来看,都比解法一要简洁的多,由此,我们可以发现,学会充分应用平面几何知识去化解立体几何和解析几何难度的重要性.
[1]何小亚,2016年数学高考全国I卷的认知分析和备考及命题建议[J],中学数学研究,2016(10).
[2]兰琦,高考数学压轴题的分析与解[M],杭州:浙江大学出版社,2016.
[3]2017年广州市普通高中毕业班综合测试(一)理科数学,2017.
[4]2017年普通高等学校招生全国统一考试大纲[S],北京:高等教育出版社,2016.
[5]2014年普通高等学校招生全国统一考试(全国大纲卷)理科数学,2014.
