赏析2016年北京大学自主招生数学试题

山东省东营市烟台路胜利第一中学(257027) 李加军 吴盛盛

赏析2016年北京大学自主招生数学试题

山东省东营市烟台路胜利第一中学(257027) 李加军 吴盛盛

近日偶得2016年北京大学自主招生考试全部数学试题,相比2015年的5道选择题和5道填空题,2016年试题形式变为20道选择题,数量增加一倍,结构全部为主观题,內容涉及函数、方程、多项式、三角、数列、不等式、平面几何、复数、排列组合、数论等,覆盖面广泛,风格迥异,内容灵活,给人耳目一新的感觉.试题难度虽然不是太大,但需要基本功扎实,思维灵活,且具备一定的课外延伸能力.下面笔者给出试题的详细解答,与各位读者共同欣赏.

2.点P位于△ABC所在的平面内,使得△PAB、△PBC、△PCA的面积相等,则点P有( )

A.1个 B.3个

C.5个 D.前三个答案都不对

解 如图1,考虑到平面内使△PAB和△PBC的面积相等的点的轨迹为直线BM以及过点B且与AC平行的直线,其中M为边AC的中点.因此满足题意的点P有4个:△ABC的重心,或者由P,A,B,C四点所构成的平行四边形的顶点.故答案选D.

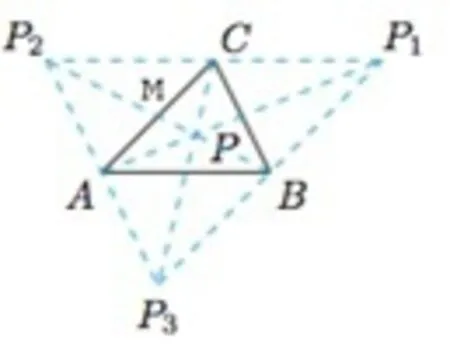
图1

3.圆内接四边形ABCD中,AB=136,BC=80,CD=150,DA=102,则它的外接圆直径为( )

A.170 B.180

解 根据四点共圆,其对角互补,由余弦定理得

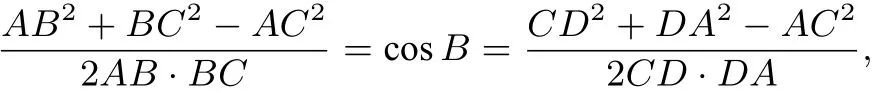
即

4.正方体的八个顶点中任取3个构成三角形,则三角形是等腰三角形的概率是( )

5.已知f(x)=3x2−x+4,g(x)为整系数多项式,f(g(x))=3x4+18x3+50x2+69x+a(a为常数),则g(x)各项系数之和为( )

A.8 B.4 C.2 D.前三个答案都不对

解 由题意可设g(x)=x2+bx+c(b,c∈Z),则f(g(x))=3(x2+bx+c)2−(x2+bx+c)+4=3x4+6bx3+(3b2+6c−1)x2+(6bc−b)x+4−c+3c2,与f(g(x))=3x4+18x3+50x2+69x+a比较系数得6b=18,3b2+6c−1=50,6bc−b=69,解得b=3,c=4,于是g(x)=x2+3x+4,各项系数之和为8,故答案选A.

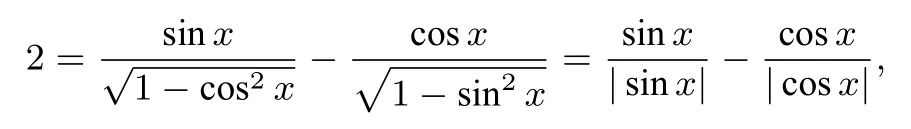
7.实系数方程x4+ax3+bx2+cx+d=0的根都不是实数,其中两个根的和为2+i,另两个根的积为5+6i,则b等于( )

A.11 B.13

C.15 D.前三个答案都不对

于是

故答案选C.

8.54 张扑克牌,将第1张扔掉,第2张放到最后;第3张扔掉,第4张放到最后,依次下去,最后手上只剩下一张牌,则这张牌在原来的牌中从上面数的第( )张.

A.30 B.32

C.44 D.前三个答案都不对

解 每一轮剩下的牌依次是2,4,6,..., 52,54;4,8,12,..., 52;4,12,20, ...,44,52; ...;12,28,44;12,44;44.故最后剩下的那张牌是原先的第44张牌.故答案选C.

9.(2+1)(22+1)···(22016+1)的个位数字为 ( )

A.1 B.3 C.5 D.前三个答案都不对

解 因为22+1=5,且对于任意正整数k,都有2k+1为奇数,所以 (2+1)(22+1)···(22016+1) ≡ 5(mod 10),故答案选C.

10.设S为有限集合,A1,A2,...,A2016为S的子集且对每个i,都有|Ai|≥|S|,则一定有S中某个元素在至少( )个Ai中出现?

A.403 B.404

C.2016 D.前三个答案都不对

解 设集合S中有n个元素,子集A1,A2,...,A2016中每一个都含有不少于个元素,即所有这些子集的元素个数和不少于由抽屉原理,一定有S中某个元素在至少+1=404个A中出现,故答案选B.i

11.四个半径为1的球两两相切,则它们外切正四面体的棱长为( )

D.前三个答案都不对

12.空间点集An定义如下:An={(x,y,z)∈R3:|3x|n+|8y|n+|z|n≤ 1},A=则由A中的点P组成的图形的体积等于( )

C.1 D.前三个答案都不对

解 当n→ ∞时,由|3x|n+|8y|n+|z|n≤1,只需要3x,8y,z∈(0,1)即可.因此所有满足要求的点P所形成的空间几何体为一个不包括边界的长方体,体积为

A.0 B.1001

C.2002 D.前三个答案都不对

14.已知对任意x1,x2,...,x2016,方程2016a在[0,4]上都至少有一个根,则a等于( )

A.1 B.2 C.3 D.前三个答案都不对

15.已知关于x的方程x2+ax+1=b有两个不同的非0整数根,则a2+b2有可能等于( )

A.一个素数 B.2的非负整数次幂

C.3的非负整数次幂 D.前三个答案都不对

解 设方程的两个根为x1,x2,则由韦达定理知x1+x2=−a,x1x2=1−b,于是于是a2+b2不是一个素数,又1+x2≡1或2(mod 3),所以不被3整除,而当x1=1,x2=−1时,a2+b2=22,故答案选B.

16.令an表示距离最近的正整数,其中n∈N∗,若则正整数n的值为( )

A.1015056 B.1017072

C.1019090 D.前三个答案都不对

解 设an=k,那么有即进而k2−k+1≤n≤k2+k.所以恰有2k个数等于k.于是且n=2m,解得1017072.故答案选B.

17.已知对于实数a,存在实数a,b满足a3−b3−c3=3abc,a2=2(b+c),则这样的实数a的个数为( )

A.1 B.3

C.无穷个 D.前三个答案都不对

解 a3−b3−c3=3abc⇔(a−b−c)(a2+b2+c2+ab−bc+ca)=0,而故a=b+c,或a= −b= −c,代入a2=2(b+c)得a=0,2,−4,故答案选B.

18.三角形ABC的三个顶点分别对应复数z1,z2,z3,已知=1+2i,则三角形ABC的面积与其最长边长的平方的比等于( )

19.将1,2,...,100这100个数分成3组,满足第一组中各数之和是102的倍数,第二组中各数之和是203的倍数,第三组中各数之和是304的倍数,则满足上述要求的分组方法数为( )

A.1 B.3 C.6 D.前三个答案都不对

解 假设这样的分法存在,设三组数的和分别为102x,203y,304z,x,y,z ∈ N∗,则 102x+203y+304z=5050,即101(x+2y+3z)+x+y+z=101×50,于是101|(x+y+z),因此x+y+z≥101.此时102x+203y+304z＞102(x+y+z)＞5050,矛盾.故答案选D.20.已知则(x−2016)(y−2016)(z−2016)=( )

A.0 B.1

C.不能确定 D.前三个答案都不对

所以

故答案选A.