地铁线路轨道中高频动态特性研究
2017-09-03吴海涛温泽峰池茂儒
吴海涛,李 伟,温泽峰,池茂儒
(西南交通大学 牵引动力国家重点实验室,成都 610031)
地铁线路轨道中高频动态特性研究
吴海涛,李 伟,温泽峰,池茂儒
(西南交通大学 牵引动力国家重点实验室,成都 610031)
地铁线路轨道中高频动态特性对轮轨振动噪声和钢轨短波长波磨的产生有重要作用。建立地铁整体道床轨道的三维实体有限元模型,结合现场力锤敲击法测试结果,计算分析地铁轨道的中高频动态特性,分析扣件刚度、轮对载荷对轨道中高频动态特性的影响。研究结果表明:普通扣件(垂向静态刚度约40 kN/mm)-整体轨道结构在150 Hz以下低频模态表现为轨道板和钢轨整体的垂向弯曲振动,在150 Hz~1 500 Hz中高频模态表现为钢轨相对于轨道板的弯曲振动、轨道板单独的弯曲振动和钢轨局部的扭转振动;扣件垂向刚度在10 kN/mm~40 kN/mm范围内变化对频率在750 Hz以下钢轨垂向动态特性有影响,对钢轨750 Hz以上的中高频模态振型影响不明显;轮对模态在1 500 Hz以下主要表现为弯曲和扭转振动,其对轨道的低频模态振型(钢轨和轨道板整体垂向弯曲振动)影响不明显,对轨道部分中高频模态(钢轨的垂向弯曲振动)影响明显。在400 Hz~1 100 Hz频率范围内,考虑轮对影响的轨道垂向模态频率增大,增大范围为10 Hz~56 Hz。
振动与波;地铁线路;整体道床轨道;有限元法;模态分析;中高频动态特性
随着我国城市轨道交通的快速发展,车辆轨道结构部件失效和振动噪声问题日益突显。在车辆载荷的作用下,轨道振动是导致以上问题的主要原因[1]。我国地铁出现的短波长钢轨波磨现象(激励轮轨冲击振动)和轮轨振动噪声问题均表现出中高频特性,其与轨道结构自身动态特性相关[2]。研究分析地铁线路轨道结构的中高频特性,对解决目前我国地铁车辆轨道结构损伤现象和振动噪声问题有重要意义。
国内外学者对轨道结构动态特性进行了大量的理论和实验研究。耿传智将模态分析理论应用于轨道结构振动特性的研究中,简化轨道振动的理论分析,使最终实现轨道定量分析成为可能[3]。涂勤明、雷晓燕等建立轨道-隧道-大地的三维有限元模型,分别对整体道床、弹性支承块道床和钢弹簧浮置板道床进行动力学分析,发现减振道床的自振频率对减振效果有较大影响[4]。苏云、吴天行等建立一种研究浮置板轨道横向运动的数值模型,考虑了钢轨的扭转变形,得到钢轨轨头以及浮置板在谐振作用下的横向位移响应以及钢轨扣件、钢弹簧的支承力[5]。尚文军等应用有限元理论和模态分析理论,研究钢轨的不同支撑条件对钢轨固有频率和振型的影响,研究表明不同的支撑方式对轨道模态参数有较大影响[6]。向俊等基于不同类型无砟轨道空间振动分析模型,分析比较系统振动响应随无砟轨道类型及车速的变化规律,发现无砟轨道类型对钢轨竖向位移、轨道板竖向位移等响应影响较大[7]。De Man等系统分析各种轨道结构的动力学特性和性能[8]。Knothe和Grassie介绍了轨道模型的建立,并利用频响函数分析轨道的高频振动特性[9]。李伟利用钢轨波磨线性分析模型对我国地铁线路不同轨道结构的钢轨波磨成因进行仿真分析,分析轨道结构的导纳特性与钢轨波磨特征的相关性,发现轨道出现低位移导纳值时对钢轨波磨形成和发展的影响尤为明显[1]。
目前对地铁轨道动态特性规律及其影响因素的研究还不够全面,文中结合现场力锤敲击法,利用有限元法,分析地铁线路轨道的中高频动态特性规律,调查扣件刚度和轮对载荷对整体道床轨道中高频动态特性的影响。
1 数值模型
对于无限长轨道系统,轮轨振动对轨道的影响区域有限,在保证数值计算精度条件下,还需节约计算时间,因而需要选择合理的轨道长度进行建模计算。文献[10]研究表明,对于较高频率的振动,轨道过短易引起附加共振及反共振,模型越短,附加共振及反共振点越多,要在模型中完全消除附加共振及反共振,模型长度至少要选取8个枕跨。文中选用20个枕跨长度的轨道结构模型进行计算,其足够满足各阶共振和反共振特性的计算要求。
以国内某条地铁线路为例,该地铁线路整体道床轨道结构主要由钢轨、扣件、长轨枕和轨道板组成。基于现场地铁轨道结构参数,利用有限元软件Abaqus建立整体道床轨道结构的三维实体有限元模型,如图1所示。

图1 长轨枕整体道床轨道结构有限元模型
道床、轨枕和钢轨采用三维实体单元模拟;扣件和路基采用弹簧和阻尼单元来简化模拟;轨道板的两端采用固定约束,钢轨两端为对称约束,因为钢轨模型的单元太多,设置对称约束便于减少计算量;地基支承刚度和阻尼使用单位面积单个节点的路基刚度和阻尼的计算值。数值模型中,轨道板和钢轨的长度为12.5 m,轨枕间距为0.625 m,单元类型主要是八节点六面体单元,在局部部位如扣件位置处采用细网格划分,最小网格大小为10 mm,因为扣件是轨道结构中钢轨和轨枕相互作用的部位,网格细化可更准确地模拟实际轨道受力状态。数值模型一共包含745 950个单元和867 281个节点。
此外,为了考虑轮对对轨道特性的影响,在原轨道模型的基础上建立轮对-轨道有限元模型,如图2所示。

图2 轮对-轨道结构有限元模型
模型中,在轨道的中央加入了一个轮对,轮对采用非刚体建模,轮轨间的接触通过赫兹弹簧模拟。该模型一共包含了个796 230单元和958 626个节点。轨道结构相关参数如表1所示。
2 结果与分析
首先对整体道床轨道结构进行模态分析。为了考虑轨道在中高频范围内(为目前地铁轮轨噪声和钢轨短波长波磨激励相关的频率)的动态特性,将模态分析的频率设置为1 Hz~1 500 Hz,一共提取轨道结构前400多阶的模态振型和特征值。同时调查轨道扣件刚度参数和轮对载荷对轨道动态特性的影响。
为了调查轨道动态特性,利用力锤敲击方法对整体道床轨道结构导纳特性进行现场测试,结果如图3所示。

表1 轨道结构参数

图3 轨道结构力锤敲击试验现场照片
力锤选用铝制锤头,激励的频带为0~2 kHz,激励力范围为300 N~1 000 N。激励力信号通过力传感器测试,轨道响应信号通过加速度传感器测试。加速度传感器分别安装在跨中轨头和轨枕上方轨头位置。每个测试点的加速度测试结果通过敲击5次平均得到。
图4给出根据力锤敲击法获得的轨道垂向激励响应测试结果,包括跨中激励、轨枕正上方和跨中钢轨响应的结果。可知:在1 200 Hz以内,轨道垂向明显的共振频率有 359 Hz、524 Hz、914 Hz和 1 030 Hz,且在小于200 Hz范围内没有出现共振峰,其中359 Hz、524 Hz和914 Hz处的响应幅值相当。这几个峰值频率所对应的模态振型都是钢轨相对于道床的垂向弯曲振动,见下文模态计算结果(见图5)。1 030 Hz处的振动响应为图中最高的共振峰,这是一个特殊的频率,它是关系到钢轨与扣件构成的周期性离散支撑结构特性而形成的特有共振频率,叫做Pinned-Pinned共振频率。

图4 力锤敲击轨道垂向激励测试结果
钢轨Pinned-Pinned振动模态是指支撑于两根轨枕之间的钢轨受到激励以后产生的纵向机械波,其驻波节点刚好在轨枕的支撑处,若按钢轨梁模型考虑,Pinned-Pinned振动频率可由理论公式(1)得出,钢轨Pinned-Pinned振动与钢轨的截面类型、钢轨重量以及轨枕间距有关[11]。此频率可以对轨道结构的设计工作起到指导作用,以控制轨道结构的振动与噪声。

式(1)中n为钢轨Pinned-Pinned振动阶数;a为轨枕间距(m);m为钢轨单位长度质量(kg/m);EI为钢轨竖向抗弯刚度(N∙m2)。
从模态分析结果中可找出与力锤敲击法测试获得的共振频率对应的模态振型,见图5。
图5(a)给出了357 Hz所对应的模态振型,该模态频率与实测结果359 Hz相近,这个振型为钢轨相对于轨道板(包括轨枕)的垂向弯曲振动,其振动波长横跨大约4个枕跨距离。图5(b)给出了1 025.6 Hz所对应的模态振型,该频率为轨道的1阶Pinned-Pinned垂向弯曲共振频率。

图5 轨道结构的振动模态
根据轨道结构垂向振型的不同特征状态,将地铁整体道床轨道结构模态按照频率分为低频和中高频两个频段,其界限频率的模态对应钢轨相对于轨道板开始发生垂向弯曲振动的情况[1]。图6(a)所示振型频率为141.4 Hz时轨道板、钢轨整体的垂向弯曲振动,其振动波长横跨约8个枕跨距离。图6(b)所示振型为频率等于151.5 Hz时钢轨相对于轨道板的1阶垂向弯曲振动,其振动波长横跨约10个枕跨距离。可知:在150 Hz以下,整体道床轨道结构模态表现为轨道板、钢轨整体的弯曲振动。
图7(a)为频率等于532.5 Hz时的钢轨相对于轨道板的横向弯曲振型,钢轨弯曲振动的波长约1.8个轨枕间距。图7(b)为频率等于1199.6 Hz时的钢轨相对于轨道板的高阶垂向弯曲振型,其中钢轨弯曲振动的波长约1.8个轨枕间距。图7(c)为频率等于757.5 Hz时的轨道板单独的横向弯曲振型。图7(d)为频率等于1446.4 Hz时的钢轨横向弯曲振动和轨底的弯曲扭转变形,且随着频率的增大,扭转振型出现得越来越频繁。
从以上结果分析可知,中高频段的轨道结构模态表现为钢轨相对于轨道板的高阶弯曲振动、轨道板单独的弯曲振动和钢轨局部的扭转振动;频率范围为150 Hz~1 500 Hz。钢轨相对于轨道板的弯曲振动占主体,且钢轨横向弯曲比垂向弯曲模态出现得更为频繁。
钢轨与轨枕间的联结是通过中间联结零件即钢轨扣件实现,扣件刚度大小对轨道弹性(即减振效果)和轨道结构固有特性有重要影响。分析不同扣件刚度对整个轨道结构动态特性的影响。数值模型中,扣件通过弹簧和阻尼单元模拟,通过变化弹簧单元的刚度即可实现扣件刚度的改变。
图8给出了根据力锤敲击法获得的普通扣件轨道和GJ3扣件轨道结构垂向激励响应测试结果。普通扣件和GJ3扣件的垂向静态刚度分别约为40 kN/mm和10 kN/mm。
由图8可知:
(1)轨道的Pinned-Pinned垂向弯曲共振频率不随扣件刚度的改变而改变;
(2)GJ3扣件轨道结构的频响曲线中出现139 Hz的峰值频率,此频率对应的模态振型是钢轨相对于轨道板的垂向弯曲振动,如图9所示。
刚度较大的普通扣件轨道结构频响曲线中没有出现类似频率,但模态计算结果中却表现出来,见图6(b)。这是由于扣件刚度较低,钢轨的低阶垂向弯曲易被力锤激发。对比图9与图6(b)可知,两图中钢轨弯曲振型不同,图9中钢轨振型的弯曲波长长。由此可见,扣件刚度的改变对钢轨垂向动态特性有影响;扣件刚度越小,出现相同振型的模态频率越小。

图6 轨道结构整体振动模态

图7 轨道结构中高频段的振动模态

图8 力锤敲击轨道垂向激励测试结果

图9 频率为138.12 Hz时模态振型
(3)频率大于750 Hz时两种轨道结构的频响曲线趋于相同,即随着模态频率的增加,扣件刚度对钢轨垂向动态特性的影响越小。
以上分析没有考虑轮对对轨道动态特性的影响。车辆运营时,轮对通过接触方式作用于轨道。而轮对与构架通过一系悬挂连接,由于一系刚度较低,构架和车体对轨道结构的中高频动态特性影响不明显,因而模态计算时仅考虑轮对对轨道动态特性的影响[12]。下面给出考虑轮对对轨道结构动态特性影响条件下的结果。
图10为轮对自身的固有模态,图(a)为车轴1阶弯曲模态,图(b)为车轮扭转弯曲模态,图(c)为车轮1阶弯曲模态。这些弯曲模态的存在,会使轮对和钢轨产生一些耦合振动模态,使得钢轨横向弯曲振动更加容易产生。图11为轮对和轨道静态接触作用后的固有模态振型。其中,图(a)给出频率为427.1 Hz时的轨道结构振动模态;其表现为车轮1阶弯曲振动和钢轨横向弯曲振动,且车轮和钢轨的模态是耦合在一起的。这种振型在频率在400 Hz~900 Hz之间的时候会发生;当频率变得更高时,钢轨的横向弯曲模态总会伴随着车轮的扭转弯曲振动,如图(b)所示,频率为956.7 Hz处的振动模态表现为车轮的扭转弯曲振动和钢轨的横向弯曲振动。图12给出了频率为442.3 Hz时的轨道模态,其表现为钢轨相对于轨道板的弯曲振动振型。该轨道结构模态振型和图11(a)所示振型相似,但是其模态频率比图11(a)中的频率值大15.2 Hz。
表2为考虑轮对影响和没有考虑轮对影响条件下的轨道结构中钢轨相对于轨道板发生垂向弯曲模态振动的频率对照表。图13为考虑轮对和没有考虑轮对影响条件下的轨道结构钢轨相对于轨道板发生垂向弯曲模态振动频率差值曲线。
由此可知:
(1)在频率范围为400 Hz~1 100 Hz内,轮对对钢轨垂向动态特性影响明显,其中频率差值最大达到56 Hz。这是由于轮轨间赫兹弹簧的作用,使得轨道结构整体的刚度发生了变化。
(2)在400 Hz以内和1 100 Hz以上的频段,轮对对于钢轨垂向动态特性的影响不明显。
分析结果表明,对于轨道结构的整体弯曲振动模态(即钢轨与轨道板同时发生弯曲振动),有无轮对的加入影响不明显,其模态频率和振型相差不大。图6(a)与图14中轨道板与钢轨一起发生相同的垂向弯曲振动,其中没有轮对载荷的振型频率为141.4 Hz,有轮对参与的振型频率为141.27 Hz,两个频率值相差较小。

图10 轮对振动模态

图11 考虑轮对影响条件下的轨道模态振型

图12 轨道结构在频率为442.3 Hz时模态频率振型

表2 考虑轮对和没有考虑轮对条件下的轨道结构模态频率统计表/Hz
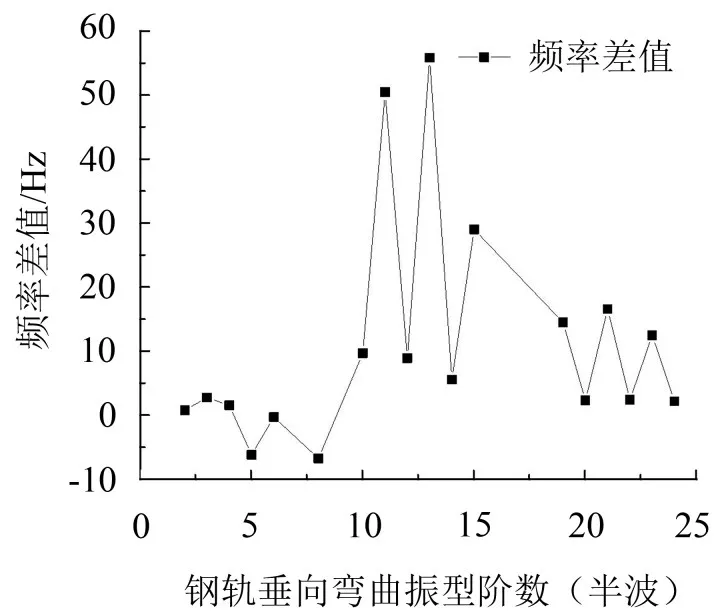
图13 轮对-轨道结构和轨道结构频率差值

图14 轮对-轨道结构在频率为141.27 Hz时模态振型
这是由于单个轮对的质量相对于整个轨道结构质量所占的比重很小,所以轮对对轨道结构的整体振型和频率影响较小。
3 结语
结合现场力锤敲击法测试结果,利用建立的地铁整体道床轨道的三维实体有限元模型,分析地铁轨道的中高频动态特性以及扣件刚度和轮对载荷对其的影响,得到以下结论:
(1)对于普通扣件(垂向静态刚度约40 kN/mm)整体道床轨道结构,轨道结构低频(150 Hz以下)模态主要表现为轨道板和钢轨整体的垂向弯曲振动;中高频段(150 Hz~1 500 Hz)模态表现为钢轨相对于轨道板的垂向弯曲振动、轨道板单独的弯曲振动和钢轨局部的扭转振动。钢轨相对于轨道板的弯曲振动占主体,且钢轨的横向弯曲比垂向弯曲振动出现得更为频繁。
(2)扣件垂向刚度在10 kN/mm~40 kN/mm范围内变化对频率750 Hz以下钢轨垂向动态特性有影响;扣件刚度越小,钢轨发生相同振型的振动所需要的激励频率也就越小,即钢轨的共振频率变小。扣件垂向刚度对钢轨750 Hz以上的中高频振动模态振型影响不明显。
(3)轮对模态在1 500 Hz以下主要表现为弯曲和扭转振动,其对轨道的低频模态振型(钢轨和轨道板整体垂向弯曲振动)没有影响,对轨道部分中高频模态(钢轨的垂向弯曲振动)影响明显。在400 Hz~1 100 Hz频率范围内,考虑轮对影响的轨道垂向模态频率增大,增大范围为10 Hz~56 Hz。在400 Hz以内和1 100 Hz以上,轮对对轨道的垂向动态特性影响不明显。
[1]李伟.地铁钢轨波磨成因及其对车辆/轨道行为的影响[D].成都:西南交通大学,2015.
[2]WEI LI,HENGYU WANG,ZEFENG WEN,et al.An investigation into the mechanism of metro rail corrugation using experimentaland theoreticalmethods[J].Proc IMechE Part F:Journal of Rail and Rapid Transit,2016,230(4):1025-1039.
[3]耿传智.模态分析在轨道振动特性研究中的应用[J].上海铁道学院学报,1995,16(1):13-24.
[4]涂勤明,雷晓燕,毛顺茂.地铁产生的环境振动及轨道结构减振分析[J].噪声与振动控制,2014,34(4):178-183.
[5]苏云,吴天行.浮置板轨道横向振动的谐响应分析[J].噪声与振动控制,2012,32(4):11-15.
[6]尚文军,张立民,梅桂明.轨枕间距对钢轨模态参数影响研究[J].噪声与振动控制,2008,28(2):44-46.
[7]向俊,赫丹,曾京.高速列车作用下不同类型无砟轨道振动响应分析[J].机械工程学报,2010,46(16):29-35.
[8]AMNON PIETER DE MAN.A survey of dynamic railway track properties and their quality[D].Brielle:Railway Engineering Group,2002.
[9]KNOTHE K L,GRASSIE S L.Modelling of railway track and vehicle/track interaction athigh frequencies[J].Vehicle System Dynamics,1993,22(3-4):209-262.
[10]魏伟.铁路轮轨系统高频振动[D].成都:西南交通大学,1997.
[11]孙方遒.不同频率钢轨的振动特性研究[D].北京:北京交通大学,2011.
[12]GUNMO GU,JUNGYOULCHOI.Thedynamic response of rail support[J].Vehicle System Dynamics,2013,51(6):798-820.
Study on Medium/High Frequency Dynamic Characteristics of Subway Tracks
WU Hai-tao,LI Wei,WEN Ze-feng,CHI Mao-ru
(State Key Laboratory of Traction Power,Southwest Jiaotong University,Chengdu 610031,China)
The medium/high frequency dynamic characteristics of subway tracks have important effects on wheel-rail vibration noise and short-wave-length rail corrugation.Based on the structure of subway monolithic track,the 3D finite element model of the track is established.Combined with the results of field hammering test,the medium/high frequency dynamic characteristics of the subway track are analyzed.The influences of the stiffness and the wheel load on the high frequency dynamic characteristics of the track are also investigated.The results show that:(1)For general fasteners(vertical static stiffness is about 40kN/mm)-overall track structure,the low frequency(below 150 Hz)modals demonstrate the overall vertical bending vibration of the track plate and the rail;the medium/high frequency(150 Hz-1 500 Hz)modals show the bending vibration of the rail relative to the track plate,flexural vibration of the track plate alone and torsional vibration of the rail.(2)The fasteners with 10 kN/mm-40 kN/mm vertical stiffness have some influence on the vertical dynamic characteristics of the rail only in the frequency range below 750 Hz.(3)The modals of the wheelset below 1 500 Hz frequency demonstrate mainly bending and torsional vibration.Fastener’s stiffness has little effect on the low frequency modals of the track(the whole vertical bending vibration of the rail and track plate).But it can affect part of the highfrequency modals obviously(vertical bending vibration of the rail).In the frequency range of 400 Hz-1 100 Hz,the frequency of the vertical modals of the rail with the effect of the wheelset considered increases by10 Hz-56 Hz.
vibration and wave;subway line;monolithic track bed;finite element method;modal analysis;medium/high frequency dynamic characteristic.
U213.2;U213.3
:A
:10.3969/j.issn.1006-1355.2017.04.027
1006-1355(2017)04-0138-06+196
2017-02-13
国家科技支撑计划资助项目(2015BAG12B01-16;2015BAG13B01-03)
吴海涛(1991-),男,江苏省东台市人,硕士研究生,目前从事轮轨接触动力学研究。E-mail:976755934@qq.com
温泽峰,男,研究员,博士生导师。
E-mail:zfwen@home.swjtu.edu.cn
