主动悬架LQG控制加权系数果蝇优化方法

李冰林，孙 宁

(南京林业大学 汽车与交通工程学院,南京 210037)

主动悬架LQG控制加权系数果蝇优化方法

李冰林，孙 宁

(南京林业大学 汽车与交通工程学院,南京 210037)

在汽车主动悬架LQG控制器的设计中，以悬架性能指标作为目标函数的加权系数通常为定值，为使系统性能达到更优，提出利用果蝇算法的参数少、易调节、计算量小、寻优精度高的特性，对其进行优化，提高LQG控制器的设计效率和性能。仿真结果表明，与传统的LQG控制结果进行对比，所采用的LQG控制果蝇优化权值系数方法更能改善汽车的主动悬架的性能。

振动与波；主动悬架；LQG控制；果蝇算法；加权系数

线性二次型最优控制算法(LQG)在主动悬架控制器的设计中应用最为广泛。该控制器中性能参数的加权系数往往直接影响到系统的控制指标和效果，通常的做法是由设计人员根据系统物理过程，依靠设计经验试凑来确定，这种选择权重系数的方法需要设计人员反复调试，费时费力，具有很强的主观性。如果参数选择不佳，会使得控制得不到最优的结果，甚至出现极大的偏差。目前，针对该问题处理的方法有通过遗传算法对权重系数进行优化，改善悬架性能[1–3]。陈双等人采用遗传粒子群LQG控制方法进行优化权重系数，也获得较好的优化效果[4]。

果蝇优化算法（Fruit Fly OptimizationAlgorithm，FOA）是潘文超教授提出的一种新的群智能算法，与其他群智能算法如粒子群算法相比，它是对1阶的方程进行优化，而粒子群采用的是2阶方程。因此果蝇优化算法相对简单，容易理解，易于编程实现，计算速度快，而且FOA只需调整初始值、种群大小和迭代步长等少数参数[5]。其它的群智能算法需要调整的参数达七、八个以上，多个参数之间的互相影响和耦合使得研究变得复杂，且算法的最终性能往往又是被这些参数的取值所决定。但是，FOA算法和其它全局优化算法类似，存在着陷入局部极点、出现早熟收敛的现象，特别是算法在处理复杂问题时。

文中提出一种基于果蝇优化LQG最优控制器权重系数的方法。其中，悬架控制器采用LQG算法，悬架的性能指标作为目标函数的加权系数采用果蝇算法进行优化。首先建立1/4车辆主动悬架的模型，设计优化的LQG控制器，通过仿真验证该优化控制方法的正确性和有效性。

1 主动悬架系统模型

选取二自由度的单轮车辆模型(如图1所示)为研究对象[6]。不考虑车辆轮胎变形过程中的阻尼变化，以线性弹簧代替弹性轮胎。

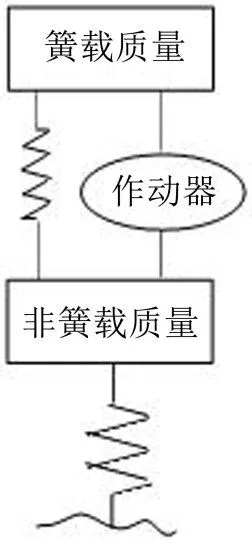
图1 单轮车辆模型

由牛顿运动定律,建立系统运动方程为

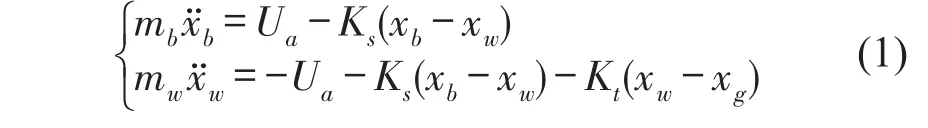
式中mb代表簧载质量；mw代表非簧载质量;Ks代表悬架刚度；Kt代表轮胎刚度；xb代表车身垂向位移；xw代表车轮垂向位移；xg代表路面垂向位移；Ua代表控制力。

假定路面不平度系数为G0；车辆行驶前进速度为u;高斯白噪声为w；下截止频率为f0。路面输入为滤波白噪声

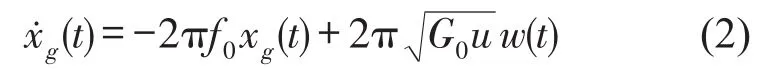
将悬架系统运动方程式(1)和路面输入方程式(2)以矩阵的形式表示，则系统的状态空间方程为

2 LQG控制器的设计

评价车辆悬架的性能主要指标包含：车身垂向振动加速度、轮胎动载荷、悬架动行程。因此LQG控制设计中的性能指标J即为此三个指标的加权平方和在时域T内的积分值，表达式为

式中q1、q2、q3分别代表轮胎动位移、车辆悬架动行程和车身垂向振动加速度的加权系数。

将式(4)改写成矩阵表达式，即

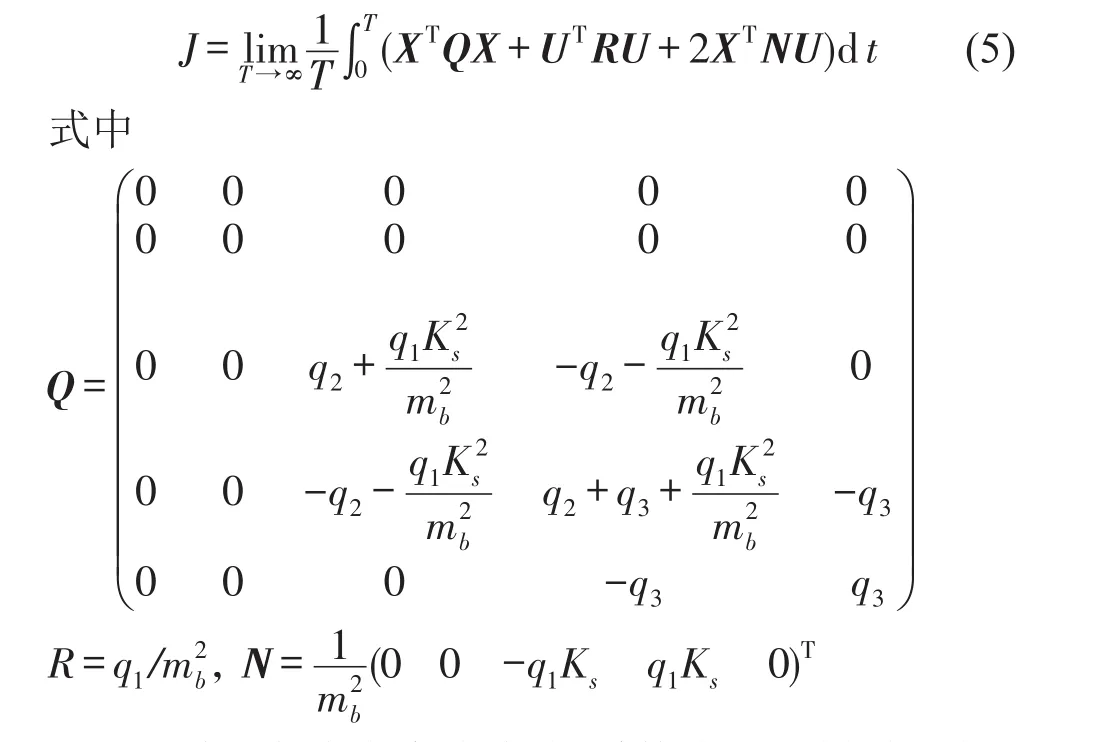
当确定性能指标的加权系数值后，最优控制反馈增益矩阵可由Riccati方程解出，表示为

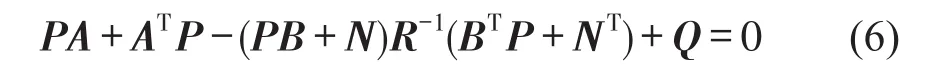
由式(6)可得系统最优反馈控制矩阵为K=BTP+NT，其值与车辆悬架系统参数和加权系数相关。在任意时刻t，根据反馈状态变量X(t)，就可以求出该时刻的最优控制力Ua，即

由此可知，当悬架参数选定后，根据以上方法所获得的最优控制反馈增益矩阵K完全归因于加权系数值的大小，而该系数的大小主要依靠设计者的经验反复试凑确定，由此获得的最优控制含有很多的主观因素。

3 果蝇优化算法

果蝇在嗅觉和视觉上优于其他物种，甚至能嗅到几千米以外的食物。FOA属于全局优化算法，该算法思路是根据果蝇搜集空气当中的各种气味，朝着食物所在的位置或者与同伴聚集的位置方向飞行。根据果蝇搜索食物的这种特性，果蝇优化算法有以下几步组成[7]：

(1)随机初始果蝇群体的位置X、Y

(2)果蝇个体相对初始位置飞行的随机方向与距离(Xi、Yi)。其中

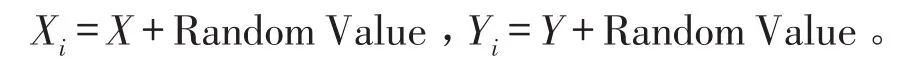
(3)计算食物与果蝇初始位置的距离估计值(Dist)，并求该值的倒数，然后计算味道浓度判定值(S)，见式（8）。

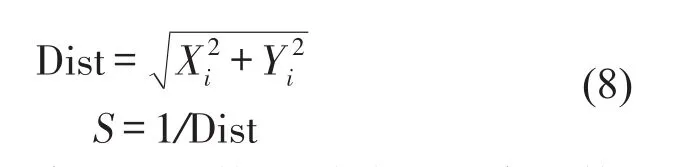
(4)获得味道浓度判定函数(或称为适应度函数)中的味道浓度判定值S后，分别求出每一个个体果蝇位置的味道浓度Smelli。

其中，Smelli=Function(Si)。

(5)求极大值，找出该群体中味道浓度最高的果蝇。其中[best Smellbest Index]=max(Smell)。

(6)保留此时X、Y的坐标和最佳味道浓度值，果蝇群体利用自身视觉飞往该位置。

其满足Smellbest=bestSmell，

X_axis=X(bestIndex)，Y_axis=Y(bestIndex)。

(7)最后重复执行以上步骤(2)至(5)，进行迭代寻优，若最新所得的味道浓度优于前一迭代味道浓度，则回到步骤(6)。

4 LQG控制加权系数优化算法

利用果蝇算法优化LQG控制加权系数可获得更真实的最优控制。性能指标由三个分量组成，分别是轮胎位移[xw(t)-xg(t)]2、悬架行程和车身垂向加速度由于它们的数量级和量纲都不同，故采用式(9)所表示性能指标的方式作为果蝇算法的适应度函数[8]，即

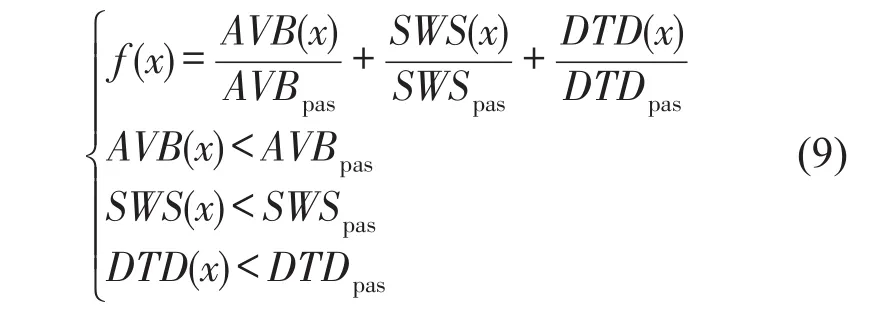
式中AVB(x)、SWS(x)、DTD(x)分别表示车辆主动悬架车身垂直加速度车辆悬架动扰度和轮胎变形量的均方根值；AVBpas、SWSpas、DTDpas分别代表车辆被动悬架的相应性能指标，优化变量x表示加权系数q1、q2、q3。

根据果蝇算法的优化过程和步骤，（流程见图2），整个计算流程是：

①计算出被动悬架性能AVBpas、SWSpas、DTDpas值；

②设置迭代次数，随机初始化果蝇群体的位置；

③初始化的果蝇个体利用嗅觉搜寻食物的随机方向与飞行距离；

④计算与原点Di之间的距离和味道浓度Si=1/Di；

⑤味道浓度乘以权重系数q1、q2、q3，并代入计算主动悬架LQG解，获得味道浓度判定值；

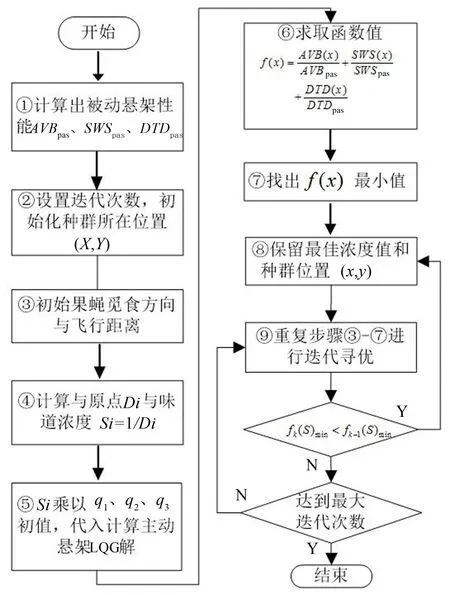
图2 果蝇优化算法流程图

⑦找出f(x)的最小值；

⑧保留最佳浓度值和种群位置；

⑨重复步骤③－⑦进行迭代寻优，使果蝇往该位置方向飞去，对比此次最小值和上次最小值，如果小于，最新所得的味道浓度优于前一迭代味道浓度，回到步骤⑧继续寻优，否则，是否达到迭代最大次数？如果是，程序结束，否则回到步骤⑨，继续寻优。

5 模型仿真及结果分析

5.1 参数选定

使用Matlab m文件编程的方法对LQG控制的主动悬架的工作性能进行仿真分析。1/4车辆的模型参数分别为：车身质量mb=320 kg，车轮质量mw=40 kg，悬架弹簧刚度Ks=20 kN/m，轮胎刚度Kt=200 kN/m，道路激励选择A级路面，路面输入如图3所示。

车速设定为20 m/s。加权系数的初值通常由经验决定，初值选自参考文献中的给定值，选取q1=80 000、q2=5、q3=1[9]。仿真采用Ode4(Runge-Kutta)解法，步长为0.001 s。

图3 路面激励信号

5.2 仿真分析

主动悬架LQG控制以及果蝇优化LQG控制权系数后的主动悬架性能指标均方根值如表1所示。由表1可知，优化后主动悬架的垂直加速度、悬架的动扰度和轮胎变形三个性能指标明显好于优化之前的对应数据。优化后的加权系数值分别为q1=24 161、q2=1.347 1、q3=0.376 2。

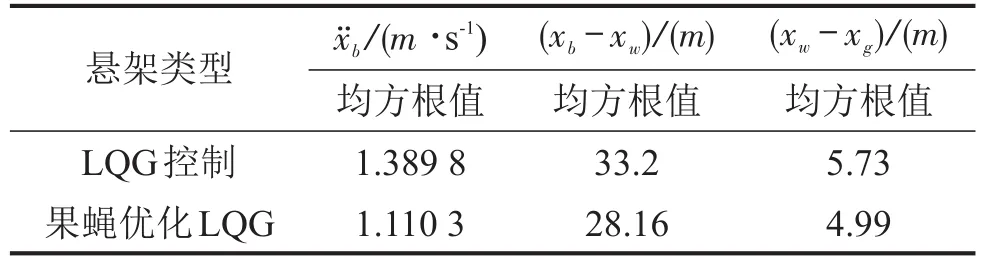
表1 性能参数对比

图4为迭代运算过程中果蝇位置的味道浓度变化曲线，由图4可知，大约经过50步的迭代，参数达到了稳定，算法收敛比较快，此时目标适应度函数式（9）达到最优，图5为果蝇群体寻优的行进轨迹。

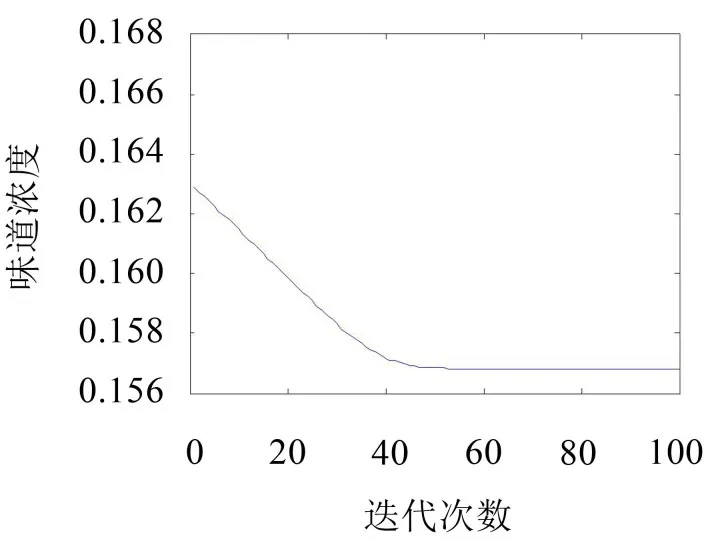
图4 迭代搜寻函数极大值曲线图

权衡汽车行驶平顺性的重要指标是汽车的车身加速度。对比图6－图7可知，果蝇优化LQG控制器加权系数后悬架的车身加速度峰值较小，其数值接近数据中心轴线的基数也偏小；而带有LQG控制器的主动悬架车身加速度接近数据中心轴线的基数大，故表1中车身加速度均方根值数据结果合理。与优化前的悬架车身加速度相比较，带有果蝇加权优化LQG控制器的主动悬架能有效降低汽车车身加速度，其均方根值减少12.91%，得到理想的控制效果。

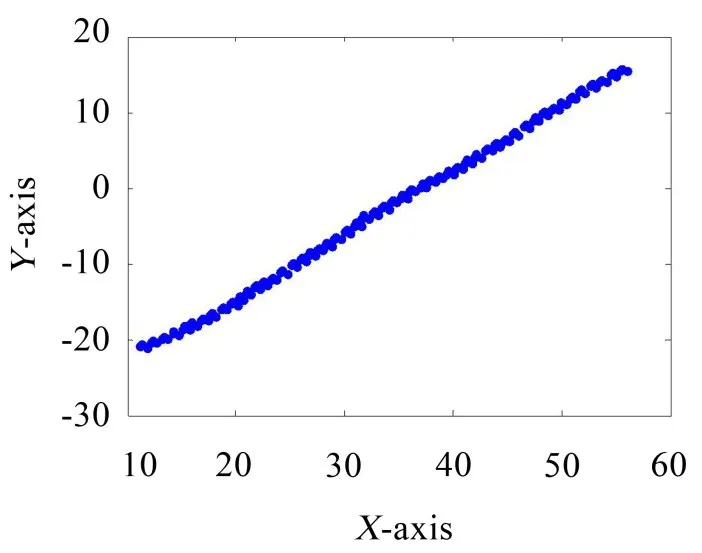
图5 果蝇群体寻优的行进轨迹

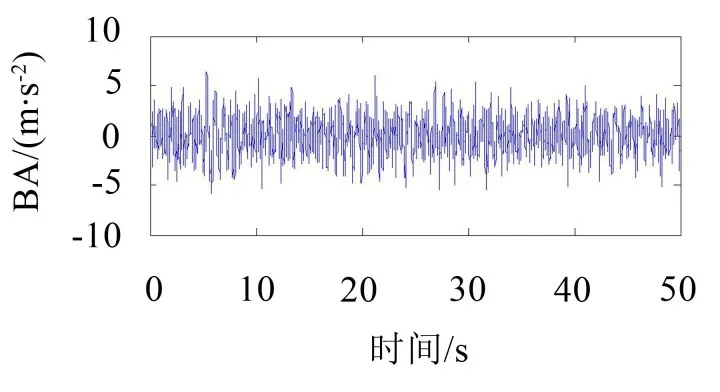
图6 LQG控制后的垂直加速度

图7 果蝇优化LQG控制权系数后的垂直加速度

同时，表1也反映了主动悬架LQG控制加权系数优化前后的悬架动行程响应的情况，在汽车悬架系统的设计中，因为与车身结构设计有关的悬架行程是有限的。文中所设计的悬架模型运行区间在±0.100 m之内，对比图8－图9可知，不管优化前后，采用LQG控制器的主动悬架能将悬架动行程控制在设计许可的行程内，悬架的工作空间得到充分利用。

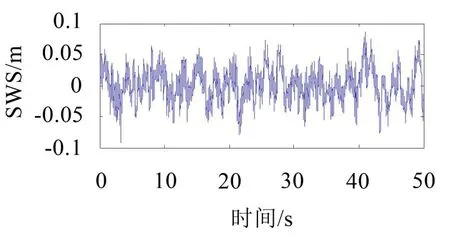
图8 LQG控制后的动行程

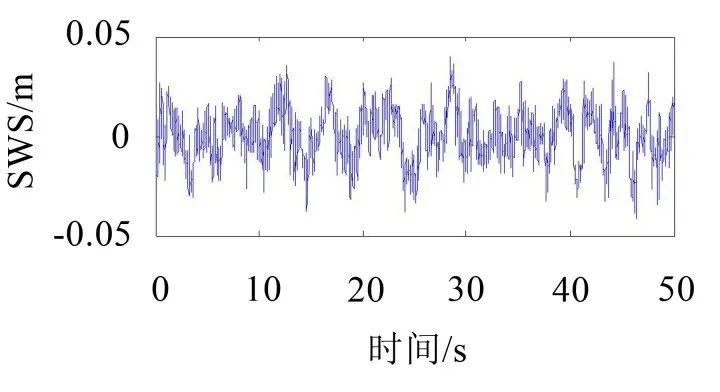
图9 果蝇优化LQG控制权系数后的悬架动行程

且通过表1可知，果蝇优化权值系数后主动悬架的动行程均方根值明显低于未被优化权值的主动悬架的值。对比LQG控制的主动悬架和果蝇优化加权系数后的LQG主动悬架系统可知，其均方根值减小15.18%，影响汽车性能指标的车身加速度和悬架动行程均有显著改善。

果蝇优化LQG控制权系数前后轮胎动载荷作用下的轮胎动位移如图10－图11所示。

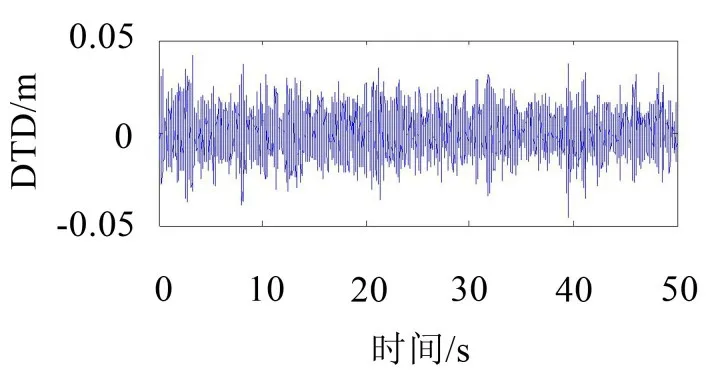
图10 LQG控制后的轮胎的动位移

图11 果蝇优化LQG控制权系数后的轮胎的动位移

轮胎的动载荷影响汽车的操纵稳定性，如果轮胎有相对稳定的垂直载荷，获得的轮胎抓地力会较大；相反，如果轮胎动载荷变化较大，则轮胎跳动频繁，跳动位移会增加，轮胎和地面间的接触性会变差，导致轮胎附着力减小，汽车操纵稳定性变差。且通过表1可知，采用果蝇优化LQG控制加权系数后的主动悬架与主动悬架LQG相比，其均方根值减小15.18%，能有效地抑制轮胎动载荷的波动。

6 结语

建立主动悬架的数学模型，以A级路面为激励，分别对采用LQG控制器的主动悬架和利用果蝇优化LQG控制加权系数后的主动悬架进行仿真研究，得出影响悬架性能的三项指标的数据。通过对主动悬架LQG控制优化加权系数前后性能指标的对比，验证基于果蝇优化加权系数的随机线性二次型最优控制策略的有效性。

[1]黄卫忠，高国琴.基于遗传算法的最优控制加权阵的设计[J].计算机测量与控制，2003，11(10)：761-762.

[2]胡斐，赵治国.主动悬架LQR控制加权系数多目标遗传算法优化[J].机械与电子，2011(2)：28-31.

[3]刘晓培.基于遗传算法的汽车主动悬架LQR控制器的优化设计[J].组合机床与自动化加工技术，2013(6)：78-80.

[4]陈双，宗长富.车辆主动悬架的遗传粒子群LQG控制方法[J].汽车工程，2015，37(2)：189-193.

[5]PAN WEN CHAO.Fruit flies optimization algorithm[M].Taiwan:Tsang Hai Book Publishing,2011.

[6]KIENCKE U,NIELSEN L.Automotive control systems.For engine,driveline,and vehicle[M].Berlin:Springer.2005.

[7]PAN W T.A new fruit fly optimization algorithm:taking the fnancial distress model as an example[J].Knowledge-Based Systems,2012(26):69-74.

[8]蓝会立，高远，谭光兴.车辆悬架LQR控制器权值优化方法[J].科学技术与工程，2013，13(17)：4833-4837.

[9]喻凡，林逸.汽车系统动力学[M].北京：机械工业出版社.2005：296-300.

Optimization of Weighting Factors for LQG Controller ofActive Suspensions Based on FOAAlgorithm

LI Bing-lin,SUN Ning
(College ofAutomobile and Traffic Engineering,Nanjing Forestry University,Nanjing 210037,China)

In the design of LQG controller for vehicle active suspension,the weighting factors of the objective function of suspension performance index are usually treated as a fixed value.In order to make the system performance better and improve the design efficiency and the performance of the LQG controller,the optimization method of weighting factors by using Fruit Fly Optimization Algorithm(FOA)is proposed.This method has the advantages of fewer parameters,less computer time consuming,high precision of optimization,and easy adjusting.The simulation results show that compared with the traditional LQG control,the proposed optimization method of weighting factors by using FOA of LQG control can improve the performance of the active suspension more effectively.

vibration and wave;active suspension;LQG control;fruit fly optimization algorithm(FOA);weighting factors

U463.33

：A

：10.3969/j.issn.1006-1355.2017.04.005

1006-1355(2017)04-0020-05

2017-01-03

江苏省高校自然科学基金资助项目（13KJB580006）；江苏省自然科学基金资助项目（BK20130977）

李冰林(1979－)，男，江西省安福市人，讲师，博士，主要研究方向为汽车电子控制技术。

E-mail:lbljdz@aliyun.com