含有输入时滞的悬架系统的最优控制

董天夫，方明霞

(同济大学 航空航天与力学学院,上海 200092)

含有输入时滞的悬架系统的最优控制

董天夫，方明霞

(同济大学 航空航天与力学学院,上海 200092)

伴随着主动控制环节的应用,悬架系统中不可避免会出现时滞因素。以含有时滞的2DOF主动悬架系统为研究对象，分别使用不考虑时滞的传统控制律和采用状态变换及系统离散化处理时滞后的控制律进行控制，并对控制系统的响应和稳定性特性进行对比。不考虑系统时滞时，直接采用传统的控制律进行控制，理论分析和数值仿真均表明：当时滞较小时，系统依然保持稳定，达到一定值时，可能引起系统响应定性特性改变，甚至失稳发散。采用状态变换的方法处理时滞后进行主动控制，能保证系统的稳定性，该控制律较好地反应了输入时滞对控制方程的影响。

振动与波；时滞系统；主动悬架；最优控制；数值计算

由于主动悬架能够根据车辆的行驶状态和路面状况作出主动响应，从而改善车辆行驶特性，提高车辆的乘坐舒适性和操纵稳定性，因此主动控制悬架受到国内外普遍重视。目前对主动控制悬架的研究主要集中在控制算法、稳定特性和试验方法等方面，对控制系统中的时滞分量的影响考虑较少。事实上，伴随着主动控制环节的应用，悬架系统中不可避免会出现一系列时滞因素，忽略时滞的影响可能会引起控制性能的下降，甚至导致系统定性特性的改变，因此考虑主动控制系统中时滞因素的影响势在必行。

目前已有部分学者对考虑时滞的主动控制系统进行研究，文献[1]根据二元机翼的力学模型，制定时滞反馈控制策略及建立控制系统的数学模型，并对系统进行稳定性分析，获得时滞反馈控制系统的颤振稳定性边界。文献[2]结合科茨求积分和线性插值的精细积分法，将时滞系统的状态方程引入到Hamilton体系中进行研究。依据最优滤波问题和带有时滞的观测器的双重准则，在全状态下对其方程进行精细积分求解。文献[3]研究单输入两时滞的离散系统的线性二次最优控制问题，将所研究的问题等价地转化成一个带约束条件的时滞问题，再转化成无时滞的条件极值问题进行求解。文献[4]设计基于动态输出反馈的鲁棒H–∞控制器，通过数值实例验证了该控制器对于参数摄动下的低频时变时滞悬架系统控制性能的有效性。文献[5]采用广义Sturm序列判别准则给出不同控制增益下单自由度车模型全时滞稳定区，并在给定时滞情况下绘出了控制增益稳定区。文献[6]在板梁结构时滞系统中采用一种新式时滞处理方法，将时滞因素直接引入反馈控制律中，成功实现系统的最优控制。

但由于汽车结构复杂，目前在汽车悬架主动控制的研究中极少考虑时滞因素的影响。为此文中以含有时滞的2DOF主动悬架系统为研究对象，分别采用传统控制律和处理时滞后的控制律进行控制，并分析悬架系统的稳定性。研究对主动悬架的动力学特性研究具有一定的参考价值。

1 两自由度车辆动力学模型的建立

车辆悬架系统是一个较为复杂的多输入多输出系统，为了研究方便，更好地与车辆实际行驶状况吻合，文中建立包括车身垂向运动z1和悬架非簧载质量垂向运动z2两个自由度悬架动力学模型，模型如图1所示。

图1 2DOF悬架动力学模型

利用第二类拉氏方程，得到系统的运动方程为

式中z1为悬架簧上质量垂向位移；z2为车轮受到的路面激励；m1为簧载质量；m2为非簧载质量；k2为轮胎的刚度；k1为悬架的等效刚度；c1为悬架等效阻尼；c2为轮胎阻尼；u(t-τ)为悬架的控制力。

采用带有低通滤波器的随机白噪声来模拟轮胎受到的路面激励

式中f0为下截止频率，取0.01；G0为路面不平度系数；U0为车速；ω1为路面输入白噪声信号。选择C级路面仿真，取G0=256×10-6，车速U0=20 m/s，仿真时间为10 s。生成的路面输入位移如图2所示。

仿真结果表明该仿真模型可以有效模拟不同等级的路面随机激励。

图2 C级路面仿真结果

综合式（1）、式（2），取c2=0 ，选取作为系统状态变量，系统的状态空间表达式为

2 主动控制悬架系统的稳定性分析

2.1 LQG控制器的设计

在控制器设计时，需综合考虑车身的位移加速度和悬架的动扰度等多个因素，在降低车身加速度的同时，应尽量保证悬架工作空间在系统允许范围内，以防止悬架撞击缓冲块。为此将悬架系统的目标函数确定为

式中q1、q2、q3、q4分别为车身垂向加速度、非簧载质量加速度、簧载质量位移和非簧载质量位移的加权系数。将式(1)中的代入式（4）中，则J的标准二次型形式为

式中Q为状态加权矩阵；R为控制力加权矩阵；N为交叉项权重矩阵。

当车辆参数值和加权系数值确定后，由Riccatti方程式(6)可求得其唯一正定解P

则最优控制反馈增益矩阵G=R-1(NT+BTP)。

根据最优控制理论可知，系统实际的最优控制规律为：U=-GX（t-τ)。

2.1 系统的稳定性分析

众所周知，引入时滞反馈控制后，反馈增益和时滞对系统的的稳定性有很大的影响，当系统无时滞量时，通过LQG最优控制可保证系统的稳定性，但加入时滞变量后就需要对系统的稳定性进行分析，将状态方程进行Laplace变换后得到

系统的特征方程为|A(s)|=0，即

若方程所有的特征根均具有负实部，则系统是稳定的。因此首先讨论系统临界稳定状态。

令s=wci(wc＞0)并代入方程，分离实部和虚部得到

现用l表示方程正实根的个数，当反馈增益g1取某一定值时，l的大小取决于方程系数di(i=0，2，4，6，8)。当l=0，方程无正实根，系统不发生稳定性切换。当l≠0，有每个wcm(m=1，...，l)对应着无限多个τ值当τ从τn-ε增加到方程特征根的变化趋势由下式确定。

RT=+1表示τ从左至右穿过临界值τn时，特征方程不稳定特征根的数量增加两个，RT=-1表示τ从左至右穿过临界值τn时，特征方程不稳定特征根的数量减少两个。基于以上的特征值分析，可以得到系统在一定反馈增益下的时滞稳定和不稳定区间。

根据上述过程对两自由度系统进行稳定性分析，系统参数如下：簧载质量m1=136.05 kg，非簧载质量m2=24.288 kg，悬架机械阻尼系数c1=153.11，悬架刚度k1=10 200 N/m，轮胎刚度k2=980 000 N/m。加权系数根据反复试算取q1=112 400，q2=1 000，q3=q4=1，得到反馈增益系数G=[3 023.9-57.7 57.7-293.7]，在这一确定的反馈增益系数下计算得到四个临界wc值，并计算得出系统在τ＞0.120 9 s时，系统变为不稳定，通过计算仿真得到如图（1）至图（5）所示的结果。

图1 当控制中含τ=0.04 s时簧载质量的位移

图2 当控制中含τ=0.06 s时簧载质量的位移

图3 当控制中含τ=0.10 s时簧载质量的位移

图4 当控制中含τ=0.12 s时簧载质量的位移

图5 当控制中含τ=0.14 s时簧载质量的位移

从图中可以看出，按照经典LQG方法直接得到反馈系数作用于系统中时，当控制力中含有的时滞较小时，系统依然能保持稳定，但当控制力中时滞较大时，则不可以直接采用二次型最优控制理论进行处理，否则将可能导致系统响应失稳发散。

为解决该问题，现对状态方程做如下变换

状态方程变为

式中B0=e-AτB。

根据二次型最优控制的理论得

从式（17）中可以看出，控制力的实现依赖于控制力中积分项的计算，令

设采样周期为T，并将时滞量表示为

式中l＞0为正整数；0≤m＜T，当m=0时，时滞量为采样周期的整数倍，当m≠0时，时滞量为采样周期的非整数倍。可以通过调整采样周期使时滞量为采样周期的整数倍，因此仅讨论m=0时的情况。

当数据采样周期较小时，在相邻的两个采样点间，控制力可按常值处理，即

U(k)实际上代表第k步控制U(kT)。为表达方便文中其他变量同此表达。当取t=kT时，即进行第k步计算时,经适当变换，式(18)变为

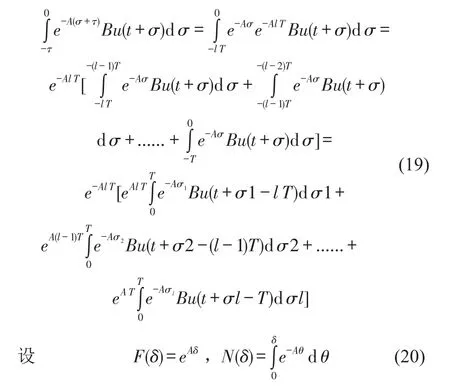
则式（18）可以写为

根据式(21)具体实现控制律时，每一步计算中除了包含有当前步的状态反馈外，还包含有前l步控制项的线性组合。

图6 当控制中含τ=0.12 s时簧载质量的位移

从图（6）中可以看出，按照上述时滞处理方法对系统进行转换，然后对系统施加控制律，可以有效地保证系统的稳定性。

3 结语

针对含有时滞的2DOF主动悬架系统，分别采用传统控制律和时滞处理后的控制律对悬架系统进行控制，并对系统的稳定性和响应特性进行分析，得到以下结论：

（1）若不考虑主动悬架中时滞变量的影响而直接采用传统控制律进行控制，可能引起系统定性特性的改变。当悬架系统中含有的输入时滞量较小时，控制系统仍能保持稳定，但当时滞达到一个较大值时，可能引起系统失稳。

（2）采用状态变换及系统离散化的方法，对含有时滞的悬架控制系统进行处理，设计含有时滞变量的二次型最优控制律。该控制律中除了包含当前的状态反馈外,还包含前若干步控制项的线性组合，较好地反映了输入时滞对控制方程的影响。

（3）通过对变换后的控制系统进行仿真，获得系统在临界时滞τ=0.12 s处的响应，相比于传统控制律作用下系统响应会发生发散的情况，变换后的控制系统在临界时滞处仍能保持稳定。研究表明优化后的控制规律能更好反映时滞对系统的影响。

[1]齐欢欢，徐鉴，方明霞.超音速飞行器机翼颤振的时滞反馈控制[J].应用数学和力学，2016，37(2)：210-218.

[2]师黎，邵帅飞.精细积分在时滞车辆悬架最优控制中的应用[J].计算机工程与设计，2009，30(19)：4516-4519.

[3]殷月竹.离散时滞系统的线性二次最优控制与仿真[J].黑龙江大学学报(自然科学版)，2013(3)：344-347.

[4]陈长征，王刚，于慎波.低频时变时滞悬架系统的动态输出反馈鲁棒H_∞多目标控制[J].振动与冲击，2015，34(23)：153-160.

[5]王京祥，王在华.时滞状态反馈控制系统的稳定性增益区域[J].动力学与控制学报，2008，6(4)：15-20.

[6]陈龙祥，蔡国平.结构振动主动控制的多时滞控制律的设计方法[J].应用数学和力学，2009，30(11)：1318-1326.

Optimal Control of a Suspension System with Input Time-delay

DONG Tian-fu,FANG Ming-xia
(School ofAerospace Engineering andApplied Mechanics,Tongji University,Shanghai 200092,China)

With the application of active control suspension system,time-delay phenomena are inevitable in the automobile suspension system.Based on the time-delay,a 2-DOF active suspension system is studied.The traditional control law without considering the time-delay and the optimal control law with time-delay treatment through state transformation and system discretization methods are respectively applied to the system control.The control system responses and stability characteristics are compared.Theoretical analysis and numerical simulation show that when the delay value is small,the system remains stable.But,if it reaches a certain value,the system response characteristics may change qualitatively,even the system diverges and becomes instable.Using the state transition method to deal with the time lag can guarantee the stability of the active control system.The control law can reflect the influence of input delay on the governing equations pertinently.

vibration and wave;time-delay system;active suspension;optimal control;numerical calculation

U463.33

：A

：10.3969/j.issn.1006-1355.2017.04.003

1006-1355(2017)04-0011-04+24

2017-02-23

国家自然科学基金资助项目（11032009）；国家自然科学基金资助项目（51075303）

方明霞，女，博士生导师，主要研究方向为动力学与控制。

E-mail:92226@tongji.edu.cn

董天夫，男，硕士研究生。

E-mail:dongtianfu0805@sina.com