整体式与分布式双层隔振系统性能对比研究
2017-09-03周相荣
张 伟,周相荣,贺 华,丁 炜
(上海船舶设备研究所,上海 200031)
整体式与分布式双层隔振系统性能对比研究
张 伟,周相荣,贺 华,丁 炜
(上海船舶设备研究所,上海 200031)
为改善整体式双层隔振系统中间质量因实际工程空间尺寸、质量以及加工精度限制导致刚性相对弱、质量偏心大和弹性效应明显而引起的隔振效果降低问题,采用中间质量为分布式双层隔振系统是一种处理措施。本文通过偏心激励下的非对称双层隔振系统理论建模,对比研究在同等条件下整体式统和分布式双层隔振系统隔振效果。研究结果表明分布式双层隔振系统在中高频隔振效果明显优于整体式双层隔振系统,且在小于整体式质量比时仍能获得相当的隔振效果,对工程应用具有一定指导价值。
振动与波;双层隔振;分布式中间质量;偏心激励;非对称;隔振效果
双层隔振系统其实质是在单层隔振中再插入一个弹性支承的中间质量。在双层隔振的设计中,中间质量多采用整体框架式结构,以获得较大的质量和刚性[1]。当中间质量一定时,为保证框架刚性,结构尺寸一般较大。但在实际条件下,结构尺寸往往受到限制,中间框架刚性小,弹性效应增加,易导致系统隔振效果变差,而且大尺寸整体框架的转动惯量大,偏心时更不利于隔振。为解决此类问题,有专家学者提出分布式小中间质量块的双层隔振系统。文献[2]、[3]分别通过实验与理论研究说明分布式小中间质量块对隔振系统的影响,证明分布式质量块的可行性。文献[4]建立具有中间小质量块结构的对称隔振系统,研究其在单一激励下的功率流特性。文献[5]对比研究具有中间小质量块结构的隔振系统与柔性浮筏隔振系统的差异,得出小质量块结构可以抑制整体式筏架的弹性效应对中高频的影响。在以上的研究中,隔振系统都是建立在对称基础上的,而在工程实际中,由于受到安装条件以及设备自身偏心的影响,隔振系统往往是非对称的,同时系统激励力也存在偏心的现象[6]。
文中通过建立偏心激励下整体式和分布式中间质量的非对称双层隔振系统模型。在同等条件的情况下,利用导纳矩阵法,以力传递率为评价标准,研究对比两种隔振系统的隔振效果。
1 整体式与分布式双层隔振系统的建模
在工程中,由于受到设备加工误差、安装条件限制等多方面因素的影响,激励中心、刚度中心与质心存在不一致的情况。依照常见的设备建立如图1所示的双层隔振系统,其中图1(a)为整体式双层隔振系统,图1(b)为分布式双层隔振系统。
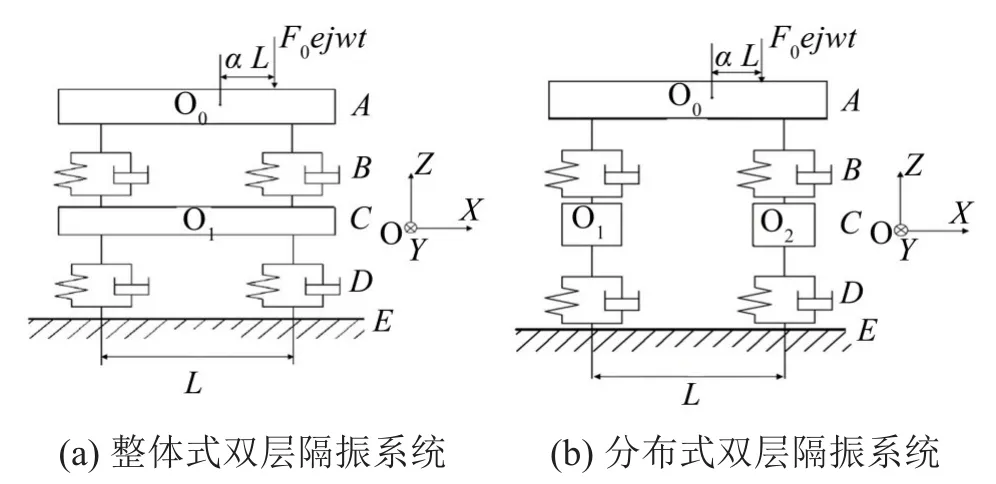
图1 双层隔振系统
图1所示为简化模型,假设设备关于oxz平面对称,则可将三维立体空间简化为二维平面。在oxz平面内,由于沿x方向的位移较小,在此忽略x方向振动的影响,隔振系统有沿z轴的垂向振动和绕y轴的转动。图中,将两种隔振系统都分为5个子系统,其中:子系统A(上部设备)视为存在一定偏心的刚体。令为设备质心的激励力矢量,其中F0为偏心简谐激励力的幅值;M0=F0αL为偏心力矩;为质心处的速度矢量。FAO=为子系统A的输出力矢量;为子系统A的输出速度矢量。
子系统B(上层隔振器)视为简单的弹簧阻尼系统,忽略质量,具有一定的扭转刚度。


2 整体式与分布式双层隔振子系统分析
2.1 设备子系统
图2所示为简化的设备子系统示意图。根据动力学分析可知

图2 设备子系统

将其改写成矩阵形式,即

由速度矢量间的转化关系可知

式(3)中R0=T0T。
根据式(1)至式(3),可将其改写为导纳矩阵的形式

式(4)中A11=G-10;A12=G-10T0;A21=R0G-10;A22=R0G-10T0。
2.2 上、下层隔振器子系统
上层选取规格相同的隔振器,根据隔振器的四端参数可知[7]

式(5)中i=1,2分别表示左、右两个隔振器的四端参数;I为2×2阶单位矩阵。
根据式(5)可以写出上层隔振器子系统的四端参数为

式(6)中

下层隔振器子系统四段参数与上层隔振器子系统相似,此处不做赘述。
2.3 中间质量子系统
2.3.1 整体式中间质量
图3为简化的整体式中间质量子系统示意图。将其视为刚体结构,根据动力学分析可知

图3 整体式中间质量子系统
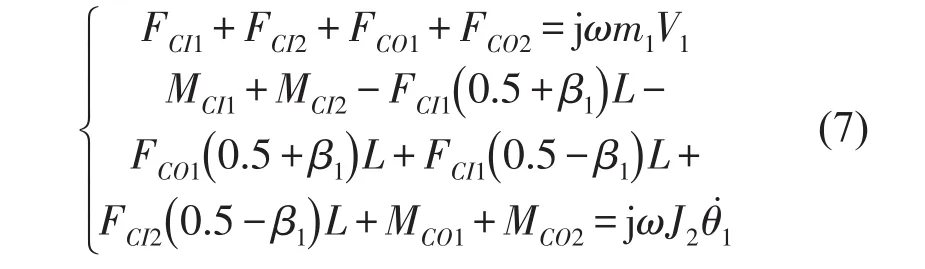
将其改写成矩阵形式,即

由速度矢量间的转化关系可知

式中R1=T1T。
根据式(7)-式(9)可将其改写为导纳矩阵的形式

2.3.2 分布式中间质量
图4为简化的分布式中间质量子系统示意图。根据动力学分析可知

将其改写成矩阵形式,即


图4 分布式中间质量子系统
由速度矢量间的转化关系可知

式中Ri=T1iT。
根据式(11)-式(13)可将其改写为导纳矩阵的形式
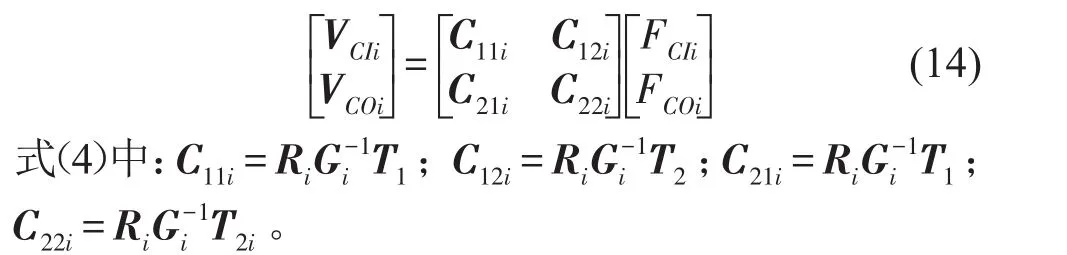
由式(14)可得分布质量块子系统的导纳矩阵为

2.4 基础子系统
基础子系统简化为刚度无穷大的刚性物体,因此基础上的速度矢量为零。
2.5 系统综合分析
由式(4)、式(6)、式(10)、式(15)以及子系统间的转化关系可得两种系统的导纳矩阵为

由式(18)可以看出整体式和分布式的区别主要在于子系统C的导纳矩阵的不同。
由于基础为刚性基础,则VE=0,由此可得

根据式(17)可知,两个系统的力与力矩传递率为

3 整体式与分布式双层隔振系统数值仿真与对比
两种系统的基本参数如表1所示。利用表中的数据对整体式与分布式双层隔振系统进行数值仿真并对比。
图5所示为对称系统受到质心力作用下下,两种隔振系统的力传递率图像对比。取整体式和分布式系统的质量比都为0.4。由图像可以看出,两种系统的力传递率完全相同,由于不存在力矩作用,则不存在力矩传递率。在非偏心激励作用下,两种系统都只有垂向的刚体模态被激发出来,其垂向振动固有频率为5.90 Hz、18.32 Hz。
图6所示为同等条件下偏心激励作用的非对称系统的传递率。其中图6(a)为力传递率,图6(b)为力矩传递率。仿真参数如表1所示,在工程实际中,由于隔振器的扭转刚度较小,在此分别取上下层隔振器的10%;整体框架结构的中间质量其尺寸较大,此处取10%的隔振器间距(即整体式中间质量偏心β1=0.1),而分布质量块的结构尺寸较小且加工误差小,此取2%的隔振器间距(即分布式中间质量偏心β2=0.02)。由图6(a),图6(b)看出,由于受到偏心激励及隔振系统偏心的影响,整体式与分布式的所有刚体模态都被激发出来,其中整体式隔振系统表现为4个共振峰值;分布式隔振系统表现为6个共振峰值。根据表中的数据和仿真结果可知:整体式双层隔振系统垂向频率为5.75 Hz和17.84 Hz,摇摆频率为13.23 Hz和39.80 Hz。分布式双层隔振系统垂向频率为 5.75 Hz、18.00 Hz,摇摆频率为 9.72 Hz、24.21 Hz、31.21 Hz、32.01 Hz。对比全对称系统和分布式与整体式系统可看出,非对称性使得两系统的垂向振动频率都向前移动,且整体式与分布式系统2阶垂向频率的偏移量并不一致,分布式系统的1阶扭转频率向前偏移较大。在低频阶段,分布系统的隔振效果与整体系统比较接近;而在中高频阶段,分布式系统的力传递率与力矩传递率效果优于整体系统。从图中截取的100 Hz~1 000 Hz频段内的数据可以看出:分布系统力传递率大致优于整体系统9dB~10 dB左右,力矩传递率大致优于整体系统2 dB~3 dB左右。

表1 两种系统的基本参数

图5 全对称系统
图7所示为减小分布系统质量比的传递率图像。在保持其他参数不变的条件下,取分布系统质量比为 0.5(m1=m2=25 kg)、0.45(m1=m2=22.5 kg),整体系统质量比不变(为0.6)。从图中可以看出,在减小分布系统质量比的情况下,高频阶段的隔振效果也优于或相当于整体系统的隔振效果。

图6 偏心非对称系统

图7 减小分布系统质量比
4 结语
通过以上的分析和数值仿真可以得到以下结论:
(1)在对称系统中,整体系统与分布系统的隔振效果一致;在偏心非对称系统中,分布系统在中高频的隔振效果较好。
(2)保持其他变量不变,仅降低分布系统中间质量比时,分布系统在中高频的隔振效果也明显好于整体系统。且在分布系统的中间质量比大于整体系统的75%时,隔振效果相当。质量比的降低体现较好的工程价值。
上述研究结果是在中间质量为刚性的基础上得出的,忽略了隔振器质量效应、中间质量弹性影响等,这些在以后将进行进一步研究,还将对隔振器的刚度、位置以及质量块个数进行优化设计。
[1]何琳,徐伟.舰船隔振装置技术及其进展[J].声学学报,2013,38(2):129-130.
[2]王光,董邦宜.小中间质量双层隔振试验研究[J].噪声与振动控制,1989,5(4):38-43.
[3]王孚懋,宋孔杰.小中间质量对复杂系统隔振效果的影响及最优设计[J].振动工程学报,1991,4(3):11-17.
[4]张树生,张克国,宋孔杰,等.具有中间质量结构振动功率流的传递特性[J].山东大学学报(工学版),2004,34(1):35-43.
[5]杨明月.分布参数双层隔振系统的主动控制机理研究[D].济南:山东大学.
[6]SONG KONG JIE,JIN LIN,HUO RUI,et al.Power flow transmission of an asymmetrical flexible system excited by an off-centre force[J].Chinese Journal of Mechanical Engineering,1999,12(3):183-184.
[7]严济宽.机械振动隔离技术[M].上海:上海科学技术文献出版社,1985:328-364.
Comparative Study on the Vibration Isolation Performance between the Entirety Double-layer and Distributed Double-layer Vibration Isolation Systems
ZHANG Wei,ZHOU Xiang-Rong,HE Hua,DING Wei
(Shanghai Marine Equipment Research Institute,Shanghai 200031,China)
In entirety double-layer vibration isolation systems,the intermediate mass block has relatively low rigidity and obvious flexible effect due to the limitation of space,mass and processing accuracy,which will reduce the vibration isolation effect of the systems.Using distributed intermediate-mass is an effective method to solve this problem.In this paper,the model of an asymmetric double-layer vibration isolation system subjected to eccentric excitation forces is built.The vibration isolation efficiencies of the entirety double-layer vibration isolation system and the distributed double-layer vibration isolation system in the same excitation conditions are studied respectively.The results show that the distributed asymmetric double-layer vibration isolation system has a better vibration isolation effect than the entirety asymmetric doublelayer vibration isolation system in the high frequency range.And it still has a good isolation effect when its mass ratio is less than that of the entirety double-layer isolation system.This study has a reference significance for engineering application.
vibration and wave;double-layer vibration isolation;distributed intermediate mass;eccentric excitation;asymmetric;vibration isolation efficiency
TH113.1
:A
:10.3969/j.issn.1006-1355.2017.04.006
1006-1355(2017)04-0025-05
2017-01-06
张伟(1992-),男,陕西省汉中市人,硕士生,主要研究方向为机械设备振动、噪声、冲击。
周相荣,男,研究员。
E-mail:zhouzxr@163.com
