一种高阻尼螺旋桨在宽带激励力下的振动特性研究

许慧春，郭云松，谌 勇，2，陈 锋，2，华宏星，2

（1.上海交通大学 机械系统与振动国家重点实验室，上海 200240；2.高新船舶与深海开发装备协同创新中心，上海 200240；3.中国船舶重工集团公司第七O四研究所，上海 200031）

一种高阻尼螺旋桨在宽带激励力下的振动特性研究

许慧春1，郭云松3，谌 勇1，2，陈 锋1，2，华宏星1，2

（1.上海交通大学 机械系统与振动国家重点实验室，上海 200240；2.高新船舶与深海开发装备协同创新中心，上海 200240；3.中国船舶重工集团公司第七O四研究所，上海 200031）

提出一种新型高阻尼螺旋桨结构形式，通过将螺旋桨桨叶简化为弯曲梁，对常规桨叶和新型桨叶的随机振动特性进行对比分析。首先利用基于均匀湍流统计模型的相关分析方法，求取了作用在桨叶表面上的压力谱空间分布；然后运用基于模态叠加法的随机振动理论，讨论了系统参数对桨叶叶尖速度响应功率谱和脉动推力功率谱的影响规律。研究表明新型螺旋桨结构形式具有降低叶片固有频率处峰值响应的效果。

振动与波；螺旋桨；弯曲梁；湍流；模态叠加法；随机振动

螺旋桨诱导的脉动推力是潜艇低频振动噪声的重要来源之一[1]。由于轴系纵向刚度大，螺旋桨在非定常艉流中运转时，其产生的脉动推力会通过轴系传递到艇体并引起艇体的振动和声辐射[2]。一般而言，螺旋桨脉动推力包含周期分量和宽频分量[3–4]。窄带周期分量主要来源于由鳍、舵等附体引起的空间非均匀流速艉流激励，通常出现在叶频及其倍频上[5–6]。宽频激励则分布在几赫兹到数百赫兹的范围内，且通常会在1阶叶频附近出现峰值[7–9]。其中，低频宽带力产生的原因主要是桨叶与进流中的湍流相互作用。螺旋桨进流中的湍流主要由船体及附体的边界层产生，并叠加了来流中的环境自由湍流，所以具有不同的特征积分尺度。为减小由螺旋桨激励力引起的艇体振动及辐射噪声，可采用不同的主动或被动控制措施，譬如早期采用的液压形式Michell轴承，以及国内近年来研制的纵振减振器等，对于被动措施的理论分析及优化讨论可参见文献[10–11]。另外还有在Leiws的基础上开展的主动及半主动措施研究等[12]。这些研究均以常规螺旋桨为研究对象，如图1(a)所示，且均假设螺旋桨是刚性桨，主要通过在轴系、轴承或基座上布置不同形式的隔振或吸振装置以控制纵向激励力。近几年的实船测试及诸多理论分析表明，实尺度的螺旋桨叶片固有频率可低至数十赫兹，会落在宽频激励能量比较集中的区域，由此引起的脉动推力放大作用不可忽视，同时研究表明提高螺旋桨阻尼能够有效降低螺旋桨的振动噪声。

因此，文中提出一种区别于常规螺旋桨的新型高阻尼螺旋桨的结构形式，如图1(b)所示，并在此基础上对影响桨叶振动噪声及脉动推力传递的主要系统参数进行参数化分析，为进一步的控制研究提供理论支撑。

1 理论方法

螺旋桨桨叶具有不规则的几何形状，为建立其微分方程，将其简化为Euler弯曲梁，忽略其扭转模态。常规螺旋桨和新型螺旋桨的结构形式示意图如图1所示。对于图1(a)所示的常规螺旋桨，将其单根桨叶简化为如图1(c)所示的悬臂梁，对于图1(b)所示的新型螺旋桨，将其单根桨叶简化为如图1(d)所示的桨叶中间靠根部处简支、根部连接阻尼器的梁。其中，L1为新型桨叶在桨毂内段的长度，L2为新型桨叶在桨毂外段的长度，L2与常规桨叶长度L相等。

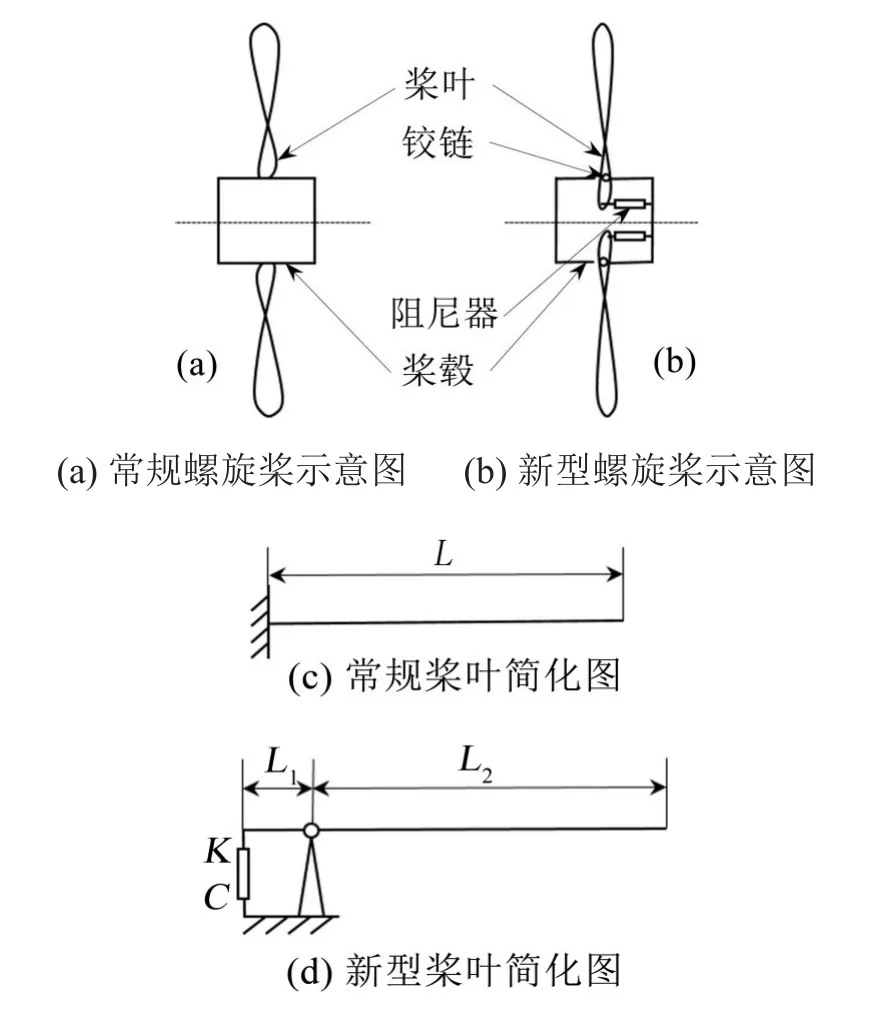
图1 常规螺旋桨和新型螺旋桨的结构形式示意图

采用两步法计算湍流进流诱发的桨叶弹性响应问题。第一步，利用均匀湍流统计模型，采用基于条带的相关分析方法，求取螺旋桨叶片上每一条带自身的功率谱及其与其他条带间的互功率谱矩阵，作为常规螺旋桨和新型螺旋桨两种方案共同的基本输入条件；第二步，利用基于模态叠加法的随机振动理论，通过参数化方法研究系统参数对桨叶速度响应功率谱和脉动推力功率谱的影响规律，并对两种方案的动态特性进行对比分析，验证在振动噪声抑制方面新型螺旋桨结构形式相比常规螺旋桨结构形式所具有的独特性能，从而为这种新型螺旋桨的进一步研制提供基本的理论基础。

由声学原理可知，平均辐射声功率和振动速度幅值的平方成正比，声辐射越大，潜艇隐身性能越差，显然，桨叶在叶尖处振动速度幅值最大。另外，由桨叶诱导产生的脉动推力会通过轴系传递到艇体上，引起艇体振动和产生噪声。故着重研究这两种方案中桨叶叶尖的振动速度谱以及由桨叶诱导产生的脉动推力谱。

1.1 各向同性湍流条件下的非定常升力谱计算

运用基于条带理论的湍流相关分析方法[8]，以常规螺旋桨为研究对象，将每片螺旋桨叶划分为图2所示的40个条带，利用来流中湍流的时空相关特性及不同条带之间的几何关系，求取各条带自身及不同条带之间的力谱，将所求力谱作为常规桨叶和新型桨叶在1.3节中的输入。

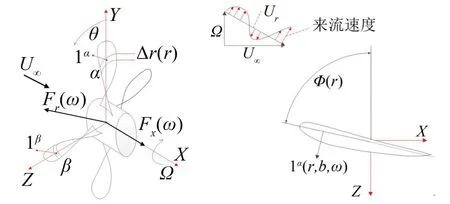
图2 湍流进流诱导的螺旋桨桨叶的升力脉动

以张量的形式描述时，上标代表不同的条带编号，x1、x2、x3、x4分别对应第α、β、γ、δ个条带中心到叶根的距离，下标代表不同的方向。譬如表示由第β个条带在j方向上在τ时刻作用在第α片条带上i方向t时刻的水动力。表示所有β单元上所有j方向以及所有τ时间流速脉动导致的α片条带上i方向t时刻的水动力

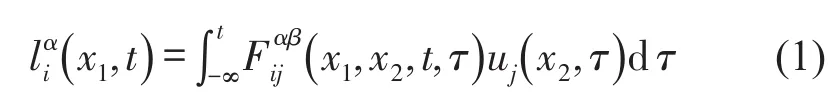
其中i,j=1,2,3,α,β=1,2,3,···,n

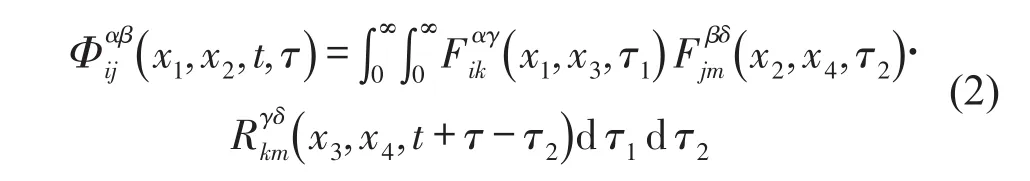
对式(2)进行傅里叶变换，则可得到不同条带之间的互谱函数

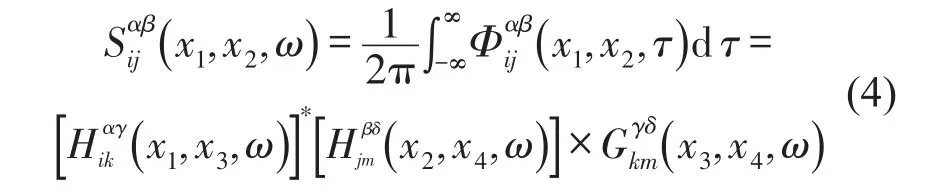
采用空间各向同性的湍流模型，该模型中两点的速度相关函数不随位置的迁移发生变化。通过该假设，任意两点的速度相关函数可以写成正则化的纵向和横向相关函数。另外，假设流场无散以及沿着流线指数衰减。为任意两点速度之间的相关函数，进而求得在不同频率处垂直于叶片表面的力谱矩阵表示垂直于桨叶表面的随机力，由于α、β与x1、x2一一对应，故在下文中将简记为

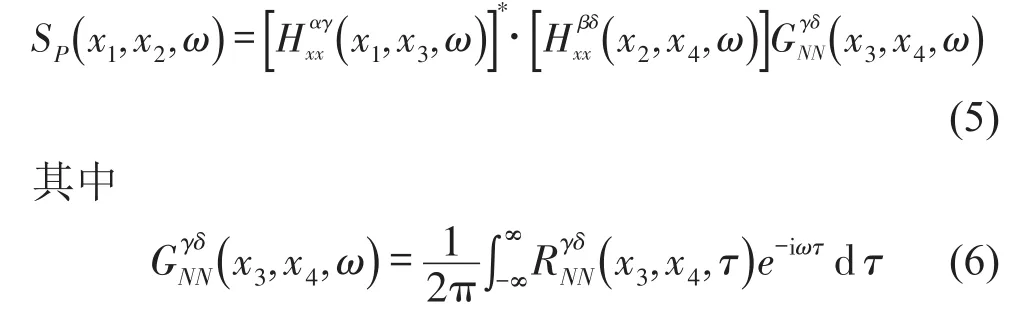
1.2 系统阻尼分析

系统各阶阻尼比ζi和系统各阶总损耗因子ηTi的线性关系如式(7)所示。各阶总损耗因子ηTi由机械损耗因子ηm、声辐射损耗因子γi、水动力损耗因子ηHi三部分构成，对系统的动态性能具有非常重要的影响。其中，声辐射损耗因子的影响相对其他两项较小[3]，故忽略声辐射损耗因子的影响。

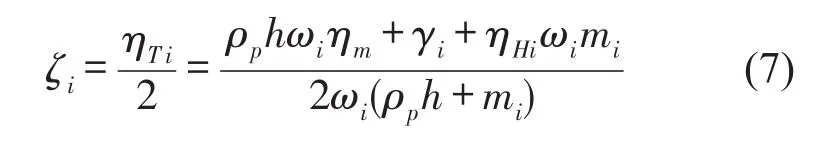
其中mi=ρ0(π/2)w(1+ωiw/c)-1，ωi为桨叶的各阶固有频率，w为桨叶宽度，c为海水中的声速，ρp为桨叶材料密度，ρ0为海水密度，h为桨叶等效厚度，i=1,2,3···。

常规桨叶机械损耗因子ηm取1%，表示桨叶自身机械结构阻尼；新型螺旋桨中阻尼器阻尼同样以机械损耗因子体现，ηm取1%表示忽略阻尼器阻尼，仅考虑桨叶自身机械结构阻尼,当ηm取3%、5%时，则表示考虑阻尼器阻尼的影响并令其逐渐增大。设潜艇前进速度U∞=4.62 m/s，螺旋桨转速Ω0=1.9 r/s，桨叶上任意一点的合成速度为U0(r)，根据式(8)求得等效合成速度

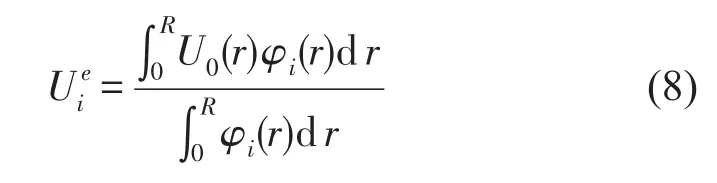
将式(8)、式(9)代入式(7)，即可求得系统各阶总损耗因子ηTi和系统各阶阻尼比ζi。

1.3 桨叶的随机响应分析

将两种方案中的桨叶均简化为Euler弯曲梁，假设桨叶表面的随机力p(x,t)是平稳过程，且在空间和时间上都具有零均值。前面已求出桨叶上均布的40个条带之间的随机力自谱和互谱矩阵Sp(x1,x2,ω)，作为常规螺旋桨和新型螺旋桨两种方案共同的基本输入条件。该分析方法对传统螺旋桨和新型螺旋桨均适用，区别仅仅在于振型函数和固有频率不同。

当考虑桨叶的内黏性阻尼c1时，Euler弯曲梁的振动微分方程表示为

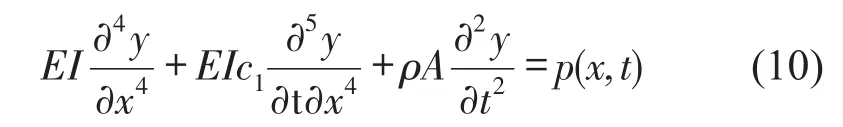
根据模态叠加法，式(10)的样本解可以表示为

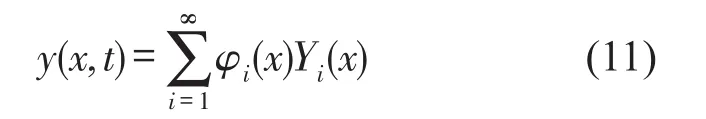
根据Euler梁的弯曲振动方程及其边界条件，通过Matlab编程分别求得两种方案中桨叶的固有频率ωi、对应的振型函数φi(x)和模态响应Yi(t)，从而可求得桨叶截面位移

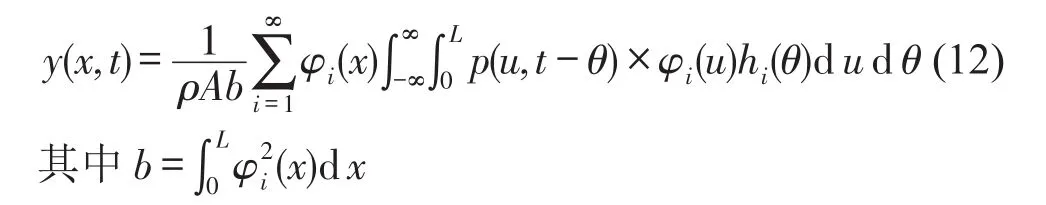
继而求得桨叶截面位移的协方差函数

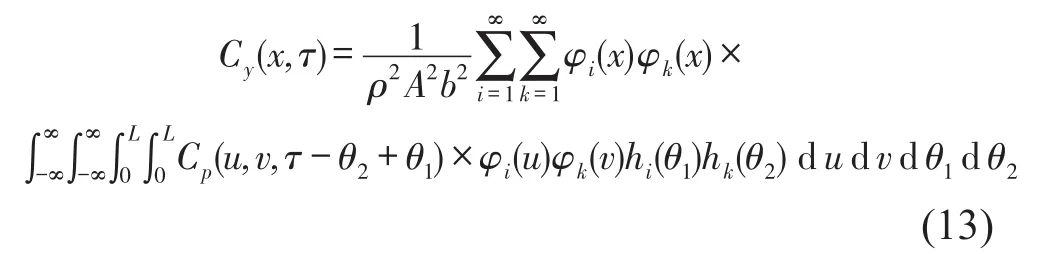
进而求得桨叶截面位移的功率谱为

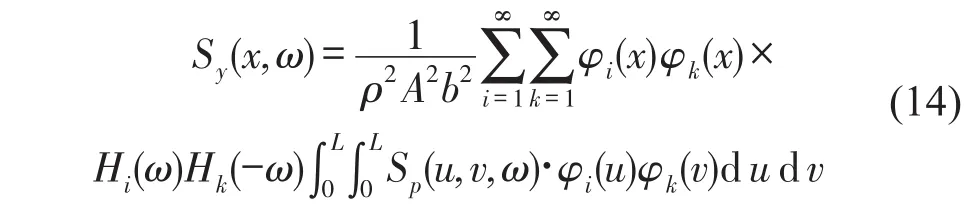
根据零均值平稳随机过程的性质，可得桨叶截面速度ẏ(x,t)的功率谱为

根据剪力公式可得桨叶截面剪力V(x,t)的功率谱为

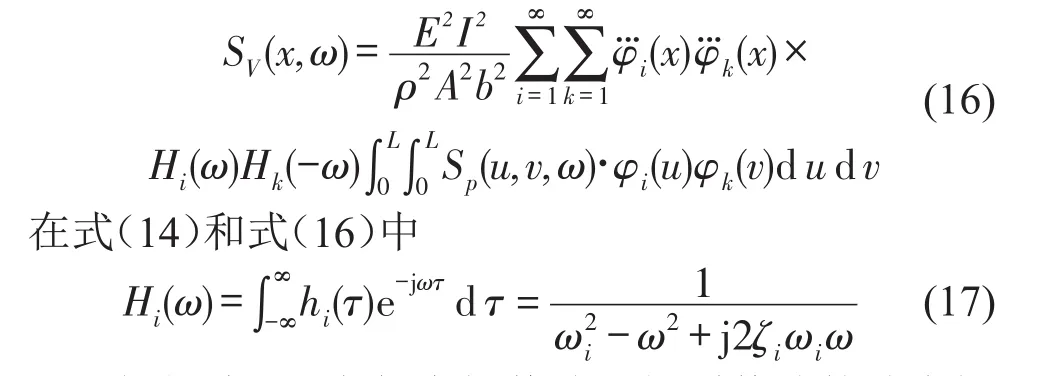
根据式(15)求得常规桨叶和新型桨叶的叶尖振动速度功率谱分别为Sv1(ω)和Sv2(ω)

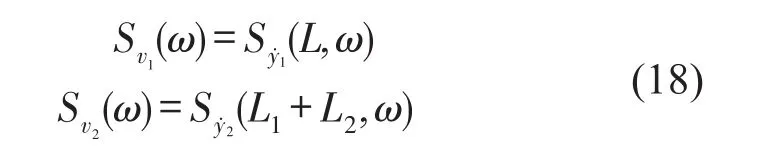
根据式(16)求得常规十叶螺旋桨和新型十叶螺旋桨传递到桨毂基础上的脉动推力功率谱分别为St1(ω)和St2(ω)，其中新型桨叶脉动推力由三部分组成，包括桨叶根部剪力SV2left(0,ω)、铰链左端剪力SV2left(L1,ω)和铰链右端剪力SV2right(L1,ω)。

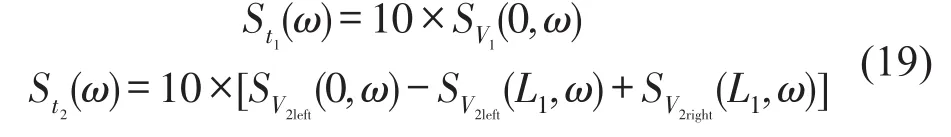
2 参数化研究及其对比分析

2.1 研究对象

以均匀布置的十叶桨为研究对象。该桨的尺寸基于70年代Sevik测试过的一个桨模[7]，固定弦长25.4 mm，无侧斜，方形叶梢，设计进速比为1.19。为降低其固有频率，对其进行缩尺比为5的几何放大。图3给出常规螺旋桨的几何外形和放大后的基本尺寸，两种桨叶的弹性模量E、桨叶等效密度ρ、桨叶截面面积A以及对Y轴的惯性矩I均相同，弹性模量E=4×104MPa；由于桨叶振动时会产生流体附连水质量，故桨叶等效密度大于其实际的材料密度，运用有限元软件Abaqus计算得到桨叶等效密度ρ=9.75×10-6kg/mm3；桨叶宽度w=286 mm；桨叶截面面积A=8 000 mm2；梁横截面对Y轴的惯性矩I=8.003×105mm4；常规桨叶长L=825.5 mm；新型桨叶桨毂外段叶长L2=L=825.5 mm，新型桨叶桨毂内段叶长L1通过L1/L2的比值e来调节。

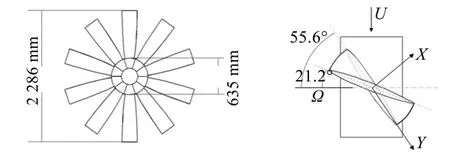
图3 十叶螺旋桨几何形状及尺寸

2.2 主要影响参数及评价指标

通过参数化方法讨论新型桨叶中阻尼器的刚度k、机械损耗因子ηm及桨毂内段叶长L1三项系统参数分别对两种方案中叶尖速度响应功率谱Sv1,2(ω)及由桨叶诱导产生的脉动推力功率谱St1,2(ω)两项评价指标的影响。其中，叶尖振动速度功率谱参考值取1(m∙s-1)2/(rad∙s-1)，脉动推力功率谱参考值取1 N2/(rad∙s-1)，求得两项评价指标的分贝值。

2.3 阻尼器刚度k对评价指标的影响

图4 螺旋桨阻尼器刚度k对评价指标的影响

两种方案均只考虑桨叶自身机械结构阻尼，忽略新方案中阻尼器阻尼，令两种方案中的机械损耗因子ηm均取1%，并保持比值e=1/4，改变新方案阻尼器刚度k，得出两种方案的随机响应特性见图4。新型桨叶中，各阶固有频率在刚度k的各个取值下均小于常规桨叶，刚度k主要影响系统固有频率，刚度越小各阶固有频率越低，曲线在低频处重合度较高，表明刚度对低频影响甚微，对高频影响显著；刚度对两项评价指标的各阶峰值均影响很小，当k=4×107N/m时，两项评价指标的第4阶峰值均明显小于k其他取值的情况及传统桨叶，但在0～600 Hz的频域范围内出现第5阶峰值，从而产生更多的共振点。故在实际应用中可通过选择适当的阻尼器刚度，使得系统各阶固有频率尽量错开激励的频率范围，从而避免因共振导致过大的声辐射和脉动推力。

2.4 机械损耗因子ηm对评价指标的影响

保持新型桨叶中阻尼器刚度k为2×108N/m，比值为e=1/4，通过其机械损耗因子来调整阻尼器阻尼，得出两种方案的随机响应特性见图5。常规桨叶和新型桨叶前4阶固有频率分别为16.6 Hz、104.3 Hz、291.9 Hz、572.0 Hz和 14.3 Hz、92.5 Hz、262.9 Hz、512.8 Hz，可见新型桨叶各阶固有频率比传统桨叶低。当两种方案的机械损耗因子ηm均取1%时，两项评价指标的各阶峰值均相差不大，甚至在第2、3阶固有频率处新方案略大于传统方案，这是由于新方案中忽略阻尼器阻尼后，阻尼器等效为无阻尼的弹簧，故新型桨叶较常规桨叶稍软，从而使得新型桨叶具有较低的固有频率和相对稍大的速度响应。随着新型桨叶机械损耗因子提高，两项评价指标各阶峰值均不同程度地减小，机械损耗因子越大，各阶峰值减小越多，说明阻尼越大，消耗越多的能量，而远离共振区时阻尼对两项评价指标的峰值影响不大。曲线在低频处重合度较高，表明机械损耗因子对两项评价指标的低频峰值影响甚微，对抑制高频峰值作用显著，阶数越高峰值减小越显著，表明在低频时机械损耗因子在系统阻尼中不起主导作用，由水动力损耗因子起主导作用；当频率提高时，水动力损耗因子在系统阻尼中的比重逐渐降低，同时机械损耗因子比重逐渐提高。在第3、4阶固有频率处新型桨叶两项评价指标峰值均明显小于常规桨叶。可以预见，当机械损耗因子继续提高时，新型桨叶的两项评价指标的各阶峰值还将得到进一步抑制，从而进一步减小螺旋桨的声辐射和传递到桨毂上的脉动推力。这表明新型桨叶比常规桨叶具有更好的减振降噪性能。

2.5 桨毂内段叶长L1对评价指标的影响

两种方案中桨叶机械损耗因子均取为1%，同时保持新方案中阻尼器刚度k=2×108N/m，通过调节比值e研究桨毂内段叶长L1对系统振动特性的影响，得出两种方案的随机响应特性见图6。由图6(a)可见，曲线在低频处重合度较高，表明e在低频处对固有频率和叶尖速度功率谱各阶峰值影响较小，在高频处对固有频率影响较大，e越大新型桨叶各阶固有频率越低，当e=1/3时，叶尖速度响应功率谱的第4阶峰值较e的其他取值以及常规桨叶的对应峰值更低，但在0～600 Hz频域内出现第5阶峰值，从而产生更多的共振点。由图6(b)可见，当e=1/5时，脉动推力功率谱在第1阶固有频率处相对常规桨有放大作用，在第3、4阶固有频率处相对常规桨则有明显的抑制作用。当e=1/4时，各阶峰值均与常规螺旋桨非常接近。当e=1/3时，脉动推力功率谱在第1阶固有频率处相对常规桨有放大作用，且放大作用较e=1/3弱，在第2、3阶固有频率处相对常规桨则有明显的抑制作用。故应根据e不同取值时的系统特性、工作环境、工作要求和桨毂内安装空间综合确定桨毂内段叶长L1的取值。

3 结语

基于湍流统计模型及随机振动理论，对常规螺旋桨和文中提出的新型高阻尼螺旋桨结构形式在均匀湍流进流作用下的随机响应进行分析对比，并研究新型螺旋桨中三个系统参数对叶尖振动速度响应功率谱和螺旋桨脉动推力功率谱的影响规律，通过计算分析可以得到以下结论：

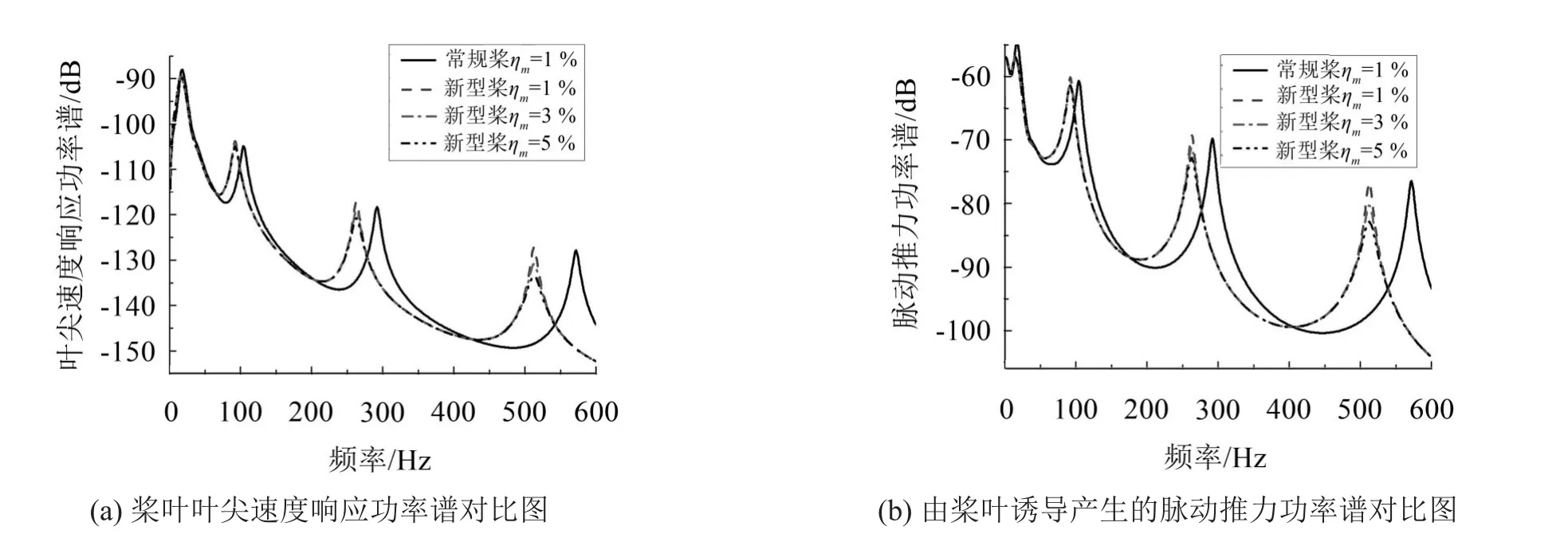
图5 机械损耗因子ηm对评价指标的影响

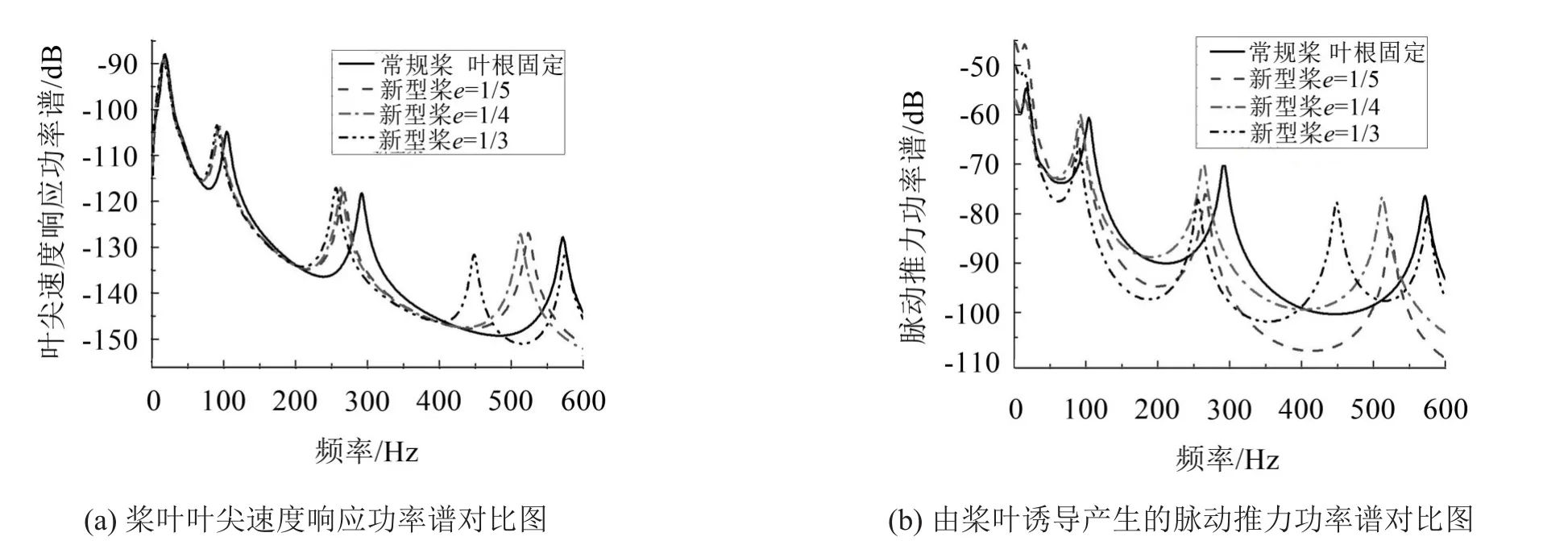
图6 比值e对评价指标的影响

（1）频率越低，水动力损耗因子在系统阻尼中比重越高，同时机械损耗因子比重越低。增加系统阻尼对于振动噪声控制是有利的，特别是增加桨叶的阻尼，既能降低纵向脉动力，也能降低桨叶自身的振动和声辐射，是控制螺旋桨宽频激励引起的振动噪声问题的理想途径之一。

（2）新型螺旋桨中阻尼器刚度主要影响系统固有频率，且对高频影响更为显著，刚度越小，各阶固有频率越低。实际应用中应根据激励力频段和工作要求选择适当的阻尼器刚度，使得系统固有频率尽量避开激励力频段，从而避免因共振而导致过大的声辐射和脉动推力。

（3）新型桨叶桨毂内段叶长L1对叶尖速度响应功率谱各阶峰值影响较小，对系统固有频率和脉动推力功率谱各阶峰值作用明显，L1越小，各阶固有频率越大。e的不同取值对应不同的系统特性。e在某些取值下，新型桨相对传统桨在低频处对脉动推力功率谱起放大作用，在高频处起抑制作用，如e=1/5时的情况。故应根据e不同取值时的系统特性、工作环境、工作要求和桨毂内安装空间综合确定桨毂内段叶长L1的取值，从而使得新型螺旋桨相对于常规螺旋桨达到降低桨叶振动速度谱和脉动推力谱的目的。

[1]ROSS D,KUPERMAN W A.Mechanics of Underwater Noise[J].The Journal of the Acoustical Society of America,1989,86(4):1626-1626.

[2]MERZ S,KINNS R,KESSISSOGLOU N.Structural and acoustic responses of a submarine hull due to propeller forces[J].Journal of Sound and Vibration,2009,325(1):266-286.

[3]BLAKE W K.Mechanics of flow-induced sound and vibration V2:Complex flow-structure interactions[M].Elsevier,2012.

[4]HOMICZ G F,GEORGE A R.Broadband and discrete frequency radiation from subsonic rotors[J].Journal of Sound and Vibration,1974,36(2):151-177.

[5]THOMPSON D E.Propeller time-dependent forces due to nonuniform flow[D].Pennsglvania State Univ.,University Park,1976.

[6]MASSARO M,GRAHAM J M R.The effect of threedimensionality on the aerodynamic admittance of thin sections in free stream turbulence[J].Journal of Fluids and Structures,2015,57:81-90.

[7]SEVIK M M.The response of a propulsor to random velocity fluctuations[R]. Pennsylvania State Univ.,University Park Ordnance Research Lab,1970.

[8]JIANG C W,CHANG M S,LIU Y N.The effect of turbulence ingestion on propeller broadband thrust[R].David TaylorResearch Center,BethesdaMd Ship Hydromechanics Dept,1991.

[9]YOUNG Y L.Fluid-structure interaction analysis of flexible composite marine propellers[J].Journalof Fluids and Structures,2008,24(6):799-818.

[10]DYLEJKO P G,KESSISSOGLOU N J,TSO Y,et al.Optimisation of a resonance changer to minimise the vibration transmission in marine vessels[J].Journal of Sound and Vibration,2007,300(1):101-116.

[11]MERZ S,KESSISSOGLOU N,KINNS R,et al.Minimisation of the sound power radiated by a submarine through optimisation of its resonance changer[J].Journal of Sound and Vibration,2010,329(8):980-993.

[12]LEWIS D W,ALLAIRE P E,THOMAS P W.Active magnetic control of oscillatory axial shaft vibrations in ship shaft transmission systems part 1:System natural frequencies and laboratory scale model[J].Tribology Transactions,1989,32(2):170-178.

Vibration Characteristics of a High-damping Propeller Subjected to Broadband Excitation Forces

XU Hui-chun1,GUO Yun-song3,CHEN Yong1,2,CHEN Feng1,2,HUA Hong-xing1,2
(1.State Key Laboratory of Mechanical System and Vibration,Shanghai Jiaotong University,Shanghai 200240,China;2.Collaborative Innovation Center forAdvanced Ship and Deep-Sea Exploration(CISSE),Shanghai 200240,China;3.704 Institute of CSIC,Shanghai 200031,China)

A new type of high-damping propeller structures is proposed.By simplifying the blade of the propeller into a cantilever beam,the random vibration characteristics of the blades of the new-type propeller and the traditional propeller are analyzed and compared.First of all,using the correlation method based on the statistical characteristics of isotropic turbulence,the pressure spectrum acted on the propeller surface is computed.Then,by using the random vibration theory based on modal superposition method,the influence of system parameters on the power spectral density of blades’velocity response and the unsteady force transmitted to the hull are discussed.It is shown that the new type of propeller structures can reduce the peak responses at the natural frequencies of the blades.

vibration and wave;propeller;cantilever beam;turbulence;modal superposition method;random vibration

U664.33

：A

：10.3969/j.issn.1006-1355.2017.04.002

1006-1355(2017)04-0005-06

2016-11-19

许慧春(1992－)，男，江苏省盐城市人，硕士生，主要研究方向为振动控制。

E-mail:xhcdhu@163.com

谌勇，男，研究员，博士生导师。

E-mail:chenyong@sjtu.edu.cn