城市轨道交通高架U型梁车-轨-桥耦合振动分析

汪振国，雷晓燕，罗 锟，徐 平

（1.华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013；2.北京交通大学 土木建筑工程学院，北京 100044）

城市轨道交通高架U型梁车-轨-桥耦合振动分析

汪振国1，雷晓燕1，罗 锟1，徐 平2

（1.华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013；2.北京交通大学 土木建筑工程学院，北京 100044）

基于多体动力学原理与有限元法，利用多体动力学软件Simpack建立三维车-轨-桥耦合振动仿真模型，对列车过桥时U型梁及轨道结构竖向和横向振动进行分析，研究扣件、板下弹性支承与桥梁支座参数对U型梁和轨道结构振动的影响，给出各参数合理取值范围。研究结果表明：列车以80 km/h的速度过桥时，1阶模态对U型梁局部振动贡献最大，且在轨道不平顺激励下，容易激发高阶模态，致使U型梁局部振动加剧；U型梁翼缘处横向振动不容忽视，且应重点关注钢轨与轨道板的竖向振动；增大扣件刚度可明显减小钢轨变形，但过大的扣件刚度会使轨道板和U梁振动加剧，建议扣件竖向刚度取值范围为20 MN/m～50 MN/m；增大板下弹性支承刚度可明显减小轨道板及钢轨的竖向变形，但过大的刚度将削弱轨道弹性，不利于减振，建议板下弹性支承竖向刚度取值范围为1.0×103MN/m～1.5×103MN/m；支座刚度在一定范围内增大可减小U梁、轨道板和钢轨的振动，但过大的刚度反而会使振动加剧，建议支座竖向刚度取值范围为3×103MN/m～4×103MN/m。

振动与波；耦合振动；U型梁；轨道结构；多体动力学

近年来，铁路轨道交通随着国民经济和人民生活水平的提高得到大力发展，具有重要的现实意义。在我国高速铁路和城市轨道交通中，高架桥梁结构应用极为普遍，京津城际高速铁路中桥梁占比高达87.7%，京沪高铁中桥梁占80.5%[1]。U型梁作为一种新型的城市轨道交通载体，与箱梁、T梁和板梁相比，具有建筑高度低、降噪效果好、环境噪声小、行车安全等诸多优点[2]，在城市轨道交通中应用日益广泛。然而高架桥梁所带来的结构振动噪声问题已成为制约城市轨道交通发展的重要因素。预应力混凝土桥梁结构振动会向四周辐射低频噪声（0～200 Hz），该频段噪声对人体身心健康能造成长期性危害[3–4]，因此，对城市轨道交通高架桥梁结构振动开展研究，找到减小桥梁结构振动的合理措施，对降低桥梁结构低频噪声、保障人体身心健康和促进轨道交通的发展都具有重要意义。

U型梁作为城市轨道交通的载体，列车通过U型梁桥时将会导致桥梁结构发生振动，同时，桥梁也会对车体产生反作用力，引起车辆振动[2]。这种车辆和桥梁之间的相互作用问题就是车桥耦合问题。一直以来，国内外学者围绕该问题开展了大量的研究工作，Tan等提出一种简化的车桥耦合模型并分析多参数对车桥耦合振动的影响[5]；Crockett等建立车辆-轨道-箱梁的有限元模型，并计算轮轨相互作用引起的结构振动[6]；Yang等采用动态缩聚法对车桥耦合系统求解方法进行改进，使得求解时的计算效率得以提高[7]；北京交通大学夏禾教授总结以往的研究成果，并结合理论创新，出版铁路车辆与桥梁结构相互作用的专著[8]；李奇等系统阐述利用有限元法对柔性车体车桥耦合系统的建模与分析方法[9]；崔圣爱等采用多体系统动力学理论与有限元法相结合的联合模拟技术进行车桥耦合振动仿真分析，为车桥耦合振动的研究提供了一种新型有效途径[10-11]。各学者依据研究目的、方向的不同，所采用的研究方法也各有差异，此外，以U型梁桥结构振动为对象的车桥耦合研究较少。

文中为研究列车过桥时桥梁及轨道结构的振动规律，基于多体系统动力学与有限元法，建立城市轨道交通U型梁桥的三维车轨桥耦合振动仿真模型，对列车过桥时U梁及轨道结构的竖向及横向振动进行研究，并探讨扣件、板下弹性支承与桥梁支座竖向刚度对U梁及轨道结构振动的影响，进而寻求各连接件参数的合理取值范围，从而为铁路高架桥梁结构的减振设计提供合理的参考。

1 模型建立

车轨桥耦合振动仿真模型以轮轨接触面为界，将模型分成上下两部分：上部为列车模型，将其考虑为多刚体系统，利用多体动力学软件Simpack建立；模型下部包括钢轨、轨道板、U型梁和桥墩，将上述结构部件均考虑为柔性体。

1.1 列车模型建立

参照地铁B型车基本参数建立车辆模型。列车模型由3辆车按两动一拖的形式进行编组，中间车辆为拖车，动车则位于两端，并通过车体间的钩缓装置实现编组挂接。为提高计算效率，依据本文研究目标，在计算模型中只考虑车辆的竖向和横向运动，不考虑纵向运动情况，因此单节车辆共选取27个自由度，如表1所示。计算中取列车速度为80 km/h，轨道不平顺按美国5级不平顺谱施加垂向（高低）和横向（方向）不平顺。

表1 单节车辆自由度

1.2 柔性体系统模型建立

轮轨接触面以下各结构部件均考虑为柔性体，应用有限元动力子结构技术单独对各部件进行处理，获得包含各部件的几何、质量、刚度、模态以及节点坐标信息文件，并通过Simpack接口程序，将上述信息文件转换成软件识别的*.fbi柔性体文件，以实现弹性结构模型转换为多体系统中柔性体结构模型。其中桥墩与大地固接，其它各结构间通过力元连接，共同构成多柔性体系统，如图1所示。

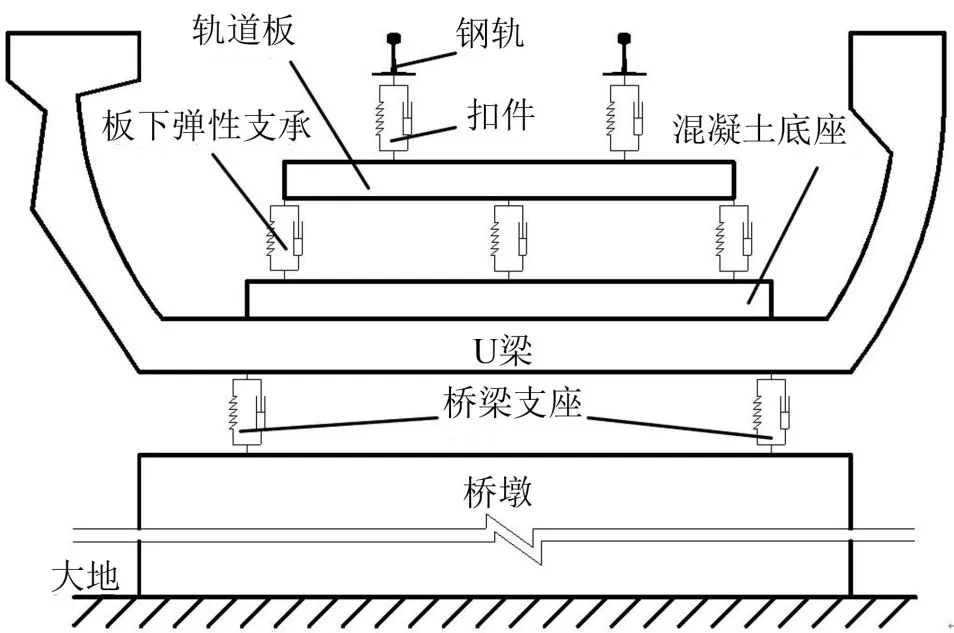
图1 柔性体系统

U型梁长30 m，混凝土底座浇筑于梁体底板之上，其截面尺寸为2 800 mm×200 mm（宽×高），混凝土底座与轨道板通过5号力元（Spring-Damper Parallel Cmp）连接，用以模拟板下弹性支承结构；轨道板截面尺寸为2 400 mm×190 mm（宽×高），其与钢轨同样使用5号力元连接，用以模拟扣件；钢轨采用60 kg/m钢轨，为提高计算效率，多体系统中只在桥梁段将其考虑为柔性体，桥梁范围外的钢轨考虑为刚体，多体系统中钢轨柔性体的实现除了需要上文所述的*.fbi文件外，还需自编*.ftr文件，该文件包含钢轨的长度、位置、轮轨接触面上钢轨离散点、节点误差、钢轨刚柔过度处理等信息，用以实现列车轮对与钢轨间的数据交互；桥墩通过5号力元连接于U梁底板之下，用以模拟桥梁支座。各结构及连接部件计算参数见表2、表3。

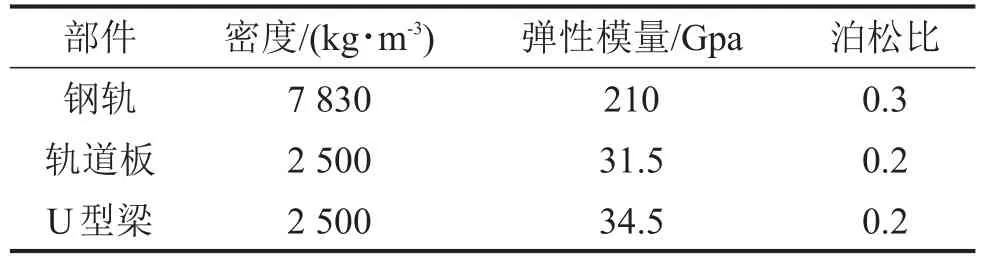
表2 结构部件计算参数

表3 连接部件计算参数

1.3 轮轨接触关系

在Simpack软件环境下，上部列车多刚体系统与下部柔性体系统通过轮轨接触关系实现耦合。采用78号力元（Rail-Wheel interface）模拟轮轨接触模型，如图2所示。

图2 轮轨接触图示

竖向轮轨力计算采用线性化赫兹接触理论；横向轮轨力计算是建立在赫兹接触理论基础之上，并使用Kalker滚动接触的非线性简化理论Fastsim算法[12]。

当列车过桥时，在轨道不平顺的激励下，上部列车动载将通过轮轨接触点作用于下部柔体系统上，从而诱发桥梁及轨道结构振动。桥梁结构振动属于低频振动，因此分析的频域范围选为0～200 Hz，仿真计算时积分步长取为0.002 s。车轨桥耦合振动仿真模型如图3所示。

图3 仿真计算模型

2 轨道结构及U型梁振动响应分析

基于建立的车轨桥耦合振动仿真模型，采用上文给出的计算参数，对单跨U型高架桥梁及轨道结构的竖向及横向振动响应情况进行分析，为研究桥梁整体的振动响应，在桥梁跨中、四分之一及支座截面处分别选取7个观测点，以桥梁跨中截面为例，如图4所示。

图4 跨中截面观测点布置

在桥梁翼缘、腹板、底板、轨道板及钢轨顶面设置7个观测点。振动响应最大值计算结果见表4。

表4 振动响应计算结果

针对U型梁结构振动，选取竖向振动最剧烈的跨中底板处以及横向振动最剧烈的支座截面右侧翼缘处作为特征点位，将其加速度时程数据转换为频域数据，对两者加速度进行频域分析，如图5、图6所示。

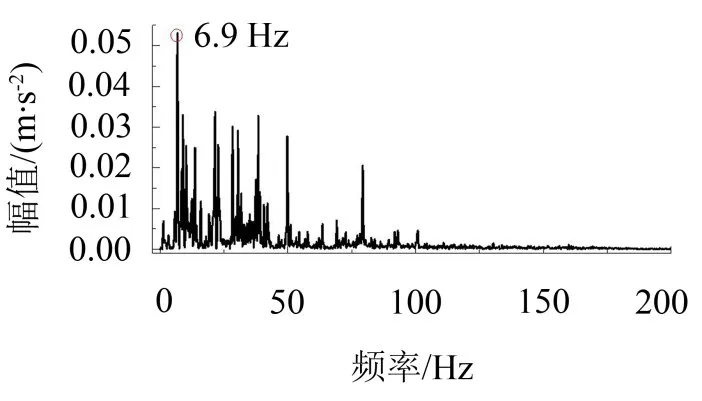
图5 竖向加速度频谱曲线

图6 横向加速度频谱曲线

由图5、图6可知：U梁加速度响应主要集中在100 Hz以下的范围内；竖向与横向加速度都在6.9 Hz达到最大值，而U梁模态基频为6.595 Hz，表明1阶模态对U梁局部振动贡献最大，U梁减振设计时应尽量避免基频的影响；除此之外，跨中底板竖向加速度在21.6 Hz、30.4 Hz、38.4 Hz、49.8 Hz及79.3 Hz时幅值较大，支座截面翼缘处横向加速度在30.4 Hz时幅值接近最大值，值得注意的是，在上述频率附近均有模态与之对应，表明在轨道不平顺的激励下，列车以80 km/h过桥时容易激发高阶模态，致使U梁振动加剧。U梁自振频率见表5。

3 参数影响分析

为研究扣件、板下弹性支承及桥梁支座竖向刚度对U梁及轨道结构振动的影响，选择跨中截面3号（U梁）、6号（轨道板）和7号（钢轨）观测点为参考点，通过分析得到各参考点改变连接结构竖向刚度值后的振动响应规律，进而寻求各连接结构竖向刚度的合理取值范围。

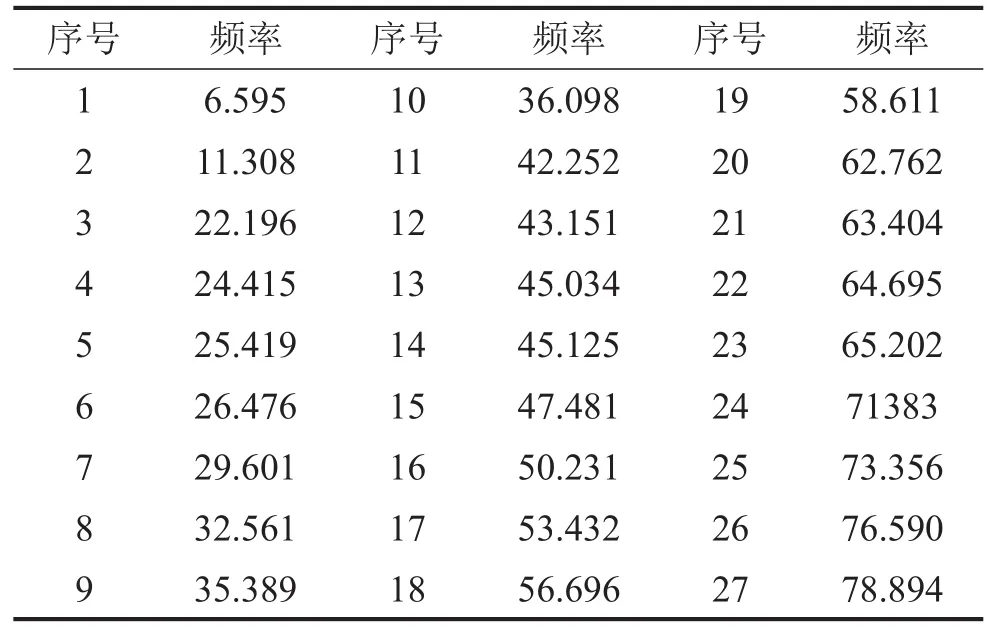
表5 U型梁自振频率/Hz

3.1 扣件竖向刚度影响分析

钢轨扣件是轨道上用以连接钢轨和轨下结构的重要中间连接件。轨道结构中使用的扣件形式多样，其刚度值也相差较大，例如科隆蛋扣件节点刚度为10 MN/m，而弹条Ⅲ型扣件节点刚度却达到60 MN/m[13]。固定其它计算参数，只改变扣件竖向刚度值，得到的各观测点竖向位移及竖向加速度最大值见表6。

由表6可知：扣件竖向刚度变化对U梁和轨道板的竖向位移影响很小，但两者加速度随刚度值增加而增加，且当刚度小于20 MN/m及大于60 MN/m时，加速度变化剧烈，如图7（a）所示；扣件竖向刚度变化对钢轨竖向加速度影响较小，但其竖向位移随刚度增加而减小，当刚度达到20 MN/m之后，减小趋势变缓，如图7（b）所示。由此可见，增大扣件刚度值可明显减小钢轨变形，但过大的扣件刚度会使轨道板和U梁竖向振动加速度急剧增加，建议高架U梁桥板式轨道较合理的扣件竖向刚度取值范围为20 MN/m～50 MN/m。

表6 扣件竖向刚度影响

3.2 板下弹性支承竖向刚度影响分析

为研究板下弹性支承竖向刚度对U梁及轨道结构振动的影响，选取9种不同刚度的板下支承结构进行对比分析，得到的各观测点竖向位移及加速度最大值列于表7。

由表7可知：改变板下弹性支承竖向刚度对U梁竖向位移、加速度及钢轨加速度影响不大；板下弹性支承竖向刚度增大，轨道板及钢轨竖向位移随之减小，如图8所示，轨道板竖向加速度先减小，当刚度达到1.5×103MN/m后呈增大趋势。由此可见，增大板下弹性支承刚度可明显减小轨道板及钢轨的竖向变形，但过大的刚度对提高轨道弹性、减缓振动不利，建议高架U梁桥板式轨道较合理的板下弹性支承竖向刚度取值范围为1.0×103MN/m～1.5×103MN/m。

图7 扣件竖向刚度变化影响

图8 弹性支承竖向刚度变化影响

表7 板下弹性支承竖向刚度影响

表8 桥梁支座竖向刚度影响

3.3 桥梁支座竖向刚度影响分析

为研究不同桥梁支座竖向刚度对U梁及轨道结构振动的影响，参考常用的几种桥梁支座刚度，选取6种不同刚度的支座进行对比分析，得到的各观测点竖向位移及加速度最大值见表8。

由表8可知：U梁和轨道板的竖向位移、加速度以及钢轨竖向位移随刚度增大先减小，当刚度达到5×103MN/m后，呈增大趋势；钢轨加速度受支座刚度变化不大。由此可见，支座刚度在一定范围内增大可减小U梁、轨道板和钢轨的振动，过大的刚度反而会使振动加剧，建议高架U梁桥支座竖向刚度较合理的取值范围为3×103MN/m～4×103MN/m。

4 结语

基于多体系统动力学与有限元法，建立了城市轨道交通U型梁桥的列车-轨道-桥梁-桥墩三维车轨桥耦合振动仿真模型，对列车过桥时的U梁及轨道结构竖向和横向振动情况进行分析，并探讨各连接结构竖向刚度对U梁和轨道结构的影响，得到以下几点结论：

（1）U型梁横向振动不容忽视，尤其应注意翼缘处横向振动情况；钢轨与轨道板横向位移较小，但竖向位移变化剧烈，应注意钢轨与轨道板的竖向振动情况。

（2）列车以80 km/h的速度过桥时，1阶模态对U梁局部振动贡献最大，U梁减振设计时应尽量避免基频的影响；在轨道不平顺的激励下，列车过桥时容易激发高阶模态，致使桥梁局部振动加剧。

（3）增大扣件刚度可明显减少钢轨变形，但过大的扣件刚度会使轨道板和U梁振动加速度急剧增加，建议扣件竖向刚度取值范围为20 MN/m～50 MN/m；增大板下弹性支承刚度可明显减小轨道板及钢轨的竖向变形，但过大的刚度对提高轨道弹性、减缓振动不利，建议板下弹性支承竖向刚度取值范围为1.0×103MN/m～1.5×103MN/m；支座刚度在一定范围内增大可减小U梁、轨道板和钢轨的振动，但过大的刚度反而会使振动加剧，建议支座竖向刚度取值范围为3×103MN/m～4×103MN/m。

（4）文中只研究了单跨U型梁桥的结构振动，对于多跨或者其它梁型的桥梁结构振动问题还有待进一步研究。

[1]罗锟，雷晓燕，曾少辉.无砟轨道-箱梁结构振动传递及参数影响分析[J].噪声与振动控制，2016(6)：126-130.

[2]王彬力，蒲黔辉，白光亮.新型U型梁车桥耦合环境振动实测与分析[J].地震工程与工程振动，2012，32(1)：78-85.

[3]THOMPSON D J,JONES C J C.A review of the modelling of wheel/rail noise generation[J].Journal of Sound&Vibration,2000,231(3):519-536.

[4]WAYE K P.Effects of low frequency noise and vibrations:environmental and occupational perspectives[A]//Nriagu J O.Encgclopedia of Environmental Health[M].Burlington,2011:240-253.

[5]TAN G H,BRAMELD G H,THAMBIRATNAM D P.Development of an analytical model for treating bridgevehicle interaction[J].Engineering Structures,1998,20(1-2):54-61.

[6]CROCKETT A R,PYKE J R.Viaduct design for minimization of direct and structure-radiated train noise[J].Journal of Sound&Vibration,2000,231(3):883-897.

[7]YANG Y B,LIN B H.Vehicle-bridge interaction analysis by dynamic condensation method[J].Journalof Structural Engineering,1995,121(11):1636-1643.

[8]夏禾.车辆与结构动力相互作用[M].北京：科学出版社，2002.

[9]李奇，吴定俊，邵长宇.考虑车体柔性的车桥耦合系统建模与分析方法[J].振动工程学报，2011，24(1)：41-47.

[10]崔圣爱，祝兵.客运专线大跨连续梁桥车桥耦合振动仿真分析[J].西南交通大学学报，2009，44(1)：66-71.

[11]崔圣爱，祝兵，黄志堂.基于多体系统动力学和有限元法的联合仿真在车桥耦合振动研究中的应用[J].计算机应用研究，2009，26(12)：4581-4584.

[12]KALKER J.J.A fast algorithm for the simplified theory of rolling contact[J].Vehicle System Dynamics,1982,11(1):1-13.

[13]王其昌.无碴轨道钢轨扣件[M].成都：西南交通大学出版社，2006.

Analysis of Vehicle-Track-Bridge Coupling Vibration for the U-shaped Girder in Urban Rail Transit

WANG Zhen-guo1,LEI Xiao-yan1,LUO Kun1,XU Ping2
(1.Engineering Research Center of Railway Environment Vibration and Noise,Ministry of Education,East China Jiaotong University,Nanchang 330013,China;2.Department of Civil and Architecture Engineering,Beijing Jiaotong University,Beijing 100044,China)

A three-dimensional model for vehicle-track-bridge coupling vibration simulation is established by Simpack code based on multi-body dynamics and finite element method.The vertical and lateral vibration of the U-shaped girder and track structure is analyzed when the train is traveling through the bridge.The influence of parameters of fasteners,elastic supports under the track plate and the supports of the girder on the vibrations of the U-shaped girder and the railroad structure is analyzed.And the reasonable range of each parameter is presented.The results show that when the train is traveling through the bridge at 80 km/h speed,the first order mode has the largest contribution to the local vibration of the U-girder.Under the excitation of track irregularity,the higher order mode can be stimulated readily so that the local vibration of the U-girder aggravates.The lateral vibration at the flange of the girder cannot be ignored,and the vertical vibration of rail and track plate should be focused on.Based on the calculation results,the vertical stiffness of the fasteners should be within the range of 20 MN/m-50 MN/m,the vertical stiffness of elastic support under the track plate should be within the range of 1.0×103MN/m-1.5×103MN/m,and the vertical stiffness of support of the U-girder should be within the range of 3×103MN/m-4×103MN/m.

vibration and wave;coupled vibration;U-shaped girder;track structure;multi-body dynamics

TU311.3；U441+.3

：A

：10.3969/j.issn.1006-1355.2017.04.026

1006-1355(2017)04-0132-06

2017-02-06

国家自然科学基金资助项目（51478184；51268015）

汪振国(1993－)，男，江西省九江市人，硕士研究生，主要研究方向为高架桥梁振动控制。E-mail:1449553252@qq.com.

雷晓燕(1956－)，男，教授，博士生导师。