大型风力机塔架固有频率分析
2017-09-03曾梦伟魏克湘李颖峰
曾梦伟,魏克湘,李颖峰,颜 熹
(1.湖南工程学院机械工程学院,湖南 湘潭 411104; 2.湘电风能有限公司,湖南 湘潭 411101)
大型风力机塔架固有频率分析
曾梦伟1,魏克湘1,李颖峰2,颜 熹1
(1.湖南工程学院机械工程学院,湖南 湘潭 411104; 2.湘电风能有限公司,湖南 湘潭 411101)
以2 MW水平轴风力发电机组为研究对象,基于有限元分析对风机整体结构进行数值仿真。主要研究地基土刚度、塔顶质量、混凝土基础、塔筒门洞、塔筒休息平台对风机整体结构固有频率的影响规律。仿真结果显示:风机整体结构固有频率随塔顶质量的增大而呈现减小趋势,风机叶片、轮毂和机舱设计可适当选择轻质量的材料;整体结构固有频率随地基土刚度的增加而快速增加,但增加到一定数值时这种趋势逐渐减小;塔筒底部简化为刚性约束将导致分析结果误差较大。
振动与波;风力发电机组;固有频率;有限元分析;结构动力学
风力发电作为21世纪的清洁能源之一,具有绿色无污染、可持续利用、技术最为成熟、最具规模开发条件和商业化发展前景等优点,受到了广泛的关注[1]。风机整体结构在风荷载与旋转动载荷的共同作用下会产生很大的振动,严重降低风机的结构强度,缩短整机的使用寿命。此外,这种振动将传递到地基,使得地基结构弱化,可能会导致风机产生一定程度倾斜,甚至倒塌。当风轮旋转频率与风机整体结构的固有频率接近时,会产生共振,影响风力发电机组性能,导致停机次数增多而降低年发电量[2–5]。因此,为了风力发电机组能安全有效运行,对风机结构进行动力特性分析显得十分重要,同时,对风机的结构优化设计也具有重要意义。
塔架是风机的主要承载部件,其性能直接影响整机的使用寿命,并间接影响风机生产厂家的名声。因此,国内外许多研究人员对塔架进行了相关研究。曹青等建立风力机塔架、基础与地基的相互作用三维有限元模型,分析了P-Δ效应、地基及地基与塔架基础的接触形式对塔架自振特性和地震时程响应的影响[6]。杨银锴等建立塔架动力学方程,并提出有效的减振控制方法[7]。柯世堂等通过在基础与土壤间增加弹簧和阻尼器来模拟其相互作用关系,并进行了风机结构响应分析[8]。陈志敏等基于Ansys对风机塔架结构进行了静力分析、模态以及屈曲分析,确定其稳定性和安全性[9]。周健等对风机基础-地基系统进行数值模拟,分析振动所导致的基础及土体的振动分布规律[10]。
基于有限元分析方法对风机整体结构进行数值仿真,探索风机整体结构动力性能的影响因素。主要研究地基土刚度、塔顶质量、混凝土基础、塔筒门洞、塔筒休息平台对风机整体结构固有频率的影响。
1 有限元模型的建立
以2 MW水平轴风力发电机组为研究对象,基于有限元分析方法对风机整体结构进行数值仿真,主要结构参数如下:塔筒高为76.9 m,塔顶直径为2.68 m,塔底直径为4.4 m,塔筒材料采用Q345-D钢材,最大壁厚为0.028 m,最小壁厚为0.012 m。混凝土基础弹性模量E=3.6×1010Pa,泊松比为0.2,密度为2 400 kg/m3,高度为2 m,直径为11 m。塔筒顶端机舱、轮毂、叶片总质量为99 t,塔顶总质量中心距塔架中轴线1.2 m,距塔顶高度1.1 m。
风力发电机塔筒内有许多的附属设备,由于结构简单且占风机总体比重较小,通常都忽略对其计算。将爬梯、通风口、电缆线等相关附属设备进行了适当简化,在保证计算精度的情况下提高分析速度,考虑塔筒门洞和休息平台对结构的影响。风机塔筒由多段组合而成,对连接的法兰和螺栓进行简化分析,每段塔筒之间采用刚性连接,地基土与混凝土基础间的作用关系通过一组弹簧进行等效,更好地模拟土壤刚度对整体结构动力特性的影响。建立有限元模型如图1、图2和图3所示。
2 模态分析
模态分析是研究结构动力特性的一种方法,在实际工程领域中得到了广泛的应用。模态是机械结构的固有振动特性,每一阶模态具有特定的固有频率、阻尼比和模态振型,因此,模态参数能为结构系统的振动特性分析及结构动力特性的优化设计提供依据[11]。通过分析风机整体结构的固有频率,并将其与风轮旋转激励频率进行比较,能有效避免风机整体结构发生共振。
在实际工程中,通常采用塔架简化模型,并将塔架底部视为固结来分析风机整体结构动力特性,忽略地基土刚度的影响,造成分析结果误差较大。因此,文中建立七种有限元模型对风机整体结构进行固有频率和振型分析,研究固有频率的影响因素。模型一:多段塔筒通过刚性连接,塔筒无门洞,塔筒底部为刚性约束。模型二:塔筒顶部设置立质量点,塔筒顶部与质量点通过无质量刚性梁连接,塔筒无门洞,塔筒底部为刚性约束。模型三:塔筒顶部设置质量块,塔筒顶部与质量块为刚性连接,塔筒无门洞,塔筒底部为刚性约束。模型四:塔筒顶部设置质量块,塔筒顶部与质量块为刚性连接,塔筒有门洞,塔筒底部为刚性约束。模型五:塔筒顶部设置质量块,塔筒顶部与质量块为刚性连接,塔筒无门洞,塔筒内部建立休息平台,休息平台与塔筒为刚性连接,塔筒底部为刚性约束。模型六:构建塔架混泥土基础,塔筒顶部与质量块为刚性连接,塔筒底部与基础为刚性连接,塔筒无门洞,基础底部为刚性约束。模型七:考虑基础与地基土之间弹性,通过一组弹簧模拟两者之间关系,塔筒顶部与质量为块刚性连接,塔筒底部与基础为刚性连接,塔筒无门洞。基于这七种模型进行模态分析,前8阶固有频率如表1所示。
大量的研究结果表明,风机整体结构低阶固有频率与风轮旋转激励频率较为接近,故对其低阶固有频率进行重点分析[12–14]。
比较模型一和模型二可知,考虑风机塔顶质量时,风机整体结构的固有频率有较大的下降,因此,风机叶轮和机舱的轻量化设计能有效避开共振。
比较模型二和模型三可知,风机整体结构前六阶固有频率非常相近,差别为0.14%左右,因此,塔顶质量块模型符合简化分析要求。
比较模型三和模型四可知,考虑塔筒门洞时,风机整体结构固有频率有所降低,1阶固有频率差别为2.1%,所以,门洞不能忽略计算。
比较模型三和模型五可知,塔筒内休息平台对风机整体固有频率影响较小,1阶固有频率差别约为1%。
比较模型三和模型六可知,考虑底部混凝土基础时,风机整体结构固有频率略有降低,1阶固有频率差别约为1%。

图1 整体机构有限元模型

图2 塔筒有限元模型

图3 地基土有限元模型
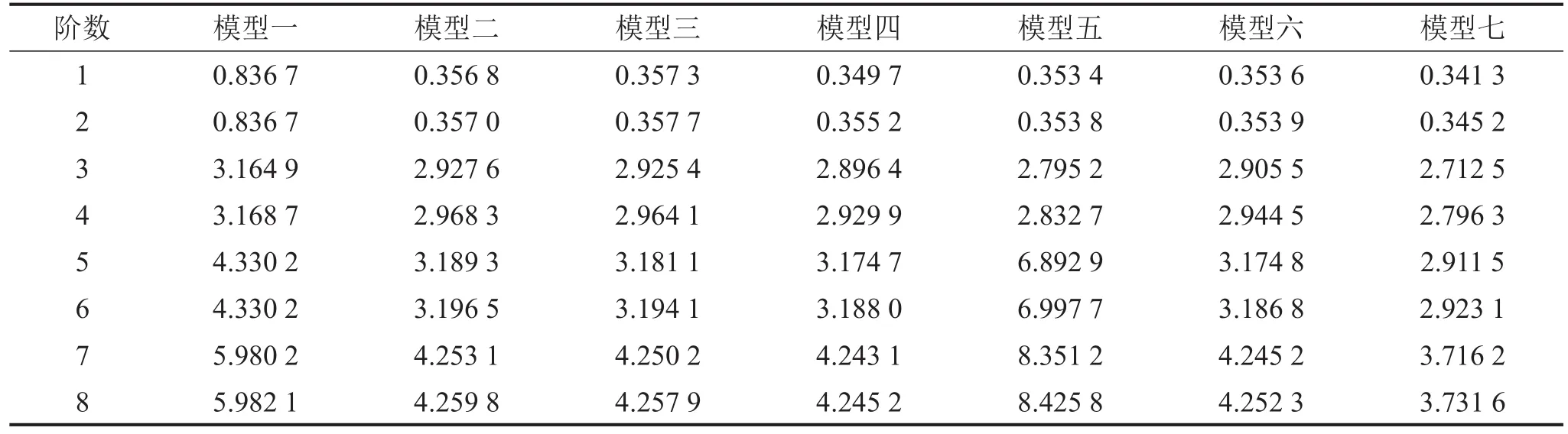
表1 前8阶固有频率/Hz
比较模型三和模型七可知,考虑地基土刚度时,风机整体结构的固有频率有较大的下降,1阶固有频率差别为4.5%,影响较大。
研究的风力发电机旋转速度为8 r/min~18 r/min,风轮旋转1P频率为0.13 Hz~0.3 Hz,3 P频率为0.39 Hz~0.9 Hz,计算得到的固有频率满足避开频率±10%的要求,风轮的激励频率不会导致风机整体结构共振,风机结构设计是安全可靠的。
3 风机整体结构模态影响因素
通过与简化模型的对比可知,风机整体结构模态的主要影响因素为塔架顶端质量和地基刚度的大小。因此,对塔顶质量、基础刚度与风机整体结构固有频率间的关系进行研究。
3.1 塔顶质量对固有频率的影响
研究的2 MW风机塔顶质量为99 t,选取模型三为研究对象,塔顶质量取值范围为75 t~105 t,基于有限元方法分析塔顶质量与1阶固有频率关系曲线如图4所示。

图4 塔顶质量与1阶固有频率关系图
由图4可知,风力发电机塔顶质量对整体结构固有频率影响较大,1阶固有频率随塔顶质量的增大而呈现减小趋势,风机叶片、轮毂和机舱设计可适当选择轻质量的材料,有利于避开共振。
3.2 地基刚度对固有频率影响
将塔筒底部进行刚性约束,忽略地基土的弹性作用,对风机整体结构进行动力特性分析,将导致分析结果出现较大误差。地基刚度在实际测量中很难得到准确的结果,存在一定误差。对地基土刚度与风机整体结构固有频率关系进行研究,为风机结构设计提供参考。对风机基础进行垂直方向位移约束,水平刚度变化范围1.0×109N/m~5.0×109N/m,前4阶固有频率变化如图5和图6所示。
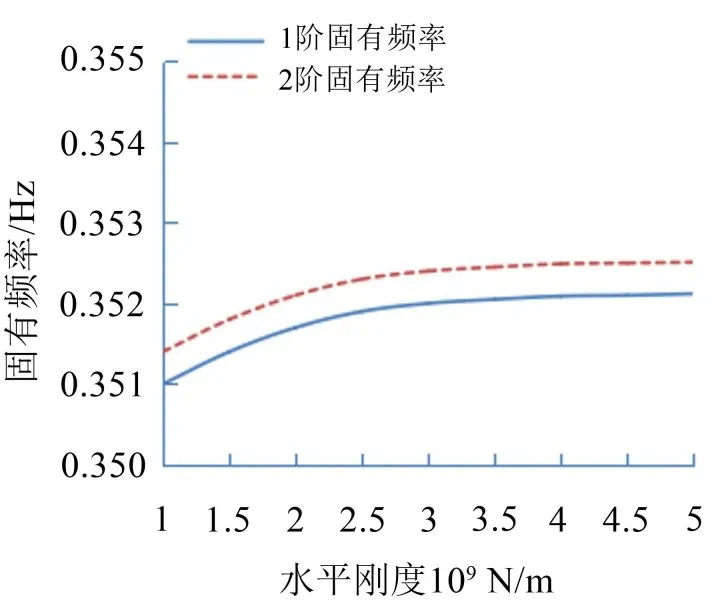
图5 水平刚度与1、2阶固有频率关系

图6 水平刚度与3、4阶固有频率关系
由图5和图6可知,风机整体结构随着水平刚度的增加而增加,水平刚度对1阶和2阶固有频率影响较小。地基刚度处于1.0×109N/m~3.0×109N/m时对高阶频率影响较大,随后曲线变化平缓并将到达一个固定值附近。
对风机基础进行水平位移约束,垂直刚度变化范围为1.0×1010N/m~6.0×1010N/m,前4阶固有频率变化如图7和图8所示。

图7 垂直刚度与1、2阶固有频率关系
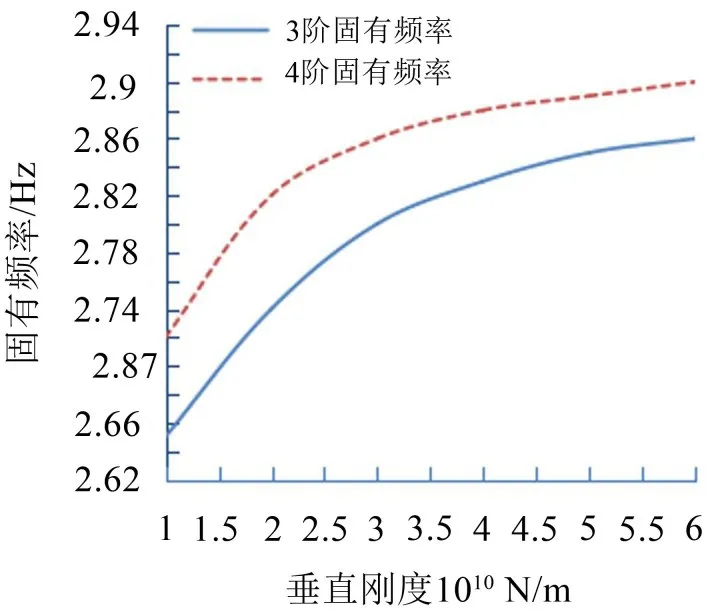
图8 垂直刚度与3、4阶固有频率关系
由图7和图8可知,风机整体结构频率随着垂直刚度的增加而增加。地基刚度为1.0×1010~3.5×1010N/m时对前4阶频率影响都较大,随后曲线变化相对平缓。因此,地基垂直刚度在风机结构设计时应重点考虑。
4 结语
(1)风力发电机塔筒顶端质量对整体结构固有频率影响较大,固有频率随塔顶质量的增大而呈现减小趋势。因此,风机叶片、轮毂和机舱在满足设计要求的条件下可适当选择轻质量的材料,避免整体结构频率和风轮旋转频率接近而产生共振,确保风力发电机组安全有效运行。
(2)研究的风力发电机旋转速度为8 r/min~18 r/min,风轮旋转1P频率为0.13 Hz~0.3 Hz,3P频率为0.39 Hz~0.9 Hz,计算得到的固有频率满足避开频率±10%的要求,风轮的激励频率不会导致风机整体结构共振,结构设计是安全的。
(3)考虑风机有门洞、休息平台和混凝土基础时,风机整体结构固有频率都略有降低,分析时应根据实际需求给予考虑。
(4)地基土刚度对整体结构的动力特性有较大影响,固有频率随刚度的增加而快速增加,增加到一定数值时趋势减小,若设塔筒底部为刚性约束进行分析,将导致分析结果误差较大。
[1]黄加明.风力发电的发展现状及前景探讨[J].应用能源技术,2015,34(4):291-291.
[2]何文博,廖明夫,王四季.某型风力机系统共振原因分析[J].噪声与振动控制,2013,33(5):97-101.
[3]聂国林,米良,程珩,等.基于APDL有限元法和正交试验的风力机塔架模态影响因素分析[J].太原理工大学学报,2016,47(2):254-258.
[4]曹必锋,衣传宝.风力机塔架在风-地震作用下的动力响应[J].噪声与振动控制,2014,34(4):205-208.
[5]王佼姣,施刚,石永久,等.考虑不同边界约束条件下的风电机塔架固有频率分析[J].特种结构,2011,5:14-17+117.
[6]曹青,张燎军,汪清.地基基础对风力发电机塔架系统地震响应的影响研究[J].水力发电学报,2011,30(6):122-126.
[7]杨银锴,卢晓光,岳红轩,等.基于有限元结构动力学模型的塔架振动分析[J].机械与电子,2015,35(3):34-38.
[8]柯世堂,王同光,曹九发,等.考虑土-结相互作用大型风力发电结构风致响应分析[J].土木工程学报,2015,64(2):18-25.
[9]陈志敏,孙华东.水平轴风力发电机塔架的有限元分析[J].制造业自动化,2015,39(4):47-48.
[10]周健,金炜枫,金卫华,等.风力发电机地基的现场加速度测试和数值模拟[J].地震工程学报,2011,33(s1):257-260.
[11]梁君,赵登峰.模态分析方法综述[J].现代制造工程,2006,39(8):139-141.
[12]张丰豪,何榕.基于柔性多体动力学的风力发电机固有振动频率研究[J].中国电机工程学报,2014,34(11):1807-1814.
[13]ADHIKARI S,BHATTACHARYA S.Dynamic analysis of wind turbine towers on flexible foundations[J].Shock&Vibration,2012,19(1):37-56.
[14]SATARI PEMA,HUSSAIN SES.Vibration based wind turbine tower foundation design utilizing soil-foundationstructure interaction[C].Seismic Engineering Conference,2008,1020(1):577-584.
Natural FrequencyAnalysis of a Wind Turbine Tower
ZENG Meng-wei1,WEI Ke-xiang1,LI Ying-feng2,YAN Xi1
(1.Department of Mechanical Engineering,Hunan Institute of Engineering,Xiangtan 411104,Hunan China;2.XEMC Windpower Co.Ltd.,Xiangtan 411104,Hunan China)
The dynamic characteristics of a 2 MW horizontal axis wind turbine are studied numerically by means of finite element analysis.The influence of soil foundation rigidity,tower top mass,concrete foundation,tower door and resting platform on the natural frequencies of the whole structure of the wind turbine is analyzed.The simulation results show that the natural frequencies of the whole structure of the wind turbine decrease as the tower top mass increases,and increase rapidly and then slowly as the rigidity of the soil foundation increases.When the bottom of the tower is simplified as a rigid constraint,results of the simulation analysis will have large errors.
vibration and wave;wind turbine;natural frequency;FEM;structural dynamics
TH113.1
:A
:10.3969/j.issn.1006-1355.2017.04.007
1006-1355(2017)04-0030-04
2017-01-06
国家自然科学基金资助项目(11472103)
曾梦伟(1993-),男,湖南省娄底市人,硕士生,主要研究方向为动力机械设计与制造技术。
魏克湘,男,硕士生导师。
E-mail:kxwei@hnie.edu.cn
