基于机会辐射源的弹载探测卫星优选方法

肖泽龙， 王华， 周鹏， 韩璐霞， 王元恺， 李潇， 逯暄

(1.南京理工大学 电子工程与光电技术学院， 江苏 南京 210094; 2.中国运载火箭技术研究院 研究发展中心， 北京 100076；3.山西大学 电子信息工程系， 山西 太原 030006)

基于机会辐射源的弹载探测卫星优选方法

肖泽龙1， 王华2， 周鹏1， 韩璐霞1， 王元恺1， 李潇2， 逯暄3

(1.南京理工大学 电子工程与光电技术学院， 江苏 南京 210094; 2.中国运载火箭技术研究院 研究发展中心， 北京 100076；3.山西大学 电子信息工程系， 山西 太原 030006)

弹载无源探测器由于自身高速运动，探测系统几何配置关系变化迅捷，卫星的选取直接影响系统探测能力，因此提出相应的卫星优选方法极为重要。针对该问题，以北斗卫星导航系统(BDS)卫星作为机会辐射源，给出了弹载无源探测器的分辨力要求；利用双站模糊函数和角分辨力公式推导出目标分辨力与探测系统几何配置间的定量关系；结合分辨力要求反推出对空间几何配置关系的约束条件，给出了相应的BDS卫星优选方法。仿真结果验证了该卫星优选方法的可行性和有效性。

雷达工程； 北斗卫星导航系统； 弹载； 无源探测器； 分辨力； 优选方法

0 引言

基于机会辐射源的无源探测技术是利用第三方发射的非合作电磁信号对目标进行探测和定位。目前，基于机会辐射源的无源探测研究主要集中于地基的固定平台[1]，少量针对仅能小范围慢速机动的车载平台[2]和机载平台[3]，其无源探测系统在设计时即可选定辐射源的种类和发射站的位置。

现有研究中各类常见民用信号均曾被选用作为机会辐射源。文献[4]利用GPS全球定位系统、DVB-S数字卫星广播电视和DVB-T地面数字广播电视 3种不同机会辐射源混合对近海多目标进行了探测，并发现利用多种机会辐射源比利用单种机会辐射源时无源雷达能降低目标发现门限和虚警概率；文献[5]提出了一种全球移动通信系统(GSM)辐射源雷达干扰抑制技术，不仅消除了主基站的干扰，还对其他同频基站的干扰进行了抑制；文献[6]给出了一种切实可行的外辐射源雷达网络优化系统定位性能评估方案；文献[7]给出了在机会辐射源雷达系统中选择机会辐射源时考虑的三原则：辐射源可用性及辐射源功率、辐射源信号的波形特征和不同的应用领域。

当基于机会辐射源的无源探测技术应用于横跨多区域且高速运动的弹载平台时，机会辐射源的选取将变得更为复杂。由于弹载平台在高空高速运动，短时间内横跨多个区域工作，造成探测系统的几何配置关系随时间快速变化，所以弹载无源探测系统在选取机会辐射源时，除了考虑文献[7]的三原则外，还需要根据其所在的空间位置和系统几何配置关系，不断从其所接收的来自不同方向的同种辐射源中优选出最佳辐射源。若仅根据卫星与弹载探测器间的距离长短来选取卫星，所选卫星信号未必满足探测系统要求。针对该问题，本文在选用北斗导航卫星系统(BDS)作为机会辐射源，弹道导弹作为载体，航母作为目标的前提下，从探测目标所需分辨率的角度考虑，给出了一种对机会辐射源卫星优选的方法。

1 基于BDS的弹载无源探测系统几何配置

基于BDS的弹载无源探测系统的空间几何配置关系如图1所示。无源探测器由直达信号接收通道和目标信号接收通道组成。在探测过程中，一部分BDS卫星信号直接到达弹载无源探测器，成为直达波，被探测器直达信号通道接收作为参考信号；另一部分BDS信号照射在目标上，成为照射波，然后被目标反射后再到达无源探测器，成为反射波，并被无源探测器目标信号通道接收作为目标信号；探测器在任意时刻、任意位置至少能接收到4颗或以上BDS卫星发射的直达波信号[8]。

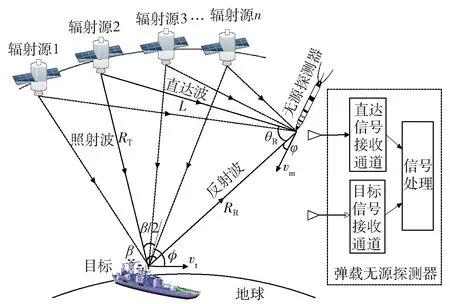
图1 基于BDS的弹载无源探测器系统空间几何配置图Fig.1 Space geometric configuration of missile-borne passive detector based on BDS

图1中：辐射源为BDS卫星，RT是BDS卫星到目标的距离，RR是目标到无源探测器的距离，且R=RR+RT可由探测器目标信号接收通道测得；L是BDS卫星到无源探测器的距离，可由探测器直达波接收通道测得；θR是直达波与目标反射波之间的夹角，可由阵列天线测得；vm是导弹速度，φ是导弹速度与无源探测器和目标之间连线的夹角，vt是目标速度，β是双基角，φ是目标速度与双基角二分线的夹角。

2 基于BDS的弹载无源探测器的最大可探测距离及目标分辨力分析

2.1 最大可探测距离

BDS卫星距地面20 000～35 000 km，到达地表的信号强度仅为-144.5 dBW，经目标反射后的回波信号更弱。基于卫星辐射源的双基地雷达的最大探测距离公式[9]为

Rmax={(ρ0AσΔfπτk)/(ρrλ2G)}1/2,

(1)

式中：ρ0是接收机输入端平均信噪比；A为接收天线有效面积；σ为目标雷达散射截面积(RCS)；Δf为接收机带宽；τk为接收机相关积分时间；λ为BDS卫星信号载波波长；G为天线增益；ρr为在给定的检测概率PD和虚警概率PF约束下要求的信噪比，其计算公式为

ρr=ρ1(PD,PF)+Li(ρ1,NH)+Lf(PD,PF)/NH-10lgNH,

(2)

式中：ρ1为待检测信号的单脉冲信噪比；NH为最大非相干采样数；Li为非相干积累损耗；Lf为慢目标起伏损耗。此外，根据相关接收机理论，接收机的灵敏度为

ρs=kT0Na/τk,

(3)

式中：k是玻尔兹曼常数；T0是绝对温度；N是接收机噪声系数；a是信号识别系数。

本文选用灵敏度为-165 dBW的接收机，取信号识别系数为32，则由(3)式可知τk为0.010 1 s. 为了保证能检测出目标接收机输入端信噪比，ρ0取20 dB. BDS接收机天线增益为25 dB，天线有效面积为0.36 m2，最大非相干采样点数取112，接收机带宽取BDS信号带宽为8 MHz，BDS卫星信号载波波长0.12 m. 在检测概率PD=0.90、虚警概率PF=1.155×10-6的条件下，航母目标RCS取5 000 m2[10]，则由(1)式、(2)式可计算出：ρr=-1.5 dB，最大可探测距离Rmax=120 km，且总积累时间T=1.13 s，满足一般战术要求。

2.2 目标分辨力分析

目标分辨力是指两个具有大致相等回波幅度和任意恒定相位的目标在角度、距离、速度上能被区分的程度，是雷达系统的一种固有能力。

2.2.1 距离分辨力与速度分辨力

模糊函数是研究目标距离分辨力和速度分辨力时有效的数学工具。本文选用BDS信号的粗码作为辐射源分析本系统双站模糊函数。

由基于BDS的弹载无源雷达系统空间几何配置关系中已知的条件参数计算出本系统的双站模糊函数[11]为

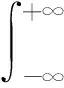
(4)

式中：RRH、vtH为模糊函数中的距离和速度变量；RRa、vta、L、φ、φ是初始条件下的参数，属于常数；τa、τH为目标信号时延；fa、fH为目标信号多普勒频移；下标a、H分别表示目标初始参数值和t时刻参数值。X=a,H,τX、fX的表达式为

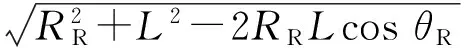
(5)

式中：fL是BDS信号载频；c为光速。

假设系统初始参数为RRa=120 km,vta=90 m/s，φ=0°,φ=45°,联合(4)式、(5)式在不同θR的条件下仿真BDS信号的模糊函数，并得到双站模糊函数图如图2所示。

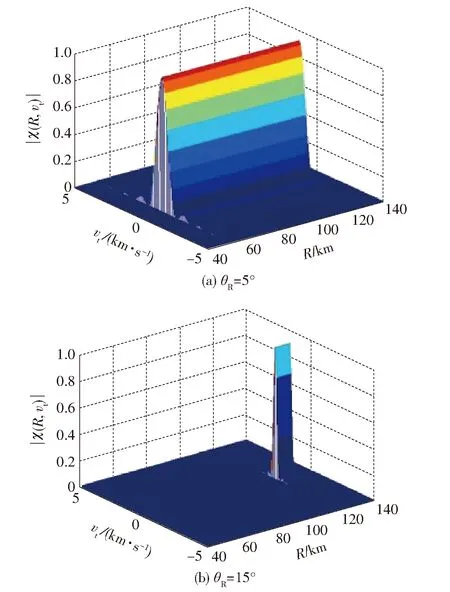
图2 BDS信号在不同θR下的双站模糊函数图Fig.2 Graph of bistatic ambiguity function of BDS signal at different θR

由图2中可知：基于BDS的弹载无源探测器的距离分辨力和速度分辨力与θR是呈正相关的：随着θR增大，无源探测器的速度分辨力和距离分辨力均越来越好。

2.2.2 角度分辨力

由于收发分置，双基地雷达不便于直接使用角度参数来表示目标的分辨角。在双基地雷达中，角度分辨力是用方位向分辨率进行表示，其定义式为

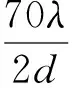
(6)

式中：Δθr为接收天线单程方向图半功率波束宽度；d是天线物理直径。代入系统参数则有

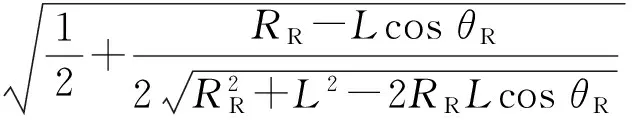
(7)

由(7)式可知：无源探测器的方位向分辨率是与θR呈正相关：当RR一定时，随着θR增大，无源探测器的方位向分辨率越来越好。

3 探测器轨迹分段及各阶段探测目标所需分辨力要求

弹道导弹命中目标的过程分为自控飞行段和自导飞行段。自导飞行段开始后，探测器开始捕捉目标。从图3可知，弹载无源探测器从开机至击中目标可分为3个阶段：搜索阶段、跟踪阶段、识别阶段。

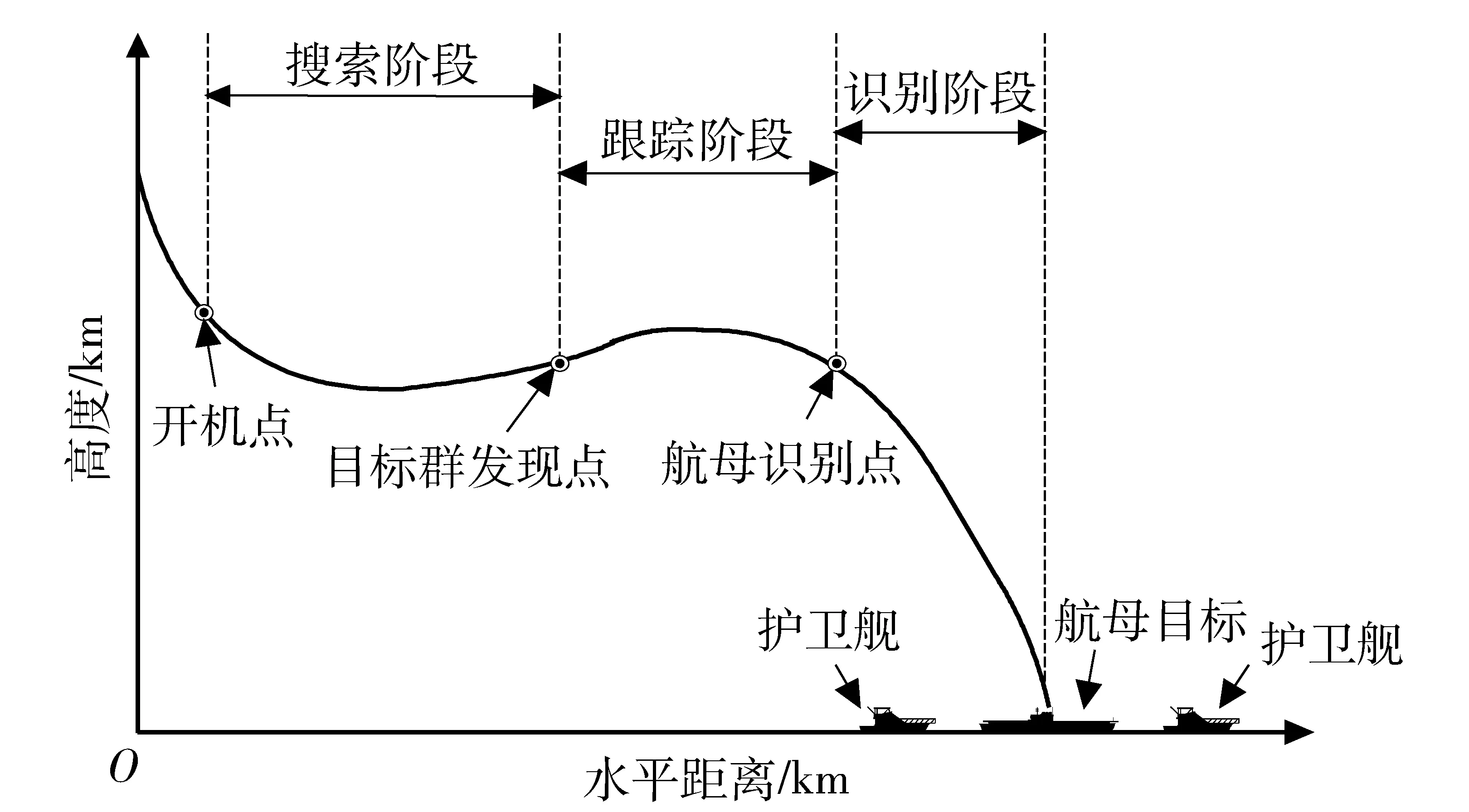
图3 导弹自导飞行段分段图Fig.3 Missile homing flight segment

本文以某航母设为目标为例，在作战模式下的典型航母编队队形[12]中，护卫舰分布在以航母为圆心的两个圆上，内层圆半径一般为8～10 n mile，外层圆的半径通常为50 n mile，此外，还有一艘快速战斗支援舰在离航母约为5 n mile左右待命支援。一般情况下，航母战斗群中的所有战舰以相同速度同向行驶，并且行驶速度远小于导弹速度，因此本文不考虑速度分辨力的影响。

无源探测器在不同阶段对目标分辨力要求不同。搜索阶段：无源探测器以±φ(0<φ<90°)的范围在方位向进行横扫，辅以导弹前进的速度形成一个扇环形的搜索区域。本阶段仅需探测航母战斗群的位置，对系统目标分辨力要求不高。综合权衡目标分辨力和对目标的定位精度，在本阶段无源探测器的距离分辨力和方位向分辨率应优于16 n mile(29.6 km)。

跟踪阶段：无源探测器锁定航母战斗群并保持跟踪状态，因此对无源探测器的分辨力要求与搜索阶段的要求相同，即距离分辨力与方位向分辨率均应优于16 n mile(29.6 km)。

识别阶段：为保证能在航母战斗群中区分出航母，无源探测器需将航母与其距离最近的战斗支援舰区分开，因此无源探测器的距离分辨力和方位向分辨率均应优于9.26 km.

4 BDS卫星优选原则

4.1 探测器系统的空间几何配置约束条件

由2.2节分析可知，在不同阶段，需要根据目标分辨力与探测系统几何配置间的定量关系来对无源探测系统的几何配置关系进行约束。

定量研究目标距离分辨力和速度分辨力时通常采用-3 dB(半功率点)模糊度图，该模糊度图即显示出距离分辨力和速度分辨力的大小。由计算仿真得出的图4可知，距离分辨力和速度分辨力均随着θR的增大而越来越好，并且从θR≥20°开始，距离分辨力就达4.9 km，远满足无源探测器在各阶段的分辨力要求，因此主要依据方位向分辨率对不同阶段的探测系统几何配置关系进行约束。

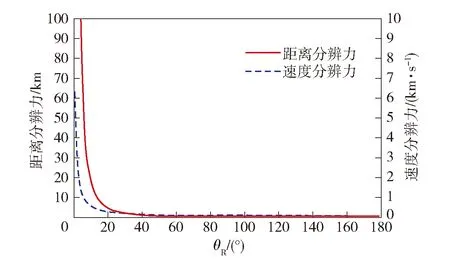
图4 距离分辨力和速度分辨力与θR的关系Fig.4 Relationship among range resolution， velocity resolution and θR

搜索阶段与跟踪阶段：无源探测器方位向分辨力应优于16 n mile，探测器开机点离目标的距离按最大探测距离计算，代入(8)式，获得方位向分辨率与θR间的定量关系，如图5中实线所示。为保证在该两阶段无源探测器的方向位分辨率ΔR≤29.6 km，则应有θR≥104°. 同理在识别阶段：方位向分辨率应优于5 n mile，弹道导弹一般在距离目标约45 km处便开始进入识别阶段[13]，即取RR=45 km代入(8)式，其结果如图5中虚线所示。为了保证无源探测器在该阶段的方位向分辨率ΔR≤9.26 km，则应有θR≥143°.

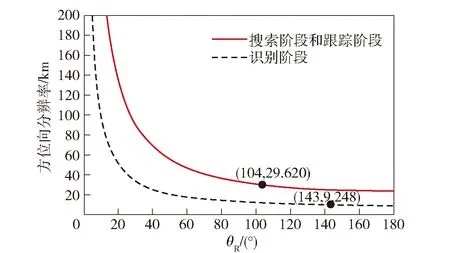
图5 不同阶段时方位向分辨率与θR的关系Fig.5 Relation of azimuth resolution and θR at different stages

4.2BDS卫星优选

BDS卫星采用2000中国大地坐标系(CGCS2000)，坐标系中任意一点可用坐标(Bg,Lg,Hg)或者(X,Y,Z)表示，Bg、Lg、Hg分别表示大地纬度、大地经度和大地高程。两种坐标相互间的关系转换式[8]为

(8)

式中：M=a/W,W=(1-e2sin2Bg)1/2,e2=(a2-b2)/a2，a、b分别是CGCS2000定义中CGCS2000椭球的长半径和短半径。

基于BDS的弹载无源探测器在进行BDS卫星优选时，不同阶段可利用的已知条件不同，对探测系统的几何配置关系约束也不同。

搜索阶段：导弹沿着水平方向直线飞行，同时无源探测器以速度矢量vm为中轴线进行±φ的扇环搜索。无源探测器在本阶段时探测系统几何配置关系如图6所示。

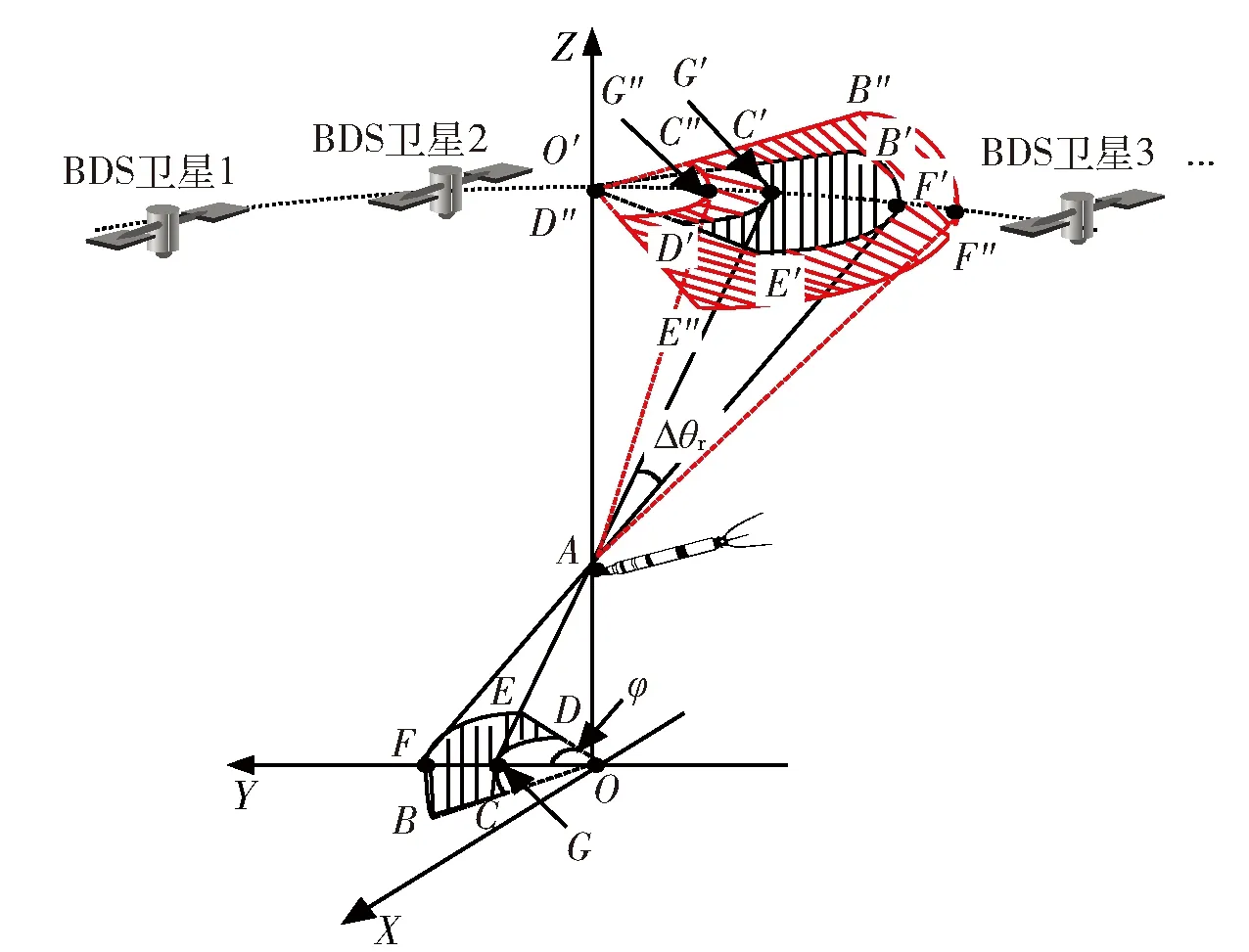
图6 搜索阶段探测器系统几何配置关系Fig.6 Geometric configuration of detector system in search phase

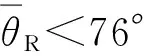
无源探测器位置A点(Bg0,Lg0,Hg0)可由BDS信号测得。另设O′点(Bg1,Lg1,Hg1)、F″点(Bg2,Lg2,Hg2)、G″点(Bg3,Lg3,Hg3)，经过(8)式转换后的坐标分别为A(X0,Y0,Z0)、O′(X1,Y1,Z1)、F″(X2,Y2,Z2)、G″(X3,Y3,Z3)，且有Hg1=Hg2=Hg3，Bg1=Bg0，Lg1=Lg0.AF=Rmax且Rmax、vm和Δθr均可由探测系统给出，vmOXY是vm在OXY平面的分量，则由几何关系可知扇面区域O′B″E″的方程为

(9)

因此，无源探测器工作在搜索阶段时，所选取的BDS卫星所在位置(Bg,Lg,Hg)应满足(9)式。

跟踪阶段：无源探测器在本阶段时探测系统几何配置关系如图7所示。

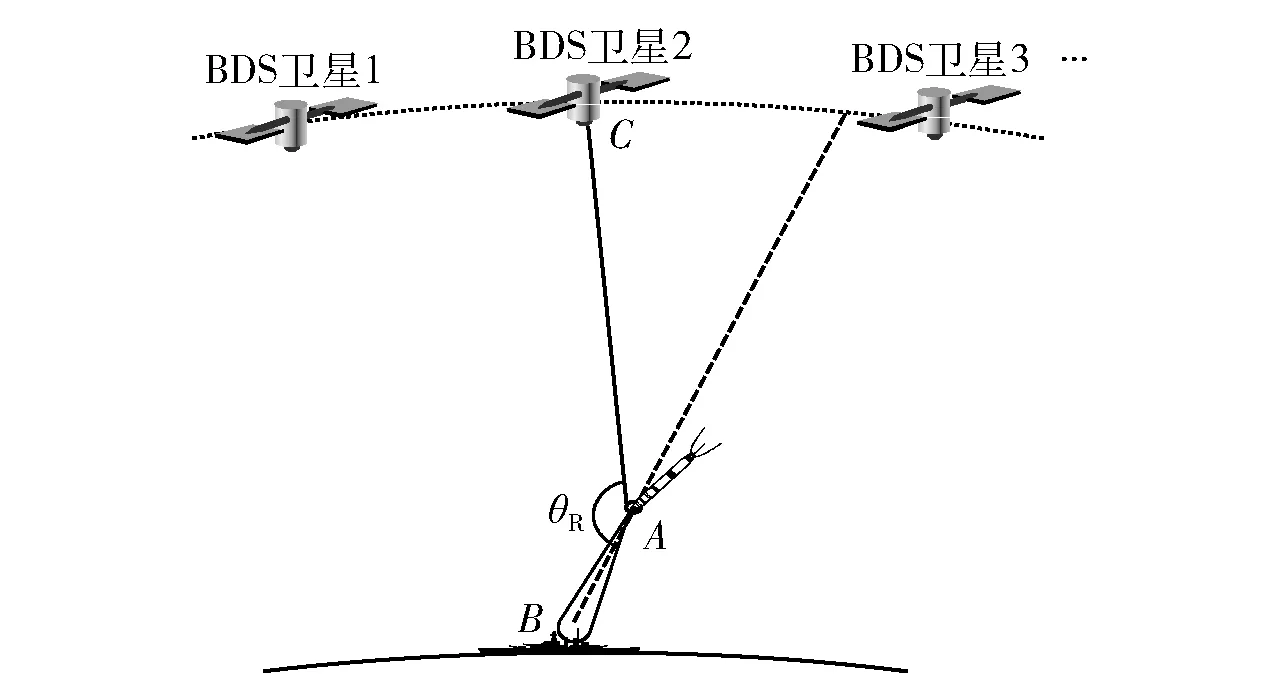
图7 跟踪阶段探测器系统几何配置关系Fig.7 Geometric configuration of detector system in tracking phase

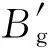
(10)

为了满足探测器系统的空间几何配置约束条件，必须满足θR≥104°，则有

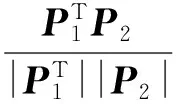
(11)

式中：|P2|为点A与点C的距离，即为图1中BDS卫星到无源探测器的距离L.

因此，无源探测器工作在跟踪阶段时，所选取的BDS卫星所在位置(X,Y,Z)应满足(11)式。

识别阶段：在本阶段已知的探测系统条件与跟踪阶段相同，因此在本阶段的探测系统几何配置关系与跟踪阶段的相同。为满足探测器系统的空间几何配置约束条件，必须满足θR≥143°，则有

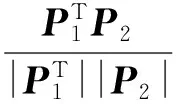
(12)

因此，无源探测器工作在识别阶段时，所选取的BDS卫星所在位置(X,Y,Z)应满足(12)式。

5 仿真验证

本文借助STK8卫星工具包软件和Matlab软件进行仿真实验：设定时间为2016年11月11日17时整，目标设于北纬10°、东经114°处；以目标为原点O，正东方向为X轴，正北方向为Y轴，依右手规则设立Z轴建立探测系统坐标系，坐标单位为km；设导弹从我国内陆发射并于在探测系统坐标系的(-20 km,120 km,40 km)处再次进入大气层，并最终击中目标；借助STK8软件仿真找出该时刻在目标附近区域所能观测到的BDS卫星如图8所示，使用Hermit法模拟出导弹从再次进入大气层到击中目标的过程轨迹如图9所示。依图8中所示，目标位于中国南沙群岛区域，图8中与白线连接的是在该时刻目标区域能观测到的所有BDS卫星，共20颗，在该时刻可见MEO星在CGCS2000和探测系统坐标系中的坐标如表1所示。选择点At1,At2,At3时刻分别代表搜索阶段、跟踪阶段和识别阶段，如图9所示。探测系统坐标系中三点坐标分别为：At1(-17 km，114 km，33 km)，即弹目距离120 km，且该时刻弹载探测器速度矢量vt1=(0.89 km/s,-2.16 km/s,-2.29 km/s);At2(-8 km,77 km,20 km)，即弹目距离80 km;At3(-2 km,23 km,33 km)，即弹目距离40 km.t1、t2、t3时刻相隔很短，故认为3个时刻BDS卫星的位置不变。

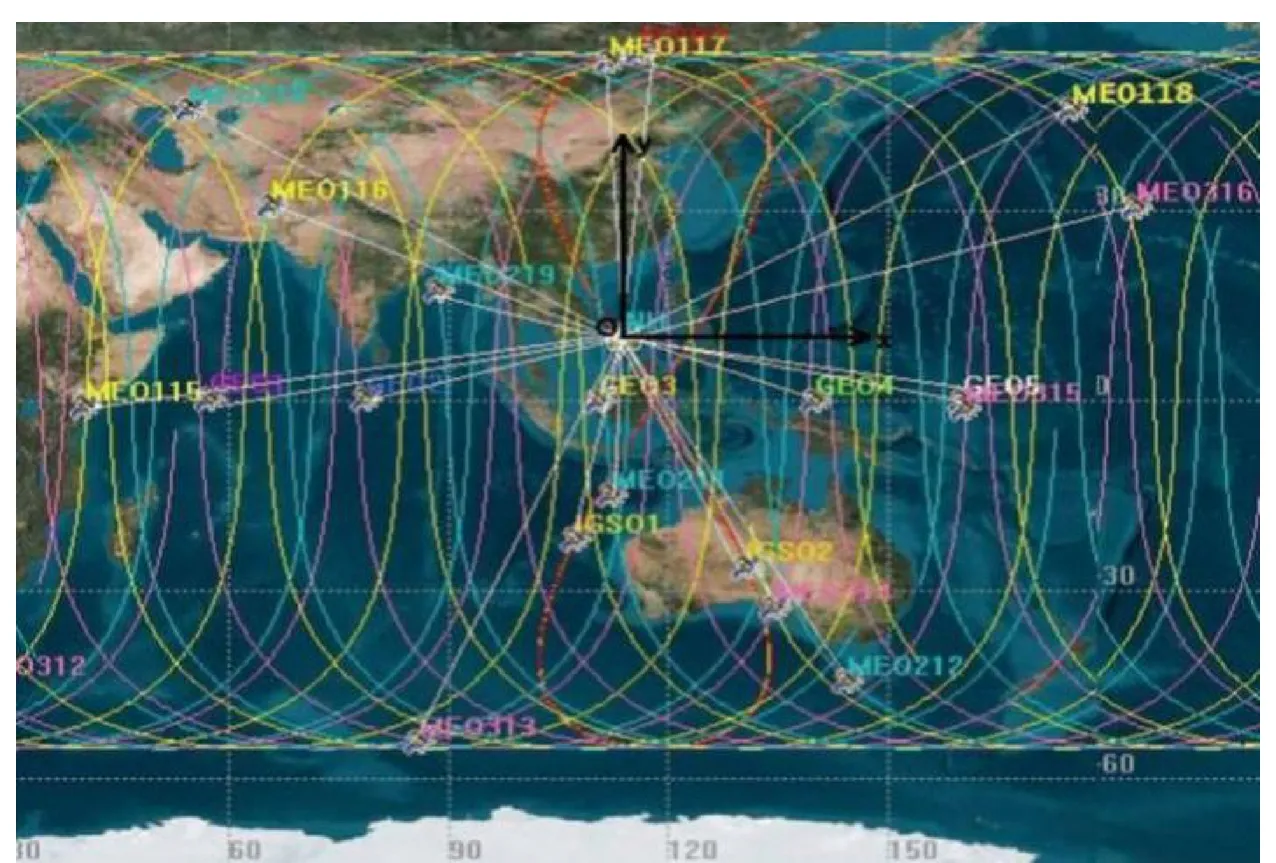
图8 可见星示意图Fig.8 Sketch map of visible star

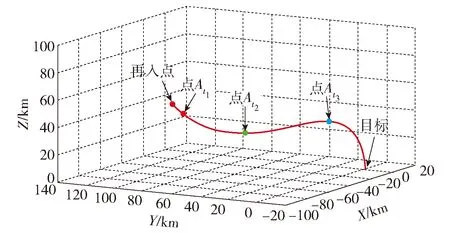
图9 弹载探测器轨迹模拟图Fig.9 Trajectory simulation of missile-borne detector

依表2所示，利用不同的BDS卫星作为机会辐 射源，弹载无源探测系统所表现出的性能不同。 由于一般需要3～4个机会辐射源才能实现对目标的有效定位，因此本文实验将分别使用就近法和本文提供的卫星优选方法从12颗BDS卫星中选择4颗卫星。

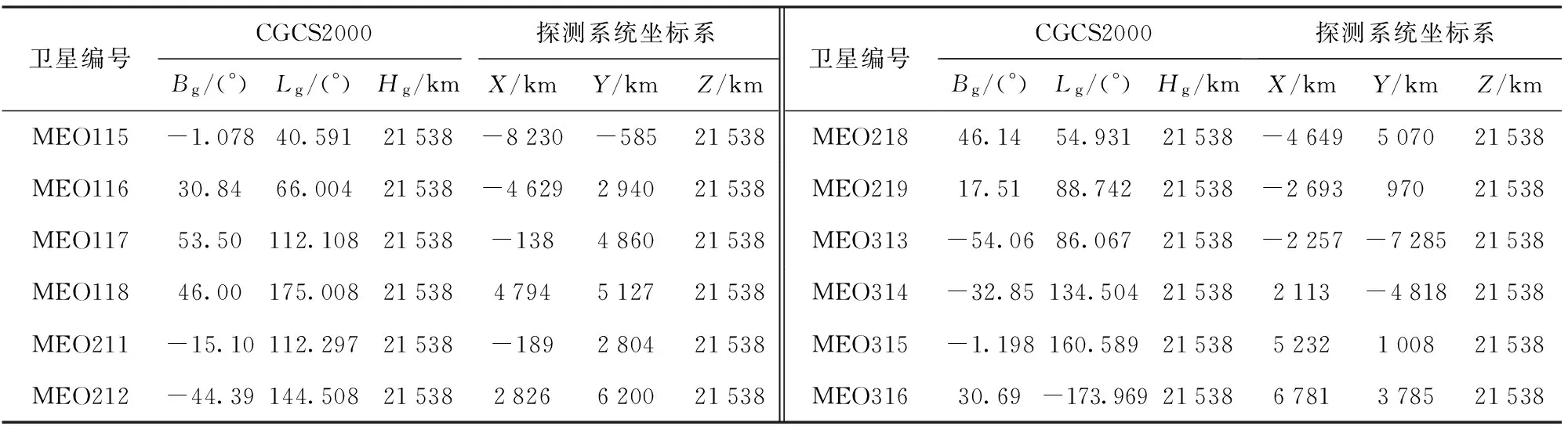
表1 2016年11月11日17时整目标区域BDS可见星坐标

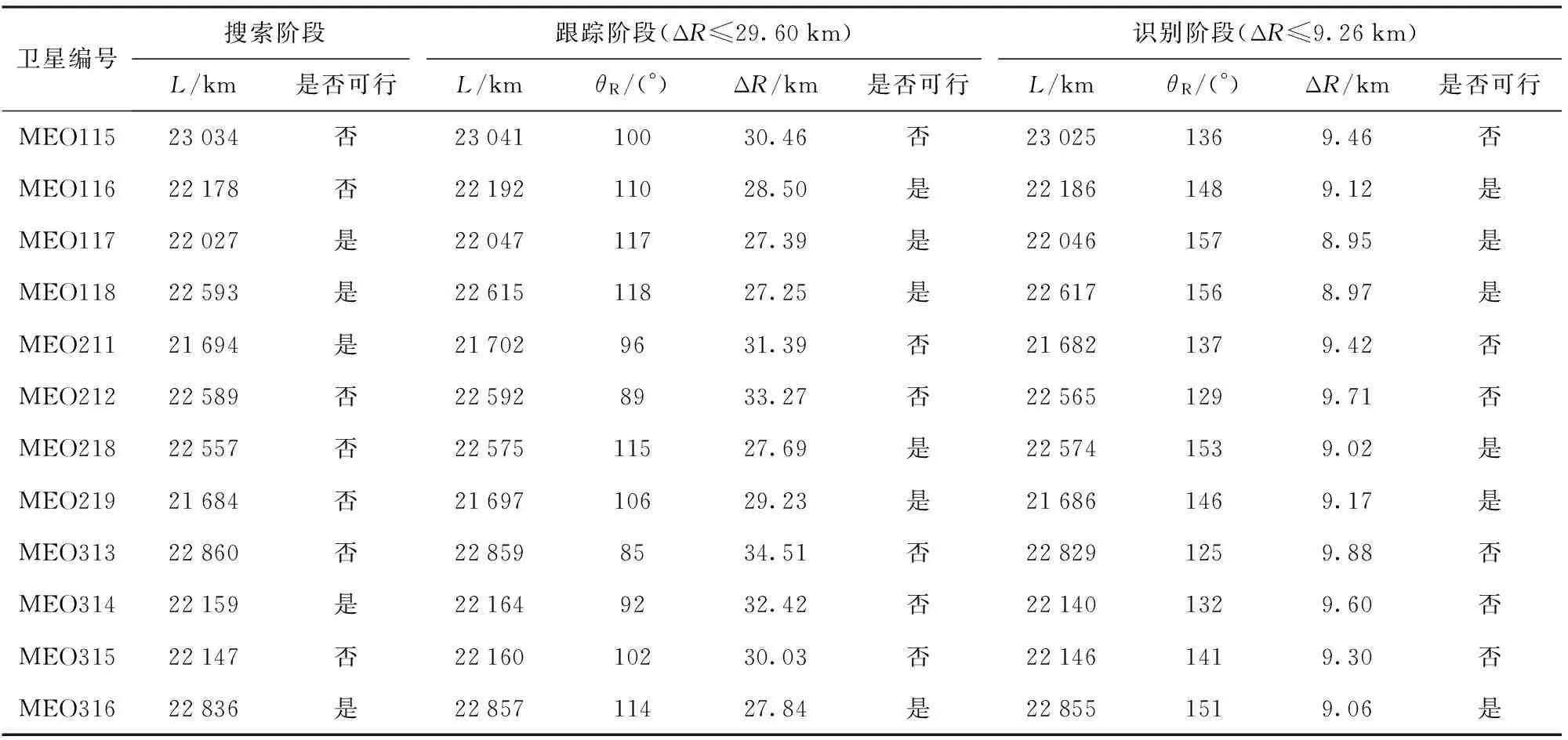
表2 各BDS卫星在弹载无源探测系统中的性能

就近法：通过判断BDS卫星与弹载探测器间的距离远近进行选择。依表3可知，在t1、t2、t3时刻距离弹载探测器最近的4颗卫星为MEO219、MEO211、MEO117、MEO315. 在搜索阶段，MEO211和MEO117满足(9)式，符合探测系统要求；MEO219和MEO315不满足(9)式，不符合探测系统要求。在跟踪阶段和识别阶段，MEO219和MEO117符合(11)式、(12)式，满足系统要求；MEO211和MEO315不满足(11)式、(12)式，不符合探测系统要求。

本文提供的卫星优选法：将12颗卫星参数按照距弹载探测器由近到远的顺序依次输入判决式进行选择。依表2可知，在搜索阶段所选卫星为MEO211、MEO117、MEO314、MEO316，在跟踪和搜索阶段所选卫星为MEO219、MEO117、MEO116、MEO218. 由此可知，通过卫星优选法所选出的卫星全部满足弹载探测系统在不同时刻对目标的方位向分辨率要求。

通过上述仿真实验进行对比可知，本文提出的卫星优选方法是可行且有效的，能满足弹载无源探测系统在不同时刻对目标的探测性能要求。

6 结论

与地基、机载和车载平台不同，弹载平台具有工作地点不固定、单次工作横跨区域范围广、自身运动速度快的特点，会引起可供探测系统选择的机会辐射源卫星具有随机性以及探测系统的几何配置关系快速发生变化，而选取不同位置的辐射源卫星和不同的探测系统几何配置关系会导致无源探测系统的目标分辨力不同，因此基于机会辐射源的弹载无源探测系统在工作时需要从所接收到的多个信号中不断地优选出最适合该时段的辐射源卫星。针对该问题，本文提出了适用于基于星载机会辐射源的弹载无源探测系统对辐射源卫星优选的方法，进行仿真实验验证了该方法的可行性与有效性，为弹载无源探测系统机会辐射源的自适应选取提供理论参考依据。本文仅以BDS信号作为一种机会辐射源为例讨论卫星优选原则，实际上为了提高探测器的抗干扰性能，应机会选取多种辐射源，但二者思路相通，本文方法不失一般性。对多种辐射源的自适应选取也作为后续工作的方向之一进行展开。

References)

[1] Kuschel H,O’Hagan D. Passive radar from history to future[C]∥2010 International Radar Symposium . Vilnius, Lithuania:IEEE,2010:1-4.

[2] Kulpa K,Malanowski M,Samczyński P, et al .Passive radar for airborne platform protection[J].International Journal of Microwave & Wireless Technologies, 2012,4(4):137-145.

[3] Brown J,Woodbridge K,Griffiths H,et al. Passive bistatic radar experiments from an airborne platform[J]. IEEE Aerospace & Electronic Systems Magazine, 2012,27:50-55.

[4] Biagi M, Rinauro S, Colonnese S, et al. Near-sea multi-target opportunistic multiple-input multiple-output detection[C]∥OCEANS. St. John′s, NL, Canada: IEEE, 2015:1-5.

[5] 张良俊，杨杰，卢开旺.GSM辐射源雷达干扰抑制技术[J].电子学报，2014，42(9)：1852-1856. ZHANG Liang-jun, YANG Jie,LU Kai-wang. Clutter suppression technique in GSM based passive bistatic radar[J]. Acta Electronica Sinica, 2014,42(9): 1852-1856.(in Chinese)

[6] 谢锐，万显荣，方高，等.外辐射源雷达网络定位性能评估与实验验证[J].电子与信息学报，2016，38(3)：753-757. XIE Rui, WAN Xian-rong, FANG Gao, et al.Evaluation and experimental validation of the performance evaluation of the radar network for the external radiation source [J]. Journal of Electronics and Information,2016,38 (3): 753-757.(in Chinese)

[7] 徐世友，陈曾平.机会照射源雷达系统中机会辐射源的选择[J].现代雷达，2007，29(10)：16-19. XU Shi-you, CHEN Zeng-ping. Selecting of illuminator on opportunistic illuminator radar system[J]. Modem Radar,2007,29(10):16-19.( in Chinese)

[8] 李文天.GPS原理及应用[M].北京：科学出版社， 2003：5-32. LI Wen-tian. Understanding GPS: principles & applications [M].Beijing: Science Press, 2003: 5-32. (in Chinese)

[9] Mojarrabi B,Homer J,Kubik K,et al. Power budget study for passive target detection and imaging using secondary applications of GPS signals in bistatic radar systems[J]. IEEE International Geoscience & Remote Sensing Symposium,2002,1(1):449-451.

[10] Williams P D L,Cramp H D,Curtis K. Experimental study of the radar cross-section of maritime targets[J]. IEEE Journal on Electronic Circuits & System,1978,2(4): 121-136.

[11] 郭强，李玮锋，马长征，等.一种新的双基地探测系统数学模型及模糊函数的建立方法[J].兵工学报，2009， 30(11)：1457-1462. GUO Qiang, LI Wei-feng, MA Chang-zheng,et al. A novel framework of the mathematical model and ambiguity function for a bistatic detection system[J].Acta Armamentarii,2009,30(11):1457-1462.(in Chinese)

[12] 赵晓春.美国航母编队队形与反潜能力分析[J].舰船科学技术，2013，35(9)：143-148. ZHAO Xiao-chun.Analysis of the anti-submarine mode and capability of the U.S.Navy carrier group[J].Ship Science and Technology,2013,35(9):143-148. (in Chinese)

[13] 刘亿，孙洲.反舰导弹末制导雷达最佳开机点的确定方法[J].战术导弹技术，2015(4)：82-85. LIU Yi,SUN Zhou.The method of determining the best start point of anti-ship missile terminal guidance radar[J].Tactical Missile Technology,2015(4):82-85.(in Chinese)

A Satellite Selection Method for Missile-borne Detection System Based on Opportunity Illuminators

XIAO Ze-long1， WANG Hua2， ZHOU Peng1， HAN Lu-xia1， WANG Yuan-kai1， LI Xiao2, LU Xuan3

(1.School of Electronic Optical Engineering, Nanjing University of Science and Technology,Nanjing 210094, Jiangsu, China;2.Research and Development Center, China Academy of Launch Vehicle Technology，Beijing 100076, China;3.Department of Electronic Information Engineering,Shanxi University,Taiyuan 030006, Shanxi, China)

The geometric configuration relationship of detection system changes rapidly due to the high speed movement of missile-borne passive detector. The detection ability of the system highly relies on the selection of satellites. To solve this problem, BDS (BeiDou navigation satellite system) satellites are selected as opportunity illuminators, and the resolution of missile-borne passive detector is figured out. The quantitative relationship between the resolution of detector and the geometric configuration of detection system is deduced by using bistatic ambiguity function and angular resolution function. The constraint of the geometric configuration relationship is reversely derived depending on the resolution requirements. Optimization principle of BDS satellite selection is then concluded. The simulated results verify the feasibility and effectiveness of the proposed optimization principle of BDS satellites selection.

radar engineering; BDS; missile-borne passive detector; resolution; selection principle

2016-12-06

航天一院高校联合创新基金项目(CALT201503)

肖泽龙(1978—), 教授, 博士生导师。E-mail:zelongxiao@mail.njust.edu.cn

TN958.97

A

1000-1093(2017)08-1555-08

10.3969/j.issn.1000-1093.2017.08.013