复杂装备轴承多重故障的线性判别分析与反向传播神经网络协作诊断方法

黄大荣, 陈长沙， 孙国玺， 赵玲， 米波

(1.重庆交通大学 信息科学与工程学院, 重庆 400074；2.广东石油化工学院 广东省石化装备故障诊断重点实验室， 广东 茂名 525000)

复杂装备轴承多重故障的线性判别分析与反向传播神经网络协作诊断方法

黄大荣1，2, 陈长沙1， 孙国玺2， 赵玲1， 米波1

(1.重庆交通大学 信息科学与工程学院, 重庆 400074；2.广东石油化工学院 广东省石化装备故障诊断重点实验室， 广东 茂名 525000)

由于复杂装备运行工作环境恶劣，导致其轴承多重故障诊断的准确率不高，为此提出一种基于线性判别分析(LDA)与反向传播(BP)神经网络协作下复杂装备轴承数据驱动的多重故障诊断方法。将无量纲指标作为轴承多重故障数据的反映指标，利用LDA对轴承多重故障的无量纲指标数据进行线性映射降维处理；通过拉格朗日极值法获得最佳投影向量，沿着该方向将轴承多重故障数据投影到类别最易区分的方向；将经投影处理后的样本作为BP神经网络的输入样本，通过训练测试网络，实现轴承多重故障的预测分类。对某型装备大型旋转机械机组进行仿真实验，验证了所提方法能够有效对轴承多重故障进行降维映射，并且能较好地实现多重故障分类诊断，具有良好的有效性和实用性。

机械学； 轴承多重故障诊断； 拉格朗日极值法； 线性判别分析； 反向传播神经网络

0 引言

随着工业的快速发展，工业大机组日趋大型化、高速化、复杂化，旋转机械等大型设备结构和工艺的复杂性，往往导致多重故障发生，多重故障特征相互混杂，呈现出多耦合、模糊性等特点，用传统的单一故障诊断方法无法解决，因此，多重故障诊断是一直难以突破的瓶颈难题。

复杂装备多重故障诊断可以通过分析机组内的轴承振动信号实现，目前国内外已有学者针对轴承故障诊断做了大量研究工作，研究方法主要分为：1)基于轴承故障机理的诊断方法[1-2]，通过对轴承运行机理进行分析，得到其故障状态和正常状态对应的响应信号特征，利用特征信号对轴承故障进行诊断；2)基于专家系统的轴承故障诊断方法[3-4]，通过搜集专家在轴承故障方面的大量经验和专业性知识，建立基于故障规则的专家库，通过故障推理对故障进行判别诊断；3)基于数据驱动的故障诊断方法[5-6]，通过监测机械设备运行的状态数据，对数据进行统计学习分析，建立基于数据驱动的故障诊断模型。由于轴承的振动机理复杂，难以建立精确的数学模型，同时由于目前欠缺轴承故障诊断的专家经验，难以获取足够的轴承故障诊断知识，专家轴承故障规则库的完备性不足。因此，本文采取线性判别分析(LDA)与反向传播(BP)神经网络协作下复杂装备轴承数据驱动的多重故障诊断方法，利用LDA进行故障数据处理，将反映故障的特征数据映射到特定的空间，以提高不同故障特征的区分能力，在此基础上，利用BP神经网络构建轴承多重故障诊断模型，识别故障类型。该方法主要解决轴承故障数据中的多重故障数据特征数据结构所导致的故障诊断识别精度不高问题，从而避免恶性设备损坏事故的发生，降低停机次数和缩短停机时间，减少工业经济损失。

1 LDA与BP神经网络协作下复杂装备轴承数据驱动的多重故障诊断模型

1.1 LDA轴承特征数据降维

在轴承数据中，常采用以下6个指标衡量轴承的运行状态，分别为：振动烈度、波形、脉冲、裕度、峰值和峭度。本文针对轴承原始特征数据中特征指标较多、样本数据量较大、对样本直接进行故障分类误差较大的缺陷，采用LDA方法将轴承数据进行降维，降维后不同类样本的分布区间及均值各不相同，有利于提高轴承数据的区分度。具体思路如下：1)将原始数据向最易进行分类的方向投影，实现降维；2)通过轴承样本数据类内散列矩阵和类间散列矩阵共同确定投影方向，保证投影方向的正确性。由于降维方向为故障数据更易分类的投影方向，故能有效提高后期BP神经网络故障诊断的准确率。

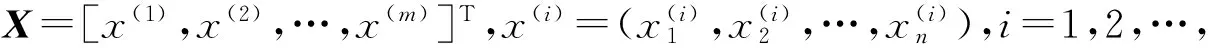
Y=Xm×nWn×1.

(1)

为找到最佳的降维投影向量Wn×1，设计如下算法结构：

1)假设轴承故障数据共有c个类别，第i类故障样本数有mi个，且满足

(2)

则对第i类故障样本Xi=(xij)mi×n定义的故障样本均值向量(Ui)1×n=(μ1,μ2,…,μn)，其中

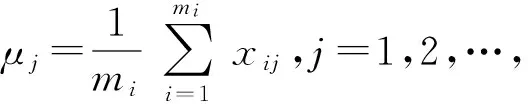
(3)

(4)

式中：wj为第j个指标对应的投影系数。

2)为衡量每个类中样本点的分布情况，引入一个度量值—散列值si，定义为

si=(Xi-U(i))T(Xi-U(i))，

(5)

式中：U(i)为(Ui)1×1按行按列扩展的mi×n矩阵；si为n×n散列矩阵，反映第i类所有样本点与该样本总体之间的关系。散列矩阵si的对角线元素是第i类所有样本点相对于该类总体的方差(即分散度)，非对角元素则是第i类样本所有样本点相对于该类总体均值的协方差(即该类和总体样本的相关关联度)。

令所有类样本点之间的分布散列值为Sw，即

(6)

(7)

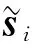
(8)

(9)

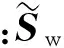
基于上述模型，定义样本总体各类样本点的散列规则为：

3)对于不同类之间的散列情形，定义类间离散度矩阵为

(10)

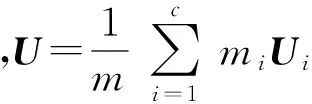
显然，某些类别样本点较多的情况下，相应的类与类之间的散列情况较紧密。

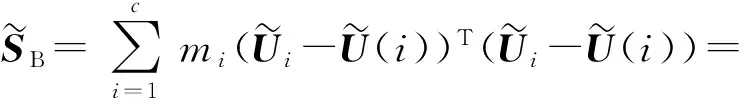
(11)

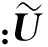
4) 根据前面所得到的类内样本散列值Sw和类间散列值SB，定义衡量样本点相对集中的度量模型为

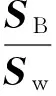
(12)

相应地，对应投影后的度量公式为

(13)

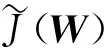
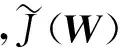
(14)

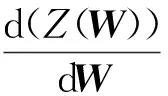
1.2BP神经网络轴承故障诊断

BP神经网络(见图1)是一种多层前馈神经网络，该网络的主要特点是信号前向传递、误差反向传播。在前向传递中，输入信号从输入层经隐含层逐层处理，直至输出层。每一层神经元的状态只影响下一层神经元的状态。如果输出层得不到期望的输出，则转入反向传播，根据预测误差调整网络权值和阈值，从而使BP神经网络的预测输出不断逼近期望输出[11]。

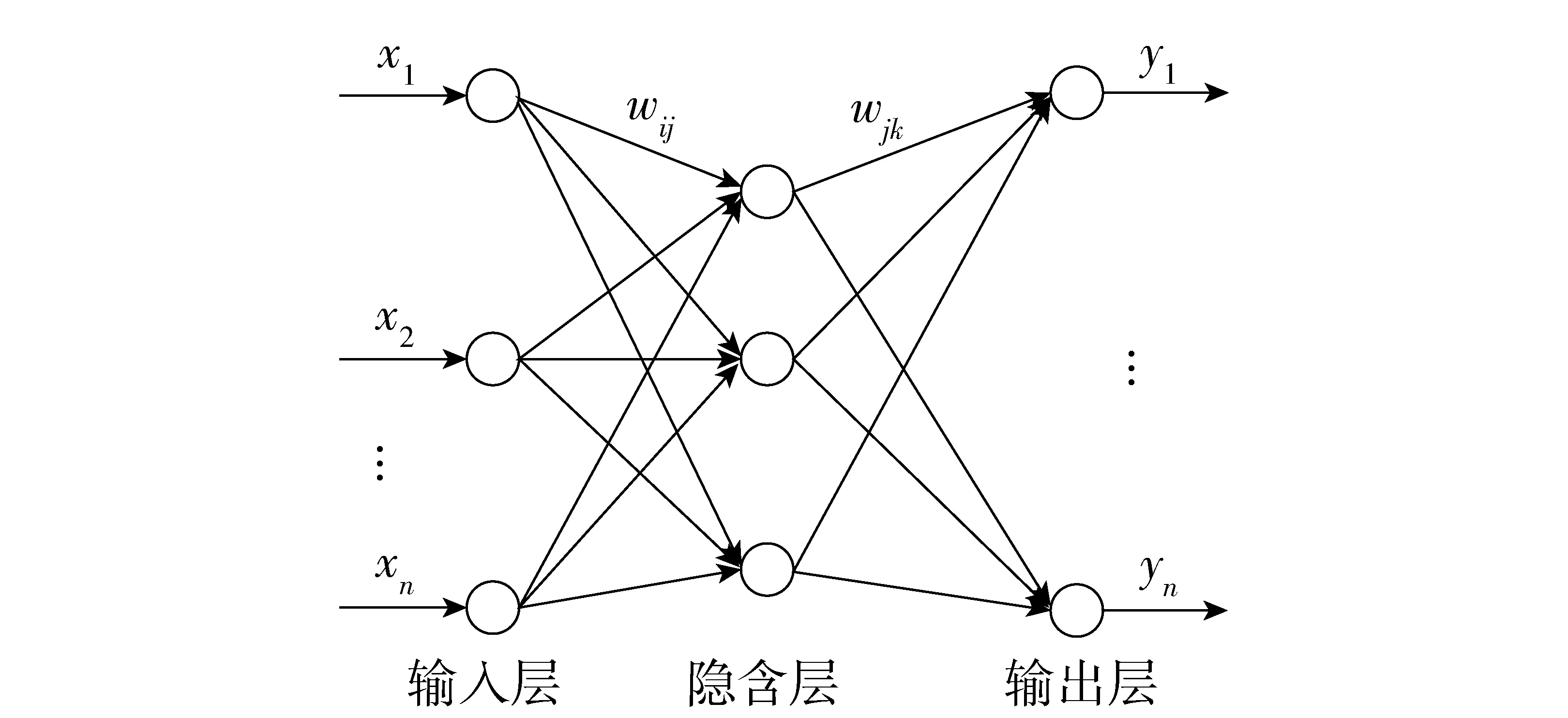
图1 BP神经网络拓扑结构图Fig.1 Topological structure of BP neural network

图1中，将经LDA降维后的轴承故障特征数据x1,x2,…,xn作为BP神经网络的输入值，轴承故障类别y1,y2,…,yn为BP神经网络的预测值，wij和wjk为权值。结合前面通过LDA降维后的轴承故障特征数据，可设计LDA与BP神经网络协作下复杂装备轴承多重故障诊断步骤如下：

1) 初始化神经网络参数；

2) 选择合适的隐含层函数；

3) 获得神经网络输出值；

4) 计算输出值与期望值之间的误差；

5) 根据误差进行权值更新；

6) 根据误差进行阈值更新；

7) 判断迭代误差是否小于阈值，若小于，则迭代结束，若不小于，则返回步骤2；

8) 利用训练好的神经网络进行故障诊断。

以上步骤迭代结束得到训练好的神经网络后，将测试样本输入该神经网络中，得到测试样本的输出值，该输出值即为BP神经网络的故障诊断结果；为了进一步研究该结果的可靠性，将该输出值与期望值进行比较，计算BP神经网络预测故障分类的准确率[12-15]。

2 仿真验证

2.1 LDA对iris特征数据降维

为了验证LDA方法降维的有效性，采用国际标准数据库UCI中的iris数据对该降维方法进行仿真，iris数据包含3个类，每个类分别有50个样本。该数据集由setosa、virginica和versicolor 3类植被数据组成，每类50个，共计150个样本，数据维度为4维，分别为萼片长度、宽度和花瓣的长度、宽度。为了验证LDA降维后数据类别区分度较好的性能，将iris数据进行LDA降维，观察降维后数据的分布。首先通过线性判别分析进行降维处理，根据(1)式～(13)式，得到对应特征值为

其对应的特征向量为

则最佳投影向量W=[0.230 2,-0.326 6,-0.347 2,0.848 4]T，得到投影向量Y150×1=X150×4W4×1，其中Y150×1包含3个类，每个类有50个样本，降维效果如图2所示。

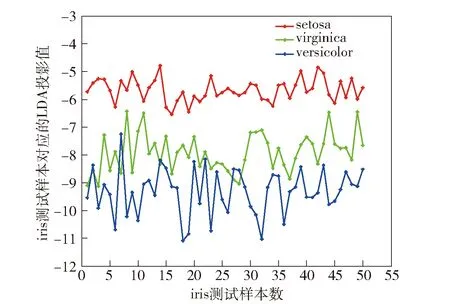
图2 iris数据经LDA投影后分布图Fig.2 Iris data after LDA projection

图2表明：投影后的同类向量之间基本在一个水平线上，且不同类之间的投影水平线各不相同；versicolor类中有个别样本点在viginica类范围内，表明这两个类中有几个样本点比较相似；通过对iris数据库中这两类样本的分析，发现在图中对应样本点处数据确实较接近。因此，LDA投影能保留数据本质特征并减少样本的维数。

2.2 BP神经网络预测分类

网络的输入为2.1节中得到的150个降维数据，其中105个作为训练样本，剩下45个作为测试样本；输入层、隐含层、输出层节点数分别设置为18、20、3；神经网络参数设置的训练次数为20 000，学习率为0.05，误差限为0.001，隐含层函数为sigmod函数，输出层为purelin函数，迭代方法采用有动量的梯度下降法，以提高学习速度，并增加算法的可靠性。预测分类效果如图3所示。

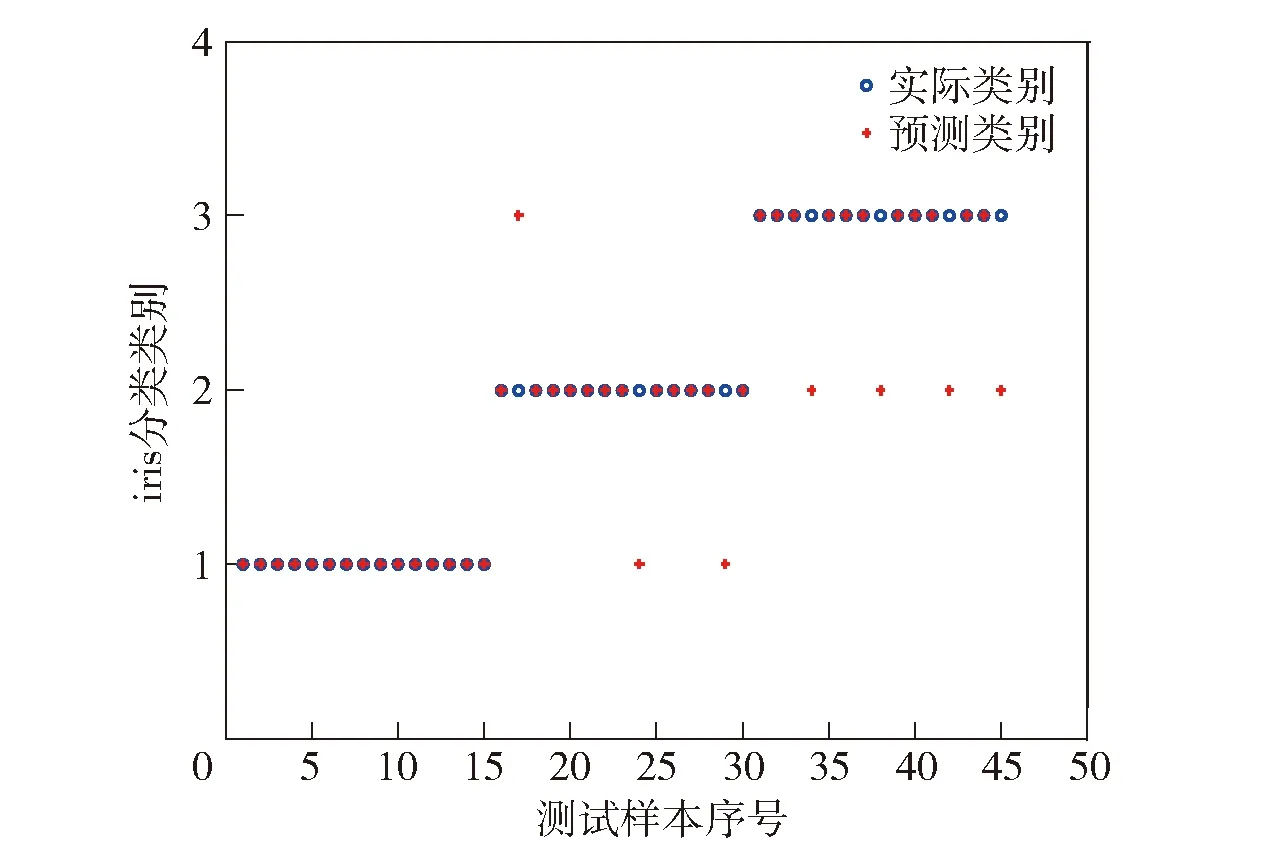
图3 LDA与BP神经网络协作下iris数据分类图Fig.3 Collaboration between LDA and BP neural network method to classify iris data

通过图3可以看出，LDA与BP神经网络协作分类方法能有效实现对iris数据的分类，分类准确率为84.44%. 仿真结果表明，LDA和BP神经网络协作对多重故障进行诊断在理论上是可行的。

3 LDA与BP神经网络协作下复杂装备轴承数据驱动的多重故障诊断实例仿真

为进一步验证本文所提出的模型和算法的有效性，将其应用到某型装备的轴承多重故障实际诊断中。仿真实验依托广东省石化装备故障诊断重点实验室平台，该平台以工业现场炼化装置大型旋转机械机组为参照，针对典型的工业机组结构和负载，结合大机组实验仿真装置，设计一套与系统匹配的故障配件，包括轴承外裂、轴承内裂、轴承滚珠磨损、轴承缺滚珠、裂齿、齿轮磨损等，实验故障配件如图4～图7所示。

图4 轴承滚珠磨损故障配件Fig.4 Wear fault parts of ball bearing

图5 轴承缺滚珠故障配件Fig.5 Fault parts of ball bearing

图6 裂齿故障配件Fig.6 Cracked tooth fault parts

图7 齿轮磨损故障配件Fig.7 Wear parts of gear

基于以上故障配件，实验选择NSK NN3021轴承型号进行多重故障仿真，并设计5类多重故障类型，分别为：类型1-正常，类型2-齿轮箱大小齿轮缺齿+左边轴承内圈缺滚珠，类型3-齿轮箱大小齿轮缺齿+右边轴承外圈磨损，类型4-齿轮箱大小齿轮缺齿+左边轴承内圈磨损，类型5-齿轮箱大小齿轮缺齿+左边轴承外圈磨损，其中，左边轴承表示位于负载左边的轴承，右边轴承表示位于负载右边的轴承。

仿真实验指标通常分为有量纲指标和无量纲指标。由于有量纲指标一般会随着石化装备工作条件(例如负载、转速、仪器灵敏度等)的改变而改变，反映出的故障类型不明显；而无量纲指标经两个有量纲指标比值得到，它对信号的幅值和频率变化不敏感，受复杂装备工作环境的影响不大，因此本次仿真采用无量纲指标作为故障类指标，分别为振动烈度、波形、脉冲、 裕度、峰值和峭度[16-20]。

3.1 LDA轴承特征数据降维

仿真数据包含以上5种类型共250个样本，每个故障类型样本数为50个，每个样本包含6个指标，分别针对上述仿真数据进行LDA降维，根据(1)式～(13)式，得出特征值为

对应的特征向量为

选用最大特征值对应的特征向量作为最佳投影向量，则W=[0.000 5,0.927 8,-0.223 4,-0.012 6,0.298 4,-0.007 5]T，于是轴承数据X250×6经LDA映射后为Y250×1=X250×6W6×1，即将一个含6个指标的样本点降维为一维的，对应的仿真图如图8所示。

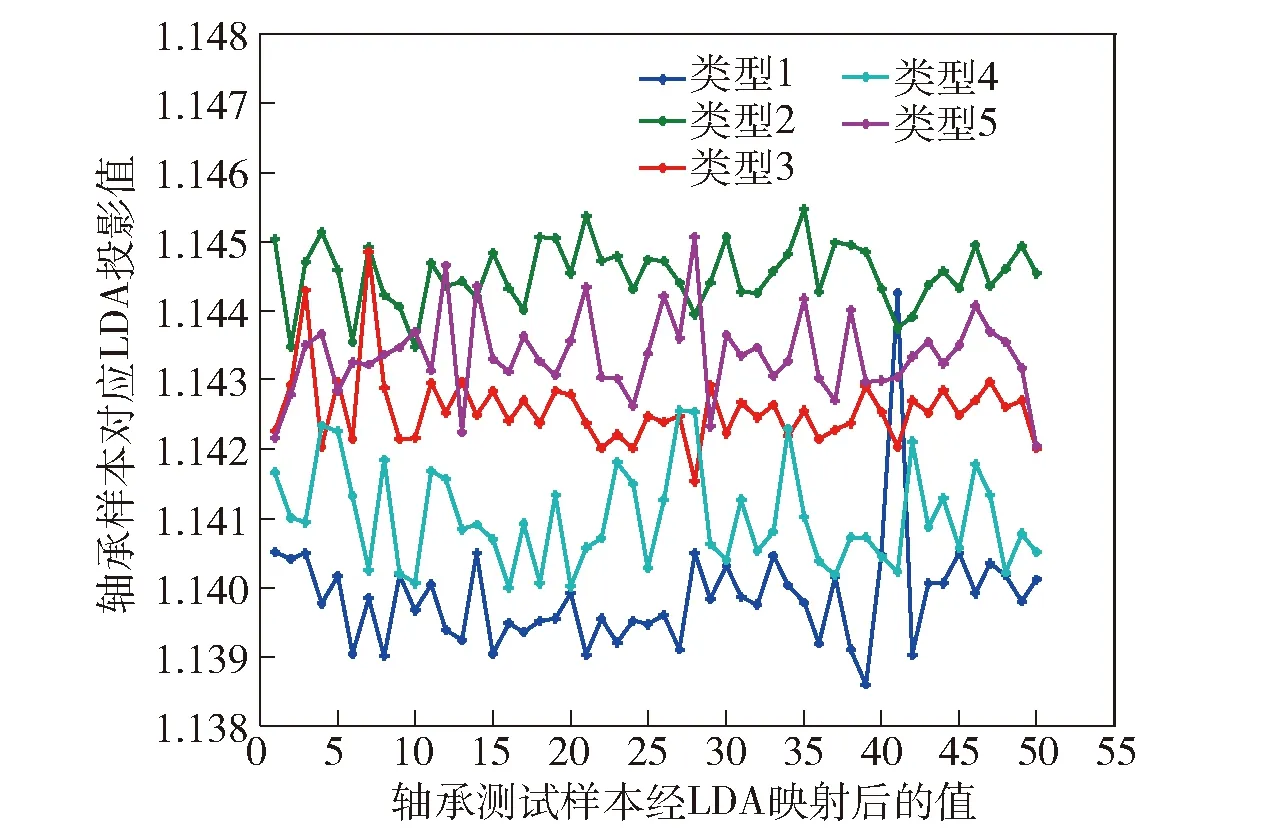
图8 轴承测试样本经LDA映射后分布图Fig.8 Distribution of bearing testing samples after LDA projection

从图8中可以看出：在轴承故障类型中，类型1即正常情况运行时，其LDA映射幅值与发生故障后的4个类型相比其值较小；在发生的4种故障类型中，类型2即齿轮箱大小齿轮缺齿+左边轴承内圈缺滚珠的幅值较大，这是由于轴承缺滚珠时，其运行状态极其不稳定，总体无量纲指标值偏大导致的；类型3和类型5较接近，表明故障类型即齿轮箱大小齿轮缺齿+右边轴承外圈磨损的无量纲指标值不受故障出现位置因素的影响；类型4即齿轮箱大小齿轮缺齿+左边轴承内圈磨损与正常情况无量纲指标值较接近，因此其LDA映射值也较相近。综上所述，该实验结果与实际情况基本相符，表明采用LDA方法进行多重故障无量纲指标数据降维处理是有效的。

3.2 BP神经网络轴承故障诊断

将降维后数据Y250×1作为BP神经网络的输入，每个类型故障数据35个作为训练数据，输入层、隐含层、输出层节点数分别设置为20、24、5；另外15个作为训练数据，因此本次BP仿真训练数据共175个样本点，75个测试点，神经网络参数设置的训练次数为20 000，学习率为0.05，误差限为0.001.

通过数据拟合得到故障分类效果如图9所示。

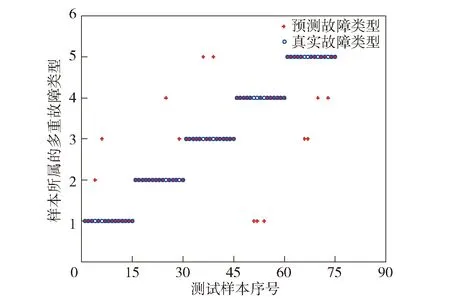
图9 LDA与BP神经网络协作下复杂装备轴承多重故障分类效果图Fig.9 Collaboration between LDA and BP neural network method to classify bearing data

显然，LDA与BP神经网络协作下复杂装备轴承多重故障诊断的准确率较高，为82.67%，对应均方误差曲线如图10所示。

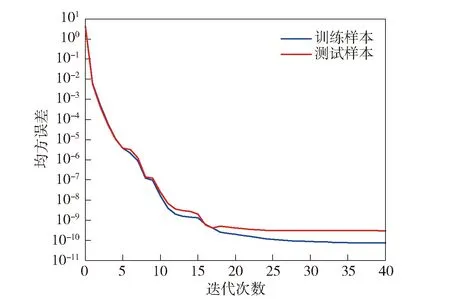
图10 LDA与BP神经网络协作下复杂装备轴承多重故障分类误差曲线图Fig.10 Error curves of bearing multi-fault classification of LDA and BP neural network

图10表明，LDA与BP神经网络协作下故障诊断的误差率很小。

为进一步验证本文方法的合理性，将该方法与直接进行BP神经网络轴承多重故障分类的方法进行比较，对采集到的轴承多重故障数据X250×6直接进行BP神经网络故障分类，分类效果如图11所示。

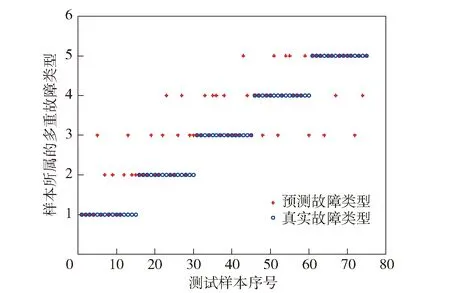
图11 BP神经网络预测分类效果图Fig.11 Predictive classification effect chart of BP neural network

对比图9和图11可知，直接利用BP神经网络进行分类的正确率为58.6%，远远低于LDA与BP神经网络协作下轴承多重故障诊断方法的准确率，原因是轴承多重故障无量纲指标数据之间存在较强的耦合性，如果未进行前期LDA映射降低耦合的处理，就直接利用BP神经网络进行故障分类，其得到的故障分类准确率会比较低。综上所述，本文提出的LDA与BP神经网络协作下复杂装备轴承数据驱动的多重故障诊断效果较好，能对复杂装备多重故障进行有效分类诊断。

4 结论

1)针对复杂装备轴承多重故障难以区分的问题，提出利用LDA对轴承多重故障数据进行线性判别降维处理，将故障数据向最易区分的方向投影，有效提高了轴承多重故障的诊断准确度。

2)引入无量纲指标对复杂装备多重故障进行了研究分析，将得到的无量纲指标数据作为轴承多重故障的特征指标。

3)在结论1、结论2的基础上，利用BP神经网络构建了轴承多重故障无量纲指标与故障类型之间的非线性函数模型。仿真结果表明，LDA与BP神经网络协作下复杂装备轴承数据驱动的多重故障诊断方法能较好地克服复杂装备轴承原始特征数据中特征指标较多、样本数据量较大、对样本直接进行多重故障分类误差较大等缺点，是一种有效的故障诊断方法。

本文方法有效解决了多重故障样本与样本间的区分，但是并未解决多重故障样本内部故障的区分，如何提高多重故障样本内故障的区分准确率是复杂装备行业极其关心的问题，有待进一步研究解决，本文作者目前正在开展这方面的研究工作，限于篇幅，将另文给出。

References)

[1] 崔玲丽, 张宇, 巩向阳, 等. 基于振动响应机理的轴承故障定量诊断及量化分析[J]. 北京工业大学学报, 2015, 41(11):1681-1687. CUI Ling-li, ZHANG Yu, GONG Xiang-yang, et al. Vibration mechanism based quantitative diagnosis and quantization analysis of rolling bearing fault[J]. Journal of Beijing University of Technology, 2015, 41(11):1681-1687. (in Chinese)

[2] 石双平. 滚动轴承故障诊断机理研究[J].机械设计与制造, 2014(10):236-239. SHI Shuang-ping. Mechanism of rolling bearings fault diagnosis[J]. Machinery Design & Manufacture, 2014(10):236-239. (in Chinese)

[3] Saimurugan M, Ramachandran K I, Sugumaran V. Multi component fault diagnosis of rotational mechanical system based on decision tree and support vector machine[J]. Expert Systems with Application, 2011, 38(4):3819-3826.

[4] Prasad G D, Kumar B R, Ramana K V. Development of an expert system for diagnosis of bearing faults of rotating machinery with a case study on boiler feed pump[J]. International Journal of Current Research & Review, 2012, 4(7):16-18.

[5] Li B, Chow M Y, Tipsuwan Y, et al. Neural-network-based motor rolling bearing fault diagnosis[J]. IEEE Transactions on Industrial Electronics, 2000, 47(5):1060-1069.

[6] 王新峰, 邱静, 刘冠军. 基于绕封模型的故障特征选择方法研究[J]. 兵工学报, 2005, 26(5):685-689. WANG Xin-feng, QIU Jing, LIU Guan-jun. Research on fault feature selection methods based on the sealing model[J]. Acta Armamentarii, 2005, 26(5):685-689.(in Chinese)

[7] 张锐戈, 谭永红. 双谱主成分分析的滚动轴承智能故障诊断[J]. 振动工程学报, 2014, 27(5) :763-769. ZHANG Rui-ge, TAN Yong-hong. Intelligent fault diagnosis of rolling element bearing based on bispectrum principal components analysis[J]. Journal of Vibration Engineering, 2014, 27(5):763-769.(in Chinese)

[8] 程静, 王维庆, 何山. 双谱分析法在风机轴承故障诊断中的应用[J]. 自动化仪表, 2016, 37(7):27-29. CHENG Jing, WANG Wei-qing, HE Shan. Application of the dual spectrum analysis method in fault diagnosis of wind turbine bearing[J]. Process Automation Instrumentation, 2016, 37(7):27-29.(in Chinese)

[9] 郝腾飞, 陈果, 廖仲坤. 基于正则化多核判别分析的航空发动机滚动轴承早期故障融合诊断方法[J]. 航空动力学报, 2013, 28(12):2759-2770. HAO Teng-fei, CHEN Guo, LIAO Zhong-kun. Approach for incipient fusion fault diagnosis of rolling bearing of aero-engine based on regularized multiple kernel discriminant analysis[J]. Journal of Aerospace Power, 2013, 28(12):2759-2770.(in Chinese)

[10] 杨杰, 郑海起, 关贞珍. 基于形态成分分析的轴承复合故障诊断[J]. 轴承, 2011(8):38-42. YANG Jie, ZHENG Hai-qi, GUAN Zhen-zhen. Compound fault diagnosis for bearings based on morphological component analysis[J]. Bearing, 2011(8):38-42.(in Chinese)

[11] 杨宇, 于德介, 程军圣. 基于Hilbert边际谱滚动轴承故障诊断方法[J]. 振动与冲击, 2005, 24(1):70-72. YANG Yu, YU De-jie, CHENG Jun-sheng. Roller bearing fault diagnosis based on Hilbert marginal spectrum[J]. Journal of Vibration and Shock, 2005, 24(1):70-72.(in Chinese)

[12] 梁峰, 张丹丹, 张荣华. 基于BP神经网络的水润滑艉轴承故障诊断研究[J]. 机械传动, 2015, 39(7):118-121. LIANG Feng, ZHANG Dan-dan, ZHANG Rong-hua. Fault diagnosis of water lubricated stern bearing based on BP neural network[J]. Journal of Mechanical Transmission, 2015, 39(7):118-121.(in Chinese)

[13] 赵刚, 黄大荣, 黄席樾. 火箭漏电故障诊断技术研究[J].兵工学报, 2010, 31(7):916-921. ZHAO Gang, HUANG Da-rong, HUANG Xi-yue. Research on the leak current fault diagnosis technology for launch vehicle[J]. Acta Armamentarii, 2010, 31(7):916-921.(in Chinese)

[14] 梁传建, 杨国来, 王晓锋. 基于神经网络和遗传算法的火炮结构动力学优化[J]. 兵工学报, 2015, 36(5):789-794. LIANG Chuan-jian, YANG Guo-lai, WANG Xiao-feng. Structural dynamics optimization of gun based on neural networks and genetic algorithms[J]. Acta Armamentarii, 2015, 36(5):789-794.(in Chinese)

[15] 张可, 柴毅, 刘建环. 一类基于类别区分的多重故障诊断模型框架[J]. 控制理论与应用, 2016, 33(2):154-163. ZHANG Ke, CHAI Yi, LIU Jian-huan. A class of category discrimination based model frameworks for multiple fault diagnosis[J]. Control Theory & Applications, 2016, 33(2):154-163.(in Chinese)

[16] 张清华, 邵龙秋, 李红芳. 基于无量纲指标的旋转机械并发故障诊断技术[J]. 华中科技大学学报:自然科学版, 2009, 37(增刊1):156-159. ZHANG Qing-hua,SHAO Long-qiu,LI Hong-fang.Research of concurrent fault diagnosis technology of rotating machinery based on the non-dimensional parameter[J]. Journal of Huazhong University of Science and Technology: Natural Science,2009, 37(S1):156-159. (in Chinese)

[17] 李志农, 朱明.基于变分模态分解的机械故障诊断方法研究[J].兵工学报,2017,38(3):593-599. LI Zhi-nong,ZHU Ming.Research on mechanical fault diagnosis method based on variational mode decomposition[J]. Acta Armamentarii, 2017,38(3):593-599. (in Chinese)

[18] 程昊宇, 董朝阳, 江未来,等.变体飞行器故障检测与容错控制一体化设计[J].兵工学报,2017,38(4):711-721. CHENG Hao-yu,DONG Chao-yang,JIANG Wei-lai,et al.Integrated fault diagnosis and fault tolerant control for morphing aircraft[J].Acta Armamentarii,2017,38(4):711-721. (in Chinese)

[19] 李海广，潘宏侠，任海锋.基于冲击响应谱特征提取的自动机裂纹故障诊断[J].兵工学报2016,37(9):1744-1752. LI Hai-guang,PAN Hong-xia,REN Hai-feng.Crack fault diagnosis of automatic mechanism based on shock response spectrum features extraction[J]. Acta Armamentarii, 2016,37(9):1744-1752. (in Chinese)

[20] 田恒，段富海，江秀红，等.基于准信息熵的测试性D矩阵故障诊断新算法[J].兵工学报，2016,37(5):923-928. TIAN Heng,DUAN Fu-hai,JIANG Xiu-hong,et al.A novel fault diagnosis algorithm of testability D matrix based on quasi information entropy[J]. Acta Armamentarii, 2016,37(5):923-928. (in Chinese)

Linear Discriminant Analysis and Back Propagation Neural Network Cooperative Diagnosis Method for Multiple Faults of Complex Equipment Bearings

HUANG Da-rong1,2, CHEN Chang-sha1, SUN Guo-xi2, ZHAO Ling1，MI Bo1

(1.College of Information Science and Engineering, Chongqing Jiaotong University, Chongqing 400074, China;2.Guangdong Provincial Key Laboratory of Petrochemical Equipment Fault Diagnosis, Guangdong University of Petrochemical Technology, Maoming 525000, Guangdong , China)

The fault diagnosis accuracy of bearing for complex equipment is not high due to the structural complexity of complex equipment and the poor working environment. A method of multiple bearing fault diagnosis based on linear discriminant analysis (LDA) and BP neural network is presented. A linear discriminant analysis is utilized for the linear dimension reduction of the dimensionless bearing multiple fault index, which is taken as an indicator of fault data. Lagrange extremum method is used to obtain an optimal projection vector. The bearing multiple fault data is projected on a category most likely to distinguished direction. The projected samples are used as the input samples of BP neural network and the test network. The simulation experiment of a certain large rotating machinery units shows that the proposed method can effectively reduce the dimensional mapping of multi-fault, achieve better classification, and has good validity and practicability.

mechanics; bearing multiple fault diagnosis; Lagrangian extremum method; linear discriminant analysis; BP neural network

2016-12-02

国家自然科学基金项目(61663008、61573076、61473094、61304104、61004118)；教育部留学归国人员科研启动基金项目(2015-49);重庆市高等学校优秀人才支持计划项目(2014-18)；广东省石化装备故障诊断重点实验室开放式基金项目(GDUPKLAB201501、GDUPKLAB201604)；重庆市研究生教育教学改革研究重点项目(yjg152011)；重庆市高等教育学会2015—2016高等教育科学研究课题项目(CQGJ15010C)

黄大荣(1978—)，男，教授，硕士生导师。E-mail：hcx1978@163.com

TH133.33+1

A

1000-1093(2017)08-1649-09

10.3969/j.issn.1000-1093.2017.08.024