基于压缩感知的辐射源信号数据级融合识别方法

王志鹏， 王星， 田元荣， 周一鹏

(空军工程大学 航空航天工程学院， 陕西 西安 710038)

基于压缩感知的辐射源信号数据级融合识别方法

王志鹏， 王星， 田元荣， 周一鹏

(空军工程大学 航空航天工程学院， 陕西 西安 710038)

针对协同侦察数据级融合识别中通信量大的问题，利用压缩感知可用少量测量值表征完整信号的特点，提出了一种基于压缩感知的数据级融合识别方法。接收终端采用确定测量阵对侦察信号的Gabor时频特征进行压缩测量，通过传输少量的压缩测量值以减轻通信压力，融合中心根据多源测量数据间的相关特性，采取相关性融合规则直接对多源压缩测量数据进行融合，最后再计算融合压缩测量值在不同类信号字典下的重构误差，最小重构误差对应的信号类别即识别结果。分别对融合识别方法识别性能和相关性融合规则融合效果进行仿真分析，实验结果表明：所提方法在保证识别率的同时大幅减小了数据通信代价，在低信噪比时识别性能突出、抗噪声干扰性能好；相比于其他融合规则，基于测量向量相关性的融合规则可保留更为全面的信息。

兵器科学与技术； 辐射源识别； 数据级融合； 压缩感知； 时频变换； 相关性融合规则

0 引言

辐射源信号识别是电子侦察的一个关键内容。传统的电子侦察采用单平台的方式，单平台在空间位置、截获性能和处理能力等方面存在局限[1]。同时，电子侦察的对象为非合作信号，当受环境影响或接收机与目标辐射源信号主瓣未对准时，接收脉冲容易产生缺失或畸变[2]。这些使得接收信号具有较大的不确定性和不完整性，导致基于单平台的辐射源信号识别性能不佳。而多平台协同侦察通过对多源信息进行融合，不同信息互补，相同信息映证增强，可形成目标辐射源更为准确全面的信息，提升识别性能[3]。

根据融合系统中数据抽象的层次，信息融合可分为数据级融合、特征级融合和决策级融合[4]。特征级融合识别[5-6]和决策级融合识别[7-8]先由单平台独立对辐射源信号进行大量处理，分别获得辐射源脉冲描述字(PDW)等特征参数和单平台识别结果，然后再进行时域和空域的融合，这两种方法对通信量要求不高，具有较好的实时性，但无法处理上述的脉冲缺失情况，大量底层有用信息丢失，会影响侦察识别效果。数据级融合识别可以较完整地保留底层有用信息，实现对目标辐射源信号的准确侦察识别，但数据级融合的数据处理量和通信量大，目前研究较少。文献[9]提出一种基于多分辨率分析的雷达信号数据级融合算法(MT算法)，该算法提高了信息的利用率，但MT算法对二维小波系数进行融合，通信量非常大；文献[2]提出的基于稀疏表示的数据级融合识别算法(SRSF算法)通过减少稀疏字典原子个数以减小稀疏向量长度，虽然能在一定程度上减小数据通信量，但对信号恢复精度有很大影响，最终影响信号识别率。

压缩感知(CS)技术是一种新兴的信号采样处理技术，其核心思想是将高维信号线性投影到低维空间，通过求解欠定线性系统最优化，以高精度从低维投影信号中恢复原始信号[10]。由于其能以远低于奈奎斯特频率的采样速度对信息进行采样和以较少的比特数表示信号，目前被广泛用于核磁共振、无线传感网络、成像雷达等数据量大的领域，这也为辐射源信号数据级融合提供了可能。

基于此，本文将压缩感知理论引入辐射源信号数据级融合，建立了基于CS的辐射源信号数据级融合识别模型。首先对接收信号进行Gabor变换，提取信号时频特征；然后采用高斯随机阵对时频阵进行压缩测量，传输少量测量向量，以减小通信代价；多源测量值在融合中心汇总后，采取相关性融合规则直接在测量域进行融合；通过计算融合后测量值在不同类信号字典下的重构误差识别信号类型。仿真结果验证了本文所提方法的可行性与有效性。

1 压缩感知

图1为CS数学模型的示意图，原始信号x∈Rn×1，存在一个字典矩阵D(D∈Rn×l，l≥n)，在D下x可用一个稀疏向量s(s∈Rl×1)表示，s中包含k个非零项，k为稀疏向量s的稀疏度。利用测量矩阵Φ(Φ∈Rm×n)对原始信号x进行测量，获得测量信号y(y∈Rm×1)，其中m≪n，Θ=ΦD称为恢复矩阵。

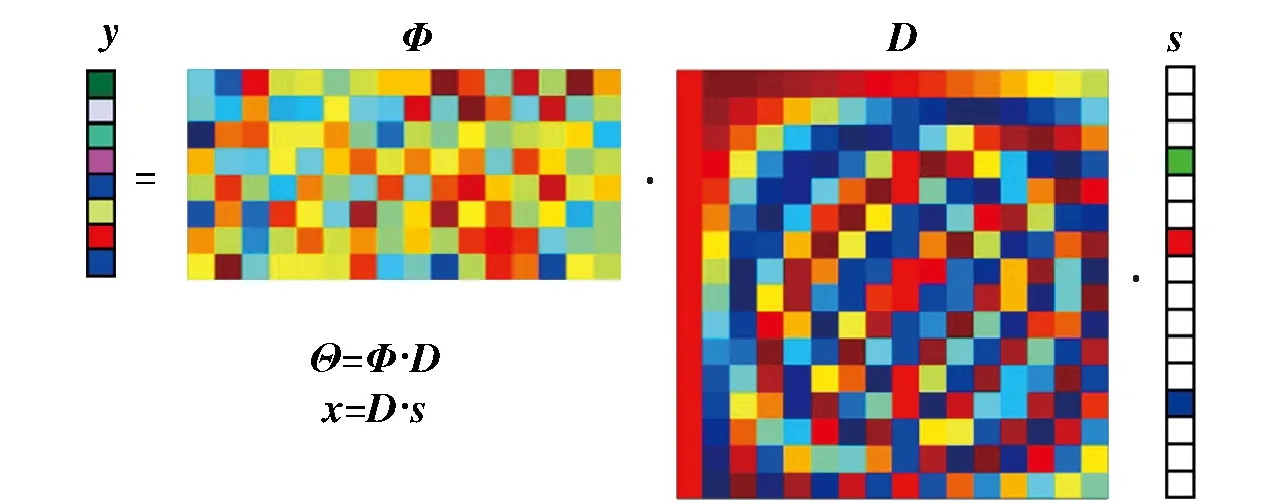
图1 压缩感知数学模型Fig.1 Mathematic model of compressed sensing

CS主要包括两部分内容，原始信号的稀疏性和信号重构[11]。自然界中大部分信号均存在一个合适的字典矩阵，使得信号具有稀疏特性，即x∈Rn×1，x=Ds，s为一稀疏信号。在重构过程中，方程组y=Θs描述为一个欠定线性系统，若测量向量y在恢复矩阵Θ列向量的张成空间中，则系统有无穷解。为缩小解的范围，对该欠定线性系统进行正则化，引入评价函数J(s)，取J0(s)=‖s‖l0，可以得到稀疏解s0. 对欠定线性系统求稀疏解转变为最优化问题(PJ0)：在线性方程组的解集s中寻找一个最优解s0，使s0中非0元素最少，即稀疏解。

(PJ0):s0=min ‖s‖l0, s.t.y=Θs.

(1)

由于(PJ0)为NP-Hard问题，根据l0范数和l1范数的等价性，令J1(s)=‖s‖l1，(PJ0)转变为(PJ1)，

s0=min ‖s‖l1, s.t.y=Θs.

(2)

(PJ1)问题可通过最小l1范数法、匹配追踪系列算法、迭代阈值法等方法求解，本文采用正交匹配追踪(OMP)算法。

稀疏性和约束等距性(RIP)，或者稀疏性和非相干性，是CS中原始信号能否由测量值精确重构的两个基本原则。目前，用于信号稀疏分解的稀疏字典有正交基字典、框架字典和冗余字典等，由于辐射源信号样式复杂，本文采用K-SVD学习的方法构造稀疏冗余字典。

研究表明，当随机测量阵Φ的维度满足：

m≥Cklg (n/k),

(3)

式中：C为某固定常数[12]。对于任意的正交字典D和测量阵Φ能很大概率地满足RIP. 独立同分布的高斯随机变量形成的测量矩阵与任意正交字典都具有较强的不相关性[13]，因此本文选择高斯随机测量矩阵。

2 基于压缩感知的雷达信号数据级融合识别

2.1 基于Gabor变换的信号时频特征提取

传统雷达信号分析大多数都是基于时域或者频域，这样对于频点单一或变化不多的信号分析效果较好，但随着现代雷达信号调制方式不断发展，时变性和非平稳性成为现代雷达信号的显著特点，传统的雷达信号分析方式无法表征信号的局部时变特征。时频分析作为分析时变非平稳信号的有力工具，能较好地反映雷达信号能量随频率和时间变化的局部特征。本文采用Gabor变换的方法，提取信号时频特征[14]。选用线性调频(LFM)信号进行时频分析，脉宽为10 μs，带宽为10 MHz，中心频率5 MHz，采样频率30 MHz，图2为信号无噪和信噪比0 dB情况下的Gabor变换时频图。

图2 LFM信号的Gabor变换时频图Fig.2 Gabor transform of LFM signal

从图2(a)可以看出，信号经过Gabor变换，信号与背景边界清晰，能量比较聚集，时频特征明显。图2(b)中当信噪比0 dB时，由于加入白噪声，噪声分量在时频图内杂乱分布，但主体的LFM信号时频特征仍然比较清晰，Gabor时频变换具有较好的抗噪性能。

缺失干扰是影响侦察效果的一个重要因素，本文简单定义缺失率η，从时域定量描述缺失干扰，Tj为一个脉冲内缺失干扰的时间，Tp为脉宽。

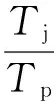
(4)

对脉冲串信号进行时频分析，脉冲串包含4个脉冲，占空比为50%，脉内调制参数与图1(a)的参数相同, 缺失率η=0.4，信号Gabor时频图如图3所示。

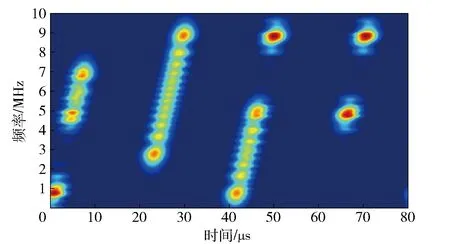
图3 η=0.4时脉冲串信号的时频图Fig.3 Gabor transform of pulse string signal for η=0.4

2.2 基于压缩感知的融合识别算法

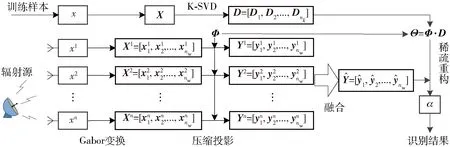
图4 基于压缩感知的辐射源信号融合识别模型Fig.4 Emitter signal fusion identification process based on compressed sensing

本文在时间配准和归一化的基础上进行。输入信号一部分是标准的训练样本信号，训练离线稀疏字典库，用于匹配识别，另一部分是接收机接收的辐射源信号作为测试样本，信号处理流程如图4所示。样本信号经过Gabor变换后，采用K-SVD算法训练离线稀疏字典库，稀疏字典与测量矩阵构成恢复矩阵，用于测试信号的分类识别；测试信号经过Gabor变换后形成时频特征矩阵，由于雷达信号的密集特征和时频阵的高维数特性，为减小测试信号在融合传输过程中的通信量，对时频向量组进行压缩投影，测量矩阵取高斯随机矩阵，多源测量值采用相关融合算法进行融合，融合后的测量向量在恢复矩阵下，利用OMP算法重构原始信号的稀疏系数，并计算其残差，残差最小的类即识别的信号类型。

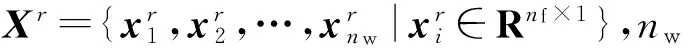
为确保压缩采样能保留原始信号的完备信息，采用高斯随机测量矩阵Φ∈Rnp×nf对时频阵进行压缩投影，Φ中每个元素独立地服从均值为0，方差为1/np的正态分布，且np≪nf，np满足(3)式约束。

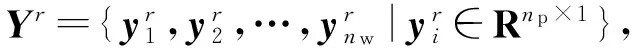
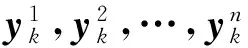
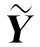
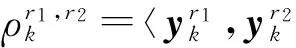
(5)

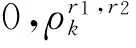
(6)

(7)

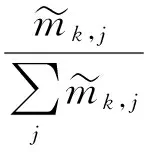
(8)

融合后的测量向量

(9)

每类信号可产生多个，作为样本信号输入，训练稀疏离线字典库，第j类信号xj经过Gabor变换后，利用K-SVD算法训练得到j类信号的离线字典Dj={d1,j,d2,j,…,dnd,j|di,j∈Rnf×1}，每类信号依次构建离线字典，最终得到字典库D={D1,D2,…,Dnk|Dj∈Rnf×nd}，nk为训练样本类别总数。

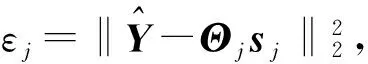
(10)

式中：Θj为字典Dj与测量矩阵Φ构成对应的恢复矩阵；sj为恢复矩阵Θj下的稀疏向量；εj为重构误差；k为稀疏度，即迭代次数。

拥有最小重构误差的字典对应的信号类别即为识别结果:

(11)

算法流程如图5所示。

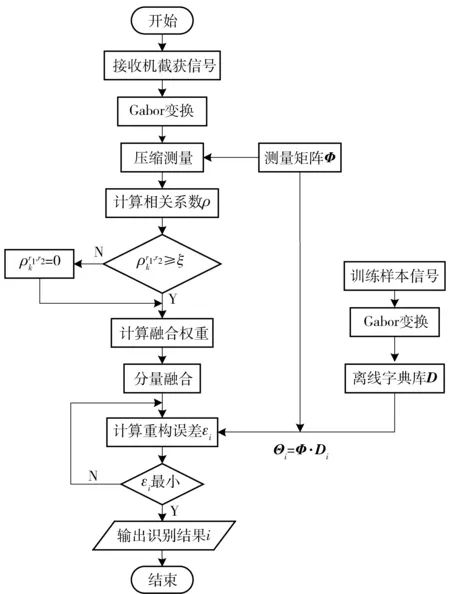
图5 压缩感知融合识别算法流程图Fig.5 Flow chart of compressed sensing-based fusion identification algorithm

3 仿真实验

3.1 融合效果

仿真参数选用机载火控雷达有源跟踪模式典型波形参数[15]，目标雷达发射脉冲脉宽为5 μs，占空比为25%，测试发射脉冲串包含4个脉冲，脉内调制样式为LFM，信号中心频率为5 MHz，带宽为8 MHz，采样频率为30 MHz. 训练样本脉冲串包含1个完整脉冲，可能的雷达信号调制样式有LFM、非线性余弦调频(NCFM)、频率调制(BFSK、QFSK)和相位编码(BPSK和QPSK)，其中BPSK和BFSK信号采用长度为7的巴克码，QPSK和QFSK采用16位弗兰克码。

由于信道噪声和缺失干扰，对测试发射信号加入信噪比为[5 dB, 10 dB]的高斯白噪声，和缺失概率η为[0, 0.6]的随机缺失干扰，3个不同平台的电子侦察接收机的接收信号分别为x1(k)，x2(k)，x3(k).

根据2.2节中提出的基于CS的辐射源信号融合识别模型，接收机对测试信号进行采样，xn(k)采样长度为2 400点，然后对采样信号进行Gabor变换，变换帧长100点，帧间重叠25点，经过Gabor变换后时频阵Xn为199×32，3个接收机信号的时域图和Gabor变换时频图见图6. 根据(3)式及字典训练情况选择高斯随机阵维度为10×199，经过压缩投影后测量向量集为10×32，相关融合中，根据实验经验数据，相关度阈值ξ设为0.34。训练样本信号的时频阵为199×7。每类信号选取100个样本，经过K-SVD训练后，冗余字典Dj包含200个原子，经过相关融合算法后，利用OMP算法对信号进行重构，设定迭代次数为10.

为了直观反映融合识别效果，对融合后的投影时频阵信号进行重构(实际应用中，不需要进行信号重构)，重构信号如图7所示。对比图6和图7可知：虽然接收信号存在不同程度的缺失，但经过相关融合，不同源信号可实现较好的互补，在时频域形成完整信号，而且时频图中杂乱分布的噪声分量减少，这对于提高残缺信号利用率和信号的识别率具有重要作用。因此，基于测量向量相关性的融合方法是有效的，并且具有一定的抗噪效果。

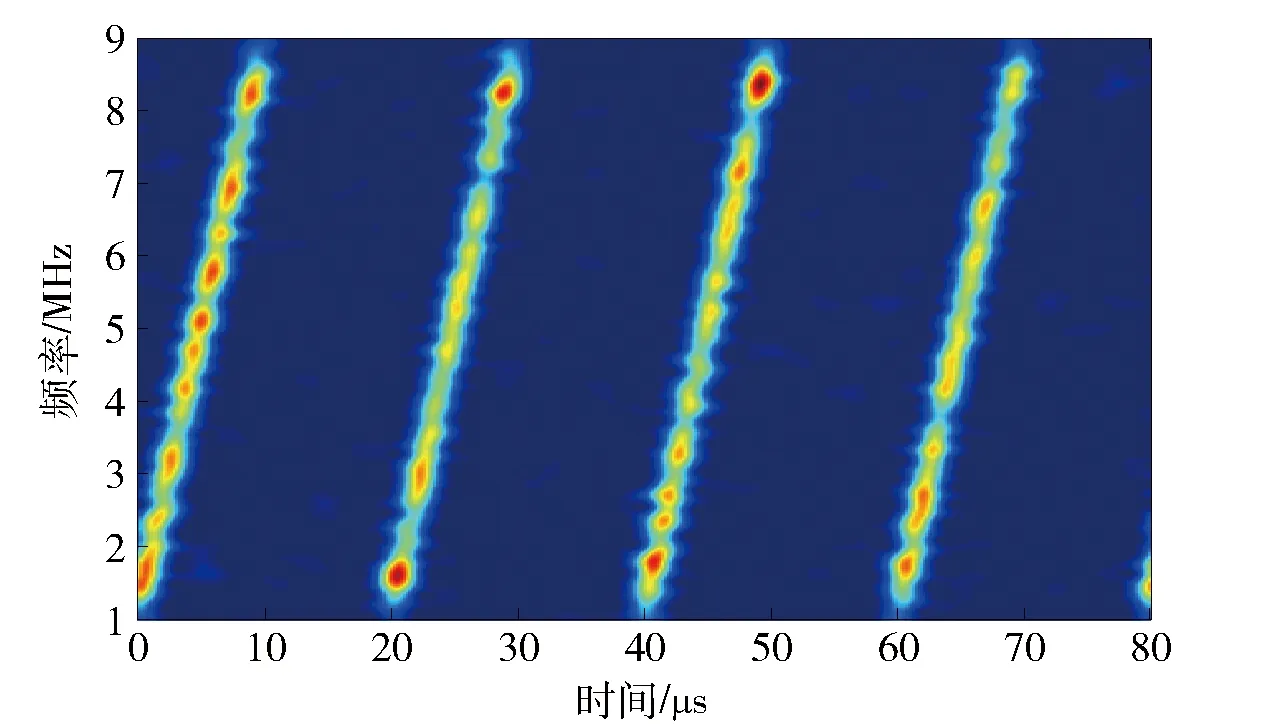
图7 相关融合后重构信号Fig.7 Reconstructed signal after correlation fusion

3.2 算法识别性能

为对比不同数据级融合识别算法的性能，如图8所示，将文献[9]中的MT算法、文献[2]中的SRSF算法和本文提出的基于CS的相关融合识别算法进行对比，分析其通信量和识别性能，识别性能用识别率ζ来描述：

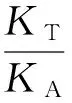
(12)

式中：KT为正确识别样本数；KA为待测试样本总数。

缺失率η=0.3，信道噪声信噪比在[-5 dB, 12 dB]变化，其他仿真参数设置与3.1节相同，单次实验中不同融合识别算法使用的信号相同。MT方法中分块矩阵大小为8×8，小波分解函数使用Mexh函数，系数向量求解利用Matlab提供的dwt2函数。SRSF分块矩阵大小为8×8，K-SVD训练的冗余字典有64个原子。相关融合算法中高斯随机阵维度为10×199.

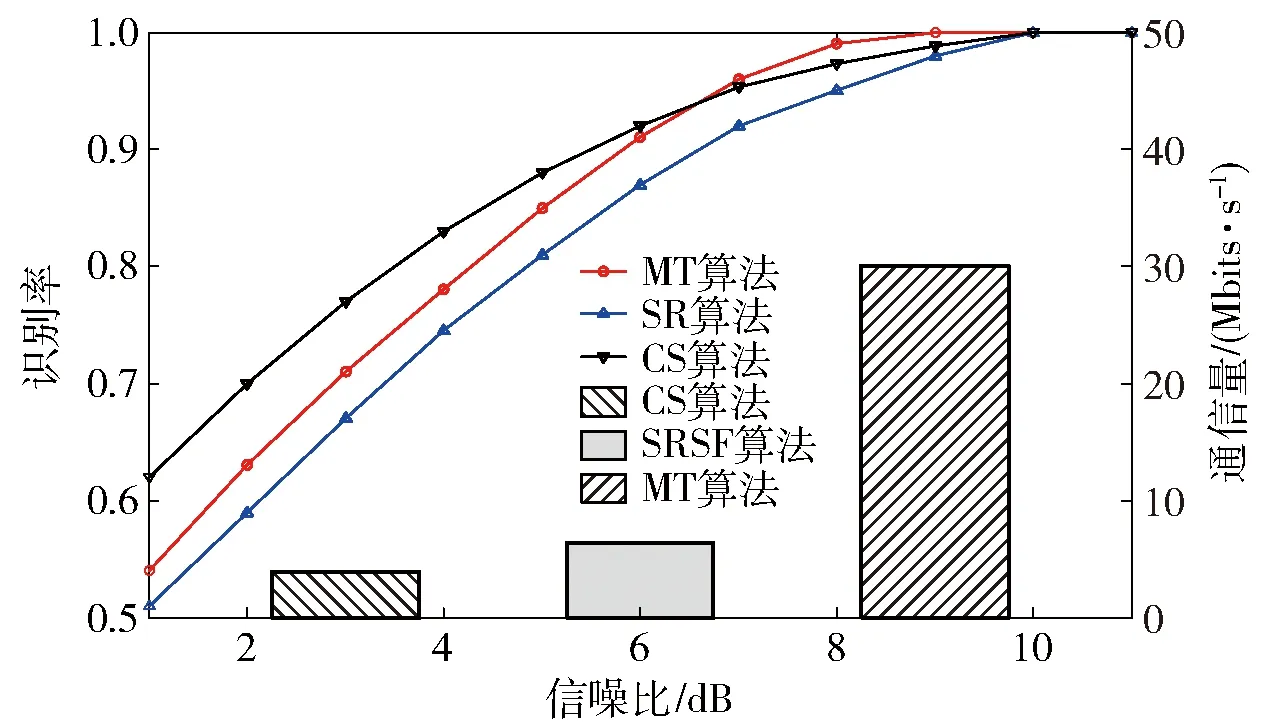
图8 不同信噪比下算法的识别率和各算法的通信量Fig.8 Correct identification rates of algorithms at different SNRs and traffics of algorithms

实验结果表明：当信噪比≥6 dB时，基于CS的相关融合识别算法能实现90%以上的识别率，验证了识别算法的可行性；当信噪比较小时，相关融合算法的识别率要优于其他两种算法；随着信噪比的增加，不同算法的识别率均逐渐提高，但相关融合算法的优势减小，当信噪比≥7 dB时，MT算法识别性能优于相关融合算法。通信量方面，MT算法的通信量远大于SRSF算法和本文提出算法，基于CS的相关融合识别算法通信量最小。基于CS的相关融合识别算法具有良好的识别性能，在低信噪比时识别性能突出，并且在保证识别率的同时降低了对通信量的要求。

3.3 不同融合规则的融合性能

为了对比不同融合规则在多源测量向量融合中的融合效果，用融合后测量值与完整信号测量值的数据相似度DS作为衡量不同融合规则性能的标准，将常见的活跃度最大融合规则、熵权融合规则和相关性融合规则进行对比。利用(13)式计算数据相似度DS：

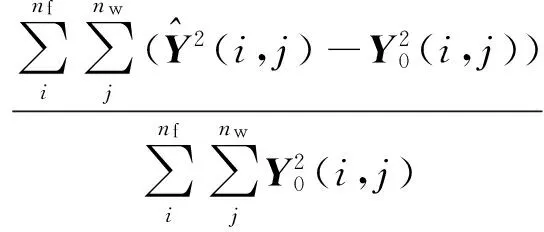
(13)

活跃度最大融合规则将时频矩阵的测量值作为活跃度，融合时取多源测量值的最大值作为融合结果[2]，即

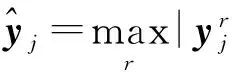
(14)

熵权融合规则对测量值进行线性融合

(15)

式中：权重调节项ωr由测量值的联合信息熵和互信息熵确定[16]。

仿真参数设置与3.1节相同，计算不同融合规则下融合后测量值与完整信号测量值的数据相似度，为凸显融合效果，计算缺失信号测量值与完整信号测量值的数据相似度与融合信号进行对比。进行1 000次独立重复实验，并对结果作统计分析，仿真结果如表1所示。由实验结果可知：与缺失信号相比，融合后的信号均具有较高的数据相似度，并且相关性融合规则优于熵权融合规则，熵权融合规则优于活跃度最大规则。相关性融合规则将相关系数引入权重调节项，保留了更为全面的辐射源信息，同时有效抑制了噪声。

表1 不同融合规则下数据相似度的统计数据

在相关性融合规则中，相关度阈值ξ的取值对融合结果影响很大，为优化ξ取值，对ξ进行灵敏度分析。ξ取[0.2, 0.5]，其他仿真条件不变，计算融合后测量值与完整信号测量值的数据相似度，采用Kernel加权平滑方法处理数据，保留最优相关阈值。如图9所示，仿真结果表明，随着ξ增大，噪声信号被抑制，数据相似度增大，到达最优相关阈值ξ0=0.2975后，由于ξ到达一定值后，有用信号也被抑制，相似度随相关度阈值ξ增大而急剧减小。

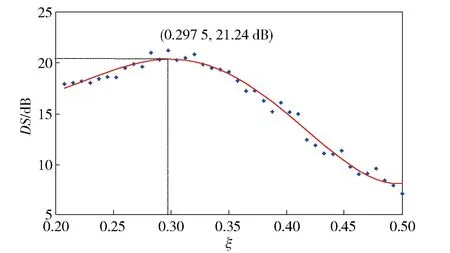
图9 相关度阈值ξ灵敏度分析Fig.9 Sensitivity analysis of correlation threshold ξ

4 结论

针对协同侦察数据层融合识别中通信量大的问题，引入CS技术，建立基于CS的雷达信号数据级融合识别模型，提出了基于CS的相关融合识别算法。算法在数据级融合多源信息，提高了信息利用率，能处理脉冲缺失、畸变等复杂情况；采用CS技术，将高维雷达信号随机压缩投影到低维空间，保证识别性能的同时大幅降低了通信代价；提出基于测量向量相关性的融合规则，相比于目前在CS融合中常用的活跃度最高和平均熵等融合规则，具有更好的融合性能，在应对低信噪比时效果明显。

References)

[1] 王星，程嗣怡，周东青，等. 航空电子对抗组网[M]. 北京：国防工业出版社，2016. WANG Xing，CHENG Si-yi，ZHOU Dong-qing，et al. Avionics countermeasure networking [M]. Beijing: National Defense Industry Press, 2016. (in Chinese)

[2] 马捷，黄高明，吉嘉，等. 基于稀疏表示的雷达辐射源信号级融合识别算法[J]. 控制与决策. 2014，29(10)：1798-1802. MA Jie，HUANG Gao-ming，JI Jia，et al. Signal-level fusion algorithm for radar emitter identification based on sparse representation[J]. Control and Decision，2014，29(10)：1798-1802. (in Chinese)

[3] 王杰贵，靳学明，罗景青. 基于ESM和ELINT信息融合的机载辐射源识别[J]. 电子学报. 2006，34(3)：424-428. WANG Jie-gui，JIN Xue-ming，LUO Jing-qing. Airborne emitter recognition based on multi-sensor data fusion of ESM and ELINT[J]. Acta Electronica Sinica, 2006，34(3)：424-428. (in Chinese)

[4] 韩崇昭，朱洪艳，段战胜，等. 多源信息融合[M]. 第2版. 北京：清华大学出版社，2010. HAN Chong-zhao，ZHU Hong-yan，DUAN Zhan-sheng, et al. Multi-source information fusion [M]. 2nd ed. Beijing: Tsinghua University Press, 2010. (in Chinese)

[5] 王永成，王宏飞，杨成梧. 目标属性信息相关时融合识别的实现方法[J]. 兵工学报, 2005，26(3)：338-342. WANG Yong-cheng，WANG Hong-fei，YANG Cheng-wu. Method of implementation of fusing correlated attribute information in target recognition [J]. Acta Armamentarii, 2005，26(3)：338-342. (in Chinese)

[6] 尚朝轩，王品，韩壮志. 基于类决策树分类的特征层融合识别算法[J]. 控制与决策, 2016，31(6)：1009-1014. SHANG Chao-xuan，WANG Pin，HAN Zhuang-zhi. Feature-level fusion recognition algorithm based on analogy decision tree classification[J]. Control and Decision, 2016，31(6)：1009-1014. (in Chinese)

[7] 彭颖，沈怀荣，马永一. 一种新的冲突证据融合方法[J]. 兵工学报, 2011，32(1)：78-84. PENG Ying，SHEN Huai-rong，MA Yong-yi. A new fusion method for conflicting evidence[J]. Acta Armamentarii, 2011，32(1)：78-84. (in Chinese)

[8] 张燕君，龙呈. 基于证据理论的目标识别方法[J]. 系统工程与电子技术, 2013，35(12)：2467-2470. ZHANG Yan-jun，LONG Cheng. Target recognition method based on evidence theory[J]. System Engineering and Electronics, 2013，35(12)：2467-2470. (in Chinese)

[9] 黄高明，吉嘉. 基于多分辨率分析的雷达辐射源融合识别算法[J]. 海军工程大学学报, 2014，26(3)：61-65. HUANG Gao-ming，JI Jia. Radar emitter identification based on multiresolution analysis[J]. Journal of Naval University of Engineering,2014，26(3)：61-65. (in Chinese)

[10] Kutyniok G. Compressed sensing: theory and applications[J]. Corr, 2012, 52(4):1289-1306.

[11] Michael E. Sparse andredundant representations[M]. New York: Springer，2010.

[12] 邵文泽，韦志辉. 压缩感知基本理论[J]. 中国图像图形学报, 2012，17(1)：1-12. SHAO Wen-ze，WEI Zhi-hui. Advances and perspectives on compressed sensing theory[J]. Journal of Image and Graphics, 2012，17(1)：1-12. (in Chinese)

[13] Candes E，Romberg J，Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006，52(2)：489-509.

[14] 高威. 基于小波及原子库的信号脉内调制方式分析算法研究[D]. 哈尔滨：哈尔滨工业大学，2015. GAO Wei. Research on signal intra-pulse modulation analysis algorithms based on wavelet and time-frequent atom dictionary[D]. Harbin：Harbin Institute of Technology, 2015. (in Chinese)

[15] Skolnik M I. 雷达手册 [M]. 第3版. 周万幸，译.北京：电子工业出版社，2010. Skolnik M I. Radar handbook [M]. 3rd ed. ZHOU Wan-xing, translated. Beijing：Publishing House of Electronics Industry，2010. (in Chinese)

[16] Luo X Y，Zhang J，Yang J Y，et al. Image fusion in compressed sensing[C]∥2010 International Conference on Image Processing. Cairo，Egypt：IEEE，2010：2205-2208.

Data-level Fusion for Emitter Signal Identification Based on Compressed Sensing

WANG Zhi-peng， WANG Xing， TIAN Yuan-rong， ZHOU Yi-peng

(Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, Shaanxi, China)

A novel data-level fusion method for emitter identification is proposed for the large scale communication in cooperative reconnaissance, which uses the superiority of compressed sensing in representing an original signal by using few measured data. In the proposed method, the Gabor time-frequency data of intercepted signal in a receiver is compressively measured with a Gaussian random measurement matrix. By transmitting few compressively measured data rather than the original signal, the large scale communication problem is alleviated. In the fusion center, a correlation fusion rule is proposed to calculate the combined weight of measured data according to the correlation among compressively measured data. To identify the signal type, a dictionary library is trained with every possible signal, and the reconstruction error in the sub-dictionary is calculated. The signal type with minimum reconstruction error is just the identification result. The simulated result proves that the proposed method achieves a pretty good balance in identification rate and communication scale, especially under low signal-to-noise ratio. Compared to the existed algorithms, the correlation fusion rule keeps more details of original signal.

ordnance science and technology; emitter identification; data-level fusion; compressed sensing; time-frequency transform; correlation fusion rule

收信号x1、x2、x3的时域图和Gabor变换时频图 Fig.6

signals x1，x2，x3 in time domain and time-frequency domain

2017-01-06

航空科学基金项目(20152096019)

王志鹏(1993—)，男，硕士研究生。E-mail：wzp_1993@yeah.net

王星(1965—)，男，教授，博士生导师。E-mail：m18165380023_1@163.com

TN911.72

A

1000-1093(2017)08-1547-08

10.3969/j.issn.1000-1093.2017.08.012