三轴旋转惯性导航系统的旋转控制建模研究

查峰， 覃方君， 李京书， 叶斌

(1.海军工程大学 电气工程学院, 湖北 武汉 430033; 2.惯性技术航空科技重点实验室, 陕西 西安 710061)

三轴旋转惯性导航系统的旋转控制建模研究

查峰1， 覃方君1， 李京书1， 叶斌2

(1.海军工程大学 电气工程学院, 湖北 武汉 430033; 2.惯性技术航空科技重点实验室, 陕西 西安 710061)

为了减小载体运动对于旋转惯性导航系统误差调制作用的影响，建立三轴旋转惯性导航系统在隔离载体运动条件下的控制模型。基于三轴框架结构定义合理的坐标系，分析载体运动在三轴框架中的传递过程，建立载体运动与周期性旋转惯性测量单元运动之间的数学解析关系。在此基础上，根据欧拉动力学方程，建立三轴框架运动与电机力矩、载体运动之间的动力学模型。联合载体运动传递过程和动力学模型，建立三轴旋转惯性导航系统在隔离载体运动条件下的控制模型，得到了载体运动过程中外环轴上的转动惯量随俯仰角而实时变化的解析形式。仿真和实际实验验证了理论分析结果，可为旋转控制算法设计提供理论参考。

控制科学与技术； 惯性导航； 旋转控制； 动力学模型； 旋转惯性导航系统

0 引言

旋转惯性导航系统是通过周期性旋转惯性测量单元(IMU)，改变惯性器件的指向以调制其常值误差和慢变误差，从而提高系统精度[1]。按照IMU旋转轴数目不同，可将系统分为单轴、双轴以及三轴旋转惯性导航系统。采用不同旋转策略的惯性导航系统，其误差特性和传递规律也不相同[2-3]。

目前针对旋转惯性导航系统的研究，大多数从旋转策略出发，分析各个误差源在不同旋转策略下的误差传播特性[1-6]。文献[4]集中分析了单轴、双轴旋转惯性导航系统对于器件误差和系统误差的调制效果，并指出由于双轴系统不能提供空间的3个自由度，因此载体运动会与器件误差耦合从而引起惯性导航系统误差。文献[5-6]提出了三轴旋转惯性导航系统方案，并指出如果能够使IMU不受载体角运动影响，相对于惯性空间做周期性旋转，可以进一步抑制载体角运动、地球自转与刻度系数误差的耦合。因此，隔离载体角运动的旋转策略研究受到广泛重视[7-8]。

若隔离载体角运动，需要构建三轴框架的旋转惯性导航系统，使得IMU相对于惯性空间有规律转动。载体存在角运动(横摇、纵摇和航向运动)时，三轴框架因隔离载体角运动使得框架轴系间角度关系实时变化，不同轴系间存在运动耦合。因此，针对隔离载体运动条件下的三轴框架进行旋转控制变得较为复杂。目前，针对三轴稳定平台控制建模一般将每个轴向回路作为单独控制系统进行分析[9-10]，没有建立统一的三轴控制系统的数学模型。针对不同轴向间的运动耦合仅以干扰力矩等效，未进行定性分析。文献[11-12]对三轴转台的运动耦合与解耦问题进行了研究,但分析还是基于单轴控制回路模型，仅仅将耦合运动看成是干扰力矩，通过自适应算法抑制干扰力矩影响。文献[13]关注了多轴旋转中的耦合关系，并对非线性解耦进行了分析，可为三轴转台的解耦提供一种参考。但耦合分析时基于给定的三轴转台的已知模型，未对一般三轴框架系统的旋转控制进行分析建模，且三轴转台应用场合一般为某一轴转动时其他两轴静止。三轴旋转惯性导航在隔离载体角运动时，3个轴向同时转动，轴系间的运动传递、动力方程更加复杂。

本文针对隔离载体运动条件下三轴旋转惯性导航系统，通过构建合理的坐标系，从理论上推导因载体角运动引起的框架运动在不同轴间的传递形式，得到陀螺输出、框架运动和电机驱动力矩之间的数学关系，建立三轴旋转惯性导航系统的旋转控制模型，为控制算法设计提供理论参考。

1 三轴框架结构与坐标系定义

按结构组成不同，可将惯性导航系统分为平台式和捷联式两种。捷联式惯性导航直接将IMU固定联接在载体上，直接量测载体的运动信息。平台式惯性导航为IMU提供一个稳定平台，平台能够有效隔离载体的角运动而跟踪某一坐标系，在该坐标系内对加速度信息进行提取从而得到速度和位置。20世纪80年代以来，随着惯性技术及系统误差补偿技术的发展，逐渐形成了旋转惯性导航系统的结构形式。

1.1 三轴框架结构

旋转惯性导航系统是一种不同于捷联式惯性导航系统和平台式的中间形式，其结构可理解为在捷联式基础上按照旋转轴的数目增加了由电机驱动的旋转机构，使原来固定联接的IMU可以绕一定规律旋转。而对于三轴旋转惯性导航系统，其框架结构与普通的平台式惯性导航类似，其示意图如图1所示。

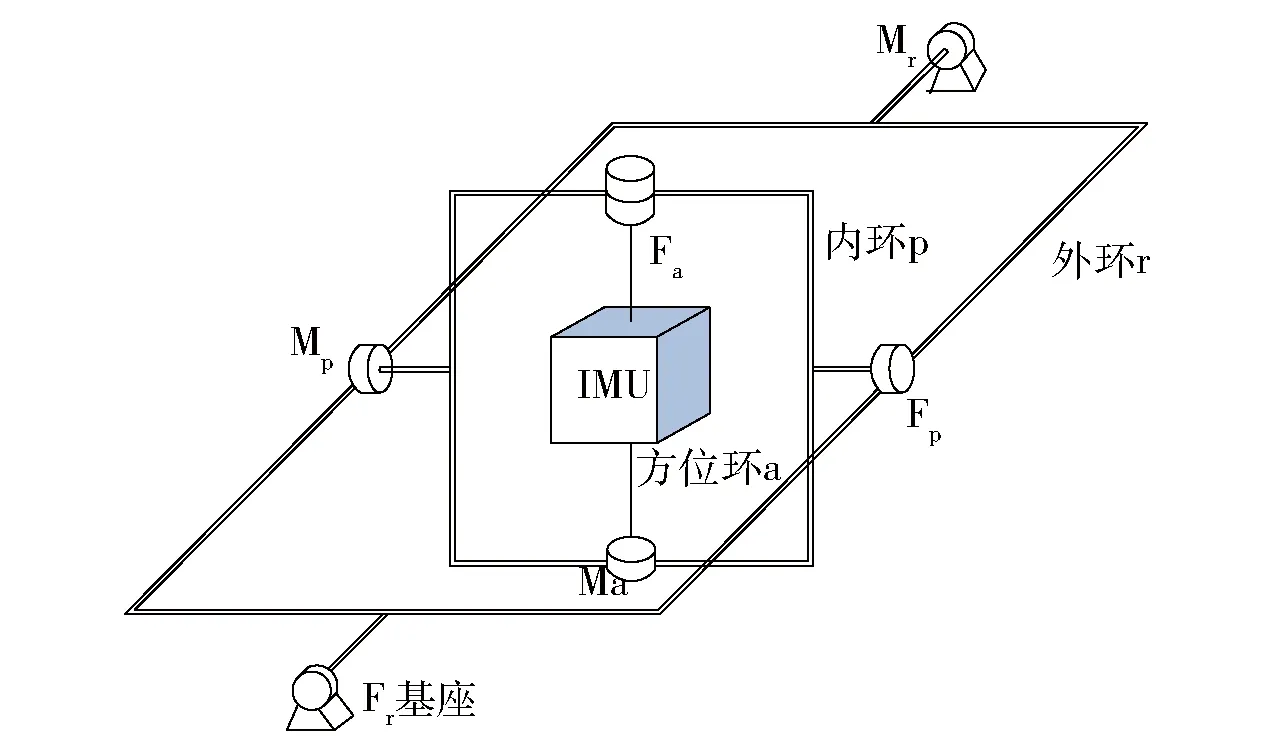
图1 三轴框架结构示意图Fig.1 Structure of triaxial frame

图1中IMU利用三轴框架联接，由外向内分别为外环r、内环p、方位环a，在每个环架转动轴的两个端面分别装有力矩电机Mr、Mp、Ma和角度传感器Fr、Fp、Fa. 方位环与IMU直接固定联接，其转轴称为方位轴，方位轴通过框架联接在内环上，内环通过内环轴联接在外环上，外环通过外环轴与基座联接。从上述结构可以看出，在力矩电机Mr、Mp、Ma的驱动下，外环可以绕外环轴相对于基座转动，内环可以绕内环轴相对于外环转动，IMU可以绕方位轴相对于内环转动。

1.2 坐标系定义

为了便于分析IMU在三轴框架下的运动，首先对本文坐标系做如下定义：

1)基座(载体)坐标系OXbYbZb，简称b系，与载体基座固定联接，其Xb轴、Yb轴、Zb轴三轴分别指向载体的右方向、前方向、上方向。

2) IMU坐标系OXpYpZp，简称p系，该坐标系与IMU固定联接，Zp轴沿方位轴向上，Xp轴、Yp轴在与Zp轴垂直的一个平面上，构成右手直角坐标系。

3)内环坐标系OXfYfZf，简称f系，与内环固定联接，Zf轴为IMU方位轴(同Zp轴)，Xf轴沿内环轴指向右侧，Yf轴与Xf轴、Zf轴垂直构成右手直角坐标系。

4)外环坐标系OXrYrZr，简称r系，与外环固定联接，Xr轴沿平台内环轴指向右(同Xf轴)，Yr轴沿平台外环轴指向前，Zr轴与Xr轴、Yr轴垂直构成右手直角坐标系。由于外环平面与内环平面不一定垂直，Zr轴与方位轴指向并不始终一致。

5)电机坐标系OXmYmZm，简称m系，因为沿方位轴Zp轴、内环轴Xf轴、外环轴Yr轴各装有一个力矩电机，故OXfYrZp组成了力矩电机坐标系，记为OXmYmZm. 需要注意的是，载体存在角运动时，方位轴、内环轴和外环轴不一定正交，因此电机坐标系不一定是正交坐标系。

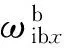
下面根据上述坐标系和符号定义，分析载体角运动条件下IMU的绝对角运动。

2 IMU的绝对角运动分析

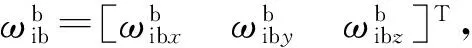
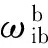
(1)

而基座转动的X轴和Z轴与外环属于刚性约束，因此基座转动的X轴和Z轴分量刚性传递到外环。由于外环相对于载体系转过角度Q，因此基座转动传递到外环坐标的分量为

(2)

将上述关系写成矩阵形式有

(3)

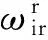
(4)

同理，外环转动的Y轴和Z轴与内环属于刚性约束，因此外环转动的Y轴和Z轴分量刚性传递到内环。由于内环相对于外环系X轴转过角度P，因此外环转动传递到内环坐标的分量为

(5)

将上述关系写成矩阵形式有

(6)

由此得到了内环相对于惯性系转动的绝对角速度。同时，内环转动会传递到方位轴上，即IMU上。由于方位轴与内环坐标系Z轴重合，因此内环坐标系转动的Z轴分量将被隔离，此时方位环转过了角度A. 类似以上分析，内环转动传递到IMU上可以写成如下形式：

(7)

IMU的方位轴为Z轴，因此得到其绝对角速度为

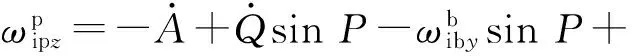
(8)

依次将(3)式、(6)式代入(8)式，得到载体转动传递到IMU上的形式为

(9)

(9)式表示了IMU相对于惯性系的绝对角速度。从(9)式可以看出，第1个系数矩阵表示电机坐标系转动到IMU坐标系的传递矩阵，而第2个系数矩阵表示载体运动通过刚性约束传递到IMU坐标系的传递矩阵。

为了后续分析，可记作：

(10)

3 三轴力矩方程

根据欧拉动力学方程，IMU的转动是绕坐标原点的定点转运，其电机力矩方程[14]可以表示为

(11)

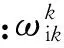
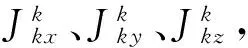
(12)

对(12)式求导后代入(11)式得

(13)

在确定台体(方位环)的绝对角速度后，根据(13)式可得作用在台体上的力矩。需要注意的是，对于台体只有与其紧邻的内框架对其具有反作用力矩，同时内框架只有外框架对其有反作用力矩。由内向外，可以依次求得各框架上的作用力矩。

3.1IMU的力矩方程

设IMU绕IMU坐标系3个轴向的转动惯量为Jpx、Jpy、Jpz，由于IMU为最内层框架，因此不存在反作用力矩。根据欧拉动力学方程，可得

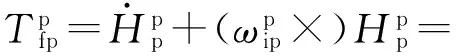
(14)

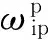
(15)

3.2IMU与内环组合体

IMU绕方位轴转动，同时IMU与内环框架一起绕内环轴转动。设IMU与内环组合体在内环坐标系3个轴向上的转动惯量为Jfx、Jfy、Jfz，根据欧拉动力学方程可得内环框架上的动力学方程为

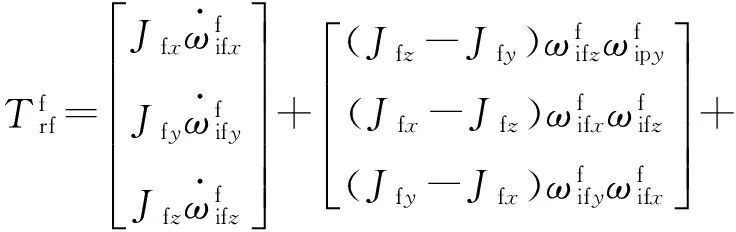
(16)

由于IMU与内环组合体绕内环坐标系X轴转动，设其摩擦力矩为Df，因此忽略角速度乘积项，可得内环轴上的力矩方程为

(17)

将(9)式代入(17)式，忽略角速度乘积项得

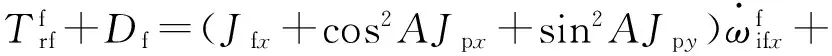
(18)

3.3 外环、内环与IMU组合体

外环、内环与IMU的组合体绕外环轴转动。设该组合体在外环坐标系3个轴向上的转动惯量为Jrx、Jry、Jrz，根据欧拉动力学方程可得内环框架上的动力学方程为

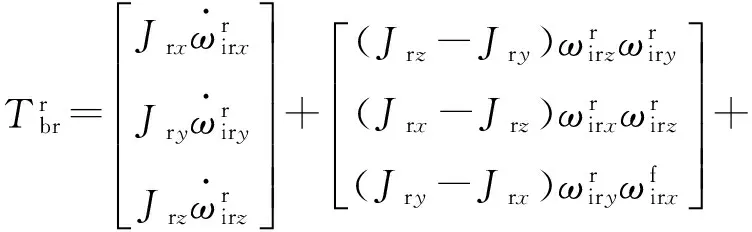
(19)

由于外环、内环与IMU的组合体绕外环坐标系Y轴转动，设其摩擦力矩为Dr，因此忽略角速度乘积项，可得外环轴上的力矩方程为

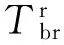
(20)

联合(15)式、(18)式、(20)式可得三轴旋转惯性导航系统的三轴框架的力矩方程。显然，方位轴上的力矩方程相对独立，只与该轴向上的角速度和角加速度有关。内环轴与外环轴会因为方位角A和俯仰角P而产生耦合。

假设台体在IMU的水平方向上对称，记Jpx=Jpy=Jpz=Jp0，则三轴框架的力矩方程可简化为

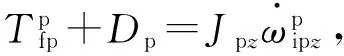
(21)

上述力矩方程组表示了在三轴框架的力矩与每个轴向上的转动角速度关系。而在三轴旋转惯性导航系统的控制过程中，力矩电机利用陀螺仪输出数据进行控制，使得IMU能够隔离载体运动，同时在固定坐标系内按规律旋转。从第3个力矩方程可知，当载体存在角运动时，其外环轴上的转动惯量随转动角度P变化，这对系统控制算法提出了更高要求。

4 系统控制建模与分析

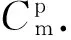
(22)

综上所述，(1)式、(4)式、(8)式表示三轴旋转惯性导航系统的三轴框架在力矩电机作用下产生的角运动。该角运动通过(22)式传递到IMU上，从而被陀螺仪敏感而输出角运动信息。三轴旋转惯性导航系统的控制模块根据陀螺仪输出的电压信息Ug，经过相应的电压电流转换为电流信号，转换系数为ka，因此有控制电流ia的关系式：

ia=kaUg.

(23)

采用合适的控制算法(一般为PID控制)控制框架电机的驱动力矩。三轴旋转惯性导航系统一般采用直流力矩电机，三轴框架系统在驱动力矩作用下转动，电机输出力矩与电枢电流ia呈比例关系：

Tm=kmia.

(24)

综合(23)式、(24)式得到了陀螺控制信息与电机输出力矩的关系为

Tm=kmkaUg=KmUg.

(25)

在电机力矩Tm作用下框架轴开始转动，转动被传递到IMU上，从而形成闭环反馈形式，由此构建了三轴旋转惯性导航系统的控制模型。

根据上述控制流程，由(21)式、(22)式、(25)式可得三轴旋转惯性导航系统的控制框图如图2所示。

图2 三轴旋转惯性导航的控制框图Fig.2 Control block diagram of triaxial rotating INS

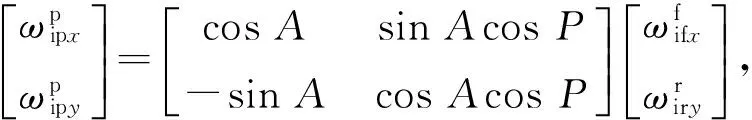
(26)

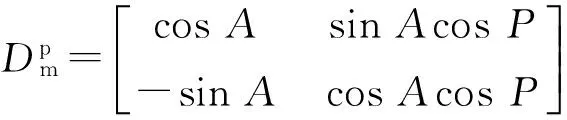
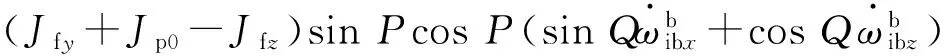
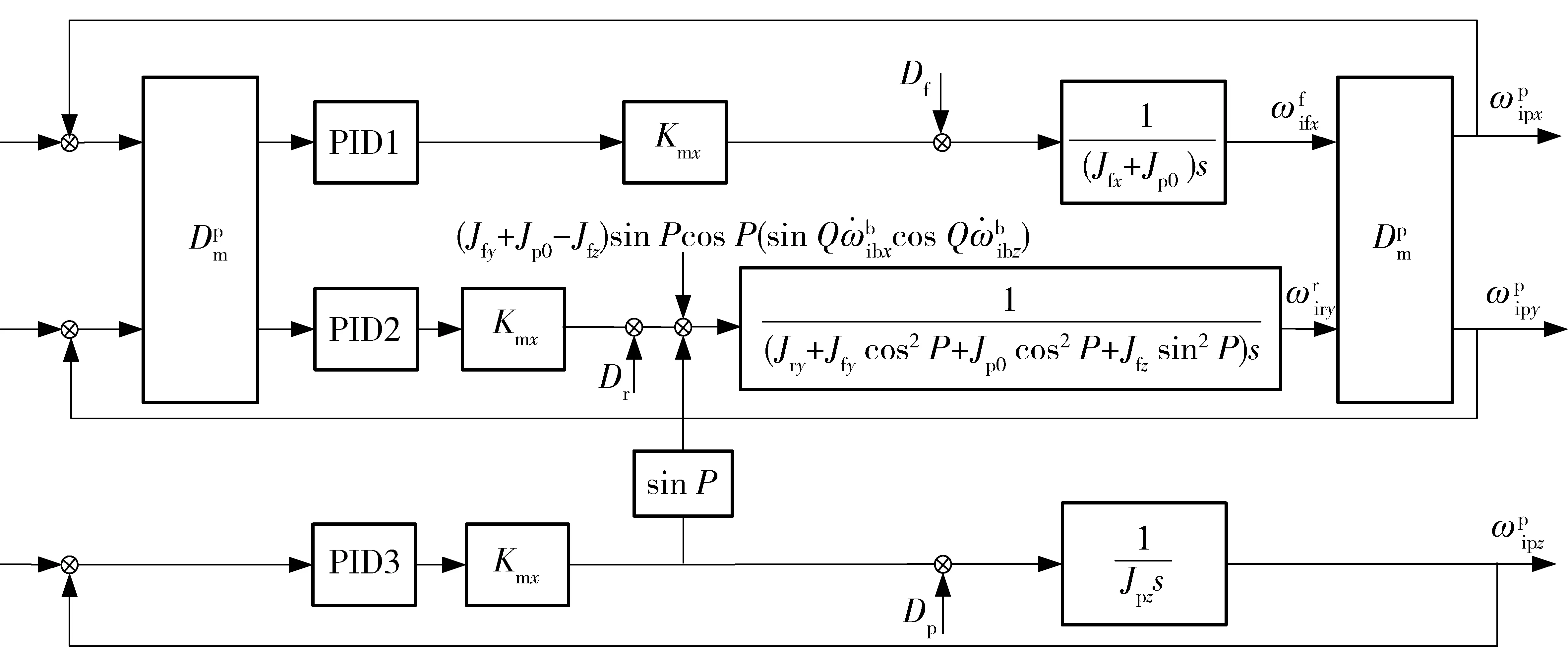
图3 三轴旋转惯性导航的解耦控制框图Fig.3 Block diagram of decoupling control of triaxial rotating INS

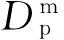
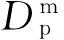
5 仿真与试验

首先进行三轴旋转惯性导航系统的旋转控制仿真，三轴系统的仿真物理参数参照实验室实际双轴稳定平台设定。设IMU、内环、外环及其组合体在空间内具有对称结构，IMU 3个轴向的转动惯量Jpx=Jpy=Jpz=1.5 kg·m2，IMU与内环框架在3个轴向的转动惯量Jfx=Jfy=Jfz=1.8 kg·m2,同时，IMU与内环、外环的组合体在3个轴向的转动惯量Jrx=Jry=Jrz=2.2 kg·m2. 3个轴向电机的力矩系数Kmx=Kmy=Kmz=3.95 N·m/V.

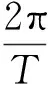
根据舰船在海上的运动情况，设横摇、纵摇、航向的幅值θ0=12°、γ0=5°、φ0=4°，周期分别为10 s、8 s和12 s，初始相位分别为φ1=10°、φ2=20°、φ3=30°.

为了隔离其他误差源对控制效果的影响，仿真中不考虑器件误差、外界扰动等其他误差，利用单回路整定理想的PID参数进行三轴惯性导航旋转控制仿真。

首先根据控制系统各参数，分别对方位环、内环和外环进行单回路控制系统仿真。为有效观测载体运动周期内控制误差的变化，仿真时间设为24 s. 利用临界比例度法整定每个通道的PID参数，然后利用整定的PID参数，进行上述角运动下方位环、内环和外环的单回路控制仿真，其控制误差如图4所示。由图4可知，整定的PID参数对单个回路取得了满意的控制效果。

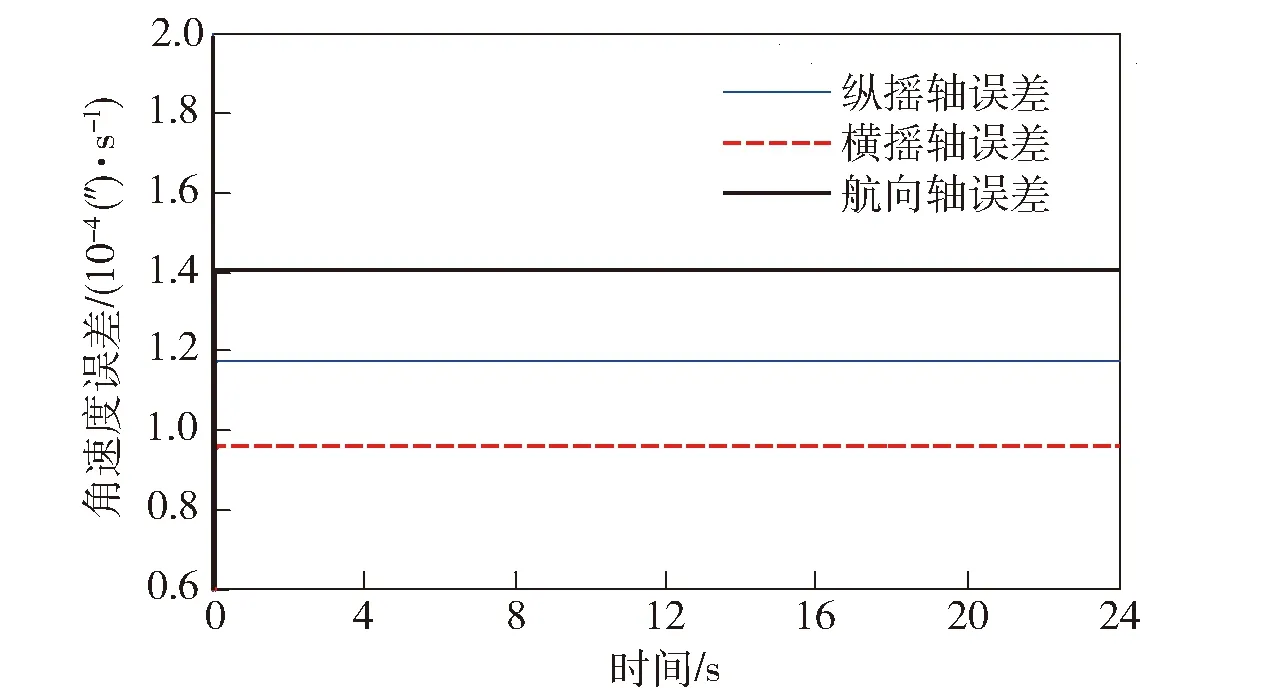
图4 单通道旋转控制误差Fig.4 Rotation control error of single axis

在此基础上，利用单回路整定的PID参数，进行三轴旋转惯性导航系统的控制。控制误差如图5所示。从图5可以看出，航向轴(方位轴)误差与单通道回路相同，不受耦合影响。而纵摇轴和横摇轴误差与单回路控制相比显著增加，且呈现出周期性的波动。通过改变载体运动周期和误差频率分析可知其周期性与载体运动相关，由此验证了本文理论分析结果。

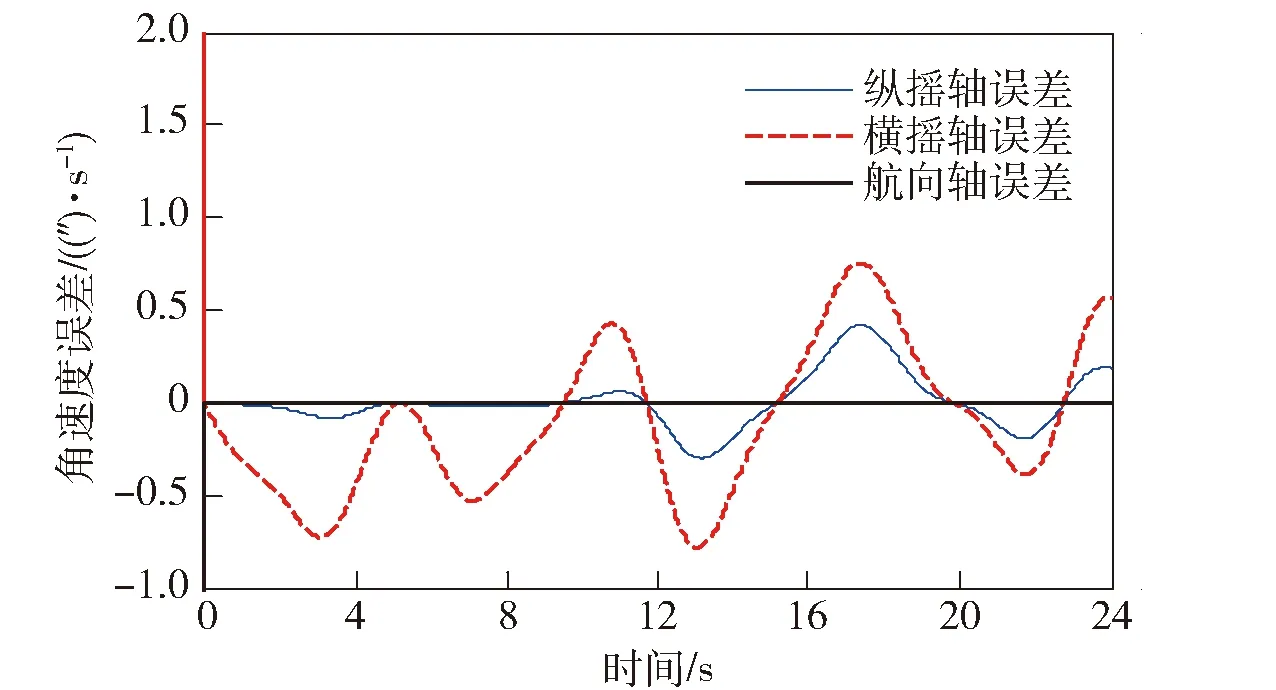
图5 三轴旋转控制误差Fig.5 Rotation control errors of three axes

为了进一步验证本文控制系统建模的准确性，进行了双轴稳定平台(两个水平轴可以旋转，方位轴固定)的控制系统试验。如图6所示，将双轴稳定平台安置在摇摆台上，由摇摆台模拟载体运动，运动周期10 s. 首先利用整定的PID参数分别进行单通道的控制试验，控制误差如图7所示(需要指出：图7中数据的阶跃变化是由于角速度传感器的分辨率所致)，可见系统控制平稳。在利用整定的PID参数进行双轴控制系统试验，由于两个回路的耦合产生了与摇摆同周期的控制误差(见图8)，进一步验证了本文的理论分析结果。

图6 双轴稳定平台在摇摆台上的控制试验Fig.6 Control test of two-axis stable platform on rocking table

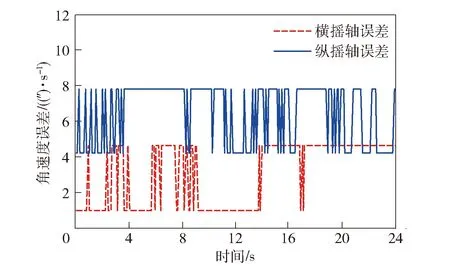
图7 单通道控制误差Fig.7 Rotation control error of single axis

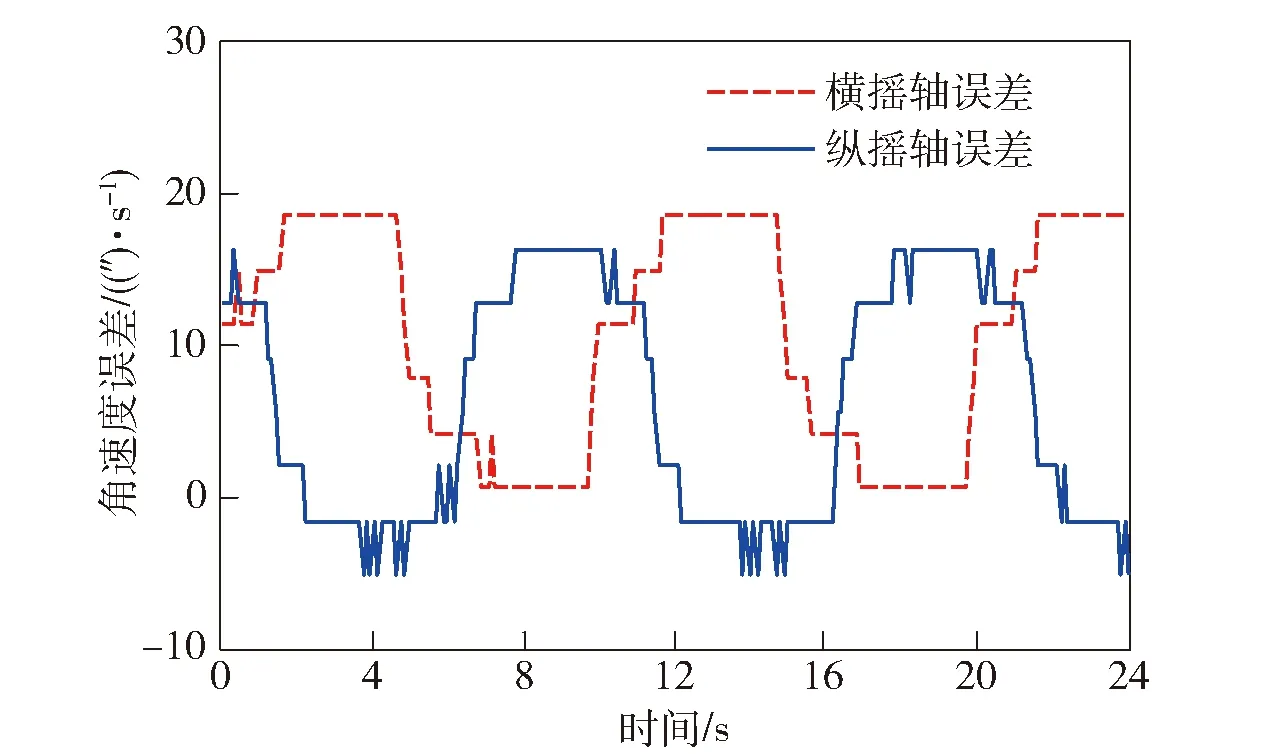
图8 双轴控制误差Fig.8 Rotation control errors of two axes

6 结论

为了最大程度上减小载体运动和地球转动对旋转惯性导航误差的抑制效果，使IMU绕惯性系而非载体系旋转的方案受到广泛重视。在多轴旋转条件下，隔离载体角运动使得各轴之间的运动相互耦合和影响，系统运动和控制模型更加复杂。本文在建立三轴框架坐标系的基础上，分析载体运动到IMU的传递过程与形式，建立了各框架运动的数学解析关系。根据欧拉动力学方程，推导了在隔离载体运动条件下陀螺输出、驱动力矩和三轴框架转动角速度之间的动力学方程。在此基础上，建立了三轴旋转惯性导航系统的三轴控制模型与方框图。通过控制模型可知：除IMU坐标系的方位轴可以独立控制外，内外环的框架运动相互耦合，且外环轴上的转动惯量随载体俯仰角变化而实时变化。仿真与实际试验验证了本文的理论分析结果。后续研究应根据建立的三轴旋转惯性导航系统的三轴控制模型，设计科学、合理的旋转控制算法以提高载体角运动条件下的控制精度。

References)

[1] 袁保伦．四频激光陀螺旋转式惯导系统研究[D]．长沙:国防科学技术大学，2007． YUAN Bao-lun. Research on rotating inertial navigation system with four-frequency differential laser gyroscope[D]. Changsha: National University of Defense Technology, 2007. (in Chinese)

[2] Yuan B L，Miao D，Han H L. Error compensation of an optical gyro INS by multi-axis rotation[J]. Measurement Science and Technology,2012, 23(2):25102-25110.

[3] 杨国梁，王玮．基于双轴旋转的惯导系统误差自补偿技术[J]．北京航空航天大学学报，2012，38(4):519-524. YANG Guo-liang, WANG Wei. Error auto-compensation technology of inertial navigation system based on double-axis rotation[J]．Journal of Beijing University of Aeronautics and Astronautics，2012，38(4):519-524. (in Chinese)

[4] Zha F，Xu J N，Qin F J．Error analysis for SINS with different IMU rotation scheme[C]∥International Asia Conference on Informatics in Control, Automation and Robotics．Wuhan:IEEE,2010：422-426．

[5] 孙枫，王秋滢.三轴旋转捷联惯导系统旋转方案设计[J].仪器仪表学报,2013,34(1)：65-72. SUN Feng, WANG Qiu-ying. Rotation scheme design for modulated SINS with three rotating axes[J].Chinese Journal of Scientific Instrument,2013,34(1)：65-72. (in Chinese)

[6] Zhang l，Liu J Y，Lai J Z. Rotating fiber optic gyro strapdown inertial navigation system with three rotating axes[J].Transactions of Nanjing University of Aeronautics and Astronautics, 2008, 25(4):289-293.

[7] 许江宁，查峰，李京书，等．单轴旋转惯导系统的"航向耦合效应"抑制算法[J]．中国惯性技术学报, 2013,21(1):26-30. XU Jiang-ning, ZHA Feng, LI Jing-shu, et al. Analysis and compensation for heading-coupling effect of single-axis rotating INS[J]．Journal of Chinese Inertial Technology，2013,21(1):26-30. (in Chinese)

[8] 张伦东，练军想，吴美平，等．单轴旋转惯导系统载体航向隔离方法研究[J]．仪器仪表学报，2012，33( 6):1247-1253． ZHANG Lun-dong, LIAN Jun-xiang, WU mei-ping, et al. Research on yaw angle isolation method of inertial navigation system based on single-axis rotation[J]．Chinese Journal of Scientific Instrument,2012,33(6):1247-1253．(in Chinese)

[9] 周向阳,赵强.航空遥感三轴惯性稳定平台双速度环控制[J].中国惯性技术学报,2014,21(4):439-445. ZHOU Xiang-yang, ZHAO Qiang. Dual rate-loop control method of three-axis inertially stabilized platform for aerial remote sensing application[J]. Journal of Chinese Inertial Technology,2014,21(4):439-445.(in Chinese)

[10] 杨蒲,李奇.三轴陀螺稳定平台控制系统设计与实现[J].中国惯性技术学报,2007,15(2):171-176. YANG Pu,LI Qi. Design and realization of control system for three-axis gyro stabilized platform[J]. Journal of Chinese Inertial Technology,2007,15(2):171-176.(in Chinese)

[11] 李付军,雒宝莹,曾军高,等.3轴电动转台动力耦合分析及抑制策略[J].上海交通大学学报,2011,45(2):202-206. LI Fu-jun,LUO Bao-ying,ZENG Jun-gao, et al. Analysis and control strategy of a three-axis electric rotary table dynamic coupling[J]. Journal of Shanghai Jiao Tong University,2011,45(2):202-206.(in Chinese)

[12] 林存海,曹广锋.基于改进型重复控制的三轴转台解耦与控制[J].光电技术应用,2014,29(2):79-86. LIN Cun-hai, Cao Guang-feng. Decoupling and control of three-axis turret based on modified repetitive control system [J]. Electro-optic Technology Application, 2014, 29 (2):79-86.(in Chinese)

[13] 王茂,邵长东.带有轴间动力学解耦的三轴转台自适应控制[J].中国惯性技术学报,2003,11 (5) :5-11. WANG Mao, SHAO Chang-dong. Adaptive control for three-axle table based on dynamics decoupling between frames[J]. Journal of Chinese Inertial Technology, 2003,11 (5):5-11.(in Chinese)

[14] 高钟毓.惯性导航系统技术[M]. 北京：清华大学出版社，2012. GAO Zhong-yu. Inertial navigation system technology[M]. Beijing：Tsinghua University Press,2012. (in Chinese)

[15] 刘维平，袁磊，刘西侠. 三轴全轮转向车辆水平集成控制研究[J].兵工学报，2016,37(2):203-209. LIU Wei-ping,Yuan Lei, LIU Xi-xia. Study of integrated control of all-wheel-steering three-axil vehicle[J]. Acta Armamentarii，2016,37(2):203-209.(in Chinese)

[16] 王昭磊,王青,冉茂鹏，等.基于自适应模糊滑模的复合控制导弹制导控制一体化反演设计[J].兵工学报，2015,36 (1) :78-85. WANG Zhao-lei, WANG Qing, RAN Mao-peng, et al. Integrated guidance and control backstepping design of blended control missile based on adaptive fuzzy sliding mode control [J]. Acta Armamentarii，2015,36(1):78-85.(in Chinese)

Rotation Control Modeling of Triaxial Rotating Inertial Navigation System

ZHA Feng1， QIN Fang-jun1， LI Jing-shu1， YE Bin2

(1.College of Electrical Engineering, Naval University of Engineering, Wuhan 430033， Hubei, China;2.Aviation Key Laboratory of Science and Technology on Inertia, Xi’an 710061, Shaanxi, China)

A control model of triaxial rotating inertial navigation system (RINS) is established to reduce the influence of carrier movement on the error modulation. A reasonable coordinate system is defined based on the triaxial frame structure, and then the transfer process of the carrier motion from the base to initial measurement unit (IMU) is analyzed to find the mathematical relationship between carrier motion and IMU motion. A dynamic model of triaxial frame motion, motor torque and carrier transport power is established based on Euler dynamic equation. A dynamic model of triaxial frame motion，motor torque and carrier motion is established according to Euler dynamic equation. And a control model of triaxial RINS under the condition of carrier motion isolation is established by using the proposed dynamic model and the motion transfer process. Accordingly, the analytical form of real-time change in rotary inertia on the outer ring axis is obtained, which is verified by simulation and actual test.

control science and technology; inertial navigation； rotation control; dynamic model; rotating inertial navigation system

2016-12-08

国家自然科学基金项目(61503404、41404002)；国家重大科学仪器开发专项项目(2011yq12004502)； 航空科学基金项目(20150816002)；海军工程大学自主立项基金项目(20161577、425517K256)

査峰(1984—), 男，讲师, 博士。E-mail: zha_feng@126.com

U666.12+4

A

1000-1093(2017)08-1610-09

10.3969/j.issn.1000-1093.2017.08.020