6R焊接机器人逆解算法与焊接轨迹误差分析
2017-08-31韩兴国宋小辉陈海军殷国富
韩兴国 宋小辉 殷 鸣 陈海军 殷国富
(1.四川大学制造科学与工程学院, 成都 610065; 2.桂林航天工业学院机械工程学院, 桂林 541004;3.南安普顿大学环境与工程学院, 南安普顿 SO17 1BJ)
6R焊接机器人逆解算法与焊接轨迹误差分析
韩兴国1,2宋小辉2,3殷 鸣1陈海军1殷国富1
(1.四川大学制造科学与工程学院, 成都 610065; 2.桂林航天工业学院机械工程学院, 桂林 541004;3.南安普顿大学环境与工程学院, 南安普顿 SO17 1BJ)
为了提高6R焊接机器人的位姿精度和焊接轨迹的准确度,提出了一种基于RBF神经网络的6R焊接机器人逆运动学求解方法。针对6R焊接机器人逆运动学方程组具有高维、非线性、求解复杂的特点,基于RBF神经网络建立运动学逆解预测模型,采用尺度空间理论对焊接机器人的位姿参数样本所在的工作空间进行分区,采用均匀设计法和模糊聚类理论对分区后的训练样本进行优选,并根据Z-Y-Z坐标转换原理进行转换和归一化处理,将逆运动学求解问题转换为基于RBF的6输入6输出预测系统。运用该系统对6R焊接机器人进行了复杂焊接轨迹仿真和点焊实验,并与基于组合优化迭代法和BP神经网络的逆运动学求解效果与焊接精度进行了比较,结果表明,基于RBF的6R焊接机器人运动学逆解预测模型具有求解简单、精度高、便于轨迹规划的特点,证明了该方法的可行性和有效性。
6R焊接机器人; 逆运动学; RBF神经网络; 焊接轨迹; 误差分析
引言
焊接机器人是现代制造业中的一种重要机电一体化设备,己广泛应用于各个行业,其中约90%是6R机器人[1]。由于被焊接零件的多样化,6R焊接机器人需根据制造任务的变化迅速进行相应的调整,以适应不同复杂形状下的焊接轨迹规划任务。对6R机器人而言,运动学和动力学问题一直是研究的热点,而其逆运动学的求解精度是决定焊接机器人焊接轨迹规划精度和效率的一个重要因素[2]。
6R焊接机器人逆运动学求解是焊接机器人焊接轨迹规划的基础和前提,其逆运动学方程组具有高维、非线性的特点,求解复杂且不易求出。6R机器人的逆运动学求解有一些方法,如代数法[3-7]、几何法[8-9]和数值迭代法[10-13]等。这些方法虽然取得了一些成功的应用,但仍有一些局限性,代数法的缺点是计算量大,几何法只适用于一些特殊结构的机器人,数值迭代方法受初始值影响,具有有限的收敛速度,进行实时控制时可靠性低。
神经网络作为一种智能算法,能在一个有限集内和任意精度下逼近任何非线性函数。不少学者在运用神经网络进行6R机器人逆运动学求解方面进行了研究工作,并取得了不错的效果[14-16]。本文采用基于RBF神经网络求解6R焊接机器人的逆运动学方程,并运用此方法对复杂焊接轨迹进行仿真和点焊实验。
1 6R焊接机器人运动学模型
焊接机器人的各关节轴主要包括转动副和移动副,KR16-2型焊接机器人属于6R机器人,本文以该机器人为例进行运动学分析,它的6个运动副全是转动轴,其前3个轴用来确定焊枪在空间中的位置,后3个轴确定焊枪所处的姿态,其结构示意图如图1所示。
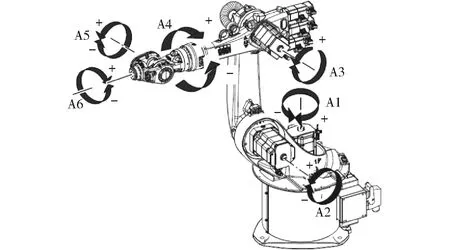
图1 KR16-2型机器人结构示意图Fig.1 Structure diagram of KR16-2 robot
根据KR16-2型焊接机器人的结构参数和外形尺寸,运用D-H参数法建立该机器人的6轴空间坐标系,如图2所示,相邻两轴坐标系的齐次变换矩阵为
(i=1,2,…,n)
(1)
式中θi——关节转角di——连杆偏距αi-1——连杆扭角ai-1——连杆长度
其中ci=cosθi,si=sinθi,sαi-1=sinαi-1,cαi-1=cosαi-1,R16-2型焊接机器人D-H参数如表1所示。

表1 KR16-2型焊接机器人D-H参数Tab.1 D-H parameters of KR16-2 welding robot

图2 KR16-2型焊接机器人D-H坐标系Fig.2 D-H coordinates of KR16-2 welding robot
根据文献[17],KR16-2型焊接机器人末端关节坐标系相对于基础坐标系的坐标转换矩阵为
(2)
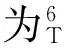
(3)

根据式(1)和式(2)可得
(4)
其中
式中Pn——KR16-2型焊接机器人末端位置En——KR16-2型焊接机器人末端姿态n——法向向量o——滑动向量a——接近向量
根据表1 中的参数,经过运算处理,可得
nx=c23c5-s23c4s5
(5)
ox=s23s4c6+(c23s5+s23c4c5)s6
(6)
ax=-s23s4s6+(c23s5+s23c4c5)c6
(7)
Px=c23d4+s23a3+s2a2
(8)
ny=s1s23c5+(c1s4+s1c23c4)s5
(9)
oy=(c1c4-s1c23s4)c6+[s1s23s5-(c1s4+
s1c23c4)c5]s6
(10)
ay=(s1c23s4-c1c4)s6+[s1s23s5-(c1s4+
s1c23c4)c5]c6
(11)
Py=s1s23d4-s1c23a3-s1c2a2-s1a1
(12)
nz=-c1s23c5-(c1c23c4-s1s4)s5
(13)
oz=(s1c4+c1c23s4)c6+[-c6s23s5+(-s1s4+
c1c23c4)c5]s6
(14)
az=-(s1c4+c1c23s4)s6+[-c1s23s5+
(c1c23c4-s1s4)c5]c6
(15)
Pz=-c1s23d4+c1c23a3+c1c2a2+c1a1
(16)
在式(5)~(16)中,sij=sin(θi+θj),cij=cos(θi+θj)。
对KR16-2型焊接机器人进行逆运动学求解,需要对式(5)~(16)进行求解,求解非常困难,因此考虑使用RBF神经网络对方程组进行逼近。考虑式(4)中的姿态En和位置Pn共有12个变量,作为RBF模型的输入变量太多,设定姿态En按Z-Y-Z轴的旋转顺序进行欧拉变换获得,末端姿态En中的9个变量可以用欧拉角α、β、γ表示,把Px、Py、Pz、α、β、γ作为RBF模型的输入变量。根据坐标转换原理[17],求得机器人末端姿态En按Z-Y-Z旋转的欧拉角为
α=arctan(ay,ax)
(17)
β=arctan(axcosα+aysinα,az)
(18)
γ=arctan(-nxsinα+nycosα,oycosα-oxsinα)
(19)
2 基于RBF的逆解预测模型
2.1RBF神经网络结构
RBF神经网络的结构主要包括输入层、隐含层和输出层,其结构如图3所示。假设RBF神经网络的输入变量为x,x=[x1x2…xn]T∈Rn,输出变量为y,y=[y1y2…ym]T∈Rm,x和y分别是一个n维向量和m维向量,x和y的关系为
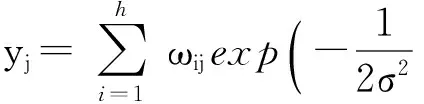
(1≤j≤m)
(20)

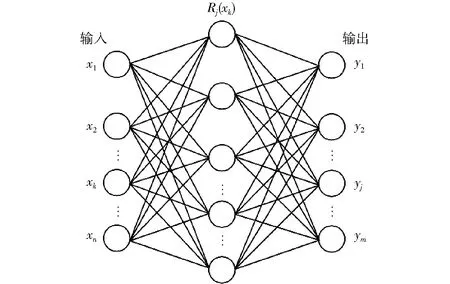
图3 RBF神经网络Fig.3 RBF neural network
假设RBF神经网络的样本总数为N,其预测求解的实质是寻找一组最优的径向基函数的节点中心ci(1≤i≤h)和一组最优的输出权值,使RBF神经网络能够在给定样本输入的情况下,预测的输出值在给定精度下最大限度地接近于实际输出。
2.2 样本数据的优选
在进行基于RBF神经网络的6R焊接机器人逆运动学求解时,必须选择训练样本,训练样本主要是用来训练网络,调整网络的连接权值,使网络的输出与实际输出的误差达到最小,训练样本的选择能够影响神经网络的学习和泛化能力,从而影响最终的求解精度,所以,合理选择训练样本是非常重要的一个环节。
KR16-2型焊接机器人的逆运动学求解的训练样本,可以通过正运动学公式获取,只要已知任意的关节角θ1、θ2、θ3、θ4、θ5、θ6,通过式(8)、(12)、(16)~(19),可以获取相应的位姿变量Px、Py、Pz、α、β和γ,因此,可以按一定的角度间隔,规律地选取关节角,从而确定位姿变量,对于KR16-2型焊接机器人,各轴关节角的约束条件如表2所示。

表2 各轴关节角约束条件Tab.2 Constraint conditions of joint angles
假设选取各关节角间隔为θa,单位为弧度,各关节角每隔θa选取样本,可得总样本数为
(21)
式中θiup——关节角θi约束上限θidown——关节角θi约束下限
当选取训练样本时,假设各关节角的间隔角度θa=0.5时,由式(21)可得,Na=5 118 750。可见,采用该方法选取的训练样本数量较大,可能存在冗余样本,如果以此作为训练样本,训练时间较长,因此,需对训练样本进行优选。首先采用尺度空间理论[18]对6R焊接机器人的工作空间区域进行划分,划分后的工作区域包含3类,即频繁工作区域、临界区域和非工作区域,除去非工作区域的训练样本点,将工作空间区域划分成m个模糊区域,m个区域的训练样本集为Xi(i=1,2,…,m)。然后,采用模糊聚类理论[19-20]的思想寻求每一个工作区域的聚类中心,并以此为基础进行样本优选。
根据模糊C均值(Fuzzy C-meams,FCM)算法,求取每一个模糊区域的聚类中心vi(i=1,2,…,m),使得目标函数达到最小,目标函数及约束条件为
(22)
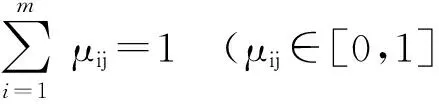
(23)
其中
(24)
(25)
式中μij——第j个对象属于第i个聚类中心的隶属度,每个对象与相应聚类中心的隶属度构成了隶属矩阵U
vi——第i个聚类中心
dij——第i个中心与第j个对象的欧几里德距离
c——加权指数,c∈[1,∞]
由式(22)~(25)可以获得各区域的聚类中心,采用均匀设计法[21]进行样本优选。其步骤为:
(1)根据尺度空间理论将焊接机器人工作空间划分为m个区域,采用分区聚类理论确定各区域的模糊中心。
(2)根据各个区域的关节角及位姿变量的变化范围,合理选择各区域的均匀设计表。
(3)对各区域的样本数据进行预处理,去除冗余样本和可能存在的矛盾样本,确定各个区域的试验点,减少样本总的容量。
(4)在每一个区域,以相应的试验点为中心,根据聚类理论对该区域的样本数据进行分类。
(5)在每一个区域,找到样本点最少的一类,该区域样本个数为Hi(1≤i≤m)。
(6)将各个区域的样本综合在一起,组成总的训练样本,样本个数为H=H1+H2+…+Hm。
提出的基于RBF神经网络的6R焊接机器人逆运动学求解方法采用在线训练,通过对样本进行优选,减少总样本点的个数,从而减少在线计算量,提高系统的收敛速度和实时性。
2.3 样本参数归一化处理
为了提高预测模型的计算效率,避免在计算过程中发生数据溢出的现象,对样本的输入输出参数进行归一化处理是非常必要的,经归一化处理后的样本参数在0~1范围之间,归一化处理公式为
(26)
式中z——归一化前参数zmin——参数最小值zmax——参数最大值z′——归一化后的参数
2.4 6R焊接机器人逆解预测模型
根据分区聚类理论和均匀设计思想,在KR16-2型焊接机器人的工作范围内优选出约8 000个点作为训练样本,优选的样本点分布均匀。将训练样本位姿参数经过式(26)归一化处理后作为RBF的输入参数,即x=[P′xP′yP′zα′β′γ′]T,将关节角经过式(26)归一化处理后作为RBF的输出参数,即y=[θ′1θ′2θ′3θ′4θ′5θ′6]T,建立基于RBF神经网络的6输入6输出的逆运动学求解预测模型,用约8 000个点的样本对该预测模型进行训练。
已知位姿参数,用该预测模型计算出的关节角是0~1之间的数,需要进行反归一化处理,即
θj=θjmin+θ′j(θjmax-θjmin) (j=1,2,…,6)
(27)
式中θ′j——经归一化处理后预测的输出关节角
3 焊接轨迹仿真与误差分析
3.1 运动轨迹
根据KR16-2 型焊接机器人的结构参数,运用Matlab软件建立其物理模型,根据运动学模型,使机器人末端工具模拟仿真一段椭圆线,如图4所示。

图4 KR16-2型机器人焊接轨迹仿真Fig.4 Welding track simulation of KR16-2 robot
在图4所示的椭圆线轨迹上,选30个点作为焊点位置, 并确立这些点对应的机器人末端位姿,由式(8)、(12)、(16)~(19)可得30组Px、Py、Pz、α、β和γ,经归一化处理后以其作为RBF预测模型的测试数据,可得30组预测输出值。
3.2 逆解模型预测效果评定
为了客观地评定该模型的预测效果,采用绝对误差和均方根误差评价指标进行评判,即
eim=|θPim-θTim|
(i=1,2,…,6;m=1,2,…,30)
(28)
(29)
式中N——测试样本数,取30θPim——输出的预测关节角θTim——某一工作位置的关节角理论值
根据式(28)求得各关节角在30个焊点位置的绝对误差值如图5和图6所示,关节角θ1、θ2、θ3、θ4、θ5、θ6最小绝对误差分别为6.3×10-5、7.2×10-5、5.5×10-5、7.9×10-5、6.3×10-5、8.9×10-5rad,最大绝对误差分别为2.99×10-4、3.21×10-4、2.87×10-4、2.48×10-4、2.86×10-4、3.07×10-4rad。根据式(29)可求得关节角θ1、θ2、θ3、θ4、θ5、θ6的均方根误差为2.05×10-4、2.24×10-4、1.88×10-4、1.79×10-4、1.94×10-4、1.97×10-4rad。可以看出,基于RBF神经网络建立的6R焊接机器人逆解预测模型的预测精度很高,在30个焊点位置的预测误差变化不大。

图5 前三轴关节角的绝对误差Fig.5 Absolute errors of joint angle for the first three axes
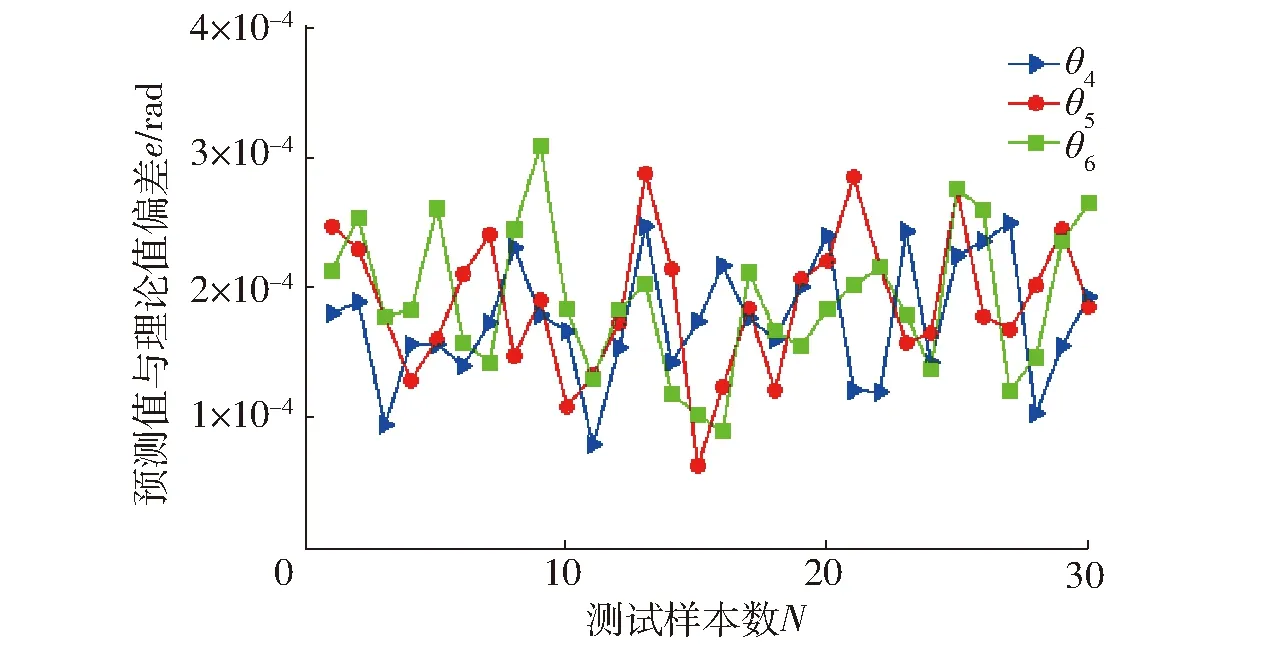
图6 后三轴关节角的绝对误差Fig.6 Absolute errors of joint angle for the latter three axes
为了对基于RBF神经网络的KR16-2型焊接机器人逆运动学求解预测方法的可行性和精度进行客观评价,将该方法与文献[13](基于一种组合优化的迭代法)和文献[15](基于BP神经网络)中的逆运动学求解方法进行比较,如表3所示。通过表3可看出,3种方法都具有较高的预测精度,但采用基于RBF神经网络的预测模型具有更高的求解精度,泛化能力更强、鲁棒性更优。

表3 KR16-2焊接机器人逆解Tab.3 Results of inverse kinematics for KR16-2 robot (°)
4 实验论证
为了验证该逆运动求解方法的可行性和准确度,在钢制板类零件上进行焊接实验,零件尺寸为300 mm×200 mm,在零件的椭圆线轨迹上,选8个点作为焊接轨迹对应的焊点位置,如图7a所示。采用本文提出的基于RBF神经网络的6R焊接机器人逆运动学求解方法,在图8所示的焊接机器人实验平台上,逐一对该零件上各焊点进行点焊实验,焊接后零件如图7b所示。采用激光跟踪仪对焊接后零件焊点中心位置进行测量,可得椭圆轨迹上8个焊点位置的x轴、y轴、z轴的坐标值,焊点位置的坐标误差为
ewn=|pwpm-pwtm| (m=1,2,…,8)
(30)
式中m——焊点编号w——x、y或z坐标ewm——在第m个焊点位置上,采用本文方法x(y或z)坐标值与其理论值之差
pwpm——测量所得第m个焊点位置的x(y或z)坐标值
pwtm——第m个焊点位置上的x(y或z)坐标的理论值

图9 焊接工件上焊点的各坐标误差Fig.9 Relevant coordinate errors of some welding spots on welding part

图7 焊接工件图Fig.7 Welding workpiece
分别采用基于一种组合优化迭代方法[13]和基于BP神经网络[15]的6R焊接机器人逆运动学求解方法,对图7a所示零件椭圆轨迹上8个焊点逐一进行点焊实验,采用激光跟踪仪测量8个焊点位置中心的空间坐标,利用式(30)求x、y、z坐标的误差,采用3种方法所计算的焊接轨迹焊点位置的x、y、z坐标误差如图9所示。

图8 焊接机器人实验平台Fig.8 Experiment platform of welding robot
为了研究焊接轨迹精度,焊接轨迹上各焊点的位置误差公式为
(31)
式中epm——焊接轨迹上第m个焊点的位置误差
对基于RBF、BP和组合优化迭代进行6R焊接机器人逆运动学求解方法,根据所测的各焊点的位置坐标,由式(31)求出3种方法所对应的位置误差,如图10所示。为了客观地评价基于3种方法的焊接精度,对3种方法焊点位置的坐标误差和位置误差进行比较,如表4所示。由图9、10和表4可以看出,基于RBF神经网络逆运动求解方法的焊接轨迹坐标误差和位置误差最小,其焊点位置的x、y、z坐标平均误差分别为0.020 5、0.018 9、0.022 0 mm;焊点位置平均误差为0.038 1 mm。基于BP神经网络和组合优化迭代法的逆运动学求解算法的焊点位置x、y、z坐标平均误差分别为0.029 2、0.029 0、0.027 5 mm和0.032 8、0.029 9、0.030 5 mm;其焊点位置平均误差分别为0.050 6 mm和0.054 9 mm。由此可见,采用基于RBF神经网络的逆运动学求解方法具有更高的求解精度。
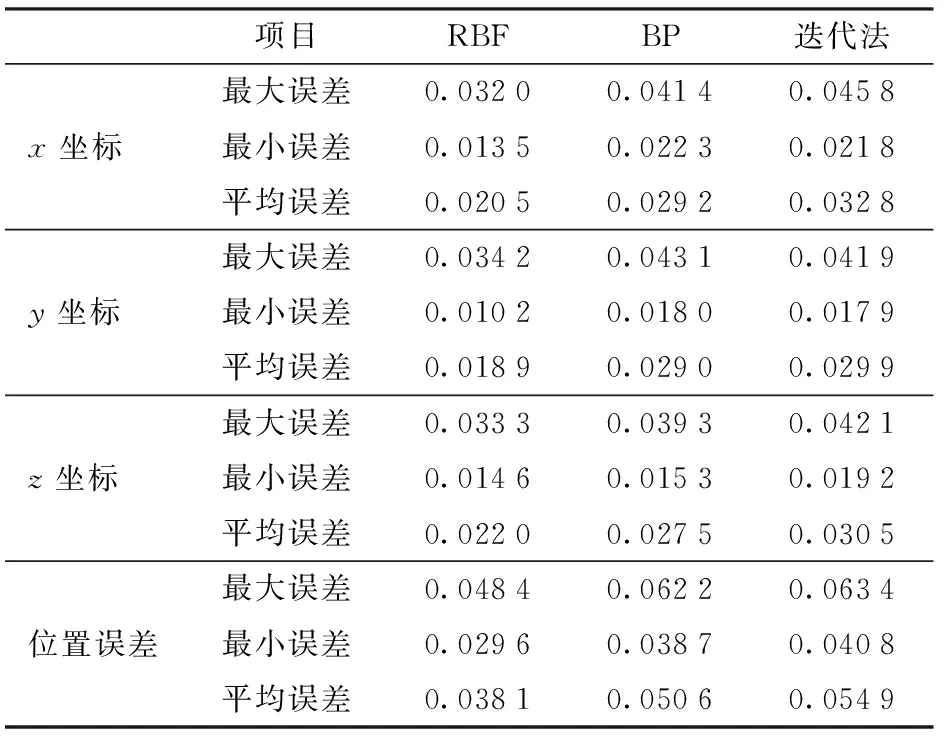
表4 坐标误差和位置误差对比Tab.4 Comparison of coordinate and position errors mm
5 结论
(1)提出了一种基于RBF的6R焊接机器人逆运动学求解方法,该方法求解简单,求解精度较高,可应用于其他一般6R焊接机器人,提高焊接轨迹的准确度。
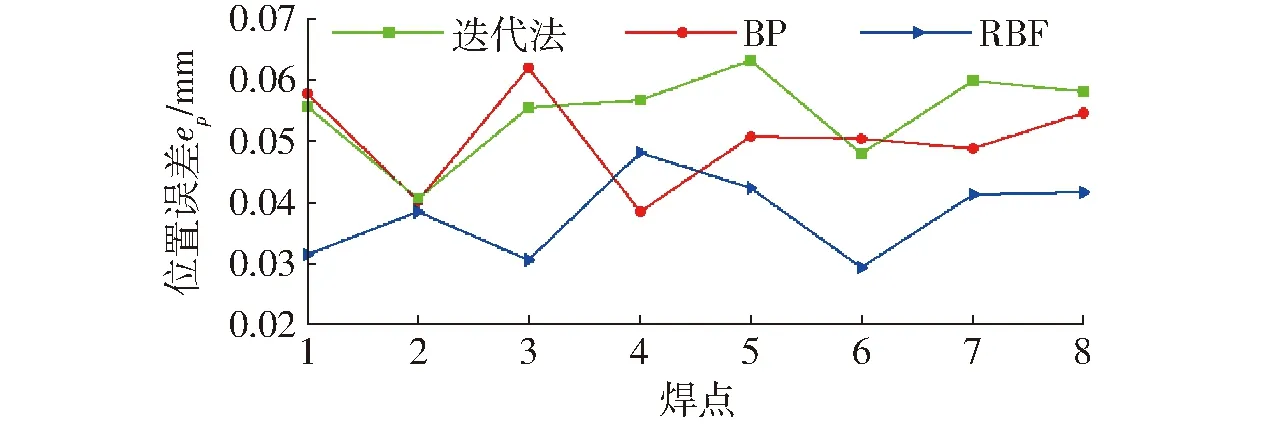
图10 焊接工件上各焊点的位置误差Fig.10 Position errors of some welding spots on welding part
(2)基于RBF的6R焊接机器人逆运动学预测模型预测精度高,具有较强的泛化能力;经过焊接轨迹仿真及误差分析论证,与基于组合优化迭代和基于BP神经网络预测模型进行比较,基于 RBF的预测模型具有更好的鲁棒性和准确性。
(3) 采用基于RBF的6R焊接机器人逆运动学求解方法进行点焊实验及误差分析,求解焊接轨迹上所选焊点的坐标误差和位置误差,并与基于组合优化迭代和基于BP神经网络的逆运动学求解方法进行比较,结果表明,基于RBF的6R焊接机器人逆运动学求解方法的坐标误差和位置误差更小。
1 李雪琴, 蒋红海, 殷国富,等. 多关节焊接机器人轨迹误差补偿解耦分析[J]. 焊接学报, 2013,34(10):63-66. LI Xueqin, JIANG Honghai, YIN Guofu, et al. Research on decoupling of trajectory error compensation for multi-joint welding robot[J]. Transactions of the China Welding Institution, 2013,34(10):63-66. (in Chinese)
2 丁长涛,杨世锡,甘春标. 随机不确定扰动诱发的机器人动力学行为及其优化[J/OL]. 农业机械学报,2016, 47(8):356-363, 398. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160847&flag=1.DOI:10.6041/j.issn.1000-1298.2016.08.047. DING Changtao, YANG Shixi, GAN Chunbiao. Dynamic behavior and its optimization of robot under randomly uncertain disturbance[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(8):356-363,398.(in Chinese)
3 LEE H Y, LIANG C G. A new vector theory for the analysis of spatial mechanisms[J]. Mechanisms and Machine Theory, 1988, 23(3):209-217.
4 刘松国, 朱世强, 王宣银. 基于矩阵分解的一般6R机器人实时高精度逆运动学算法[J]. 机械工程学报, 2008, 44(11): 304-309. LIU Songguo, ZHU Shiqiang, WANG Xuanyin. Rea-time and high-accurate inverse kinematics algorithm for general 6R robots based on matrix decomposition[J]. Chinese Journal of Mechanical Engineering,2008, 44(11): 304-309. (in Chinese)
5 吕世增, 张大卫, 刘海年.基于吴方法的6R机器人逆运动学旋量方程求解[J]. 机械工程学报, 2010, 46(17):35-41. LÜ Shizeng, ZHANG Dawei, LIU Hainian. Solution of screw equation for inverse kinematics of 6R robot based on wu’s method[J]. Journal of Mechanical Engineering,2010, 46(17):35-41. (in Chinese)
6 刘华山, 朱世强, 吴剑波.基于向量内积的机器人实时逆解算法[J].农业机械学报,2009, 40(6):212-216. LIU Huashan, ZHU Shiqiang, WU Jianbo. Real-time inverse kinematics algorithm based on vector dot product[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(6): 212-216. (in Chinese)
7 HUSTY M L, PFUMER M, SCHROCKER H P. A new and efficient algorithm for the inverse kinematics of a general serial 6R manipulator[J].Mechanism and Machine Theory, 2007, 42(1): 66-81.
8 邱宁佳, 隋振, 李明哲, 等. 六自由度机器人空间划线轨迹规划算法[J].吉林大学学报:工学版, 2013,43(5):1307-1313. QIU Ningjia, SUI Zhen, LI Mingzhe, et al. Algorithm of 6-DOF robot trajectory planning applied to special marking[J]. Journal of Jilin University: Engineering and Technology Edition, 2013,43(5): 1307-1313. (in Chinese)
9 李宪华, 郭永存, 张军, 等. 模块化六自由度机械臂逆运动学解算与验证[J/OL]. 农业机械学报, 2013,44(4):246-251. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20130443&flag=1.DOI:10.6041/j.issn.1000-1298.2013.04.043. LI Xianhua, GUO Yongcun, ZHANG Jun, et, al. Inverse kinematics solution and verification of modular 6-DOF manipulator[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(4): 246-251.(in Chinese)10 GOLDENBERG A A, BENHABIB B, FENTON R G. A complete generalized solution to the inverse kinematics of robots[J]. IEEE Journal of Robotics and Automation,1985,1(1): 14-20.
11 ANGELES J. On the numerical solution of the inverse kinematic problem[J]. International Journal of Robotics Research, 1985, 4(2):21-37.
12 LENARCIC J. An efficient numerical approach for calculating the inverse kinematics for robot manipulators[J]. Robotics,1984, 3(1):21-26.
13 周友行, 张建勋, 董银松. 点焊机器人复杂轨迹逆运动学组合优化求解[J]. 焊接学报,2010,31(9):21-24. ZHOU Youxing, ZHANG Jianxun, DONG Yinsong. An optimization algorithm for combination inverse kinematics problems of welding robot in complex trajectory[J]. Transactions of the China Welding Institution, 2010,31(9):21-24. (in Chinese)
14 KOKER R, OZ C, CAKAR T, et al. A study of neural network based inverse kinematics solution for a three-joint robot[J]. Robotics and Autonomous Systems, 2004, 49(3-4): 227-234.
15 KARLIK B, AYDIN S. An improved approach to the solution of inverse kinematics problems for robot manipulators[J]. Engineering Applications of Artificial Intelligence, 2000, 13(2):159-164.
16 KOKER R. A genetic algorithm approach to a neural- network-based inverse kinematics solution of robotic manipulators based on error minimization[J]. Information Sciences, 2012, 222(1): 81-87.
17 蔡自兴. 机器人学[M]. 北京:清华大学出版社,2009.
18 骆剑承,周成虎,梁怡,等. 多尺度空间单元区域划分方法[J]. 地理学报,2002, 57(2): 167-173. LUO Jiancheng, ZHOU Chenghu, LIANG Yi, et al. Scale-space theory based regionalization for spatial cells[J]. Acta Geographica Sinica, 2002, 57(2): 167-173. (in Chinese)
19 周世波, 徐维祥, 柴田. 基于数据加权策略的模糊C均值聚类算法[J]. 系统工程与电子技术, 2014,36(11):2314-2319. ZHOU Shibo, XU Weixiang, CHAI Tian. Fuzzy C-means clustering algorithm based on the strategy of data weighted[J]. Systems Engineering and Electronics, 2014, 36(11): 2314-2319. (in Chinese)
20 高新波.模糊聚类分析及其应用[M].西安:西安电子科技大学出版社,2004.
21 马翔, 陈新楚,王劭伯. 均匀设计法在RBF神经网络样本优选中的应用[J]. 模式识别与人工智能, 2005, 18(2): 252-255. MA Xiang, CHEN Xinchu, WANG Shaobo. Application of the uniform design to the optimal selection of samples for RBF neural networks[J]. Pattem Recognition and Aitificial Intelligence, 2005, 18(2): 252-255. (in Chinese)
Solution of Inverse Kinematics and Welding Trajectory Error Analysis for 6R Welding Robot
HAN Xingguo1,2SONG Xiaohui2,3YIN Ming1CHEN Haijun1YIN Guofu1
(1.SchoolofManufacturingScienceandEngineering,SichuanUniversity,Chengdu610065,China2.CollegeofMechanicalEngineering,GuilinUniversityofAerospaceTechnology,Guilin541004,China3.FacultyofEngineeringandEnvironment,UniversityofSouthampton,SouthamptonSO17 1BJ,UnitedKingdom)
A new method of solving inverse kinematics of 6R welding robot based on radial basis function(RBF) neural networks was presented to improve the precision of the position and orientation and the accuracy of welding trajectory for the 6R welding robot. The inverse kinematics solution prediction model of the 6R welding robot was established based on RBF neural networks because the inverse kinematics equations were high-dimensionally nonlinear and solving these equations was complex. The work space in which 6R welding robot position and orientation sample parameters were situated was divided based on scale-space theory. After that the training sample set was selected optimally based on uniform design and the cluster theory. The parameters were transformed and normalized according to theZ-Y-Zcoordinate conversion principle. The problem of solving the inverse kinematics equations was transformed into six inputs and six outputs prediction system based on RBF neural network. Complex movement trajectory of 6R robot was simulated and the spot welding experiments were done by means of this prediction system. The results of the prediction and welding track accuracy were compared with the inverse kinematics solution based on combinatorial optimization iteration algorithm and back propagation (BP) neural networks. The results showed that the RBF prediction model of solving 6R welding robot inverse kinematics equations was simpler, more accurate and easier to do trajectory planning, and it was proved to be feasible and effective.
6R welding robot; inverse kinematics; radial basis function neural networks; welding trajectory; error analysis
10.6041/j.issn.1000-1298.2017.08.046
2016-11-20
2017-03-03
“十二五”国家科技支撑计划项目 (2015BAF27B01)、四川省科技计划项目(2015GZ0036、2016GZ0195)、广西高校中青年教师基础能力提升项目(KY2016YB535)和广西高校机器人与焊接重点实验室主任基金项目(JQR2015ZR04)
韩兴国(1981—),男,博士生,桂林航天工业学院副教授,主要从事机电一体化技术研究,E-mail: hanxingguo2004@163.com
殷国富(1956—),男,教授,博士生导师,主要从事CAD/CAM、智能制造及装备研究,E-mail: gfyin@scu.edu.cn
TP242
A
1000-1298(2017)08-0384-07
