轮-腿复合移动机器人RUPU-RUPR球面并联腿机构动力学研究

桑董辉 陈 原 高 军

(山东大学(威海)机电与信息工程学院， 威海 264209)

轮-腿复合移动机器人RUPU-RUPR球面并联腿机构动力学研究

桑董辉 陈 原 高 军

(山东大学(威海)机电与信息工程学院， 威海 264209)

提出了一种二自由度球面并联腿机构，并以该机构为基础，设计了一种结构简单且越障性能良好的轮-腿复合移动机器人。阐述了该机构的组成，采用解析几何法和闭环约束方程构建了RUPU-RUPR球面并联腿机构的位置逆解、工作空间、速度和加速度模型,并验证了其准确性。运用牛顿-欧拉法建立了RUPU-RUPR球面并联腿机构的动力学模型。在给定动平台的运动规律和外力后，通过动力学方程求解出RUPR驱动支链驱动力，RUPU驱动支链驱动力矩以及RUPR驱动支链约束力矩，并给出动力学模型仿真解。结果表明该机构具有良好的工作性能。

轮-腿复合移动机器人； 球面并联机构； 动力学模型

引言

从行进机构的拓扑构型角度，可将移动机器人分为轮式、腿式、履带式和复合式4种类型[1-3]。轮式移动机构应用最为普遍，其结构简单、移动速度快，但在特殊环境下越障能力差。由仿生学发展而来的腿式移动机构行走时与地面接触为不连续的离散点，适合于攀爬和跨越简单障碍，而对于复杂崎岖的地形也存在局限性。履带式移动机构支撑面积大、接地比压小，适合在松软的路面行走，但履带式机器人存在行动速度慢、振动大、灵活性不足等缺陷。为了适应复杂的陆地环境，目前很多机器人都采用复合移动机构。其中，轮-腿复合式移动机器人[4-7]兼具轮式机器人的稳定性好和腿式机器人的越障能力强的优点，受到国内外学者的广泛关注[8-10]。

目前，轮-腿复合式移动机构的构型研究仅局限于串联机构[11-16]。串联式轮-腿复合移动机构虽然具有良好的越障性能，但存在驱动关节多、控制难度大、运动姿态单调和刚度差等缺陷。与串联腿机构相比，并联腿机构具有控制简单、姿态调整丰富且刚度高的优点，它可根据机器人移动操纵任务要求产生其他多维方向上的轮子空间姿态调整运动。但现有的多自由度并联机构自由度过多，且整体安装模块大，在结构上很难应用于轮-腿复合式移动机器人的腿部机构。球面并联机构[17-24]的工作空间大且连续性强，能使安装于动平台上的轮子到达球面空间内的任意位置，这样会大大提高机器人在复杂多变环境下的越障灵活性。但现有的球面并联机构大多具有3条支链以上，且自由度多、控制困难。为了提高复杂环境下移动机器人的越障性能,本文提出RUPU-RUPR二自由度球面并联腿机构。基于该球面并联机构，设计一种可以实现灵活越障功能的轮-腿复合式移动机器人。并对RUPU-RUPR并联机构进行运动学和动力学建模分析。

1 RUPU-RUPR球面并联腿机构

1.1 RUPU-RUPR球面并联腿机构设计

如图1所示为轮-腿复合式移动机器人的RUPU-RUPR球面并联腿机构。该机构由动平台、静平台、RUR传动支链和两条驱动支链构成。转动副6、万向节5、移动副4和万向节3构成了RUPU驱动支链。转动副9、万向节10、移动副11(用螺旋副代替，采用电机驱动)和转动副1构成了RUPR驱动支链。中间RUR传动支链由转动副7、万向节8和转动副2构成。

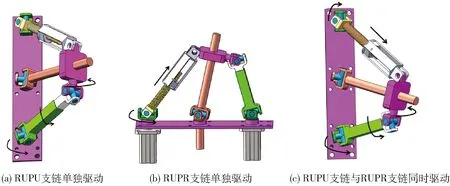
图2 RUPU-RUPR球面并联腿机构的运动姿态Fig.2 Motion gestures of RUPU-RUPR spherical parallel mechanism

图1 RUPU-RUPR球面并联腿机构Fig.1 RUPU-RUPR spherical parallel mechanism1、2、6、7、9.转动副 3、5、8、10.万向节 4.移动副 11.螺旋副

1.2 RUPU-RUPR球面并联腿机构运动特性

RUPU驱动支链是把驱动电机的扭矩通过转动副6、万向节5、移动副4(该移动副截面为四边形，可以传递扭矩)和万向节3把扭矩传递到动平台，以实现如图2a所示的动平台绕Y轴的旋转。RUPR驱动支链把驱动电机的扭矩通过转动副9、万向节10传递到螺旋副11，实现如图2b所示的动平台绕X轴方向的旋转。2条支链同时作用时，机构姿态如图2c所示。RUR传动支链通过转动副7、万向节8和转动副2把输出扭矩传递到轮子，实现轮子的旋转运动。通过调整2条驱动支链的驱动电机的转速和转向，可使动平台到达以RUR传动支链长度为半径的球面空间中的任一点，实现轮子的灵活转向和越障。

2 轮-腿复合式移动机器人及其越障性能

以RUPU-RUPR球面并联机构作为移动机器人的腿机构，构建了如图3a所示的轮-腿复合式机器人。该机器人结构简单，驱动电机全部布置在躯干内。机器人两侧对称分布4个RUPU-RUPR球面并联机构，机构的动平台连接轮子。为了保证机器人在各种姿态下的平稳运行，防止轮子出现打滑和卡死现象，在对称分布的两个球面并联机构的主轴中间安装有如图3b所示的差速器。

图3 轮-腿复合式移动机器人Fig.3 Wheel-legged mobile robots

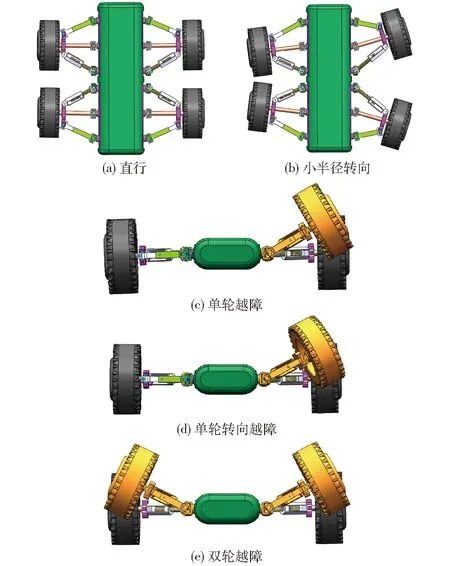
图4 轮-腿复合式移动机器人的越障姿态Fig.4 Obstacle crossing motion gestures of wheel-legged mobile robots

当RUPU-RUPR球面并联机构在其工作空间内进行姿态调整时，可以实现轮-腿复合式机器人的转向以及如图4所示的小半径转向、越障以及转向越障等各种越障姿态。RUPU-RUPR球面并联机构的轮子可以到达其球面工作空间上的任意一点，轮子的角度可以任意调控，从而使轮子具有非常灵活的越障性能。

3 RUPU-RUPR球面并联机构的运动学建模

RUPU-RUPR球面并联机构的运动学建模是在动平台姿态角已知的情况下，求两条驱动支链的伸缩位移、伸缩速度、旋转角速度、伸缩加速度以及动平台的角速度。在进行运动学建模之前，首先建立如图5a所示的坐标系，在静平台上建立固定坐标系{A}(OXYZ)，其坐标原点建立在静平台中心O处，X轴垂直于A1A2，Y轴沿A1A2方向，Z轴符合右手定则；同理，在动平台上建立动坐标系{P}(PXPYPZP)。在支链上建立支链坐标系{A1}(A1X1Y1Z1)，该坐标原点在A1处，Z1轴从A1指向B1，Y1轴平行于YZ平面，X1轴符合右手定则。

图5 坐标系及坐标变换Fig.5 Coordinate frame and transformation

3.1 坐标变换与位置逆解

(1)

式中ATP——动坐标系到定坐标系的旋转矩阵

当动平台姿态角为α和β，RUR传动支链OP长度为h时，动坐标系{P}的原点在固定坐标系下的位置向量U为

(2)

其中

式中u——{P}的原点在固定坐标系中位置向量

同理，根据RUPR驱动支链的姿态角θ和φ(θ为支链绕X轴旋转的角度，φ为支链绕Y轴旋转的角度)，可以得到RUPR驱动支链相对于定平台的旋转矩阵为

如图5b所示，为了方便计算假设lOB1=lOA1=R。当动平台绕X轴转过α角度时，RUPR驱动支链转过角度为φ，其中，α为以R为半径的圆的圆心角，φ为以R为半径的圆的圆周角，可得φ=0.5α。

在固定坐标系下，RUPR驱动支链、静平台、动平台和RUR传动轴构成如图5a所示的四边形结构，用向量表示为lOA1+lA1B1=lOP+lPB1，因此，机构的闭环约束方程可以表示为

A1+l1AS1=b1

(3)

其中

式中A1——A1点在固定坐标系中的位置向量l1——向量lA1B1的模AS1——向量lA1B1在固定坐标系下单位向量

b1——B1点在固定坐标系下的位置向量

求解方程(3)得

(4)

式中h1——OB1的长度

向量lA1B1的单位向量在支链坐标系{A1}下表示为

A1S1=[0 0 1]T

在固定坐标系{A}下可表示为

RUPU驱动支链可以把扭矩从电动机直接传递到动平台，所以RUPU驱动支链上转动副6转过的角度γ与动平台绕Y轴转过的角度β一致，即γ=β。联立方程(4)得到RUPU-RUPR球面并联机构的运动学位置逆解为

(5)

当RUPR驱动支链的螺旋副为驱动副(视为移动副计算)时，RUPU驱动支链的移动副起到被动约束作用。由于两条驱动支链的移动副都由缸体和活塞两部分组成，这里假设两条支链的缸体与活塞长度一样，在固定坐标系下缸体和活塞的质心位置向量可表示为

(6)

式中Ar1——缸体质心位置Ar2——活塞质心位置e1——缸体长度e2——活塞长度

3.2 速度与加速度模型构建

根据RUPR驱动支链的运动姿态角θ和φ，以及支链旋转矩阵ATA1，可以求得支链的角速度矢量为

同理，根据动平台的运动姿态角α、β以及动平台相对于固定平台的旋转矩阵ATP，求得动平台的角速度矢量为

式(3)右侧对时间求导，得到固定坐标系下RUPR驱动支链上B1点的速度矢量为

AVB1=Aωb1

(7)

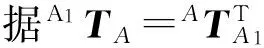
(8)

将式(3)左侧对时间求导，并通过坐标变换也可得支链坐标系下B1点的速度矢量为

(9)

式中A1ω1——支链坐标系下RUPR驱动支链绕A1点转动的角速度矢量

将式(8)代入式(9)并用向量A1S1对式(9)两边作点积可得

(10)

式中A1VB1z——B1点的速度矢量AiVB1在Z方向的分量，即支链的伸缩速度，用支链坐标系下Z方向的移动速度表示

式(6)对时间求导，并通过坐标变换可得到支链坐标系下缸体和活塞的质心速度

(11)

式(7)对时间求导可得固定坐标系下B1点的加速度矢量

(12)

(13)

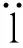
式(13)两边用向量A1S1作点积，可得RUPR驱动支链的伸缩加速度

(14)

式(11)对时间求导，并通过坐标变换得到缸体和活塞的质心加速度矢量

(15)

4 RUPR-RUPU并联机构动力学建模

如图6所示为RUPR-RUPU球面并联机构的受力简图，该机构为二自由度球面并联机构。RUPR驱动支链的驱动电机通过螺旋副把输出的扭矩转化为直线推力，使动平台绕X轴转动。RUPU支链的驱动电机把输出扭矩通过如图1所示的转动副6、万向节5、移动副4和万向节3传递到动平台，使动平台绕Y轴转动。RUPU驱动支链中的移动副起被动约束作用。转动副1限制了动平台的绕Z轴的转动自由度。

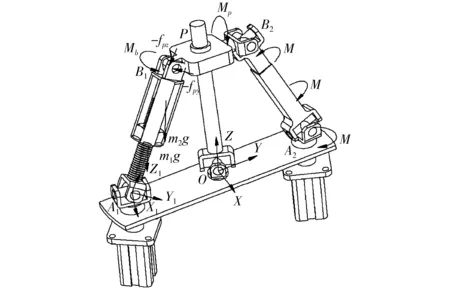
图6 RUPU-RUPR球面并联机构的受力简图Fig.6 Mechanism force diagram of RUPU-RUPR spherical parallel

4.1 支链动力学方程

设fb=[0fpyfpz]T为支链坐标系下RUPR驱动支链作用于动平台的三维力向量，g=[0 0 -g]T为固定坐标系下的重力加速度向量，M为RUPU驱动支链的驱动力矩，Mp为RUPU支链传递到动平台U副上的扭矩，Mbx为RUPR支链所受的扭矩。假设RUPU支链的扭矩传递效率为100%，通过受力分析可以得到RUPR支链的牛顿方程

(16)

式中Fp——动平台所受合外力F——RUPR支链直线驱动力m2——支链活塞质量

RUPR支链在支链坐标系下相对于坐标原点A1的合外力矩向量为

A1MA1=l1A1S1(-fp)+

[m1e1+m2(l1-e2)](A1S1×A1g)+Mb

(17)

其中

A1g=ATA1Tg

式中A1g——支链坐标系下的重力加速度Mb——支链坐标系下动平台作用于RUPR驱动支链的扭矩

m1——支链缸体质量

通过坐标转换得到RUPR支链所受的扭矩Mb

Mb=Rx(θ)Rx(α)Mp

(18)

其中

Rx(α)和Rx(θ)分别为固定坐标系和动坐标系绕Y轴的旋转矩阵。

RUPR驱动支链在其支链坐标系下坐标原点相对A1的合惯性力矩向量为

A1NA1=-m1e1(A1S1iV1)-m2(l1-e2)(A1S1A1V2)-

(19)

式中A1I1、A1I2——缸体和活塞在RUPR支链坐标系下关于质心的惯性矩阵

由欧拉方程得到力矩平衡方程为

A1NA1=A1MA1

(20)

联立式(16)和式(20)得到支链的动力学方程，对其求解可得RUPR驱动支链使动平台绕X轴转动的驱动力

4.2 动平台动力学方程

动平台只具有X、Y方向的旋转运动，因此以固定坐标系原点O为质心建立欧拉方程为

ANp+b1Afp+AMp+Anp=0

(21)

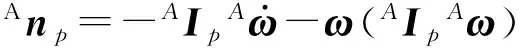
Afp=AiTpfp

(22)

式中Anp——固定坐标系下动平台关于质心的惯性力矩向量

ANp——固定坐标系下动平台所受载荷力矩矢量

Afp——固定坐标系下RUPR驱动支链对动平台的作用力

AMp——固定坐标系下RUPU驱动支链作用于动平台的扭矩

AIp——固定坐标系下动平台关于质心的惯性矩阵

求解方程(21)可得fpz和Mp,将其代入式(16)可求得到驱动力F，联立式(16)、(20)和(22)，可得RUPU-RUPR球面并联机构的动力学模型

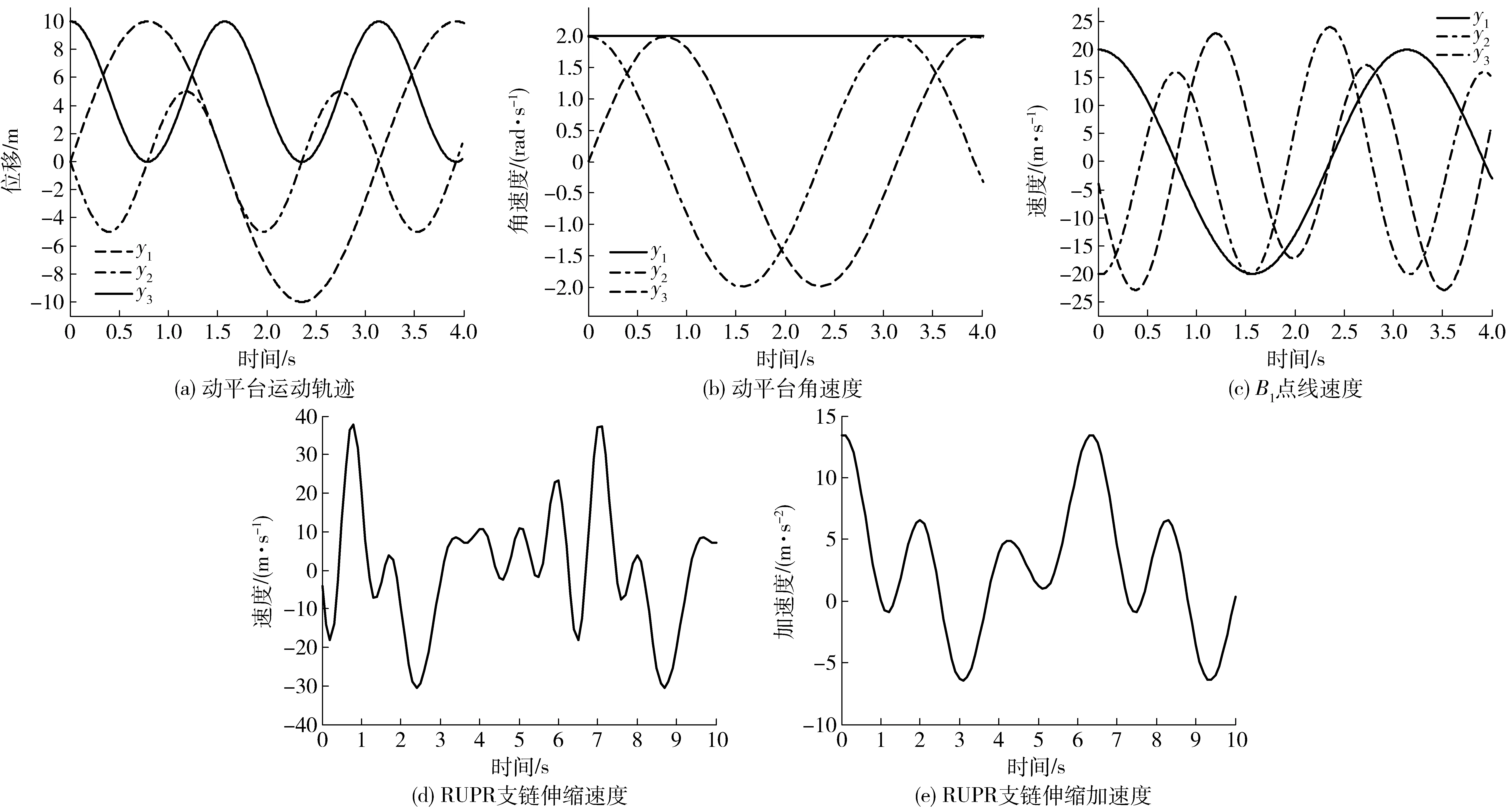
图7 运动学数值仿真结果Fig.7 Numerical simulation results of kinematics

5 RUPU-RUPR球面并联腿机构的算例仿真

经Matlab编程计算，可得动平台和B1点运动轨迹、动平台角速度、B1点线速度、支链伸缩速度、支链伸缩加速度等运动学模型数据。这些运动学数值仿真轨迹曲线如图7所示。另外，通过数值模拟得到如图8所示的动平台工作空间三维图，从图8中可看出该机构工作空间为球面空间的子集。

假设动平台以2 rad/s的速度绕固定坐标系的X轴和Y轴转动。机构质心重力加速度为g=[0 0 -10]T，动平台所受外力为fp=[0 0 0]T，动平台所受载荷力矩矢量为Np=[0 0 0]T。假设2条支链的缸体和活塞质量相同m1=m2=1 kg，动平台质量m设为1 kg。2条支链的转动惯量设为

动平台转动惯量为

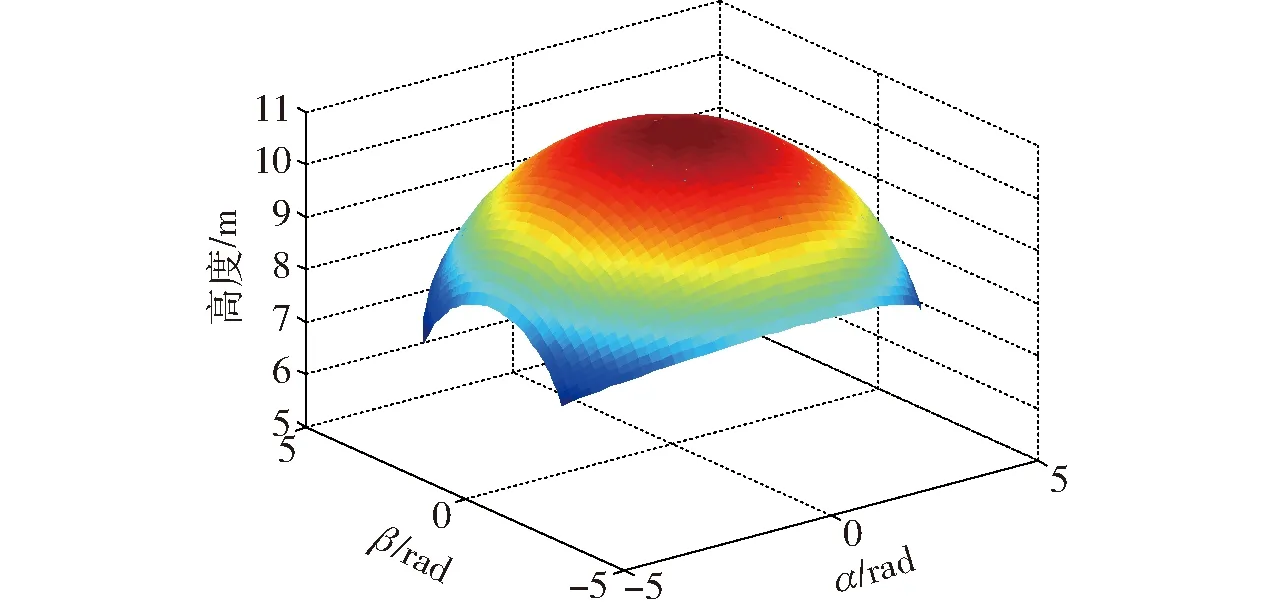
图8 工作空间Fig.8 Workplace

经Matlab编程计算，可得RUPR驱动支链的驱动力，RUPU驱动支链的驱动力矩以及RUPR驱动支链的约束力矩，其仿真曲线如图9所示。从图中可以看出RUPU驱动支链所需的驱动力矩和RUPR

驱动支链所需的约束力矩较小，RUPR驱动支链所需的驱动力较大。为了减少振动和防止过载，根据螺旋副受力

N=F′d/(nπ)

式中N——螺旋副扭矩F′——轴向力n——螺旋副正效率d——导程

选择大导程螺旋副以减少驱动扭矩。这些动力学模型的数值仿真结果可为后续电动机选型和机器人越障性能的分析提供理论指导。

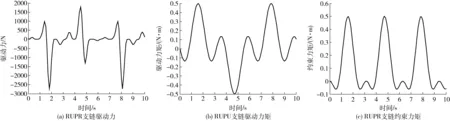
图9 动力学数值仿真结果Fig.9 Numerical simulation results of dynamics

6 结论

(1)提出了一种二自由度球面并联腿机构，该机构结构紧凑，控制灵活，并具有球面工作空间。基于该球面并联机构设计了一种能够实现灵活越障的轮-腿复合移动机器人。

(2)采用解析几何法和闭环约束方程建立了机构的运动学模型，并通过数值模拟验证了位置逆解、速度解、加速度解的正确性，并仿真出机构的工作空间。

(3)基于牛顿-欧拉方程构建了机构的动力学模型，并通过数值仿真计算得出机构的驱动力矩、驱动力和约束力矩，为后续的控制，步态规划以及越障性能分析奠定基础。

1 李磊，叶涛，谭民，等．移动机器人技术研究现状与未来[J]．机器人， 2002， 24(5)： 475-480． LI L, YE T, TAN M, et al. Present state and future development of mobile robot technology research[J]. Robot, 2002, 24(5):475-480.(in Chinese)

2 KALAKRISHNAN M, BUCHLI J, PASTOR P, et al. Learning, planning and control for quadruped locomotion over challenging terrain[J]. International Journal of Robotics Research, 2011, 30(2):236-258.

3 吉爱红，戴振东，周来水．仿生机器人的研究进展[J]．机器人， 2005， 27(3)： 284-288． JI A H, DAI Z D, ZHOU L S. Research development of bioinspired robotics[J]. Robot, 2005, 27(3): 284-288.(in Chinese)

4 CHEN S C, HUANG K J, CHEN W H,et al. Quattroped: a leg-wheel transformable robot [J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(2): 730-742.

5 CHARIOT C,FILIPPI E,VERLINDEN O. CPG tuning using sensory feedback for walking applications[C]∥Proceedings of the ECCOMAS Thematic Conference on Multibody Dynamics, 2013: 721-730.

6 VLADISLAY K. Design, modeling, and characterization of a miniature robotic fish for research and education in biomimetics and bioinspiration[J]. IEEE/ASME Transactions on Mechatronics, 2013, 18(2):471-483.

7 MAHMOUD T, CARLOS V, LINO M, et al. OmniClimbers: Omni-directional magnetic wheeled climbing robots for inspection of ferromagnetic structures [J]. Robotics and Autonomous Systems, 2013, 61(9): 997-1007.

8 SCHROER R T, BOGGESS M J, BACHMANN R J, et al. Comparing cockroach and whegs robot body motions[C]∥IEEE International Conference on Robotics and Automation, 2004,4: 3288-3293.

9 LIUJ J, PASUPAT P, CYPHERS S, et al. Asgard: a portable architecture for multilingual dialogue systems[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing, 2013: 8386-8390.

10 EICH M, GRIMMINGER F, KIRCHNER F. A versatile stair-climbing robot for search and rescue applications[C]∥IEEE International Workshop on Safety, Security and Rescue Robotics, 2008: 35-40.

11 HUANG B, WANGP F, SUN L N. Behavior based control of a hybrid quadruped robot[C]∥6th World Congress on Intelligent Control and Automation, 2006: 8997- 9001.

12 WANG P F, HUANG B, SUN L N. Walking research on multimotion mode quadruped bionic robot based on moving ZMP[C]∥International Conference on Mechatronics & Automation,2005: 1935-1940.

13 罗洋，李奇敏，温皓宇.一种新型轮腿式机器人设计与分析[J].中国机械工程，2013，24(22)：3018-3023. LUO Y,LI Q M,WEN H Y. Design and analysis of a new kind of wheel-legged rover[J]. Chinese Mechanical Engineering, 2013，24(22)：3018-3023.(in Chinese)

14 徐坤，郑羿，丁希仑.六轮腿式机器人结构设计与运动模式分析[J]. 北京航空航天大学学报，2016，42(1):59-71. XU K,ZHENG Y,DING X L. Structure design and motion mode analysis of a six wheel-legged robot[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016，42(1):59-71.(in Chinese)

15 OTTAVIANO E,VOROTNIKOY S,CECCARELLI M,et al. Design improvements and control of a hybrid walking robot [J]. Robotics and Autonomous Systems, 2011, 59(2): 128-141.

16 MARCONI L,LEUTENEGGER S, LYNEN S,et al. Ground and aerial robots as an aid to alpine search and rescue: initial SHERPA outcomes [C]∥2013 IEEE International Symposium on Safety, Security, and Rescue Robotics, 2013:251-256.

17 布鲁诺·西西里安诺,洛伦索·夏维科,路易吉·维拉尼,等.机器人学建模、规划与控制[M].张国良，曾静，陈励华，等译.西安：西安交通大学出版社，2015:177-218.

18 梅莱J P.并联机器人[M].黄远灿，译.北京：机械工业出版社，2014:187-195.

19 冯李航，张为公，龚宗洋，等. Delta 系列并联机器人研究进展与现状[J]. 机器人， 2014，36(3)： 375-384. FENG L H， ZHANG W G， GONG Z Y，et al. Developments of Delta-like parallel manipulators a review[J]. Robot，2014，36(3)： 375-384.(in Chinese)

20 王冰, 聂旭萌, 韩书葵. 一种平面二自由度并联机器人的设计空间及其灵巧性分析[J]. 机械传动, 2015,39(4): 37-40. WANG B, NIE X M, HAN S K. Analysis of the design space and dexterity of a planar two degree of freedom parallel manipulator[J]. Mechanical Drive,2015, 39(4): 37-40.(in Chinese)

21 LI Q, HERYE J M. Type synthesis of 3-DOF RPR-equivalent parallel mechanisms[J]. IEEE Transactions on Robotics, 2014, 30(6): 1333-1343.

22 CHEN X, XIE F, LIU X, et al. A comparison study on motion/force transmissibility of two typical 3-DOF parallel manipulators: The sprint Z3 and A3 tool heads[J]. International Journal of Advanced Robotics Systems, 2014, 11(1): 1-10.

23 廖明，刘安心，沈惠平，等．并联机构方位特征集的符号推导方法[J/OL].农业机械学报，2016，47(3):395-404．http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160356&flag=1.DOI:10.6041/j.issn.1000-1298.2016.03.056. LIAO Ming，LIU Anxin，SHEN Huiping，et al.Symbolic derivation of position and orientation characteristics of parallel mechanism[J/OL].Transactions of the Chinese Society for Agricultural Machinery，2016，47(3):395-404.(in Chinese)

24 朱小蓉，宋月月，孙晨，等. 2RRUR-2RSS并联机构结构特性与运动学分析[J/OL].农业机械学报，2016，47(12):408-415.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20161252&flag=1.DOI:10.6041/j.issn.1000-1298.2016.12.052. ZHU Xiaorong，SONG Yueyue，SUN Chen， et al.Structural characteristics and kinematic analysis for novel 2RRUR-2RSS parallel mechanism[J/OL].Transactions of the Chinese Society for Agricultural Machinery，2016，47(12):408-415.(in Chinese)

Dynamics Investigation of RUPU-RUPR Spherical Parallel Mechanism for Wheel-Legged Mobile Robot

SANG Donghui CHEN Yuan GAO Jun

(SchoolofMechanical,Electrical&InformationEngineering,ShandongUniversity，Weihai264209，China)

A kind of 2-DOF spherical parallel mechanism was presented. Based on the mechanism, a type of wheel-legged mobile robot was developed, which had a simple structure and a good obstacle climbing ability. According to the design theory for parallel mechanisms based on position and orientation characteristic equation and the principle for the coupling degree reducing, a novel 2-DOF spherical parallel mechanism was proposed. The inverse kinematics, workspace, velocity and acceleration model of RUPU-RUPR spherical parallel mechanism were modeled by using analytic geometry method and closed loop constraint equation. The workspace, velocity and acceleration solutions were verified by numerical methods. The dynamic equations of RUPU-RUPR spherical parallel mechanism was also established by Newton-Euler formulation. Given the platform moving rules and external forces, the driving torque of the RUPU joint and the constraints torque of the RUPR joint were calculated. A simulation solution of the dynamic model was given. The results illustrated that the spherical parallel mechanism had a simple mechanical structure and large workspace. The research provided a theoretical base for its kinematics and dynamics and workplaces of this spherical parallel mechanism.

wheel-legged mobile robots; spherical parallel mechanism; dynamic model

10.6041/j.issn.1000-1298.2017.08.045

2017-04-18

2017-06-14

国家自然科学基金项目(51375264)和山东省科技重大专项(2015JMRH0218)

桑董辉(1989—)，男，博士生，主要从事机器人机构学研究，E-mail： sdwhsdh@163.com

陈原(1976—)，男，副教授，主要从事机器人机构学研究，E-mail： cyzghysy@sdu.edu.cn

TP242; TH113

A

1000-1298(2017)08-0376-08