2017年高考数学上海卷数列试题解析——兼谈上海卷的特点

上海市市西中学 庞良绪 (邮编:200040)

复 习考 试

2017年高考数学上海卷数列试题解析
——兼谈上海卷的特点

上海市市西中学 庞良绪 (邮编:200040)

1 高考数学上海卷数列试题评析

数列试题堪称变化最大,一改“往年高考压轴题一般是数列题”这一格局,今年第3道解答题是数列,难度中档,第10题填空题和第15题选择题也是两个难度中档的数列试题,试题不偏不怪,看起来显得亲切自然,似乎和平时的训练题有几分相似之处,体现了“教考一致”的导向作用.不难看出,今年高考对数列的考查变一题(压轴题)把关为多题(填空题、选择题与解答题)把关,分散了难度,降低了门槛,充分考虑到学生的思维层次和能力层次,适合不同思维层次水平的学生,为“文科生”增加了得分的机会,充分考虑到了文理兼顾.在试题的设计上,既注重考查学生的基本知识和基本技能,同时也注重考查数学核心素养、思维能力.数学抽象、数学推理、数学建模也成为试卷的亮点.下面以数列试题为例作一解析:

1.1 注重数学阅读能力,突出数学语言相互转化

考题(10) 已知数列{an}满足:an＝n2,n∈N∗,若对于一切n∈N∗,{bn}中的第an项恒等于中的第项,则_____.

学生读起来显得很“别扭”,不习惯、不够顺口,但这也正是数学语言的魅力所在,是高度抽象性的体现.数学符号是数学抽象思维的产物,是数学交流与传播的媒介,是进行数学推理的工具,因而在教学中应该重视对学生的数学符号语言的阅读、理解、转化、表达、探究、调控能力的培养.

分析 已知an＝n2,由{bn}中的第an项恒等于{an}中的第bn项,即ban＝bn2＝abn＝(bn)2,即ban＝(bn)2,所以,故

1.2 注重基本概念理解,落实数学核心素养的考查

《普通高中数学课程标准》指出:要培养学生的语言概括能力、归纳能力、逻辑推理能力,感悟数学核心素养以及体验数学活动的过程.“充分条件与必要条件”是掌握和使用数学语言的基础,是研究命题条件、结论关系的一个重要概念,同时,对“充要条件”这一概念的理解,可以帮助学生加深对其它数学知识的理解和掌握.

考题(15) 已知数列xn＝an2＋bn＋c,n∈N∗,使得x100＋k,x200＋k,x300＋k成等差数列的必要条件为( )

A.a≥0 B.b≤0 C.c＝0 D.a－2b＋c＝0

分析1 因为x100＋k,x200＋k,x300＋k成等差数列,即2x200＋k＝x100＋k＋x300＋k,即2(a(200＋k)2＋b(200＋k)＋c)＝a(100＋k)2＋b(100＋k)＋c＋a(300＋k)2＋b(300＋k)＋c.

化简可得2a(200＋k)2＝a(100＋k)2＋a (300＋k)2,整理得－2a＝0,即a＝0,故选A.

分析2 函数xn＝an2＋bn＋c中,假若a≠0,则函数是二次函数,而二次函数存在凹凸性,不满足2x200＋k＝x100＋k＋x300＋k,与已知矛盾.即a≠0不成立,所以a＝0满足.故使得x100＋k, x200＋k,x300＋k成等差数列必要条件是a＝0,故选A.

中国数学学会理事长、院士马志明先生说:“……学好本领不是一定要学会很多知识,是一定要学会将来进入社会之后怎样继续学习积累知识,……一个真正有本事的人,真正做出成就的人,他是善于不断学习的,……”阅读理解能力是学习能力的一个重要方面,高考加强阅读理解能力的考查不仅势在必行,更在情理之中.

1.3 注重数学应用能力,提升数学核心素养

考题(19) 共享单车问题:每月供应量

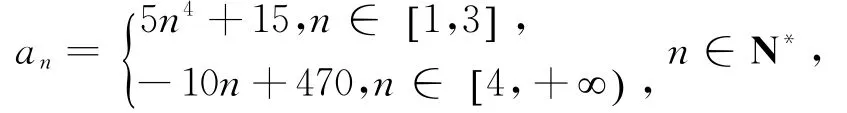
每月损失量bn＝n＋5(n∈N∗),保有量Q为an的累计量减去bn的累计和.

(1)求第4月的保有量;

(2)Sn＝－n－46()2＋8800,记Sn为自行车停放点容纳车辆,当Q取最大值时,停放点是否能容纳?

把数学与共享单车等联系起来,题目背景设计体现时代感,与互联网＋、共享经济等相呼应,既反映社会热点,也体现出数学的应用性,给考生以清新自然的亲切感,让高考不再是“天马行空”.

分析 (1)由a1＝20,a2＝95,a3＝420,a4＝430,b1＝6,b2＝7,b3＝8,b4＝9,

得第4月的保有量Q＝(a1＋a2＋a3＋a4)－(b1＋b2＋b3＋b4)＝935.

(2)当n≥4,n∈N∗,Q＝(a1＋a2＋a3＋a4＋…＋an)－(b1＋b2＋b3＋b4＋…＋bn)＝

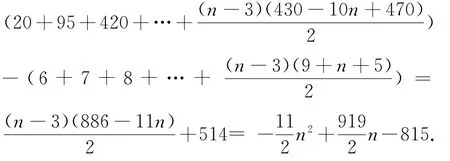
所以,

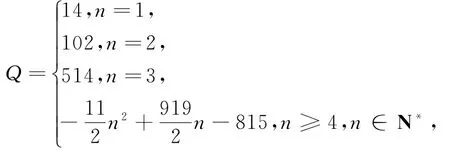
当n＝42时,Q取得最大值8782.

此时,S42＝－(42－46)2＋8800＝8784＞8782,所以当Q取最大值时,停放点能容纳.

2 高考数学上海卷的特点

2017年高考数学上海卷的整体特点是:体现课改方向,平稳中凸显亮点.

2017年是上海市新高考的元年,上海市2017届高考生一直都是在教育改革的“新环境”中度过.作为全国高考改革试点的上海与浙江,由于不分文理科(文理合卷),又作为全国高考改革试点,因此具有风向标和定海神针的示范效应.新课改的首次高考题目刚一面世就引起关注与议论.教师中有人说“眼前一亮”;有人说“有点出乎预料,压轴题居然是抽象函数”;还有人说“试题的设计有梯度”.学生中有人说“乍一看难度不大,细做下来发现有几个小题和证明题拿不准”.一时间,数学试题与评价成为上海市(乃至全国)的一个热门话题.作为高三一线教师,我们再没有比看到数学试题备受关注更欣慰的了,高兴之余也情不自禁地参与到交流中来.直观感觉:2017年上海市高考数学卷在平稳过渡中见新奇,在能力立意中见创新.试题蕴涵着课本中重要的思维方式和思想精髓及数学核心素养.与往年的高考数学试卷相比,在题量、分值上都体现出相应的调整.首先,题量由原来的23题减少为21题,12道填空题,4道选择题,5道解答题(比往年少了2道填空题).其次,填空题分值上的变化,由往年的每题4分调整为1到6题每题4分, 7到12题每题5分,总分由原来的56分减少至54分.

从试卷的结构来看,今年的试卷中函数、数列、解析几何、三角、立体几何等内容仍然是“重头戏”.删去了往年“仅理科生考的极坐标,离散型随机变量的期望、方差”;往年仅理科生考的“和(积)事件的概率和参数方程”,今年对所有考生是必考内容,往年仅文科生考的三视图和线性规划,今年对所有考生都是必考内容.呈现出:容易题以往年的文科生为起点,最难的题以往年能力较强的理科生为终点.试卷整体难度控制较理想,入手比较容易,增加了中档题的题量,但也有相当坡度,难度层层递进,具有良好的区分度.填空题、选择题与解答题的最后一至两题为把关题,均设置了一定难度,符合学生的解题习惯,但解答题以抽象函数压轴又出乎意料.知识与能力并重,“通俗”与“高雅”交融,平凡与创新齐飞,秋水共长天一色.

3 对2018年高考的启示

新高考传递了这样的信息:“做题不在多,理解会用则行;解法不在全,联系变化才灵”.通法为主,变法为辅.重视通性通法,倡导举三反一与举一反三、一题多解和多题一解,努力培养以“五种能力、两个意识”为载体的数学核心素养,要为思维而教.

要还课堂于学生.课堂教学中应注重知识的形成过程的探究,培养学生自主探究的能力,重视知识传授的同时,更要重视数学思想方法的渗透,培养学生提出问题、分析问题、探究问题和解决问题的能力.比如考题(10),不少学生读不懂题目,究其原因:不能实现数学语言的相互转化,即文字语言与符号语言如何转化.因此,在教学中让学生自主读题,让学生独立思考,让学生独立做题,让学生独立运算,就不能吝啬时间.

精讲精练.一道题做透了,要远胜于做一百道题.好的高考题,不一定都是新题,它往往是源于课本,源于平时的训练题,透过今年高考的数列试题,可以看出命题人没有刻意回避教辅资料中常见试题,追根溯源有些是形不似而神似,有些是形似而神不似.因此,教师在课堂上应讲学生的疑点、讲知识的来龙去脉、讲数学方法、讲概念公式形成的“返璞归真”,对于新高考背景下,那些仅会套用公式,按照解题套路解题的学生,或是从题海战术出来的“勇士”们可能会“牺牲”出局.

教育家杜威曾说:“教学绝对不仅仅是简单地告诉,教学应该是一种过程的经历,一种体验,一种感悟”.教师应向学生展示数学的本质,关注数学思想方法的回归,多讲几个为什么?追求数学感悟、真懂,使学生的学习过程成为教师引导下的释疑解惑、质疑问难的思维过程,培养数学核心素养的再创造过程.

要关注探究、变式、拓展、创新题,尽量少用几十年不变的陈题,及时归纳解题的思维方法,激发头脑的思维风暴;关注题型的多向发展,重视纵横联系;拓展母题的思想方法,加强多元交汇,使对知识与思想方法的掌握达到“鹰击长空,鱼翔浅底”的境界.

2017-06-29)