横看成岭侧成峰 远近高低各不同——以一道题目为例谈探索式论证与一题多解

安徽省合肥市第一中学 范可欣 任孝辉 (邮编:230601)

横看成岭侧成峰 远近高低各不同
——以一道题目为例谈探索式论证与一题多解

安徽省合肥市第一中学 范可欣 任孝辉 (邮编:230601)

数学是一门研究数量关系和空间形式的科学.数学研究的过程应该是我们从感性认识到理性认识的过程.正如“横看成岭侧成峰,远近高低各不同”所描述的那样,从不同的视角出发,会看到同一研究对象的不同现象面.

对于中学生而言,数学解题是我们经常从事的数学活动.我们必须从数学研究意识的高度来从事这一活动,才能经历从感性认识到理性认识的过程,体会到数学知识的联系与发展,提高数学问题解决的能力,提升我们的创新意识与应用意识.“一题多解”就是我们实现这一目的的有效途径.

“一题多解”的过程,应该是解题者“运筹”的过程,即根据客观现实制定切实可行、行之有效的解题计划与方案,从而实现“运筹帷幄于一题之中,顺利决胜于千题之外”.波利亚在《怎样解题》和《数学的发现》中早就给出了“运筹策略”,那就是“怎样解题表”和“探索式论证”策略.现以一题为例,分享探索式论证与享受的过程.

1 探索式论证的过程与表示

波利亚指出,探索式论证的目的是发现当前问题的解,过程是依据题目的已知条件,通过满足于一个或多个看似可信的猜测,得到当前问题的求解思路.为了将探索式论证的思维过程直观化,波利亚还给出了解题过程的几何图示方法.

1.1 题意的理解与几何图示

“题意的理解(理解题目)”是波利亚“怎样解题表”的第一步,分为熟悉题目和深入理解题目两个阶段[1].首先,我们应该在理解题目语言陈述的基础上,确定题目的主要部分,即未知量、已知数据及条件;其次,将已知条件和未知量(求解目标)几何表示.

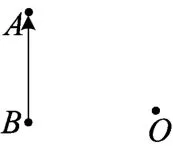
图1

1.2 思路的探索、图示与实现

波利亚认为,为了提高猜测的可信度,在思路的探索过程中要注意两点.一是紧盯求解目标不放,二是深挖求解目标和已知条件的数学背景[2].这些工作是必须的.它不但可以一直保证思路探索方向的正确性,还能为一题多解提供丰厚的土壤,从而多角度地寻求已知条件和求解目标的联系,构建尽可能多的思维路径.

对于本题而言,求解目标为:a2＋b2＝1.常规而言,该目标的背景有两个.一个是表示a、b关系的方程,第二个是平面上圆心为原点,半径为1的圆.在图1基础上,就可以将求解目标具体化,将点O根据不同视角(背景)进行分解,分别为点O

1,O2(图2).

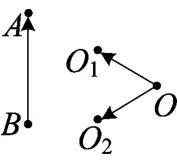
图2

思路1 (寻求从A到O1的思路):条件A和B表示的是实数a、b之间的关系,求解目标也是实数a、b之间的关系.从A点应该怎样继续前进呢?一个常规的想法就是对条件A进行变形,重要的节点是化无理为有理,表示为点C,则图2可进一步改进为图3(虚线表示该思路只是一个探索性的猜想).

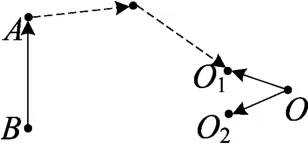
图3

波利亚特别强调,探索式论证只是暂时的和看似合理的,并不能作为最终严格的论证,二者不可以混淆.所以,接下来,我们就要沿着思路1进行严密论证.

两边平方得,a2(1－b2)＝1＋b2(1－a2)(1,整理得(1－a2)＝0.

上述证明过程表明,思路1是可行的,图3中有向线段AC和CO1就可以改为实线段了.

2 解题思路的回顾与反思:其他思路介绍

思路的探索、图示和实现的过程相当于波利亚“怎样解题表”中的第二步和第三步,即拟定方案和执行方案的过程.通常,我们一般都会终止解题活动,因为答案已经出来了,求解目标已经实现了.但是,波利亚特别指出,如果这样做,你会遗漏了解题中的一个重要而且有益的阶段——回顾与反思.在这一阶段,我们可以进一步巩固知识,将解题方法加以改进,深化我们对答案的理解.

一般地,在回顾与反思阶段,我们需要问自己3个问题:你能检验这个论证(结果)吗?你能以不同的方式推得这个结果吗?这个题目能进行推广吗?现仅以第2个问题为例来说明反思过程.

思路2 (寻求从A到O2的思路)

求解目标O2表示平面上圆心为原点,半径为1的圆,即让我们证明满足条件A和B的点(a,b)都在该圆上.条件A表示点(a,b)满足a.显然,若＝a,,结论显然成立.于是可将点O2向前推进到点D:＝b.将条件A和条件D进一步比较,就可以发现三角换元,将之表示为条件E.至此,思路2形成(图4).

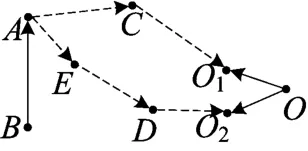
图4

故a2＋b2＝1.

可见,思路2也是可行的,那么图4中有向线段AE、ED和DO2也可以改为实线段了.

当然,如果我们头脑中存储与已知条件、求解目标关联的知识多、解题经验丰富,还可以看到柯西不等式、向量、单位圆切线、点线距、基本不等式和函数等背景.这些探索式论证思路的形成与表示与思路1和思路2是相同的,在此不多赘述,只简要叙述思路.

按照波利亚的“怎样解题表”和“探索式论证方法”可以实现有序思考,从尽可能高的深度和广度来认识每一道题,领悟解题过程中的数学思想方法,不断提高数学解题能力.波利亚认为“没有任何一个题目是可以彻底完成了的”.因此,只有对每一道题目一题多解,找出联系,进行推广,才能避免“不识庐山真面目,只缘身在此山中”.

1 [美]G波利亚.涂泓,冯承天译.怎样解题—数学思维的新方法[M].上海:上海科技教育出版社,2011

2 [美]G波利亚.刘景麟,曹之江,邹清莲译.数学的发现—对解题的理解、研究和讲授[M].北京:科学出版社,2013

2017-06-12)