去伪存真 再谈《弧度制》教学

华中师范大学数学与统计学学院 王 乐 熊惠民 (邮编:430079)

去伪存真 再谈《弧度制》教学

华中师范大学数学与统计学学院 王 乐 熊惠民 (邮编:430079)

弧度制,一直以来都被认为是高中数学的一个教学难点.其主要原因是对弧度制引入的必要性缺乏正确的理解.不少人认为弧度制的引入使得角的集合与实数集合建立一一对应的关系,从而将三角函数可以定义在实数集上.事实上,无论是弧度制还是角度制,都能在角的集合与实数集合之间建立一一对应的关系(例如30°30′的角对应实数30.5);也有人认为角度制是60进位制,弧度制是10进位制,我们一般用的都是10进制,所以要学弧度制.进制是人们规定的一种进位方法,对于任何一种n进制,就表示某一位置上的数运算时是逢n进一位,对于角度制有1度等于60分,1分等于60秒,可以说它是60进位制,但弧度制只有弧度这一种单位,说它是10进位制是欠妥的.实际上,弧度制与角度制都是度量角的单位制,本质上两者是一样的.正如度量长度不仅有米、千米还有厘米、毫米甚至尺、公里等不同单位制;度量重量不仅有克、千克也有斤、公斤、吨、磅等.但是,在微积分创立之后弧度制的引入使得三角函数的微分公式、积分公式、泰勒公式等相比于普通角度制得到了极大的简化[1],这使得弧度制成为了高等数学的一个必然选择,这也是弧度制引入的真正意义.然而对于高中生而言,弧度制的学习所带来的便利又是显而易见的.因此,明确弧度制引入的意义,理清角度制与弧度制的转化关系,掌握弧度制下弧长与扇形面积的计算公式是本节课的重中之重.下面提供一个课例以期与读者共同探讨,在中学数学中怎样教弧度制.

1 教学实录

1.1 提出问题

师:同学们,前面我们学习了哪些度量长度的单位?

生:学习了千米、米、厘米、毫米、里、公里……

师:那我们还学习了哪些度量重量的单位呢?

生:有千克、克、吨、斤、公斤……

师:很好!我们看到度量长度或重量有很多种单位,那么不同的度量单位之间有关系吗?

生:有关系.它们之间可以互相换算.例如,1千米＝1000米＝1公里;1吨＝1000千克.

师:说的很不错!正是因为这样,在生活中我们会选择不同的单位来度量同一事物.

1.2 探究新知

师:对于一个角,我们学过哪些度量单位呢?

生1:度(°)、分(′)、秒(″).

师:你还记得我们是如何用“度”来度量角的吗?

生1:把一个周角规定为360度,它的1/360为1度的角,记做1°,1°＝60′,1′＝60″.

师:说的很好!初中时候我们把用“度、分、秒”作为单位来度量角的制度叫做角度制.同样的,角的度量也有不同的单位制.今天我们就来学习一种新的度量角的单位制——弧度制,即把一个周角规定为2π弧度(记作2πrad),把用“弧度”作为单位来度量角的制度叫做弧度制.

师:请大家思考一下,角度制和弧度制之间有什么区别呢?

生:角度制是把一个周角规定为360°,弧度制是把一个周角规定为2πrad.

师:很好,这就是它们的差别,也就是说360°可以用2πrad来表示,那么平角等于180°等于多少rad呢?

生2:180°＝πrad.

师:不错,是πrad,那你是怎么得到的呢?

生2:因为周角就是平角的两倍,而周角是2πrad,所以180°＝πrad.

师:你们都同意他的看法吗?

生3:我觉得角度制下周角是平角的两倍,弧度制下不一定吧.

生4:角度换成弧度只是单位的换算,周角和平角之间的倍数关系应该是不变的.

师:生3能发现问题很不错.实际上这是由于角的可加性,两个平角构成一个周角.单位制的不同并不改变角的可加性,因此180°＝πrad是正确的.

生:根据上面的分析,两个直角构成一个平角,所以90°＝πrad.

2

师:完全正确.可以看到“度”与“弧度”可以进行换算.但这些角都是特殊角,你会计算1°＝rad吗?你是怎么算的呢?

生5:因为周角是360°＝2πrad,左右两边同时除以360就得到rad,将右边化简就得到rad.

师:非常好!我现在给你一个任意度的角,你知道它是多少弧度吗?即若一个角为n°, αrad,那么n与α之间有什么样的关系呢?

师:很好!根据上述公式,我们就可以对任意角进行弧度与角度的换算.大家要注意,今后用弧度制表示角时,“弧度”二字或者“rad”通常略去不写,只写该角对应的弧度数.

例1 将下列角度制与弧度制互化:(略)

(1)75° (2)60°30′ (3)480°

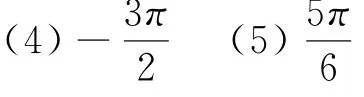
例2 计算下列各式的值:(略)

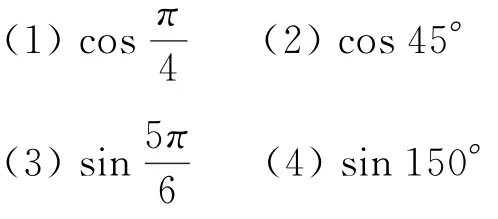
1.3 拓展创新

师:初中的时候我们学习了弧长公式和扇形的面积公式,大家还记得吗?

生:半径为r,圆心角为n°的弧长公式和扇形的面积公式分别是:

师:这是建立在角度制上的公式,现在你学习了弧度制,你能用弧度表示它们吗?你准备怎么做?

生8:上面的公式是角度制公式,现在要转换成弧度制公式,只需要将角度n用弧度来表示就可以.

师:很好.这里的n表示的是角度,现在我们假设n°＝αrad,那公式变成什么了呢?

师:说的很好!大家还有其它想法吗?

生10:不用换算也可以,弧度制中的周角是2πrad.αrad的角占了周角的那么它所对的弧长就是,其扇形的面积就是

师:很好!学以致用,学了弧度制就要用它,这样不是更简单嘛.

师:之前我们将角推广到了任意角,我们知道角有正角、负角和零角,通过角度与弧度的互化,我们也看到了弧度数也有正负之分,但是弧长与扇形面积都是非负的,那我们是不是需要把原来的公式稍加改动呢?

师:很好,这样我们算弧长和扇形面积就不会受到正负角的影响了.

生11:说明弧度α就是弧长l和半径r之比.师:能不能说的更通俗一点呢?

生12:说明弧长l等于半径r的α倍.

师:很好!也就是说弧长l等于α个半径r.由此我们可以看出弧度α就是用半径r来度量弧长l.例如,弧长l等于2个半径r,就说弧度数为2,即这个角为2rad.那么α＝1说明什么呢?有什么意义呢?

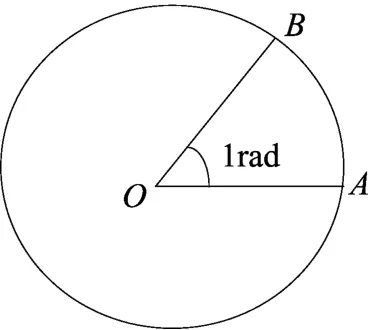
生13:弧度数α＝1,即弧长等于一个半径,也就是说此时弧长等于半径.

师:很好!也就是说1 rad的角就是长度等于半径长的弧所对的圆心角.如图,圆O的半径是r,弧AB的长等于半径r,那么∠AOB就是1rad的角,这就是1rad的意义.

下面请大家看这道例题:

例3 分别用角度制、弧度制下的弧长公式计算半径为1m的圆中,60°的圆心角所对的弧的长度.(略)

师:到这里,本节课的主要内容已经说完了.请大家思考一下,已经有了角度制为什么还需要弧度制呢?

生14:弧度制不用写单位,更加简单.

生15:采用弧度制,弧长公式和扇形面积公式简单多了,计算起来很方便.

师:说得很好,这也正是引入弧度制的原因之一.当然,弧度制的引入还有更大的作用,在以后学习高等数学的时候大家就清楚了.

1.4 课堂小结

师:通过本节课的学习你有哪些收获、体会和问题?

学生积极参与讨论,主要观点如下:

(1)我知道了一种新的度量角的制度——弧度制,它和角度制都是度量角的单位制.

(2)我知道了角度制是把一个周角规定为360°,弧度制是把一个周角规定为2πrad.

(5)我还知道了1rad的意义(1rad的角就是长度等于半径长的弧所对的圆心角).

师:大家总结的都很好,这节课要掌握的主要内容有三个:一是学习一种新的角的度量制度,即弧度制;二是会把任意角的角度与弧度进行互化;三是掌握弧度制下弧长与扇形面积的公式.至于弧度制在高等数学中究竟有哪些好处,大家课下可以查阅资料了解一下.

1.5 布置作业

书面作业(A类、B类):略.

思考题:略.

2 课例解析[2]

弧度制引入的主要原因是为了适应微积分创立后科学计算上的需要,这是高等数学中的问题.而在中学数学中,学生更多的是要体验弧度制带来的便利.正是对弧度制引入的理解偏差,大部分教师将弧度的概念定位为本节课的难点,花大部分的时间苦苦寻求1弧度的定义,忽视了对于高中生而言弧度制学习的意义,使得一个不被学生认为是难点的知识反而成为了教师公认的难点,弧度制成了“糊涂制”.

与教材的做法和一般教学设计不同,课例不是先学习1弧度的角后再定义弧度,而是先让学生体会不同单位制的好处,顺势在复习角度制后直接提出弧度制的定义,有了弧度制的定义,学生自然会比较这两种定义.从而过渡到探究弧度与角度的关系,然后再让学生运用弧度制,得到弧度制下的两个新的计算弧长公式和扇形面积公式,最后再借助已得到的弧长公式说明了1弧度的意义.整个过程是建立在学生的“最近发展区”,学生的思考是按照需要解决的问题一步步进行的,这对于学生而言是容易接受的.另外,需要学生掌握的知识也很自然的生成,教师只是穿针引线者.从学生对于本节课的收获中可以看到,学生抓住了本节课的重点(一种新的角的度量制度即弧度制;角度与弧度进行互化;弧度制下弧长与扇形面积的公式),并没有受一些细枝末节知识的干扰,这也恰好说明了教学设计的成功.当然,教无定法,在实际授课当中难免遇到意想不到的情况,这也需要教师能够居高临下,在具体实施的时候,合理把控.

1 李忠.为什么要使用弧度制[J].数学通报,2009,48 (11):1-4

2 熊惠民.平面向量基本定理的教学设计[J].数学通讯, 2012(7):15-18

2017-05-13)