基于GRA-GSBP选矿成本预测的研究

杨 刚，王建民

（华北理工大学 电气工程学院，河北 唐山 063009）

基于GRA-GSBP选矿成本预测的研究

杨 刚，王建民

（华北理工大学 电气工程学院，河北 唐山 063009）

针对选矿成本影响因素较多，各因素间存在耦合和非线性关系以及BP神经网络隐含层节点数难以选择的问题，提出一种基于灰色关联分析与黄金分割法改进BP神经网络的成本预测法。首先运用灰色关联分析法计算各因素与选矿成本的关联度，选取关联度最大的四个变量作为BP网络的输入；其次采用黄金分割法搜索历史数据区间中的理想数值，在高精度的要求下，对隐含层节点数频繁出现的区间进行拓展，求得非线性映射能力更强的隐含层网络节点数；最后利用仪表柜中储存的现场数据对成本预测模型进行验证，验证结果证明该方法能够实时准确地预测选矿成本的变化趋势。

灰色关联分析（GRA）；黄金分割法（GS）；BP神经网络；成本预测；关联度；隐含层网络节点数

0 引言

在过去的成本管理中，事后的成本分析具有滞后性，不再适应企业的发展规划。事前的成本预测则更能帮助企业经营者预先制定决策方案，有效地避免企业的损失。由于生产成本高昂，合理准确地预测选矿成本对企业具有重大的意义，随着经济的发展，企业愈来愈重视选矿成本的管理工作，预测成本显得尤为重要。

近年来，随着学者们对智能算法的研究，越来越多的智能算法被应用在成本预测领域，如多元线性回归[1]，指数平滑法[2]，BP神经网络[3]等。由于选矿成本的构成复杂，各因素之间错综复杂，相互影响，具有非线性、大惯性等特点，因此，很难找到一个精确的数学模型来描述影响因素与成本之间的关系。而BP神经网络是包含输入层、隐含层、输出层的多层前馈网络，是基于误差逆传播算法进行训练的智能算法，不依赖于数学模型，能够实现非线性映射，并且具有广泛的适应性，避免了复杂的数学运算，目前，许多学者将其应用在成本预测领域。目前已成功应用于油气钻井[3]、建筑工程[4]、铁路物流[5]等领域。而梁斌等[6]采用模糊巨类法改进神经网络对影响精矿成本的因素进行了分析，确定了各因素对精矿成本的影响度，没有对选矿成本直接预测。郑毅等[7]采用多元线性回归方法所得到的线性关系表达式仅能用于预测呈线性关系的数据，由于选矿成本影响因素间的强耦合性与非线性关系，其预测精度较低。因此，对选矿领域进行成本预测的研究具有很重要的意义，本文采用灰色关联分析法来确定成本的影响因素，运用黄金分割优选法求得最佳隐层节点数，建立了BP神经网络选矿成本预测模型，避免了复杂的数学运算，并将试验结果同基本BP神经网络模型相比较。

1 选矿工艺及成本构成

1.1 选矿工艺基本流程

选矿工艺基本流程包括原矿处理、磨矿、粗选与精选、精矿生产和尾矿处理五个工艺过程（图1）。原矿经过粗碎、中碎、细碎处理后进行筛分为0～13mm的粉矿。粉矿由传送带送入磨机进行磨矿处理。随后进入分级机进行分级，返砂返回磨机重新处理，矿浆经过一道粗选程序和两道精选程序后进行浓缩以及过滤得到铁精矿和尾矿，其中粗选后的废石进行两次扫选处理。

图1 选矿工艺基本流程Fig.1 Technologicalprocessofm ineralseparation

1.2 选矿成本构成

本文以承德兴隆矿业公司为例，该公司位于河北省承德市鹰手营子矿区境内，50多年来累计生产煤炭近6 000万t，最高年产量达到234.7万t，简要分析选矿成本通常由以下几部分组成。

原矿成本；生产用水，电；辅助材料消耗：钢球，皮带，油脂，滤布，药剂，衬板等；动力：煤气，煤；工人工资及差旅费用；设备折旧；修理车间经费。

一方面，选矿成本随着入矿品位和磨矿过程中的参数（比如料球比）的变化而变化；一方面，伴随着入矿量的改变，选矿企业每日的选矿成本也在不断改变，而影响着入矿量的关键参数就是磨机的台时处理量。选矿物料之间的关系式见式（1）～式（3）：

矿粉的瞬时产量为：式中：Pr为入矿品位，%；Pt为精矿品位，%；Pw为尾矿品位，%；Qt为矿粉产量，%；Qr为磨机入矿产量，%。

瞬时耗电量为：

式中：I为磨机电流，A；U为电压，V；cosα为功率因数。

吨产电耗为：

2 灰色关联分析法确定网络输入变量

由于选矿过程具有非线性、大惯性、纯滞后等特点，影响精矿成本的因素很多，比如：入矿品位、精矿品位、台时处理量、尾矿品位、水电单耗等。在预测选矿成本之前，本文采用灰色关联分析法选取与选矿成本关联度较大的因素用于预测[8]。

具体步骤如下：

第一步：变量的无量纲化。

由于影响选矿成本的因素较多且单位不一，在比较之前需要对自变量去量纲化，以便用于分析每个因素的灰色关联度。

式中：Xi（k）表示第i个序列第k个值；Xi（1）表示第i个序列第1个值；xi（k）表示去量纲化后的值。

第二步：计算关联系数。

λ∈（0，∞），λ称为分辨系数。λ越小，分辨力越强。当λ≤0.546 3，分辨力最好。本文取λ=0.5[9]。

第三步：求灰色关联度。

关联系数是反映比较数列与参考数列的关联程度值，关联系数个数等于样本数量，然而过于离散的信息不利于用于整体性的对比[10]。计算公式为：

式中：ri为关联度。

3 黄金分割优选法求隐层节点数

BP神经网络如何选取隐层节点数是其用于实践的一大难题。黄金分割法能够以低成本、试验次数少的优点解决单一的变量求极值的问题，并能快速地搜寻到解决问题的最佳方案，这种先进的优选法已经广泛地应用于生产实践[11]。本文即采用黄金分割优选法搜索最佳神经网络隐层节点数（图2），该方法简便快捷，能够迅速搜索到逼近能力更强的隐层节点数。

设BP神经网络的输入层、隐含层和输出层的节点数分别为pi、pj和po。在实践中，我们发现最佳的隐含层节点数在以下区间出现的概率最大：

然后再根据计算出的样本集的总误差来寻优。设神经网络的总误差为：

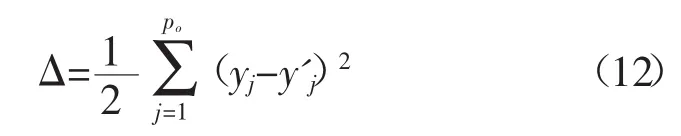
黄金分割优选法步骤如下：

第一步：根据式（11）确定搜索区间[m，n]；

第二步：在第一个测试点x1=0.618×（m-n）+n处进行试验，记录总误差y1；在第一个测试点的对称点x2=0.382×（m-n）+n处进行第二次试验，记录总误差y2；

第三步：比较两次结果，保留有用的部分，如果x1测试结果y1为优，就舍去[m，x2），保留[x2，n）；如果x2测试结果y2为优，就舍去[x1，n），保留[m，x1）；如果x1，x2测试结果一样，就舍去[m，x2）和[x1，n），保留[x2，x1）；

第四步：在保留的区间内重复第一至第三步，直到结果满足要求为止，记此时隐层节点数为P1；

第五步：根据黄金分割原理拓展搜寻区间（[n，h]），其中n=0.618×（h-m）+m，在[n，h]中重复第二至第四步，记隐层节点数为P2；

第六步：将两次搜索得到的隐层节点数代入BP神经网络进行比较，根据实际要求选择逼近能力和泛化能力最适合的节点。

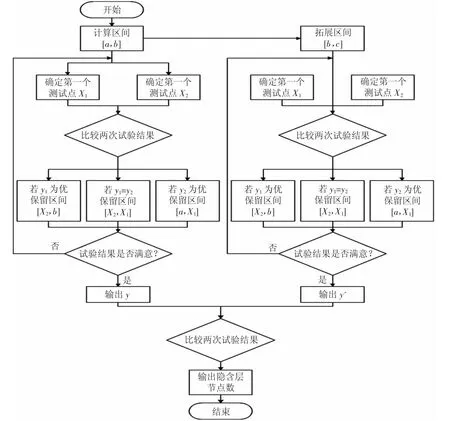
图2 黄金分割优选法流程图Fig.2 Flow chart for Golden Segmentation Optim ization M ethod

4 基于BP神经网络建立成本预测模型

4.1 BP神经网络的原理

1989年，RobertHecht-Nielsen证明一个由输入层、隐含层、输出层三层构成的BP神经网络可以实现任意n维到m维的映射[12-14]，如图3所示。

图3 BP神经网络结构Fig.3 BP neuralnetwork structure

4.2 成本预测模型的建立

本文建立的神经网络预测模型包含三层，即输入层、隐含层、输出层。其中，输入层输入变量有4个，输出层输出变量有1个。

预测模型建立步骤：

第一步：选取100组选矿成本数据作为样本数据，根据式（13）对样本数据进行归一化处理，预处理后的部分数据如表1。

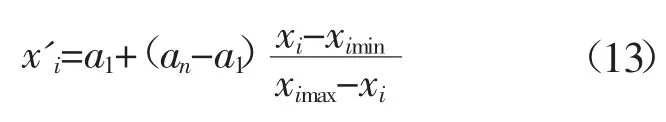
其中：xi为处理前的数据，x'i为处理后映射到区间[0，1]的数据，ximax为第i个影响因素的最大值，ximin为第i个影响因素的最小值，a1、an为转换参数，取a1=0.2，an=0.8。

第二步：采用灰色关联分析法分析各因素与选矿成本的关联度。

选取X0为参考序列，首先计算比较序列与参考序列绝对差Δi（k）值，得到矩阵Δ：

根据式（10）计算出各因素关联度依次为：r01= 0.737 8，r02=0.851 2，r03=0.666 7，r04=0.688 9，r05=0.458 9，r06=0.447 6。选取四个关联度最大的因素分别为：入矿品位、精矿品位、尾矿品位、台时处理量。

根据不完全统计，1979年—2018年，全世界有近200颗顶级蓝宝石被拍卖，其中121颗为克什米尔蓝宝石，拍卖价格高达3.9万—13.5万美元每克拉。在2015年香港苏富比的拍卖会上，诞生了一个每克拉蓝宝石的世界拍卖纪录价，一枚独特的铂金克什米尔镶钻蓝宝石戒指拍出了约670万美元，达到每克拉24.2万美元。

训练BP神经网络，建立反映输入与输出关系的模型。

运用黄金分割优选法求得最佳隐层节点数。

本文采用4-q-1网络结构（图4）建立成本预测模型，模型如图5。

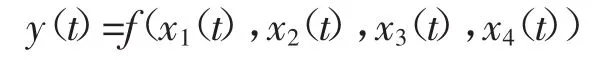
其中：y（t）表示选矿成本，元/t；x1（t）表示入矿品位，%；x2（t）表示精矿品位；%，x3（t）表示尾矿品位，%；x4（t）表示台时处理量，t/h。

图4 4-q-1网络结构Fig.4 4-q-1 network structure

图5 预测模型流程Fig.5 Flow chartof predictionm odel

5 试验结果与分析

5.1 试验平台

仪表柜中存储的数据源来自现场仪表采集的样本数据，通过RS485接口使用Modbus协议将仪表柜与监控计算机（图6）进行通讯，再将监控计算机获取的数据通过SQLSever数据库上传到数据库中，远程计算机通过访问数据库远程获取数据，实时显示运行工况，并将数据打印报表，用于分析挖掘。

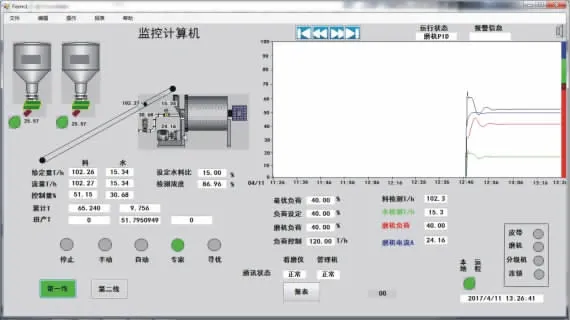
图6 C#监控计算机界面Fig.6 Interface for C#m onitoring computer

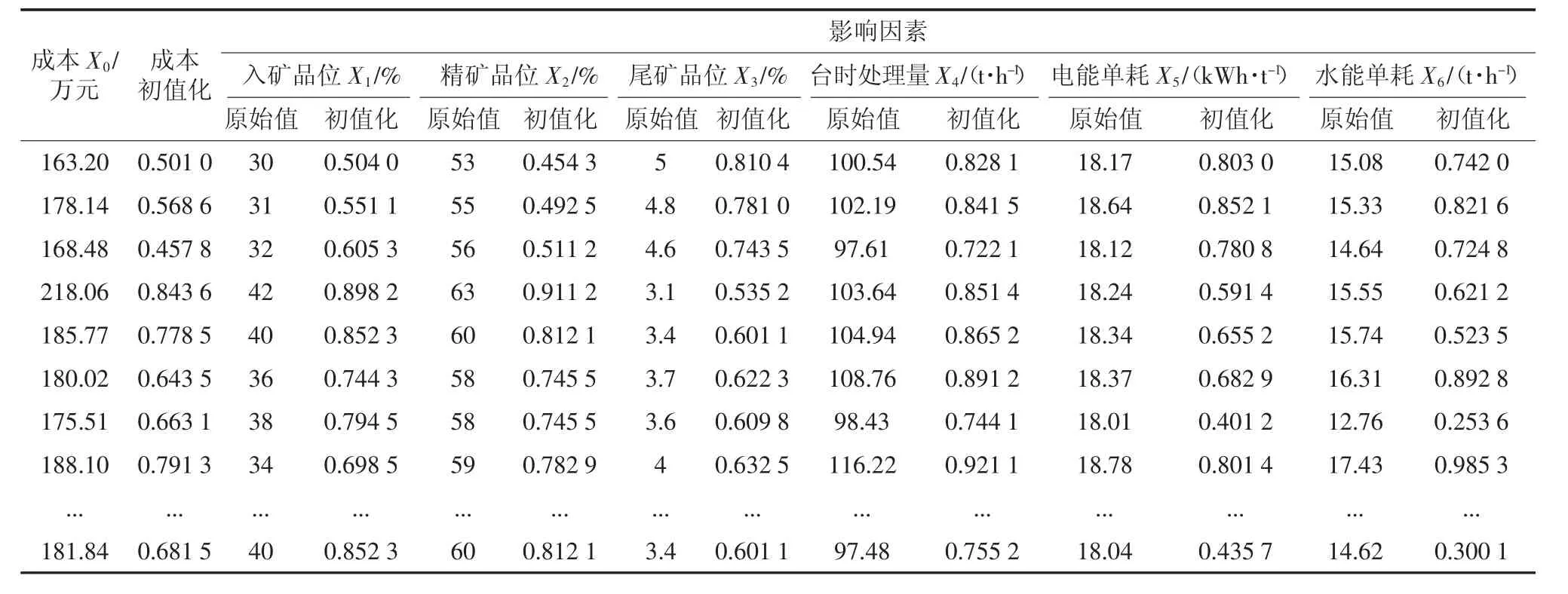
表1 样本数据初值化Tab.1 Initialization of sample data

图6监控计算机的系统操作分为手动、自动、专家和寻优四个模式。图中料、水给定量分别表示表示原矿、水的给定量，料、水流量为现场实时采集的检测量。通过对料、水控制量来调节磨机负荷，从而实现磨机稳定、高效的运行。

（1）手动模式：料水给定量与控制量由操作员根据经验手动输入。

（2）自动模式：给料量由操作员经验人为输入，给水量根据水料比求得，料控制量和水控制量由料PID和水PID自行调节。

（3）专家模式：根据专家经验，欠磨时增加给料量，饱磨时减少给料量。专家控制在料PID与水PID的基础上通过设置重饱磨，中饱磨，轻饱磨，轻欠磨，中欠磨，重欠磨和最优值来实现对执行层的控制。

（4）优化控制方式：优化控制方式就是通过专家经验，设定一个最优负荷值，利用自寻优方式在这个设定值附近寻找出最佳负荷，并根据该最佳负荷控制磨机的给料量。

5.2 参数设置

5.2.1 BP神经网络参数设置

BP神经网络的激励函数取S型函数，学习算法采用高斯—牛顿法（Levenberg-Marquardt算法），因该算法收敛速度最快。在训练神经网络时，只有当网络输出的误差减少为10-4时才停止训练，网络的训练次数为1 000，学习效率设为0.1。

5.2.2 优选法求最佳隐层节点数

采用4-q-1网络结构，则pi=4，p0=1。由式（11）求得m=2，n=15。根据前文所述，首先，在区间[2，15]上确定第一个试验位置x1=0.618×（15-2）+2=10，记录隐层节点数为10时的总误差y1=0.0000525。确定第二个试验位置x2=0.382×（15-2）+2=7，记录总误差y2= 0.000 041 5。试验结果y2为优，因此，去掉区间[10，15），保留区间[2，10）。重复试验，最后得到q1=9时为最佳节点。

其次，根据式n=0.618×（h-m）+m反求得h=23，在拓展区间[15，23]采用优选法，重复试验，求得最佳节点数q2=16。

最后，对4-q-1和4-16-1的BP网络结构分别试验，求得总误差y1=0.000 036，y2=0.000 009 8，测试结果y2为优，因此，选取q=16。

5.3 试验结果分析

BP神经网络学习结束后，采用测试样本建立模型，再将输出结果经过反归一化得到选矿成本预测值。分别采用基本BP神经网络预测模型与改进BP预测模型进行预测，预测结果如图7所示，预测误差曲线见图8，部分预测结果对比如表2。

图7 预测结果Fig.7 Prediction results

由图7可知改进BP预测模型比BP预测模型能够更好地跟踪上实际值，且曲线较为吻合，误差较小。而且图8中的误差曲线也很好地验证了模型的预测精度。此外，由表2中的预测结果对比可知，改进后的BP网络的相对误差更小。因此可得结论，改进后BP模型具有更高的精度。

图9 误差曲线Fig.9 Error curve

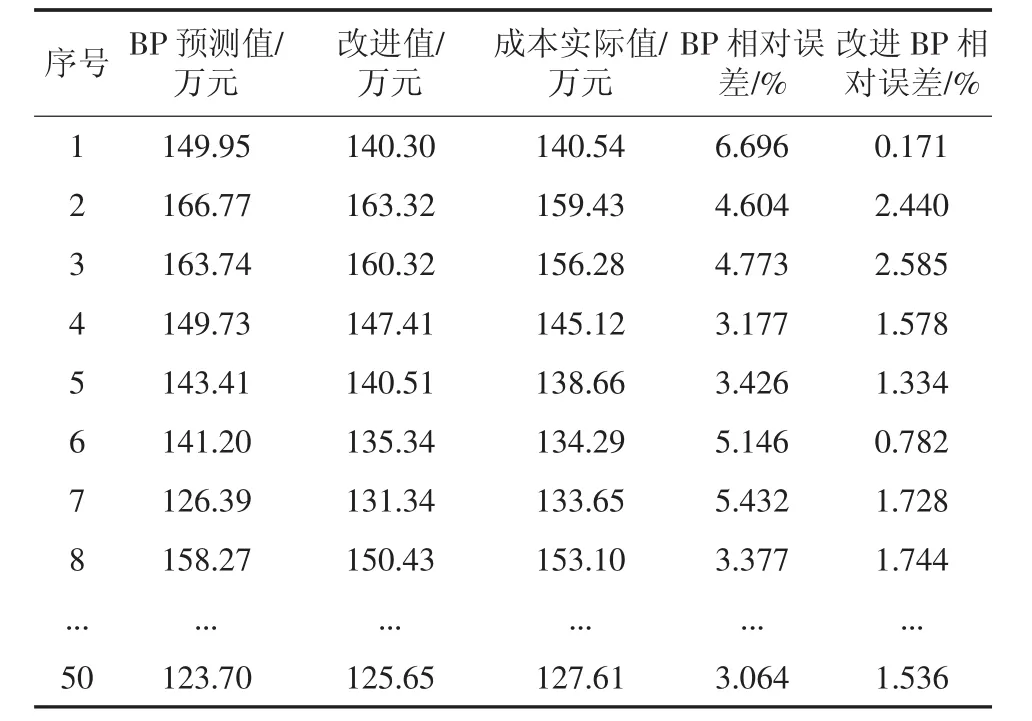
表2 预测结果对照Tab.2 Com parison of prediction results

选取平均百分比误差及训练时间作为成本预测模型的评价指标，结果如表3。

表3 预测模型性能指标对比Tab.3 Com parison of performance indexes

由表可知：（1）BP模型的平均百分比误差为4.86%，而改进后的BP模型的平均百分比误差为1.45%，这对于选矿成本的预测是一个较精确的误差范围，因此文中建立的成本预测模型在预测选矿成本时具有可行性。

（2）虽然两种预测模型的训练时间都不长，但是改进后的BP模型训练时间较短，收敛速度较快，因此，改进后的BP模型能够更快速准确地预测选矿成本。

6 结语

本文提出了一种基于灰色关联分析法及黄金分割法改进BP神经网络的成本预测模型。运用黄金分割优选法得到的最佳隐含层节点数能够有效地帮助BP神经网络训练出准确预测的网络模型，该模型在承德兴隆矿业公司运行良好，能够精确地预测精矿成本的变动趋势，并且，无须建立精确的数学模型，避免了复杂的数学运算，方法简单可行，有助于减少决策的盲目性，降低企业的损失，对类似矿山的选矿成本预测也具有借鉴作用。

[1] 孙淑生，罗宝花.多元线性回归模型在物流成本预测中的应用[J].商业时代，2014（18）：19-21. SUN Shusheng，LUO Baohua.Application of multiple linear regressionmodel in logistics cost forecasting[J].Commercial Age，2014（18）：19-21.

[2] 蓝荣梅.基于指数平滑法的建设项目成本预测研究[D].成都：西华大学，2013. LAN Rongmei.Predictin based on the exponential smoothing building projectcost[D].Chengdu：Xihua University，2013.

[3] 刘天时，赵 越，马 刚.基于BP神经网络的油气钻井成本预测[J].西安石油大学学报（自然科学版），2010（1）：87-90. LIU Tianshi，ZHAOYue，MAGang.Prediction ofoiland gas drilling cost based on BP neural network [J].Journal of Xi'an Shiyou University（Natural Science Edition），2010（1）：87-90.

[4] 金冠航.基于BIM和BP神经网络的成本预测方法研究 [J].建设科技，2017（3）：27-29. JINGuanhang.Research on cost forecastingmethod based on BIM and BP neural network[J].Construction Science and Technology，2017（3）：27-29.

[5] 孙祖妮.基于成本动因BP神经网络的铁路物流货运成本预测[D].北京：北京交通大学，2012. SUN Zuni.The prediction of railway freightcostbased on costdriver and BP neural network[D].Beijing：Beijing Jiaotong University，2012.

[6] 梁 斌，刘 威.铁矿选矿生产过程动态成本控制技术[J].控制工程，2005（6）：66-68. LIANG Bin，LIUWei.On dynamic cost control technology of oredressing production process[J].Control EngineeringofChina，2005（6）：66-68.

[7] 郑 毅，雷围婷.选矿企业成本预测研究[J].科技和产业，2008（8）：34-38. ZHENG Yi，LEI Weiting.The research on cost forecast of beneficiation plant[J].Science Technology and Industry，2008（8）：34-38.

[8] 梅占峰.灰色关联分析法在选矿生产管理中的应用 [J].湖南有色金属，2006（3）：14-15，60. MEI Zhanfeng.Application of grey associate analytical in the managementof dressing poduction[J].HuNan NonferrousMetals，2006（3）：14-15，60.

[9] 赵加凡，陈小宏，张 勤.灰色关联分析在储层评价中的应用[J].勘探地球物理进展，2003，26（4）：282-286. ZHAO Jiafan，CHEN Xiaohong，ZHANG Qin.Application of grey association analysis in reservoir evaluation [J].Progress in Exploration Geophysics，2003，26（4）：282-286.

[10]黄速建，李 倩，王 季.我国不同所有制工业企业效率比较评价——基于熵权法和灰色关联分析法的分析[J].河北经贸大学学报，2017（3）：72-79. HUANG Sujian，LIQian，WANG Ji.A Comparative Evaluation on different ownership industrial enterprises'efficiency in China--analysis based on entropy weight method and grey relational analysismethod[J].Journal of Hebei University of Economics and Business，2017（3）：72-79.

[11]夏克文，李昌彪，沈钧毅.前向神经网络隐含层节点数的一种优化算法[J].计算机科学，2005（10）：143-145. XIA Kewen，LIChangbiao，SHEN Junyi.An Optimization algorithm on the number of hidden layer nodes in feed-forward neural network[J].Computer Science，2005（10）：143-145.

[12]向 燕，张小联，郑 鑫.基于BP神经网络的熔盐电导率预测研究[J].中国钨业，2014，29（3）：34-37. XIANGYan，ZHANGXiaolian，ZHENGXin.Electrical conductivity rate prediction ofmolten saltbased on BP neuralnetwork[J].China Tungsten Industry，2014，29（3）：34-37.

[13] SUN Tieqiang，CUIXuexie，ZHIQiqiu.Iron ore grinding energy conservation research based on neural network[J].Applied Mechanicsand Materials，2013，385/386（8）：1722-1725.

[14] CHEN Zhaoxia，HE Bailin，XU Xianfeng.Application of improved BP neural network in controlling the constant-Force grinding feed [J].Computer and Computing Technologies in Agriculture IV，2011，347（10）：63-70.

M ineral Processing Cost Prediction based on GRA-GSBP

YANGGang,WANGJianmin
(CollegeofElectricalEngineering,North ChinaUniversity ofScienceand Technology,Tangshan 063009,Hebei,China)

To solve the problems inmineralprocessing,includingmultiple affecting elements,coupling ornon-linear relationships existed among the factors,difficulty while determining the hidden layer nodes of BP neural network, this paper put forward an improved BPneuralnetwork cost forecastingmethod based on gray relationalanalysisand golden segmentation.Firstly,GRA is used to calculate the correlation between the factors and the cost of ore dressing,and then four variables which have the largest correlation are chosen as the inputs of the BP network. Secondly,the principle ofgolden segmentation isapplied to search the desired value in the region ofhistoricaldata. To obtain the number ofhidden layer nodeswhich can approachmore strongly,the regionwhere the desired number of hidden layer appears continually is expanded for higher precision.Finally,the data which have been stored in meter cabinetwere used to verify the cost forecastingmodel.The results showed that themethod can predict the trend ofmineralprocessing cost in real time.

grey relational analysis method;golden segmentation method;BP neural network;predict cost; correlation;thenumberofhidden layernodes

TP216

A

（编辑：刘新敏）

10.3969/j.issn.1009－0622.2017.03.013

2017-04-05

杨 刚（1992-），男，河北廊坊人，硕士研究生，主要研究方向为选矿信息化及控制理论的研究。

王建民（1958-），男，河北石家庄人，教授，主要从事选矿自动化及信息化的研究。