基于改进非负矩阵分解的肿瘤基因表达谱特征提取

黄经纬 杨国亮* 王艳芳 胡政伟

1(江西理工大学电气工程与自动化学院 江西 赣州 341000) 2(赣州市立医院信息技术科 江西 赣州 341000)



基于改进非负矩阵分解的肿瘤基因表达谱特征提取

黄经纬1杨国亮1*王艳芳2胡政伟1

1(江西理工大学电气工程与自动化学院 江西 赣州 341000)2(赣州市立医院信息技术科 江西 赣州 341000)

针对肿瘤基因表达谱的特点，提出基于低秩图正则非负矩阵分解(LGNMF)的特征提取方法，解决了NMF算法中缺少数据的全局信息，提升特征提取的有效性。该算法在NMF算法的基础上引入低秩图约束，提高了对数据局部和全局结构的描述，使得经过特征提取后的特征空间具有更强的分类能力。通过LGNMF算法对肿瘤基因表达谱数据集进行降维，获得低维特征空间，再使用KNN分类器对低维特征空间进行分类。通过与NMF、GNMF和RGNMF算法在四组标准肿瘤基因表达谱数据集进行对比，实验结果表明LGNMF算法能够有效提升分类效果。

低秩图 特征空间 肿瘤基因表达谱 特征提取

0 引 言

迄今为止，肿瘤仍然是人类难以完全攻克的病症。为此，人们迫切希望找到预防和治疗的方法。随着生物学及计算机的结合，医学疾病的诊治过程出现了依赖于微阵列技术而导出的大量肿瘤基因表达谱的新技术。

1999年，Golub等[1]率先发表了利用S2N作为指标对急性白血病亚型(Leukemia)进行分类，从此越来越多的人开始采用肿瘤基因表达谱进行分析和研究。受限于获取途径，其通常具有维数远远大于样本数量且具有冗余信息大的特点。由于实验是针对组织细胞进行，所有可检测的基因都被一一进行表示，但是实际上真实起决定性作用的基因只占其中小部分，从而导致肿瘤基因表达谱数据集过度冗余，造成“维数灾难”和“过拟合”[2]。为了解决前面所述的问题，维数约简[3]成为最行之有效的方法之一，受到了广大学者们的关注。维数约简是通过特征提取或者特征选择的方法来降低原始数据空间的维数。特征选择方法是指通过剔除原始数据空间中相关度低、冗余度高的特征，选取更具分类性能的特征子空间，以达到大幅度降低原始数据空间维数的目的，使得选取的特征子空间和分类目标含有高相关性，进而提升样本分类的准确率；而特征提取是对原始数据空间进行数学变换使其投影到新的低维特征空间，以获取尽可能少且分类能力强的特征空间，这样的特征空间可更好地描述基因数据[4-9]。

典型的特征提取方法主要有主成分分析(PCA)[6]、线性判别分析(LDA)[7]、非负矩阵分解(NMF)[8]等。NMF算法由于其特殊的非负特性，使得其被大量采用于处理各个范畴的问题。文献[10]中作者利用NMF算法对DNA微阵列进行分解达到降维的目的，但是NMF算法只考虑到数据的局部特性，忽略了数据的内在几何结构特性，从而影响特征提取的效果；文献[11]的作者为了使数据降维后仍可以保持原有数据点之间的相似性，在NMF的基础上添加了图正则约束，提高了特征提取的有效性。Kim[12]等对NMF算法进行改进，提出了稀疏NMF算法并且利用交替最小二乘法对其进行求解。文献[13]在NMF算法模型上同时添加了稀疏约束和图正则约束,从数据全局的角度来揭示数据点间的关系，大大提高了特征提取的能力。本文主要研究的是将NMF算法应用于肿瘤基因表达谱的特征提取，对NMF算法进行改进，添加了低秩图[12]约束，提出了基于低秩图正则非负矩阵分解算法。经实验验证，该算法在肿瘤基因表达谱分类问题上具有明显的优势。

1 非负矩阵分解模型

1.1 典型的NMF算法模型

NMF算法是对非负矩阵的一种线性的、非负的近似数据描述，对于给定的大小为m×n的原待分解矩阵X，其中m代表数据特征，n代表样本数目。通过NMF算法，将矩阵X分解成大小为m×r和r×n的矩阵H和W，它们都不含负元素，得到：

X≈HW

(1)

其中，H为基矩阵，W为系数矩阵，即W为原始矩阵X在基空间H上的投影，同时r的取值一般比m或n小，满足不等式r≤min(m,n)，使得矩阵H和W维数均低于原始矩阵X的维数。

利用X和HW之间的欧氏距离的平方构造代价函数，得到

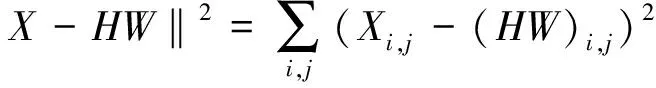
(2)

使用迭代的方法获得最小化‖X-HW‖2来得到W和H的解：

(3)

NMF算法由于其具备的非负特性，使得降维后的结果可以部分地表示向量空间的数据，具有局部性，然而却忽略了空间数据的内在几何结构特性，而空间数据的内在几何结构对聚类和分类问题却至关重要。文献[10]在NMF算法模型的基础上引入了图正则约束，提出了图正则非负矩阵分解算法，该算法克服NMF算法的局限性，获得了较好的分类效果。

1.2 图正则非负矩阵分解模型(GNMF)

GNMF[11]算法在NMF的基础上增加了图正则约束，这样即保留了NMF算法的局部稀疏性表示的优势，又使数据降维后仍可以保持原有数据点之间的相似性。其算法模型如下式所示：

(4)

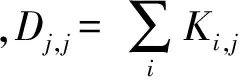
矩阵K定义如下：

(5)

其中Nk(xj)表示第j个样本k近邻；K表示对称矩阵。H和W的迭代更新公式如下式所示：

(6)

1.3 稀疏正则化NMF算法模型(RGNMF)

文献[13]分析了在图正则NMF模型的基础上添加稀疏正则项：

(7)

式中，hi表示H的行向量，e为单位列向量。文献[13]中对矩阵H的列和矩阵W的行加稀疏性正则，得到的目标函数如下式所示：

(8)

其中，L=D-K，通过对式(8)构造增广拉格朗日函数然后再分别对H和WT求导，最后由KKT条件得到乘法迭代公式如下：

(9)

添加了稀疏正则项的RGNMF算法与传统NMF算法相比，它能更好地发现稳定且直观的局部特征，并且能够按需求地调整分解后的矩阵的稀疏度大小。

2 低秩图正则非负矩阵分解(LGNMF)

2.1LGNMF模型

基于稀疏表示的RGNMF算法是从全局的角度来揭示数据点间的关系，揭示数据的全局结构信息。但是由于稀疏性约束条件，通常只有很少的一部分全局信息能够被表示出来，不仅如此，当数据集存在一定噪声[9]干扰时，稀疏图表示数据信息的能力就会受到影响。

低秩图[14-15]是揭示数据全局信息的一种结构图，具有更好的数据局部和全局描述能力，基于低秩图的维数约简方法是一种更为有效的特征提取方法。非负矩阵分解模型没有考虑分解后数据特征空间的低秩特性，这种低秩特性在一定程度上反映了数据空间的全局结构特征，有利于进行基因特征提取[16]。为此，本文在普通NMF基础上，引入低秩图正则约束，构建模型如式(10)所示：

(10)

其中，X为肿瘤基因表达谱数据集，H为投影空间一组基向量，W为投影坐标矩阵(或回归系数矩阵)，由于同类样本在特征空间的投影坐标相似，故具有低秩特性，‖W‖*项为低秩约束项，tr(WLWT)为图正则项，L为图拉普拉斯矩阵，α、β为平衡参数。

2.2LGNMF模型求解

令W=J，对式(10)构建增广拉格朗日函数如下：

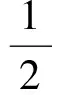
tr(Y2HT)+tr(Y3WT)=

βtr(WLWT)+tr((Y1)T(W-J))+

tr(Y2HT)+tr(Y3WT)

(11)

其中，Y1、Y2和Y3表示拉格朗日算子，μ>0为常数。利用迭代方法求解最优的(H，W，J)，由于目标函数式(11)中待求解的参数较多，我们无法一次性得出所有参数的最优解，通过采用交替求解策略，固定其他参数，分别对每个参数进行独立的更新。

更新H，固定W和J，目标函数(11)可以简化成下式：

(12)

式(12)可通过求极小值的方法进行求解，首先对式(12)进行求导得：

(13)

更新W，固定H和J，目标函数式(11)可简化为

Compared with the sham group,the femoral BMD in the OVX group was significantly decreased.Compared with the OVX group,the esculetin group had significantly greater femoral BMD.However,the esculetin group still had a lower femoral BMD than the sham group(Table 1).

(14)

同理，式(14)可通过求极小值的方法进行求解，首先对式(14)进行求导得：

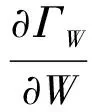
(15)

由KKT条件得到H和W的乘法迭代公式如下：

(16)

更新J，固定H和W，目标函数式(11)可简化为

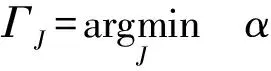
(17)

式(17)的求解采用奇异值阈值算法获取最佳目标值。其解为：

(18)

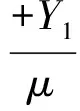
S(∑)=max(∑ii,0)

(19)

拉格朗日算子Y1的迭代公式为Y1=Y1+μ[W-J]。

3 LGNMF算法描述

结合第2节对算法模型的求解，下面给出基于LGNMF的分类算法描述。

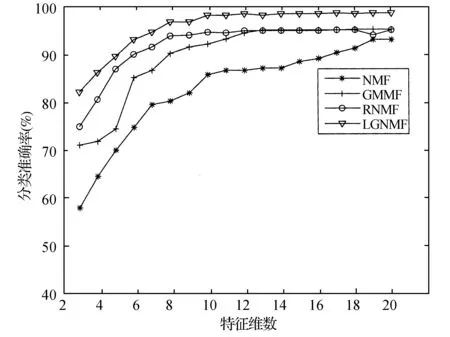
算法名称：基于LGNMF的肿瘤基因表达谱分类输入：肿瘤基因表达普数据矩阵X，参数λ和β，子空间维数k初始化：H=abs(rand(m，k))；W=abs(rand(k，n))；J=abs(rand(k，n))；Y1=abs(rand(k，n))；max＿mu=106；mu=10-1；rh0=1．21．根据式(16)更新H和W矩阵；2．根据式(18)迭代更新J；3．更新拉格朗日算子Y1=Y1+μW-J[]；4．mu=min(max＿mu，mu∗rh0)；5．iter=iter+1，当iter

4 实验结果及分析

4.1 实验数据与实验环境

本实验采用四个公共的数据集，如表1所示。

表1 实验数据集的描述

(1) DLBCL数据集包含了77个样本，5 469个基因，分为DLBCL和FL两个子集，其中DLBCL样本数为58，FL样本数为19；

(2) Prostate数据集由52个癌症样本和50个正常基因样本，共10 509个基因；

(4) NCI数据集包含了66个样本，2 308个基因，分为四类：第一类有23个样本，第二类有8个样本，第三类有15个样本，第四类有20个样本。

本实验采用的实验环境配置为：计算机的配置为3.2 GHz的Intel Core i5-3470 CPU，4 GB RAM，运行Matlab R2013a。

4.2 实验结果分析

通过对比NMF、GNMF、RGNMF、LGNMF算法在DLBCL、Prostate、Leukemia、NCI四个不同的表达谱数据集上的分类情况来验证LGNMF算法的可行性和有效性。实验过程中，我们将原始数据集根据1∶1的比例分为训练集和测试集。用分类准确率 (Accurate)来精确区分算法的优劣性，可定义如式(20)所示，实验在每种目标特征维数下进行15次，取Accurate值[17]的平均值作为实验结果。

(20)

其中，Tright为测试集中被正确分类的样本数，T为测试集当中总的样本数。

4.2.1 DLBCL数据集实验结果分析

DLBCL数据集由两类总计77个样本组成，有5 469个基因。本实验通过NMF、GNMF、RGNMF和本文提出的低秩图正则非负矩阵分解(LGNMF)算法对DLBCL数据集进行特征提取，使其维度依次降到如图1所示维数，再利用KNN分类器对其进行分类，通过对比实验来验证LGNMF算法的有效性。

特征提取的主要目的是为了有效地减少数据的维数，促使某些算法在低维数据上能够更加快速有效的进行，同时又不影响数据内在属性的表达能力。为了验证本文提出的特征提取算法的性能，图1中列出了包括本文算法在内四种算法在不同维数下的分类表现结果。

图1 不同算法在DLBCL上分类表现

如图1所示的曲线图，横坐标为肿瘤基因表达谱经特征提取降维后的特征维数，纵坐标为分类准确率，通过对比四种算法的分类结果可以看出：(1) 随着特征维数的不断上升，四种算法表现出分类准确率不断攀升的现象。图中维数达到20时，四中算法都获得了不错的效果，准确率均能保持在90%以上，其中LCNMF算法获得了98.45%的准确率，为四种算法最高；(2) LGNMF算法在20、10、5、3特征维数下的分类效果均优于其他三种算法，并且随着特征维数的减少，其优势越发的明显，当特征维数降到3维时，其分类准确率仍能达到80%以上。通过DLBCL数据集实验证明，低秩图正则非负矩阵分解(LGNMF)算法在肿瘤基因表达谱数据集分类中相比于其他算法更具有优势。

4.2.2 Prostate数据集实验结果分析

Prostate数据集有52个癌症样本和50个正常样本，共10 509个基因。本实验同样通过NMF、GNMF、RGNMF和LGNMF算法对Prostate数据集进行特征提取，使其维度依次降到如图2所示维数，再利用KNN分类器对其进行分类，四种算法对应的准确率如图2所示。

图2 不同算法在Prostate上分类表现

从图2中可以看出：(1) 对于Prostate数据集，四种算法对分类的影响在维数范围处于10到20之间的效果比较接近，在维数为20时，效果最好，除了NMF算法的分类准确率稍低，其余算法的分类准确率均达到了96%；(2) 低秩图正则非负矩阵分解(LGNMF)算法在大多数特征维数下的分类效果均优于其他三种算法，并且随着特征维数的减少，其优势越发的明显，当特征维数降到3维时，其分类准确率仍能达到80%。通过DLBCL数据集实验证明，低秩图正则非负矩阵分解(LGNMF)算法在肿瘤基因表达谱数据集分类中相比于其他算法更具有优势。

4.2.3 Leukemia数据集实验结果分析

Leukemia数据集分为三类，由72个样本组成，每个样本具有5 327个基因。本实验分别以NMF、GNMF、RGNMF和LGNMF算法作为特征提取方法，将NCI数据集降维到图3所示，再利用KNN分类器对其进行分类，通过对比实验来验证LGNMF算法的有效性。

图3 不同算法在Leukemia上分类表现

从图3中可以看出：(1) 相较于Prostate和DLBCL，LGNMF算法在Leukemia数据集上的Accurate值最高，达到98%。当特征维数降到10时，其他三种算法的Accurate值都有所下降，但LGNMF的分类准确率仍然能够保持95%左右，说明经LGNMF算法处理的数据具有更高的分类能力；(2) LGNMF算法在20、10、5、3特征维数下的分类效果均优于其他三种算法，并且随着特征维数的减少，其优势越发的明显，当特征维数降到3维时，其分类准确率仍能达到82%。通过DLBCL数据集实验证明，低秩图正则非负矩阵分解(LGNMF)算法在肿瘤基因表达普数据集分类中相比于其他算法更具有优势。

4.2.4 NCI数据集实验结果分析

NCI数据集有4个种类，共含66个样本，2 308个基因。本实验分别以NMF、GNMF、RGNMF和LGNMF算法作为特征提取方法，对NCI数据集进行降维，使其维度依次降到如图4所示，再利用KNN对其进行分类检测，再通过对比检验LGNMF算法的有效性。图4为NMF、GNMF、RGNMF和LGNMF算法在Prostate数据集上的分类结果。

图4 不同算法在NCI上分类表现

从图4中可以明显地发现添加了图正则约束的NMF算法比普通的NMF算法分类效果好，添加了稀疏约束的图正则的NMF算法比图正则非负矩阵分解分类准确率更高，而本文提出的低秩图正则非负矩阵分解(LGNMF)算法明显优于其他三种特征提取方法。且对于抗特征维数的降低带来的分类准确性下降的能力相对更强，在维数为20时，各算法往往能够取得最好的分类效果，此时，LGNMF的效果处于领先位置。

综合以上四个实验结果可以得出：在四个肿瘤基因表达谱数据集上，LGNMF的分类准确率均比NMF、GNMF和RGNMF方法高，特别在Prostate数据集上，其分类准确率高达98%。当特征维数降到8后，NMF、GNMF和RGNMF算法的效果出现率明显下滑，但是LGNMF算法的分类准确率仍然能够达到80%以上，说明本文提出的基于低秩图正则非负矩阵分解(LGNMF)的基因表达谱数据特征提取算法是有效且稳定的。

5 结 语

本文提出了一种基于低秩图正则非负矩阵分解(LGNMF)的基因表达谱数据特征提取算法。该算法在NMF的基础上引入低秩图的概念，低秩图具有更好的数据局部和全局描述能力，基于低秩图的维数约简的思路是一种更为有效地特征提取方法。考虑到分解后肿瘤基因表达谱数据特征空间的低秩特性，这种低秩特性在一定程度上反映了数据空间的全局结构特征，有利于特征提取。同NMF、GNMF和RGNMF算法相比较，LGNMF在肿瘤基因表达谱数据集的分类任务中表现出更大优势。尤其在特征维数越低的情况下，优势更加明显，体现了LGNMF特征提取算法能够更加有效地提升模式识别中分类算法的性能。

[1] Golub T R, Slonin D K, Golub T R, et al. Molecular classification of cancer [J]. Journal of Clinical Microbiology, 1999, 93(5):1210-1220.

[2] Brock G N, Shaffer J R, Blakesley R E, et al. Which missing value imputation method to use in expression profiles: a comparative study and two selection schemes [J]. Bmc Bioinformatics, 2008, 9(2):1-12.

[3] Espezua S, Villanueva E, Maciel C D, et al. A Projection Pursuit framework for supervised dimension reduction of high dimensional small sample datasets[J]. Neurocomputing, 2015, 149(PB):767-776.

[4] 苏雅茹. 高维数据的维数约简算法研究[D]. 合肥：中国科学技术大学, 2012.

[5] Gan B, Zheng C H, Zhang J, et al. Sparse representation for tumor classification based on feature extraction using latent low-rank representation.[J]. Biomed Research International, 2014, 2014(10):63-68.

[6] Bro R, Smilde A K. Principal component analysis[J]. Analytical Methods, 2014, 6(6):433-459.

[7] Valle D, Baiser B, Woodall C W, et al. Decomposing biodiversity data using the Latent Dirichlet Allocation model, a probabilistic multivariate statistical method[J]. Ecology Letters, 2014, 17(12):1591-1601.

[8] Tan C S, Ting W S, Mohamad M S, et al. A Review of Feature Extraction Software for Microarray Gene Expression Data[J]. Biomed Research International, 2014, 2014:213656-213656.

[9] 杨国亮, 鲁海荣, 唐俊,等. 基于迭代对数阈值的加权 RPCA非局部图像去噪[J]. 江西理工大学学报, 2016, 37(1):57-62.

[10] 张东波. 基于非负矩阵分解的基因数据子空间分类研究[D]. 西安电子科技大学, 2005.

[11] Cai D, He X, Wu X, et al. Non-negative Matrix Factorization on Manifold[C]//Eighth IEEE International Conference on Data Mining. IEEE Computer Society, 2008:63-72.

[12] Kim H, Park H. Sparse non-negative matrix factorizations via alternating non-negativity-constrained least squares for microarray data analysis.[J]. Bioinformatics, 2007, 23(12):1495-1502.

[13] 沈永康. 非负矩阵分解的稀疏性模型及初始化研究[D]. 浙江大学, 2011.

[14] Zhuang L, Gao H, Huang J, et al. Semisupervised classification via low rank graph[C]//Image and Graphics (ICIG), 2011 Sixth International Conference on. IEEE, 2011: 511-516.

[15] Zhang N, Yang J. Low-rank representation based discriminative projection for robust feature extraction[J]. Neurocomputing, 2013, 111(6):13-20.

[16] Cui Y, Zheng C H, Yang J. Identifying Subspace Gene Clusters from Microarray Data Using Low-Rank Representation [J]. Plos One, 2012, 8(3):e59377.

[17] 潘江山, 陈晓云, 董红玉. 基于INCA的肿瘤基因表达谱分类模型[J]. 福州大学学报:自然科学版, 2014, 42(4):639-645.

FEATUREEXTRACTIONOFTUMORGENEEXPRESSIONPROFILESBASEDONIMPROVEDNON-NEGATIVEMATRIXFACTORIZATION

Huang Jingwei1Yang Guoliang1*Wang Yanfang2Hu Zhengwei1
1(SchoolofElectricalEngineeringandAutomation,JiangxiUniversityofScienceandTechnology,Ganzhou341000,Jiangxi,China)2(DepartmentofInformationEngineering,GanzhouMunicipalHospital,Ganzhou341000,Jiangxi,China)

According to the characteristics of the tumor gene expression profiles, we proposed a feature extraction algorithm, based on low-rank graph non-negative matrix factorization (LGNMF). It solved the lack of information on the global structure data of NMF algorithm and promoted the validity of feature extraction. The algorithm had improved the description of local and global data structures, based on NMF algorithm with low-rank graph constraints, which made feature space have stronger classification ability after feature extraction. The low-dimensional feature space was obtained by LGNMF algorithm, and it was classified by KNN classifier. We compared with the NMF, GNMF and RGNMF algorithm in four groups of standard tumor gene expression profile data sets. The experimental results show that LGNMF algorithm can improve the effect on classification.

Low-rank graph Feature space Tumor gene expression profile Feature extraction

2016-09-25。国家自然科学基金项目(51365017,61305019);江西省教育厅科技计划项目(GJJ150680)。黄经纬，硕士生，主研领域：机器学习与模式识别。杨国亮，教授。王艳芳，硕士。胡政伟，硕士生。

TP391.41

A

10.3969/j.issn.1000-386x.2017.08.045