一种求解姿态不可交换误差补偿系数的通用方法

严恭敏，杨小康，翁 浚，秦永元

(西北工业大学自动化学院，西安 710072)



一种求解姿态不可交换误差补偿系数的通用方法

严恭敏，杨小康，翁 浚，秦永元

(西北工业大学自动化学院，西安 710072)

针对捷联惯导姿态更新算法中的不可交换误差补偿系数求解问题，论文在多项式角运动条件下建立了角速度多项式、角增量多项式与多子样角增量采样之间的线性关系，根据等效旋转矢量微分方程中不可交换误差多项式的向量叉乘特点，将叉乘转化为多项式系数的卷积运算，推导给出了计算任意子样数不可交换误差补偿系数的数值方法，新方法易于软件编程实现。最后，通过仿真计算给出了2～6子样误差补偿系数，其中2～4子样结果与已有文献完全相同，而5、6子样为首次给出。

捷联姿态更新算法；等效旋转矢量；不可交换误差；数值解

0 引 言

目前，捷联惯导系统的姿态更新算法中普遍采取的思路是[1-2]：根据不可交换误差补偿算法，使用陀螺角增量的多子样采样构造等效旋转矢量，尽量消除转动不可交换误差，再利用等效旋转矢量计算姿态更新四元数，实现姿态更新。等效旋转矢量多子样算法的数学理论基础是等效旋转矢量微分方程(Bortz方程)[3]。由Bortz方程求解多子样不可交换误差补偿系数的方法主要有两类：一是在纯圆锥运动假设条件下求解的所谓优化圆锥误差补偿系数，该问题业已得到了比较圆满的解决，理论上获得了求解任意子样系数的通式[4-6]；二是在多项式角运动假设条件下，基于等效旋转矢量泰勒级数展开法的不可交换误差补偿系数求解，虽然研究者们求得了一系列不同子样数的误差补偿系数[7-10]，甚至有研究者考虑了Bortz方程不可交换误差高阶项的影响，提出了高阶补偿算法[11]，但是目前还没有得到这些方法的求解通式，每当遇到一种新的子样数算法就得重新推导补偿系数，特别在高子样数情况下，推导过程异常繁琐。

在多项式角运动条件下，论文放弃了传统的冗长而繁琐的公式推导思路，而通过仔细分析基于等效旋转矢量泰勒级数展开法求解不可交换误差补偿系数的特点，给出了求解补偿系数的通用数值算法，新算法简洁，易于软件编程实现。论文求解不可交换误差系数的方法与传统方法相比，基本理论是一样的，都是基于Bortz方程的一阶近似，在圆锥误差积分中以角增量代替等效旋转矢量，通过角速度的多项式假设和等效旋转矢量的泰勒级数展开，比较级数低阶项与角增量叉乘的系数，联立起来建立方程组，从而求得误差补偿系数；但是论文提出的数值求解方法，在建立方程组和求解系数时都非常方便，省去了传统采用公式直接推导的繁琐，具有很好的通用性。论文通过仿真计算，首次正确给出了5子样和6子样误差补偿系数。

1 角运动的多项式表示

在实际捷联惯导系统中，大多数陀螺采样直接获得的是角增量信息，而姿态等效旋转矢量更新算法的推导过程需要用到角速度作为输入，因此，在角运动为多项式形式假设条件下先给出由角增量信息构造角速度的方法。

假设角速度ω(t)为关于时间t的(N-1)次多项式，即

(1)

式中：wj(j=N-1,N-2,…,0)为列向量，Wi(i=x,y,z)为行向量，W为3×N系数矩阵。

对式(1)积分，可得相对于0时刻的总角增量为

(2)

式中：aj为列向量且有aj+1=wj/(j+1)，Ai为行向量，A为3×N系数矩阵。

假设陀螺采样间隔为h，在时间段(-ph,nh]内进行了N次角增量采样(p≥0,n>0且p+n=N)，分别记为Δθj(j=-p+1,-p+2,…,n)，对角速度积分可得角增量采样，如下

wN-2+…+(tj-tj-1)w0

(3)

式中：简记tj=jh，当tj>0时表示当前姿态更新周期内的角增量采样；而当tj≤0时表示利用了前面姿态更新周期的角增量信息。

根据式(3)，将相继N次角增量采样合并在一起写成矩阵形式，有

Θ=WΓ

(4)

式中：记

由式(4)容易求解得到以角增量表示的多项式系数矩阵

W=ΘΓ-1

(5)

由此可见，根据相继的N次角增量采样，通过式(5)和式(1)可以构造一个N-1次的多项式角速度拟合；显然，角速度系数wj及角增量系数aj都是所有角增量采样Δθj的线性函数。

2 不可交换误差与补偿系数之间关系推导

等效旋转矢量微分方程(Bortz方程)为[3]：

[φ(t)×]2ω(t)

(6)

式(6)在理论上严格成立，但较复杂，不便于工程使用，通行的做法是将右端第三项视为小量，并将第二项中的等效旋转矢量近似为角增量，从而近似有

(7)

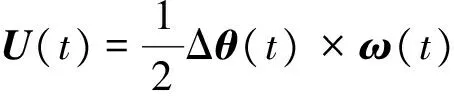
若将式(1)和式(2)的列向量系数多项式表示法代入式(7)，可得

(8)

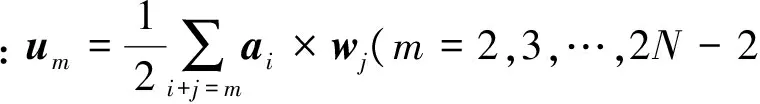
由式(1)和式(2)的行向量系数多项式表示法代入式(7)，考虑到叉乘运算规则，可得

(9)

式中：运算符“*”表示两多项式系数向量之间的卷积运算。与式(8)相比，利用式(9)卷积计算系数矩阵U较方便。

记T=nh为等效旋转矢量更新周期，将φ(T)在时间t=0处展开成泰勒级数，考虑到φ(0)=Δθ(0)=0及式(7)、式(8)，则有

(10)

式(10)移项，可得

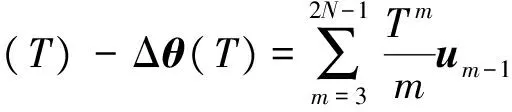
(11)

由第1节分析可知，wj和aj均为角增量采样Δθj的线性函数；由式(8)可知，um可表示为ai和wj叉乘和，因此um可以表示为各个角增量Δθj之间的叉乘和形式，从而有

(12)

简记为

ε=bK

(13)

(14)

从式(14)可求得误差补偿系数向量K的最小二乘解

K=(BTB)-1BTE

(15)

3 仿真与分析

综合第1～2节的公式推导，下面给出求解不可交换误差补偿系数的详细步骤：

1)按需求给定子样数N(包括p和n的值)，不妨将等效旋转矢量更新周期作归一化处理，即令T=1和h=1/n，预先计算式(4)中的系数矩阵Γ和Γ-1备用；

3)根据式(9)卷积计算系数矩阵U；

4)根据式(12)或式(13)计算不可交换误差ε和角增量叉乘矩阵b，确定一个量测方程；

5)重复步骤2～4，建立一组如式(14)的量测方程组，一般可选择l=N；

6)按式(15)求解不可交换误差补偿系数向量K，完毕。

按照上述步骤，编写了MatlabPSINS工具箱仿真计算程序[12]，表1列出了子样数N=2～6(p=0)的仿真结果，为简洁，误差补偿系数kij仅保留了6位小数，完全可满足实际应用对算法精度的要求。若不计数值表示的舍入误差，表1中2～4子样结果与文献[4,7-10]的结果完全一致(文献中通常以分数形式给出)。传统基于等效旋转矢量泰勒级数展开法求解误差补偿系数的理论思路并不复杂，但公式推导过程比较繁琐，文献[13]给出了5子样的推导过程。然而与本文相比,文献[13]中式(20)明显是错的，原因在于文献[13]中式(10)的系数推导失误，1/12应为1/14。本文求解误差补偿系数的方法和软件编程更简便，表1列出了6子样误差补偿系数，读者还可根据需要任意设置子样数N(包括p和n)，运行程序后便可立即得到相应的系数，避免了繁琐的公式推导过程。

表1 2～6子样不可交换误差补偿系数

从表1不难看出，对于任意一子样数N(p=0)，不可交换误差补偿系数存在对称性，即有ki,j=kN-j+1,N-i+1，以6子样为例，将表1中的6子样系数重新整理成表2形式，可见误差系数关于副对角线是对称的。

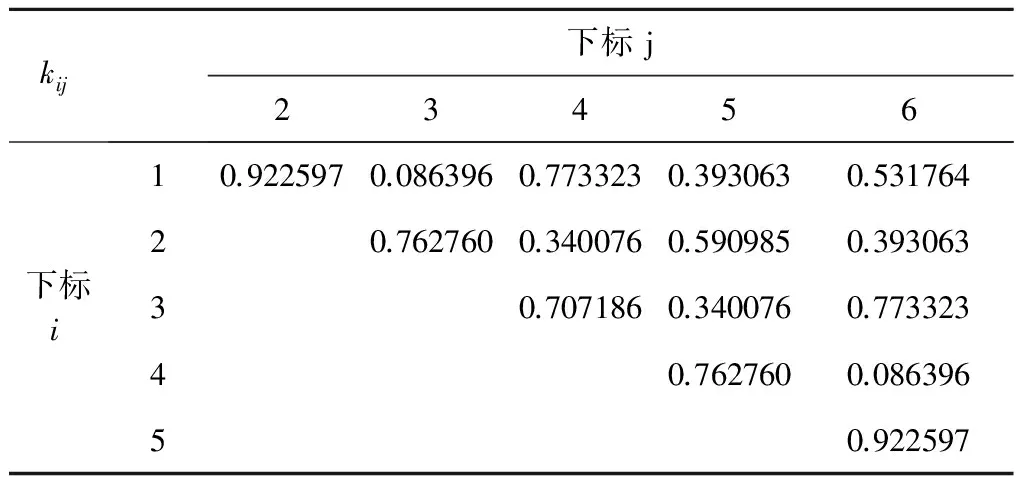
表2 6子样系数的对称性

4 结 论

在传统的捷联惯导姿态不可交换误差补偿算法中，不论是基于纯圆锥运动假设的优化算法还是基于多项式角运动的一般补偿算法，都是在一定近似假设条件下进行推导的，比如前者假设锥角为小角度而后者忽略了Bortz方程中高阶项的影响，从而使得结果也是近似的，特别对于高子样算法而言，其误差补偿往往达不到理论宣称的效果，有时高子样算法的精度反而不如低子样算法[14]。显然，片面追求高子样数的算法是不合适的，不一定能带来实用效果的明显改善。但是，从理论研究角度看，本文给出了求解各种子样数误差补偿系数的通用方法，为实际应用和算法选择提供了更多的参考和便利。

[1]SavagePG.Strapdowninertialnavigationintegrationalgorithmdesignpart1:attitudeagorithms[J].JournalofGuidance,Control,andDynamics, 1998,21(1): 19-28.

[2] 周江华,苗育红,肖刚. 扩展旋转矢量捷联姿态算法[J]. 宇航学报, 2003, 24(4): 414-417.[ZhouJiang-hua,MiaoYu-hong,XiaoGang.Extendedrotationvectorbasedstrapdownattitudealgorithms[J].JournalofAstronautics, 2003, 24(4): 414-417.]

[3]BortzJE.Anewmathematicalformulationforstrapdowninertialnavigation[J].IEEETransactionsonAerospaceandElectronicSystems, 1971, 7(1): 61-66.

[4]IgnagniMB.Efficientclassofoptimizedconingcompensationalgorithms[J].JournalofGuidance,Control,andDynamics, 1996, 19(2): 424-429.

[5]ParkCG,KimKJ,LeeJG,etal.Formalizedapproachtoobtainingoptimalcoefficientsforconingalgorithms[J].JournalofGuidance,Control,andDynamics, 1999, 22(1): 165-168.

[6]TangCY,ChenXY.Ageneralizedconingcorrectionstructureforattitudealgorithms[J].MathematicalProblemsinEngineering, 2014:1-15.

[7]MillerR.Anewstrapdownattitudealgorithm[J].JournalofGuidance,Control,andDynamics, 1983, 6(4): 287-291.

[8]LeeJG,YoonYJ,MarkJG,etal.Extensionofstrapdownattitudealgorithmforhigh-frequencybasemotion[J].JournalofGuidance,Control,andDynamics, 1990, 13(4): 738-743.

[9] 王立冬，孟亚峰，高庆. 基于角增量和角速率的旋转矢量算法的等效性[J]. 宇航学报, 2014, 35(3): 340-344.[WangLi-dong,MengYa-feng,GaoQing.Equivalenceanalysisofrotationvectoralgorithmbasedonangleincrementandangularvelocity[J].JournalofAstronautics, 2014, 35(3): 340-344.]

[10] 张泽,段广仁. 捷联惯导四子样旋转矢量姿态更新算法[J]. 控制工程, 2010, 17(3): 272-274.[ZhangZe,DuanGuang-ren.Onfour-samplerotationvectoralgorithmforSINSattitudeupdating[J].ControlEngineeringofChina, 2010, 17(3): 272-274.]

[11]WangMS,WuWQ,WangJL,etal.High-orderattitudecompensationinconingandrotationcoexistingenvironment[J].IEEETransactionsonAerospaceandElectronicSystems, 2015,51(2):1178-1190.

[12] 严恭敏. 高精度捷联惯性导航系统Matlab工具箱[EB/OL]. (2013-09-16) [2017-2-20].http://blog.sina.com.cn/s/blog_40edfdc90101heg0.html.

[13] 靳聪,赵修斌,许云达,等. 捷联姿态解算五子样等效旋转矢量算法研究[J]. 科学技术与工程, 2014, 14(29): 96-99.[JinCong,ZhaoXiu-bin,XuYun-da,etal.Researchonfive-samplealgorithmforattitudeupdatingofSINS[J].ScienceTechnologyandEngineering, 2014, 14(29): 96-99.]

[14] 严恭敏,严卫生,徐德民. 经典圆锥误差补偿算法中剩余误差估计的局限性研究[J]. 中国惯性技术学报, 2008, 16(4): 379-385.[YanGong-min,YanWei-sheng,XuDe-min.Limitationsoferrorestimationforclassicconingcompensationalgorithm[J].JournalofChineseInertialTechnology, 2008, 16(4): 379-385.]

通信地址：陕西省西安市西北工业大学自动化学院183号信箱(710072)

电话：(029)88431369

E-mail:yangongmin@163.com

A General Method to Obtain Noncommutativity Error Compensation Coefficients for Strapdown Attitude Algorithm

YAN Gong-min, YANG Xiao-kang, WENG Jun, QIN Yong-yuan

(School of Automation, Northwestern Polytechnical University, Xi’an 710072, China)

In a strapdown attitude updating algorithm, a general numerical method for obtaining the multi-sample noncommutativity error compensation coefficients is presented. Under the condition of the angular motion expressed as polynomial, the linear relationships between the angular velocity polynomial, angular increment polynomial and multi-sample angular increments are established in this paper. According to the vector cross product operation of the noncommutativity error polynomial in the equivalent rotation vector differential equation, the cross product is converted into the convolution operation of the polynomial coefficients. Then, the numerical methods to compute the noncommutativity error compensation coefficients of the arbitrary multiple samples are presented in deduction, which are easy to be implemented with computer programming. Finally, simulations are carried out to obtain the 2～6-sample compensation coefficients, in which the 2～4-sample coefficients are consistent with the existing literatures and the 5 or 6-sample coefficients are firstly proposed by the authors.

Strapdown attitude algorithm; Equivalent rotation vector; Noncommutativity error; Numerical solution

2017-03-14;

2017-05-15

航空科学基金(20165853041)

V249.3

A

1000-1328(2017)07-0723-05

10.3873/j.issn.1000-1328.2017.07.000

严恭敏(1977-)，男，博士，副教授，主要从事惯性导航与信息融合理论研究。