一种面向增材制造技术的桁架式支架结构设计方法

李修峰，高令飞，王 伟，王浩攀

(中国空间技术研究院通信卫星事业部，北京 100094)



一种面向增材制造技术的桁架式支架结构设计方法

李修峰，高令飞，王 伟，王浩攀

(中国空间技术研究院通信卫星事业部，北京 100094)

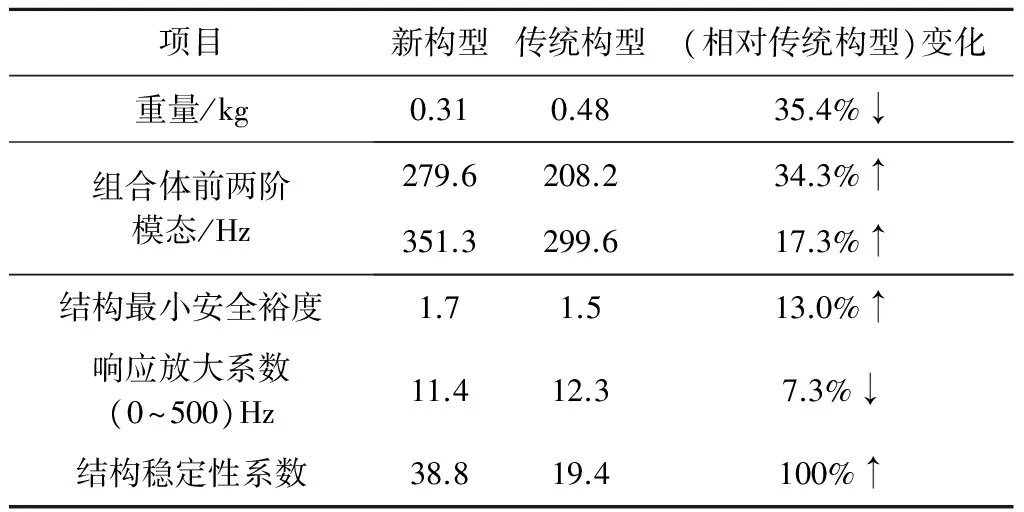
针对卫星结构轻量化设计需求，综合应用拓扑优化方法和增材制造技术在结构设计和加工方面的优势，提出一种面向增材制造的桁架式支架结构设计方法。首先，考虑增材制造加工工艺约束，应用拓扑优化方法在结构可行设计空间中寻找最佳传力路径，以此为基础抽象出相对应的桁架结构；然后，应用尺寸优化方法，设计最优的桁架杆件截面尺寸；最后，综合考虑最优杆件尺寸和结构加工/使用约束，进行几何重构，获得可供增材制造的结构设计方案。将方法应用于某卫星敏感器支架结构设计，得到一种相对传统构型减重35.4%的轻量化设计方案。经详细力学分析验证，在使用与传统构型支架相同材料参数和载荷工况下，新型支架基频提高34.3%，安全裕度提高13.0%，同时动态响应系数降低7.3%，验证了方法在结构设计方面的可行性，为同类结构的轻量化设计提供了有益参考。

卫星；支架；结构优化；增材制造；桁架结构

0 引 言

随着航天技术的深入发展和广泛应用，航天项目带动的产业价值日益凸显，与之相关的成本支出也得到了越来越多的重视。相关统计表明，航天器质量每减轻1 kg，其成本大约能降低10000美元[1]。航天器的轻量化设计已成为未来航天技术发展的战略目标之一。

结构分系统是航天器的主要组成部分之一，占航天器整体重量的比例约为7%～10%[2]，因而由结构分系统的轻量化设计带来的减重效益是相当可观的。实现结构轻量化的途经主要有使用轻质材料和优化设计构型两种。目前，适用于航天器结构的常用材料主要有铝合金、镁合金、钛合金以及各种类型的复合材料等[3-4]。随着工业技术的发展，铝锂合金(密度2.3～2.4 g/cm3)和镁锂合金(密度1.35～1.65 g/cm3)也逐渐进入航天工程领域。然而，当材料轻质化潜力挖掘到一定程度后，结构进一步轻量化的目标最终还需依赖构型优化设计实现。

一直以来，结构优化设计方法特别是拓扑优化方法是获得结构最佳(轻量化)构型一种成熟且较为有效的方法，连续体结构拓扑优化方法主要有均匀化方法、变密度方法和渐进结构优化方法[5-7]。变密度法是将每个单元的相对密度作为设计变量，并在材料弹性模量与相对密度间建立一种数学关系，进而使用基于连续变量的算法进行优化迭代。该方法适合结构刚度最大化、频率最大化、多目标拓扑优化设计等结构优化问题[8]，目前已在汽车、航空及航天等重视产品重量指标的工程领域中得到广泛应用。如北美汽车钢铁联盟开展的福特汽车SUV车架轻量化设计，实现了23%的减重，与此同时扭转刚度提高了30%[9]；空客A380型客机机翼前缘肋板结构减重设计，实现了单架飞机500 kg的减重[10]。洛马公司进行卫星主承力构件优化分析，采用箱式承力结构取代承力筒式结构，实现卫星减重40%[11]。值得注意的是，在指定载荷与边界条件下，拓扑优化给出的最佳传力路径常常是一种类似植物根系的结构，而这种结构在传统加工工艺(如机加工、铸造、锻造和挤压等)下，通常是无法实现的。因此，设计师不得不在最佳构型的基础上兼顾传统制造工艺的可行性，采用内腔简单、形状规则的结构形式重新构造拓扑优化结果。最终的结构设计方案虽然在一定程度上提高了材料的利用效率、降低了结构重量，但材料利用潜力仍远不止于此。在传统制造工艺阶段，如何降低工艺约束对结构轻量化设计的影响已成为一个无法克服的问题。

如今，这一问题在增材制造技术出现后迎刃而解。增材制造技术不需要传统的刀具、机床、夹具，直接以三维数字模型文件为基础便可快速而精密地制造出任意复杂形状的新产品、模具或模型[12]。该技术的出现为复杂构型制造提供了可能，通过将材料尽可能的堆叠到结构承载路径上，解放了传统制造工艺约束，进一步提升了材料使用效率，为结构优化设计结果的直接应用开拓了一种新的途径。增材制造技术在复杂构型制造方面的巨大优势引起了国外大型航空航天制造企业和国家研究机构(如洛马、空客、欧洲防务公司、美国圣地亚国家实验室等)的广泛关注，目前已在导弹控制舱外壳、飞行器支架等承力构件研制中开展应用研究[13]。

当前成熟的增材制造工艺是一种增材与减材结合的工艺过程，一般分为前处理、成型以及后处理三个部分。前处理主要进行零件模型数据转换，即将三维模型转化为增材制造机器能够识别的格式，然后对其进行切片以及添加支撑结构的处理；成型指增材制造设备通过堆叠操作将成型材料制作成需要的模型；后处理指对成型零件减材加工以满足设计需要，主要包括支撑材料去除、局部打磨以改善表面质量等。辅助支撑结构作为实现悬空特征堆叠成型和降低零件翘曲变形的主要手段，是增材制造工艺区别于传统加工工艺的显著特点，是否具备可行的辅助支撑结构方案，是进行基于增材制造工艺的结构设计需要考虑的主要工艺约束。

针对卫星结构轻量化设计需求，结合拓扑优化设计方法的结构构型设计优势和增材制造技术的复杂结构加工成型优势，本文提出一种面向增材制造技术的桁架式支架结构设计方法。为验证设计方法的可行性，文中以某敏感器支架为研究对象，在详细分析其功能与性能约束的基础上，开展了支架结构轻量化设计，并从重量指标及力学性能(包括刚度、强度、动力学响应以及稳定性)方面与传统支架构型进行了对比分析。

1 结构设计策略

结构构型设计的本质是其承载路径的优化设计，即根据结构的承载特点，寻求结构中最佳的承载路径，并将其通过最简单、最直接的几何特征表达出来。拓扑优化是研究承载结构内部传力路径分布的一种有效方法，针对拓扑优化结果中存在很多不规则孔洞、复杂形状、锯齿形边界、灰色单元等细小特征，目前常用开孔(即采用规则几何形状的孔洞以及B样条曲线来对结构特征内、外边界进行识别)和类桁架重构(即采用桁架式的结构再现承载路径)的方式进行结果解读。桁架式结构整体刚度性能良好，通过合理设计桁架走向、截面形状和尺寸可实现结构承载能力的合理分配，材料承载效率高[14]，适合用作星上质量集中且安装接口简单的设备承力结构构型。

金属增材制造技术根据粉末材料输送方式的不同，可分为铺粉和送粉两种累积制造技术。铺粉增材技术成形的零件精度较高，适合于制造体积较小、形状复杂的工件，由于该技术在熔化金属粉末时，零件内部产生较大的热应力，容易产生开裂问题。因此，在进行基于铺粉制造工艺的结构设计时，应充分考虑以下三种制造工艺约束：1)结构最大外形尺寸约束；2)复杂特征的加工可行性，或可以理解为支撑结构增加和去除的可行性；3)制造后处理(减材加工)过程中结构的加工稳定性与热处理工艺成品率保证。

借助增材制造技术在复杂构型制造方面的灵活性优势，综合应用结构构型优化设计方法，提出一种面向增材制造技术的桁架式支架结构设计流程，首先，在结构可行设计空间中，通过拓扑优化方法寻找给定载荷与边界条件下的结构主要承载路径，在此期间结合增材制造工艺约束对拓扑优化模型进行反复调整(调整内容包括可行设计空间尺寸、结构最大特征和最小特征尺寸以及模型边界条件等)，直至获得工艺可行的概念构型方案；其次，将初步构型抽象形成桁架形式的结构，应用尺寸优化确定桁架各杆件最优截面尺寸，形成结构基本构型方案；最后，基于尺寸优化结果，兼顾结构安装、使用约束，进行几何重构，获得光顺化的、可用于增材制造的结构详细设计方案。完整流程如图1所示。

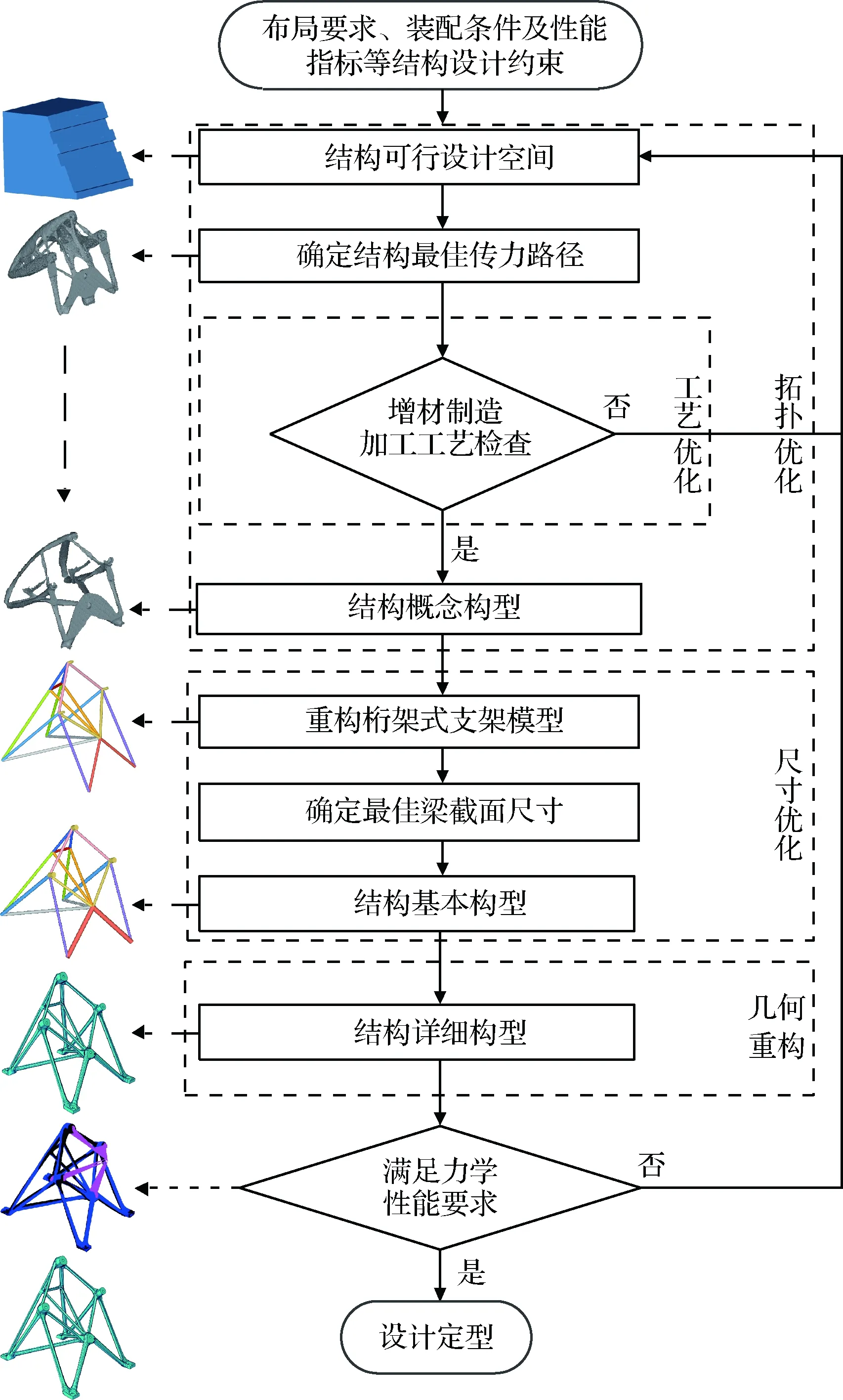
图1 桁架式结构设计流程Fig.1 Design process of trussed structure

在静力学范畴，结构优化方法建模思路一般有两种：一是在体积或质量约束条件下寻求结构刚度最大化(最小柔度)；二是在刚度约束条件下寻求结构最小体积或质量。

流程中拓扑优化主要用于确定结构中的承载路径，可归类于第一种结构优化问题。该问题的数学模型可抽象为：以支架结构可行设计空间内单元相对密度为设计变量，以设定的结构体积分数为约束条件，考虑结构最大最小尺寸、对称等加工制造约束，实现结构在给定的载荷和边界条件下刚度最大化。与之对应的基于变密度法固体同性惩罚微结构模型(Solid isotropic microstructures with penalization, SIMP)理论的数学模型可描述为：

(1)

式中：x为设计变量，xe为单元设计变量；C(x)为结构柔度，N为单元数量，P为惩罚因子，ue为单元位移矩阵，ke为单元刚度矩阵；KU=F为结构平衡方程，K为结构整体刚度矩阵，U为结构位移矩阵，F为结构所受载荷矢量；V为设计变量状态下的结构有效体积，V0是设计变量取1状态下的结构有效体积，f为材料用量的百分比(体积分数)；Gk(x)-G*≤0表示最大最小特征尺寸约束；xmin和xmax是设计变量取值上下限，引入xmin是防止单元刚度矩阵奇异[5]。

流程中尺寸优化主要是在满足结构刚度约束条件下实现结构重量最轻化，属于第二种结构优化问题。该问题的数学模型可抽象为：在给定边界条件下，以桁架式支架结构中各个杆截面尺寸为设计变量，以设定的组合体模态频率为约束条件，实现结构重量最小化。与之对应的数学模型可描述为：

(2)

式中：x为设计变量，取值范围为[xlb,xub]；m(x)为结构重量,Q*-Qs(x)≤0为模态频率约束条件。

2 某敏感器支架结构设计

支架设计用于安装某型号敏感器。敏感器底部安装面提供了4个安装孔。支架作为敏感器的承力部件，设计应满足：1)功能要求，如提供稳定的安装界面以保证敏感器的工作指向；2)性能要求，如支架(在安装敏感器的情况下)能够抵抗运载发射环境而不发生有害变形；3)装配环境适应性要求，如支架布局满足总体要求；4)轻量化要求，新型支架减重目标是传统构型支架重量的30%。

2.1 概念构型设计

根据设计要求，确定支架可行的包络空间—一种截面为直角梯形的空间结构，如图2所示，该结构体积小于铺粉制造工艺可加工的最大尺寸。其中A面为敏感器安装面，表面凹槽为适应设备安装设计的，B面为支架固定界面。对包络空间进行建立三维实体有限元模型，以集中质量单元模拟敏感器，置于敏感器质心位置，并通过刚性单元连接至支架，支架底部初步设计六个点固支约束，将敏感器上的过载以集中力的形式施加至其质心处，如图2所示。

拓扑优化设计数学模型为：1)设计变量为可行设计空间的单元虚拟密度；2)约束条件为设计空间体积分数小于10%，最小特征尺寸大于5 mm，最大特征尺寸小于25 mm；3)优化目标为静力工况条件下支架柔度最小。

基于已建立的有限元模型应用OptiStruct软件开展拓扑优化迭代。通过调整优化数学模型中的体积分数和结构基频约束，并在已有优化结果(见图3(a))基础上进行二次优化，最终得到如图3(b)所示的结构骨架。可以看出，敏感器载荷由4个安装点传递至支架，经由一定路径，并通过5个承载点传递至支架安装界面，支架中传力路径的材料聚集程度体现了各个路径的承载程度。除圆圈所示特征外，支架其它区域传力特征均至少由两条路径交汇而成。考虑到支架安装面精度要求以及在减材加工阶段因去除辅助支撑引起的局部变形可能性，决定舍弃该传力路径，调整图3(a)的模型边界条件如图3(c)所示，采用4点支撑的模型边界条件，最终经优化计算获得了图3(d)所示的支架概念构型，支架结构重量由27.6 kg减至约0.7 kg。

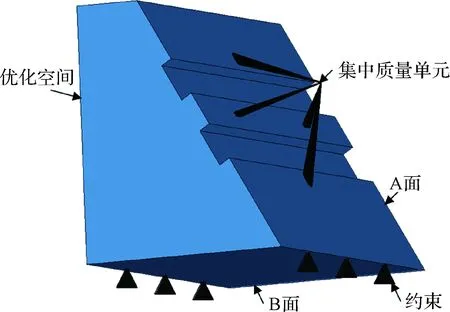
图2 概念优化设计模型示意图Fig.2 Conceptual model for the topology optimization

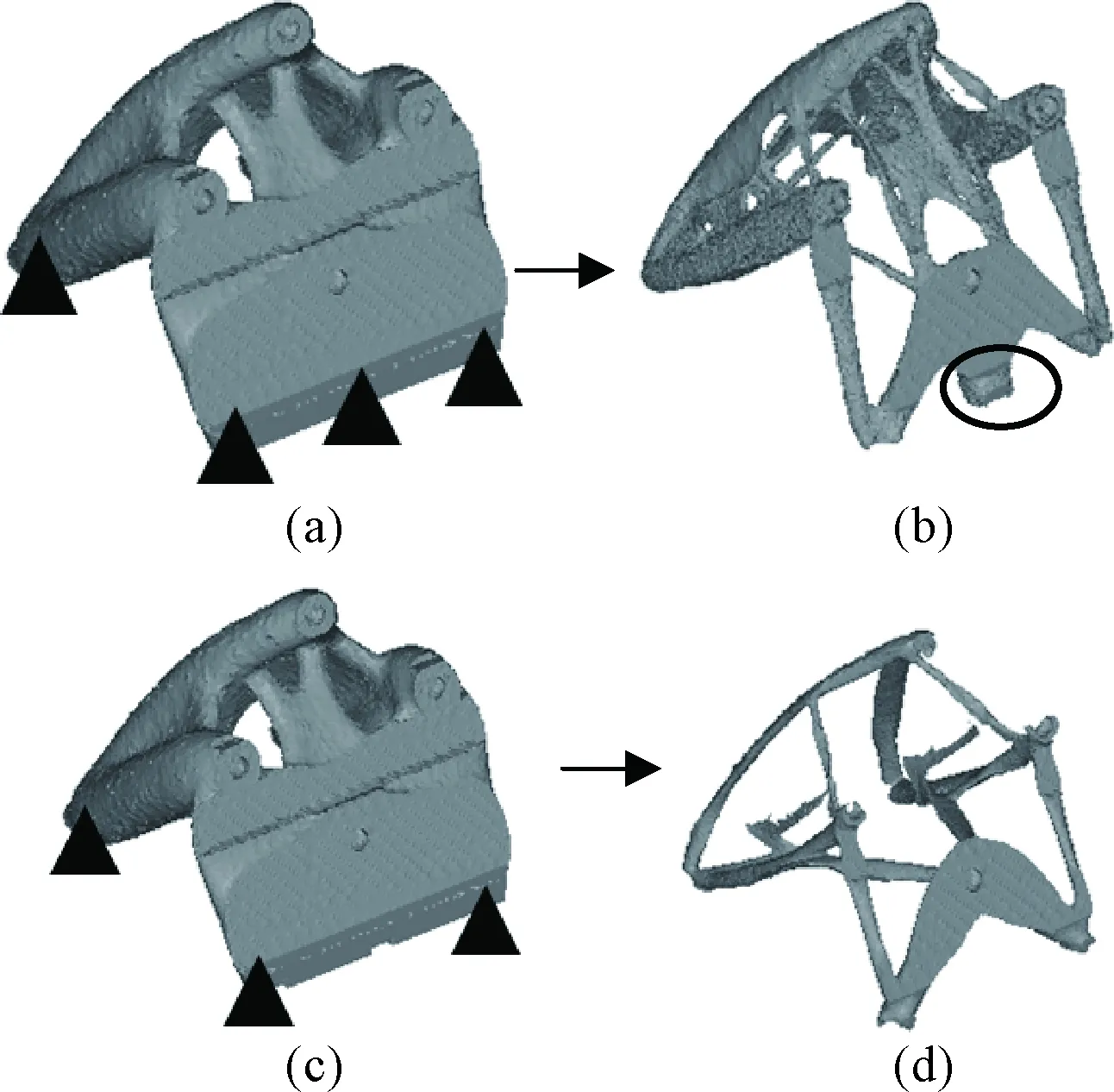
图3 支架概念构型Fig.3 The conceptual configuration of the bracket

2.2 基本构型设计

参考支架概念构型，基于“类桁架”结构设计策略并以实心圆杆件作为支架承载特征，将支架概念模型重建成一种由11种不同尺寸圆截面组成的桁架结构，如图4所示。

设计优化数学模型为：1)设计变量为杆件截面半径尺寸；2)约束条件为组合体一阶频率不低于280 Hz；3)优化目标为支架重量最小。

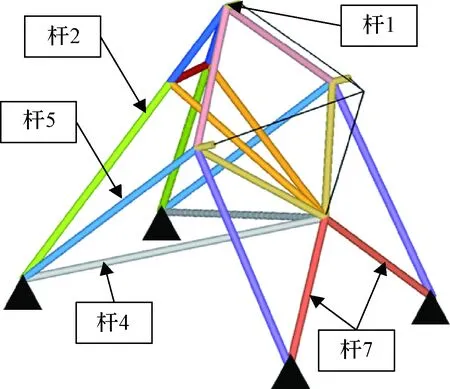
图4 桁架式支架结构示意图Fig.4 Trussed model for the size optimization

应用OptiStruct软件开展尺寸优化迭代。优化过程中目标函数与组合体基频迭代曲线分别如图5和图6所示，截面半径尺寸设计初值与优化结果如表1所示。优化后桁架结构重量由0.132 kg增加至0.199 kg，基频由为205.0 Hz上升到280.0 Hz。

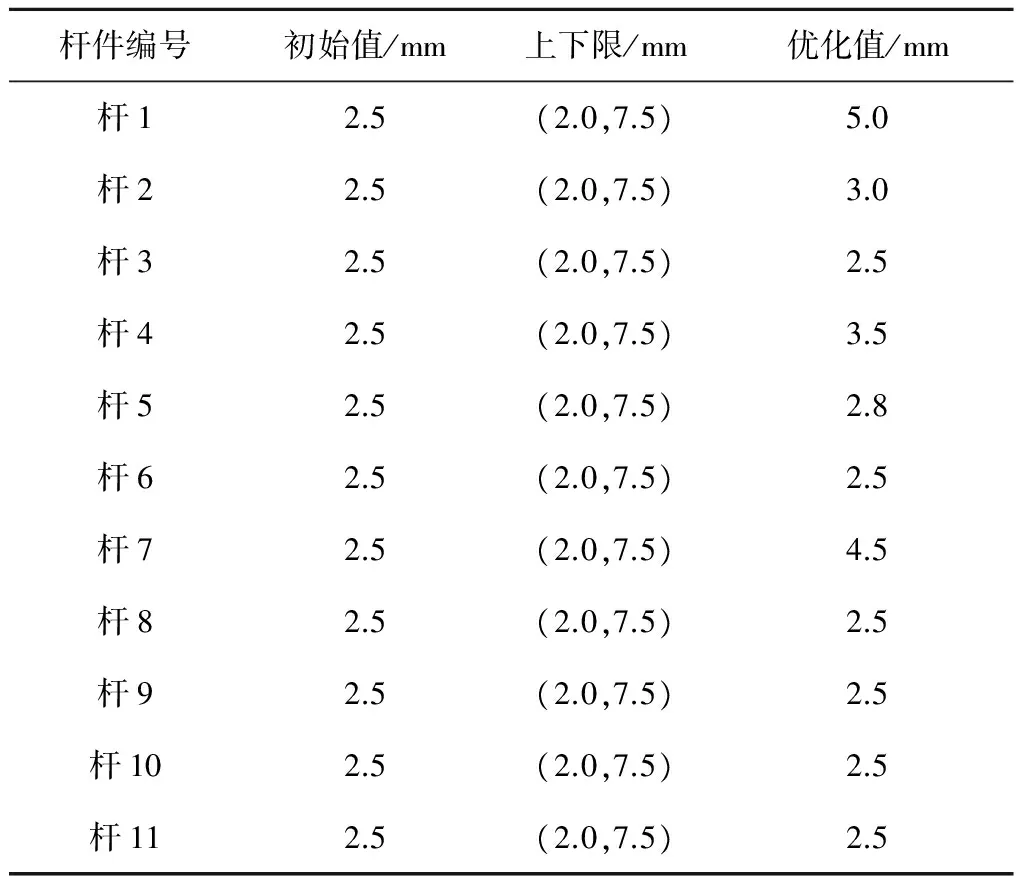
表1 杆件截面半径尺寸初值及最优值

由表1可知，支架中不同部位杆件承担载荷比例不同，截面尺寸上有所区别，其中杆1、2、4、5、7为主要传力路径，截面尺寸增加较多，其余杆件为次要传力路径，截面半径尺寸保持2.5 mm未变。得到支架基本构型如图7所示。

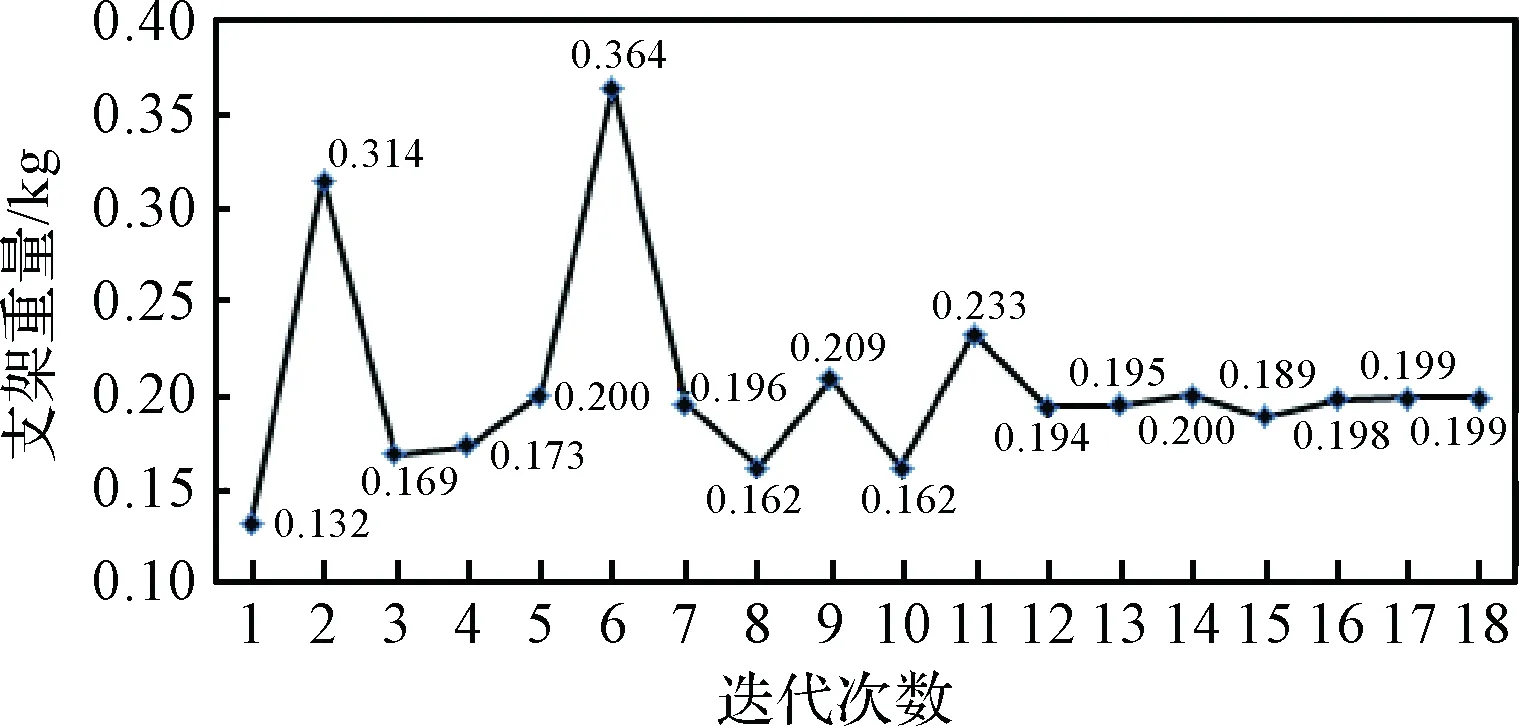
图5 支架重量迭代曲线Fig.5 Iterative curve of the weight of the bracket

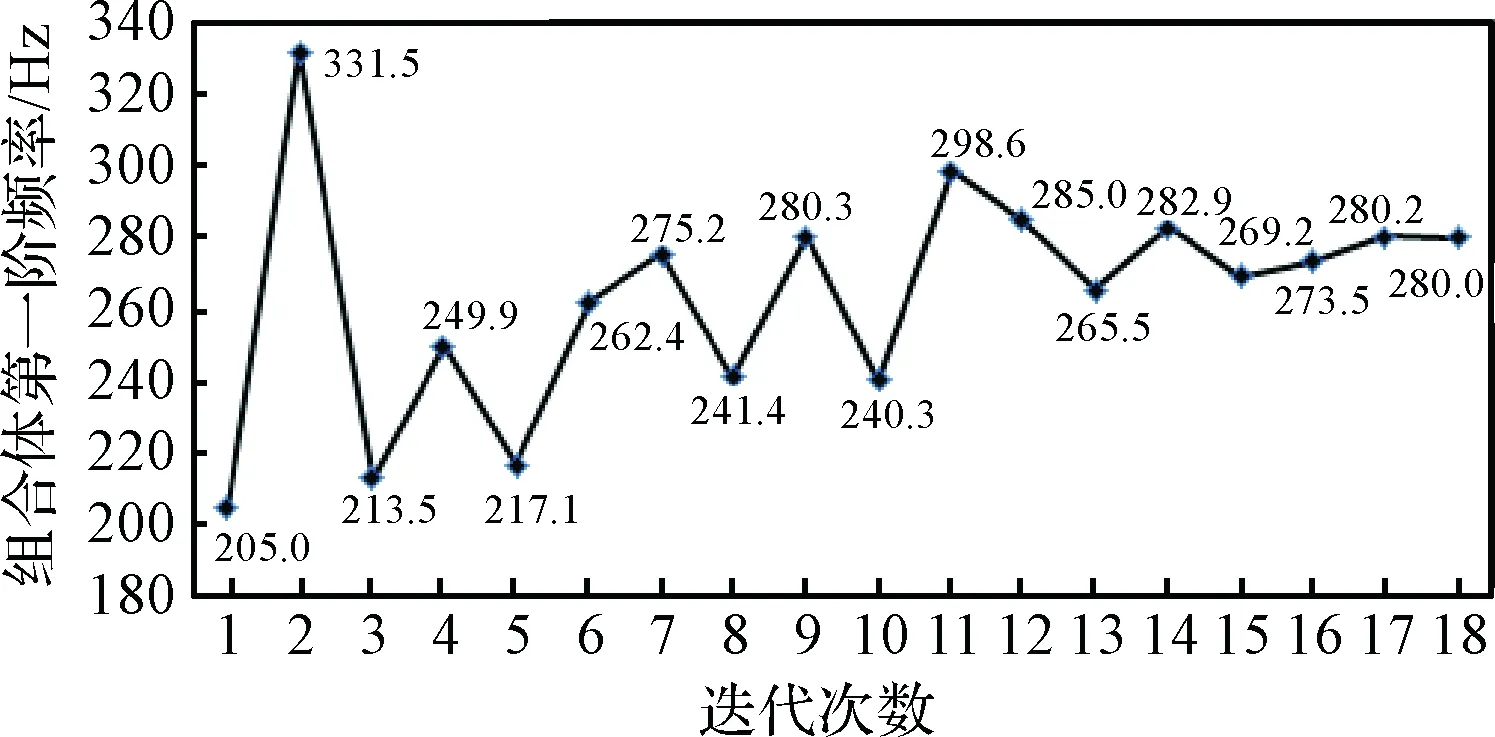
图6 组合体第一阶频率迭代曲线Fig.6 Iterative curve of the first mode of the combined structure

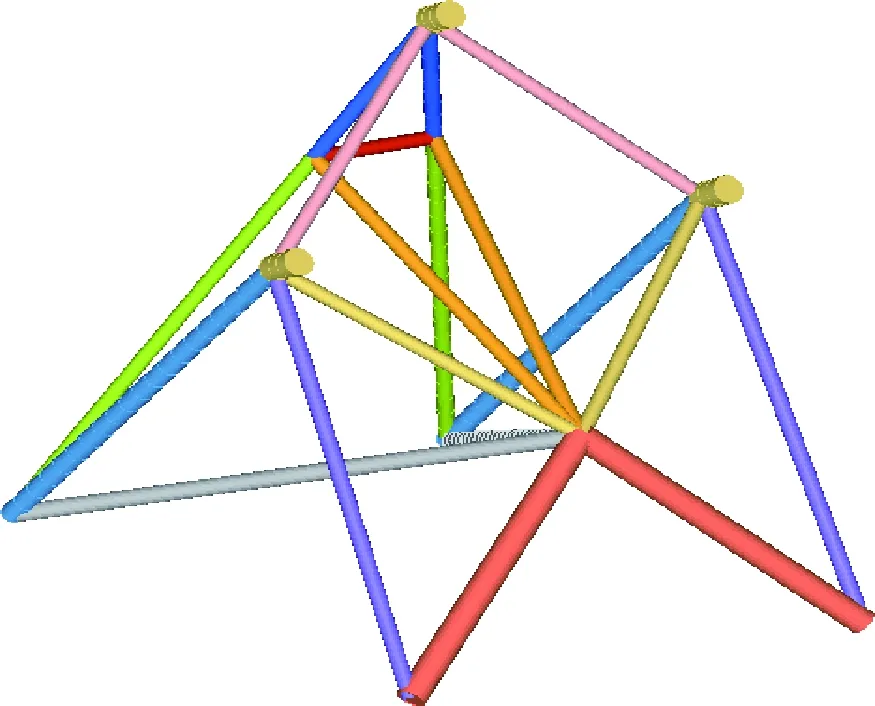
图7 支架基本构型示意图Fig.7 The basic configuration of the bracket

2.3 详细模型设计

应用Inspire软件在支架基本构型基础上进行支架重构建模，解决桁架各杆件接头区域的平滑过渡问题，然后应用CATIA软件完成支架功能性特征(如安装孔、安装平面等)的建模，最终获得图8所示的支架详细设计方案。指定支架为铝合金材料后，测得支架重约0.31 kg。

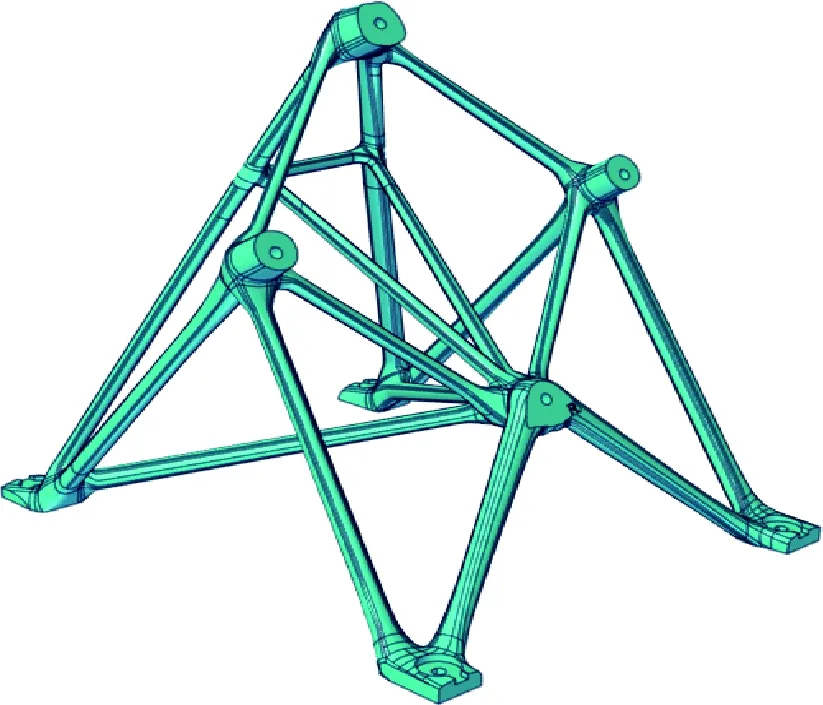
图8 支架详细设计构型示意图Fig.8 The detailed configuration of the bracket

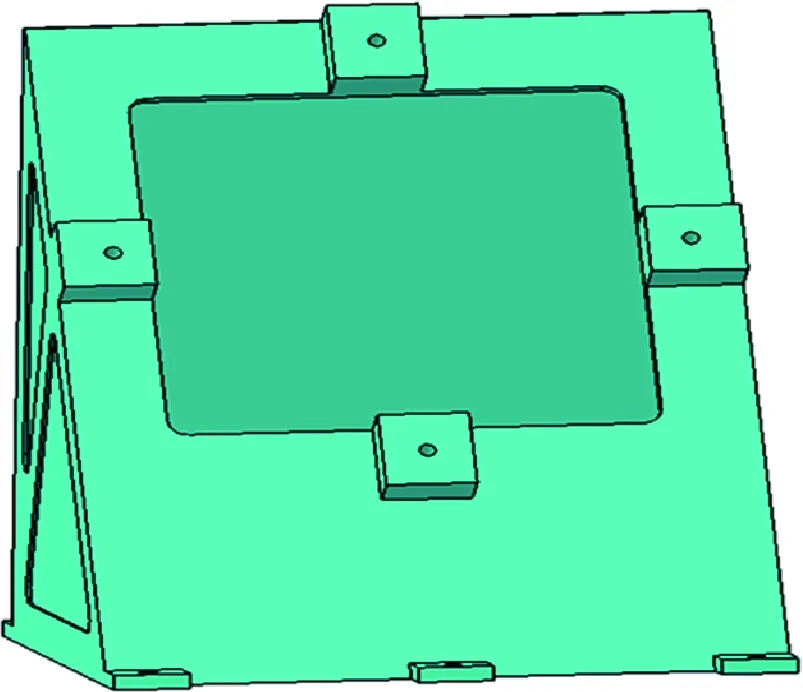
图9 支架原始(机加工)设计构型示意图Fig.9 The initial configuration of the bracket

3 仿真校验

进行支架力学分析，验证支架结构在静力、模态、频响、稳定性方面的性能。为便于比较，表2给出了支架原始(机加工)设计构型(如图9所示)相对应的性能。为对比验证支架构型对其力学性能的影响，力学分析时两种支架采用了相同材料参数，支架实际性能应以试验数据为准。图10给出了支架组合体第一阶模态振型，图11给出了x向载荷工况下屈曲变形云图。

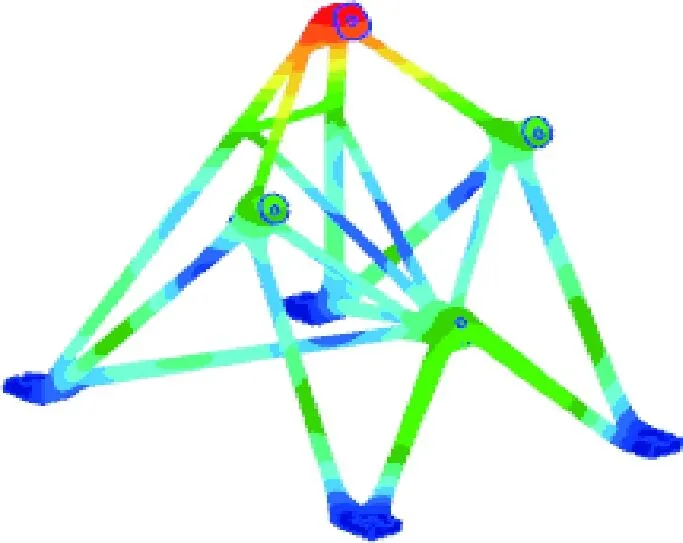
图10 支架组合体模态振型云图Fig.10 Mode shape of the combined structure

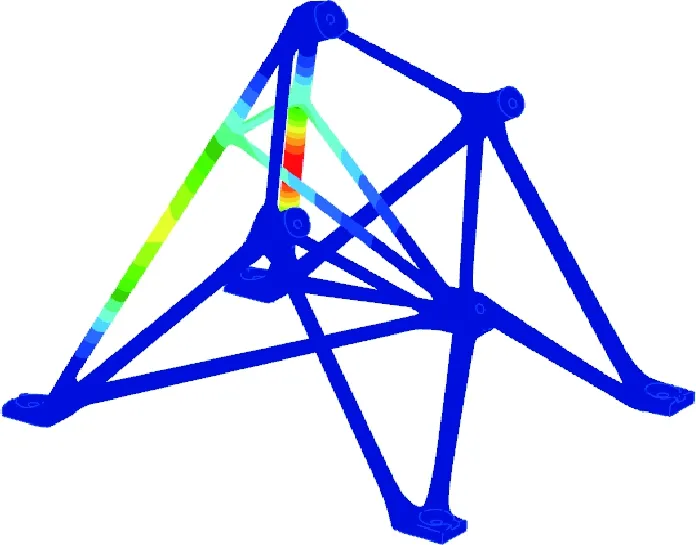
图11 x向载荷工况下支架屈曲变形云图Fig.11 Buckling shape of the bracket under the x direction load condition

项目新构型传统构型(相对传统构型)变化重量/kg0．310．4835．4%↓组合体前两阶模态/Hz279．6208．234．3%↑351．3299．617．3%↑结构最小安全裕度1．71．513．0%↑响应放大系数(0～500)Hz11．412．37．3%↓结构稳定性系数38．819．4100%↑

4 结 论

综合应用结构优化设计技术和增材制造技术，本文提出一种面向增材制造的桁架式支架结构轻量化设计方法。应用该方法设计了一种敏感器支架结构并完成支架力学性能对比分析。结果表明，相对于传统构型支架，新型支架重量降低35.4%，基频提高约34.3%，同时支架在强度、动态响应及稳定性方面均有不同程度提高，满足支架设计要求，验证了设计方法在工程应用上的可行性，为卫星结构轻量化设计提供一种新的解决途径。

目前新构型支架已进入试验件投产阶段，后续研究工作重点是面向实际工程应用的试验件力学性能试验验证以及根据试验数据进一步细化设计和完善设计方法。另外，该方法特别适用于安装接口简单的结构设计，如推广至具有复杂安装接口需求的结构设计时，在桁架结构重构设计及优化方面还需更进一步的研究。

[1] 张铁亮, 丁运亮, 金海波, 等. 航天器天线桁架结构多目标优化设计[J]. 固体力学学报, 2012, 33(6): 603-610. [Zhang Tie-liang, Ding Yun-liang, Jin Hai-bo, et al. Multi-objective optimization design for trusses of spacecraft antenna[J]. Chinese Journal of Solid Mechanics, 2012, 33(6): 603-610. ]

[2] 周志成. 通信卫星工程[M]. 北京: 中国宇航出版社, 2014: 253-306.

[3] 徐超, 李瑞杰, 游少雄. 卫星飞轮支架的共固化阻尼减振设计[J]. 宇航学报, 2010, 31(3): 907-911. [Xu Chao, Li Rui-jie, You Shao-xiong. Passive vibration control design with co-curing damping composite for a satellite flywheel bracket [J]. Journal of Astronautics, 2010, 31(3): 907-911. ]

[4] 范雪兵, 邓宗全, 高海波,等. 载人月球车金属弹性筛网轮设计与分析[J]. 宇航学报, 2014, 35(2): 235-244. [Fan Xue-bing, Deng Zong-quan, Gao Hai-bo, et al. Design & analysis of flexible wire mesh tire for manned lunar roving vehicle [J]. Journal of Astronautics, 2014, 35(2): 235-244.]

[5] 龙凯, 左正兴, 闫清东. 静动态多目标下的连续体结构拓扑优化[J]．宇航学报, 2008, 29(2): 456-460. [Long Kai, Zuo Zheng-xing, Yan Qing-dong．Static and dynamic multi-objective topological optimization of continuum structure[J]. Journal of Astronautics, 2008, 29(2): 456-460.]

[6] 郭中泽, 陈裕泽, 罗景润, 等. 旋转惯性过载作用下结构拓扑优化设计研究[J]. 宇航学报, 2007, 28(5): 135-136. [Guo Zhong-ze, Chen Yu-ze, Luo Jing-run, et al. Topology optimization of structure with rotary inertia loads[J]. Journal of Astronautics, 2007, 28(5): 135-136.]

[7] Zhou M, Rozvany G．On the validity of ESO type methods in topology optimization[J]．Structural and Multidiscipline Optimization, 2001, 21：80-83.

[8] 罗震, 陈立平, 黄玉盈, 等. 连续体结构的拓扑优化设计[J].力学进展, 2004, 34(4): 463-476. [Luo Zhen, Chen Li-ping, Huang Yu-ying, et al. Topological optimization design for continuum structures[J]. Advances in Mechanics, 2004, 34(4): 463-476. ]

[9] Thomas H, Zhou M, Schramm U. Issues of commercial optimization software development[J]. Struct. Multidisc. Optim., 2002, 23: 97-110.

[10] Krog L, Tucker A, Kemp M, et al. Topology optimization of aircraft wing box ribs[C]. The 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, New York, USA, August 30-September 1, 2004.

[11] 徐福祥. 卫星工程概论[M]. 北京: 中国宇航出版社, 2003: 76-81.

[12] 张学军, 唐思熠, 肇恒跃, 等. 3D打印技术研究现状和关键技术[J]. 材料工程, 2016, 44(2): 122-128. [Zhang Xue-jun, Tang Si-yi, Zhao Heng-yue, et al. Research status and key technologies of 3D printing[J]. Journal of Materials Engineering, 2016, 44(2): 122-128. ]

[13] 李怀学, 巩水利, 孙帆, 等. 金属零件激光增材制造技术的发展及应用[J]. 航空制造技术, 2012, 20: 26-31. [Li Huai-xue, Gong Shui-li, Sun Fan, et al. Development and application of laser additive manufacturing for metal component[J]. Aeronautical Manufacturing Technology, 2012, 20: 26-31. ]

[14] 郝宝新, 周志成, 曲广吉, 等. 大型航天器桁架式主承力结构构型拓扑优化研究[J]. 航天器工程, 2014, 23(2): 44-51. [Hao Bao-xin, Zhou Zhi-cheng, Qu Guang-ji, et al. Research on configuration topology optimization for main truss structure of large spacecraft[J]. Spacecraft Engineering, 2014, 23(2): 44-51.]

通信地址：北京市5142信箱318分箱(100094)

电话：(010)68117858

E-mail:lixiufeng_its@126.com

An Additive Manufacturing Oriented Structural Design Method for Trussed Bracket

LI Xiu-feng, GAO Ling-fei, WANG Wei, WANG Hao-pan

(Institute of Telecommunication Satellite, China Academy of Space Technology, Beijing 100094, China)

In order to satisfy the lightweight requirements of satellite structure, a structural design process which combines the advantage of the topology optimization method in structural design and the advantage of the additive manufacturing in structural manufacture is proposed in this paper. Firstly, the best load path is found in the feasible design space using the topology optimization method with the additive manufacturing constraints in mind. Secondly, a trussed structure is extracted from the optimized results and the cross-sectional dimension of the truss is optimized using the sizing optimization method. Finally, after rebuilding the structure based on the previous analysis results and some essential geometry features, a new additive manufacturing oriented design is obtained. Applying the proposed method to a sensor bracket of a satellite, a lightweight design whose mass is reduced by about 35.4% relative to the original design is achieved. With the same material parameters and load cases as the original design, the detailed mechanical analysis shows that the new design improves the fundamental frequency by 34.3%, increases the margin of safety by 13.0%, and reduces the dynamic response coefficient by 7.3%. The test case verifies the feasibility of the proposed method in structural design and a helpful reference is provided for the lightweight design of the similar structure.

Satellite; Bracket; Structural optimization; Additive manufacturing; Trussed structure

2017-01-11;

2017-05-03

V423

A

1000-1328(2017)07-0751-07

10.3873/j.issn.1000-1328.2017.07.000

李修峰(1987-)，男，博士，主要从事航天器结构设计。