立方星带芯磁力矩器多目标优化设计与实现
2017-08-11王圣允
白 博,周 军,王圣允
(西北工业大学精确制导与控制研究所,西安 710072)
立方星带芯磁力矩器多目标优化设计与实现
白 博,周 军,王圣允
(西北工业大学精确制导与控制研究所,西安 710072)
针对立方星体积与功耗存在限制的情况下,如何得到磁矩大而体积小、重量轻、功耗低的带芯磁力矩器这一问题,采用多目标优化的方法进行磁力矩器的设计。首先,按照圆柱型磁芯上缠绕多层漆包线的结构,分别推导了磁矩、功耗与磁芯尺寸、漆包线直径以及绕线匝数之间的数学模型。其次,根据磁矩与功耗的数学模型,在质量与体积均存在约束的情况下,采用遗传算法对磁力矩器进行多目标优化设计。再次,根据带芯磁力矩器的磁感应强度与磁矩之间的关系,设计了磁矩的测试方法。最终,将所设计的参数进行了具体实现。对磁力矩器的测试结果可以看出,所设计的磁力矩器不仅输出磁矩线性度高、剩磁小,而且满足立方星标准的要求。所设计的磁力矩器在多颗立方星上的成功应用表明了该设计方案的有效性。
立方星;磁力矩器;多目标优化
0 引 言
立方体卫星(CubeSat)的概念最早由加州理工大学San Luis Obispo教授和斯坦福大学Bob Twiggs教授共同提出并制定了立方星相关标准[1]。“1U”立方星是以一个边长10 cm的立方体作为一个标准单元。在此基础上,立方星可进行升级,增大为“2U”(20 cm×10 cm×10 cm)至“12U”(30 cm×20 cm×20 cm)的结构[2]。其设计理念是通过标准化设计,减少卫星的研发制造成本[3]。
其中,磁力矩器作为重要的卫星姿态控制执行机构,由于其结构轻便、成本低、功耗小等优势,在地磁场强度较强的近地轨道卫星上应用十分广泛[4-6]。根据是否含有磁介质,磁力矩器可分为带磁芯的磁力矩器[7]与空芯磁力矩器两大类[8]。图1显示了国内外成功运用于立方星上的磁力矩器。图1(a)为CubeSpace公司生产的带芯磁力矩器,它可以产生较大磁矩,然而三轴同时使用这种磁力矩器,将占用立方星较大的体积。图1(b)为Hyperion Technologies生产的带芯磁力矩器,它通过加粗其中一个轴的直径来弥补磁芯变短产生的力矩降低。空芯线圈也可以产生磁力矩。图1(c)为TUGSAT-1卫星上使用的磁力矩器,其缺点是产生的磁矩较小[9]。图1(d)为荷兰代尔夫特理工大学研制的Delfi-n3Xt立方星磁力矩器,它采用了两根带芯磁力矩器与一套空心磁力矩器[10]。

图1 立方星上使用的磁力矩器Fig.1 Magnetorquers used in CubeSat
而将磁力矩器应用于立方星上时,由于需要遵循立方星的标准,因此需要在一定尺寸与功耗的限制下进行磁力矩器的设计。冯乾等在文献[11]中,针对空芯磁力矩器给出了优化设计的方法,但并未对带磁芯的磁力矩器设计方法进行讨论。文献[12-13]虽然考虑了带磁芯磁力矩器的设计问题,但该文并未同时考虑磁矩与功耗存在的矛盾。本文将系统地考虑带磁芯磁力矩器的质量、功耗与磁矩等因素,使得在有限功耗和尺寸的情况下,能够获得最大的磁矩输出,从而能够更好地应用于体积与功耗都有限的立方星中。
本文首先建立了带磁芯磁力矩器的磁矩与功耗模型,并分析了各因素对磁力矩器设计的影响。在此基础上,以功耗与磁矩这样一对矛盾进行多目标优化。最后针对所设计的参数制作了实际的磁力矩器,并对实物进行了测试,验证了设计的可行性与有效性。
1 模型建立
1.1 磁矩模型
带磁芯的磁力矩器,一般是在圆柱型磁芯上缠绕漆包线制成的。由于卫星姿态控制要求磁力矩器在断电时剩余磁场较小,因此磁芯应当采用软磁材料。其具体构造如图2所示。图中r1与l分别为圆柱型磁芯的半径和长度,r2为在磁芯上绕制漆包线后磁力矩器的半径,rw为漆包线的半径,I为通过漆包线的电流,A为圆柱型磁芯的圆形横截面积。
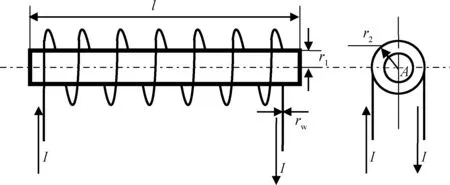
图2 带磁芯磁力矩器结构简图Fig.2 The structure of Magnetorquers with magnetic core
若假设漆包线是一个挨一个紧密排列在磁芯上,且当绕满磁芯一层后,漆包线仍可以在底层上再绕多层,每层之间的漆包线也是一个挨着一个紧密排列。当在磁芯上绕了n层漆包线后,所绕漆包线总的匝数N可由下式计算得出:
(1)
由于漆包线是密绕的,因此层数n可由r1、r2、rw计算得到,
(2)
考虑到绕在磁芯上第一层漆包线的一圈周长为2π(r1+2rw),紧挨着这一层上边第二层漆包线的一圈周长为2π(r1+2rw+2rw),依此类推,绕在最外边第n层漆包线的一圈周长为2π(r1+2nrw),同时考虑到每层都有N/n圈漆包线,则漆包线的总长Lw为:
2π(r1+2nrw)]=2πN[r1+(n+1)rw]
(3)
将以上线圈总匝数N与层数n分别代入式(3),可得到仅由l、r1、r2以及rw表示的漆包线总长Lw为:
(4)
若假设所绕漆包线的电阻率为ρ,则所绕漆包线的总电阻R为:
(5)
若假设在线圈两端所施加的电压为U,则通过漆包线的电流I为,
(6)
根据文献[14]的结论,磁芯所产生的磁矩M可由式(7)得出:
(7)
式中:k1为与磁芯材料有关的参数,具体形式为:
(8)
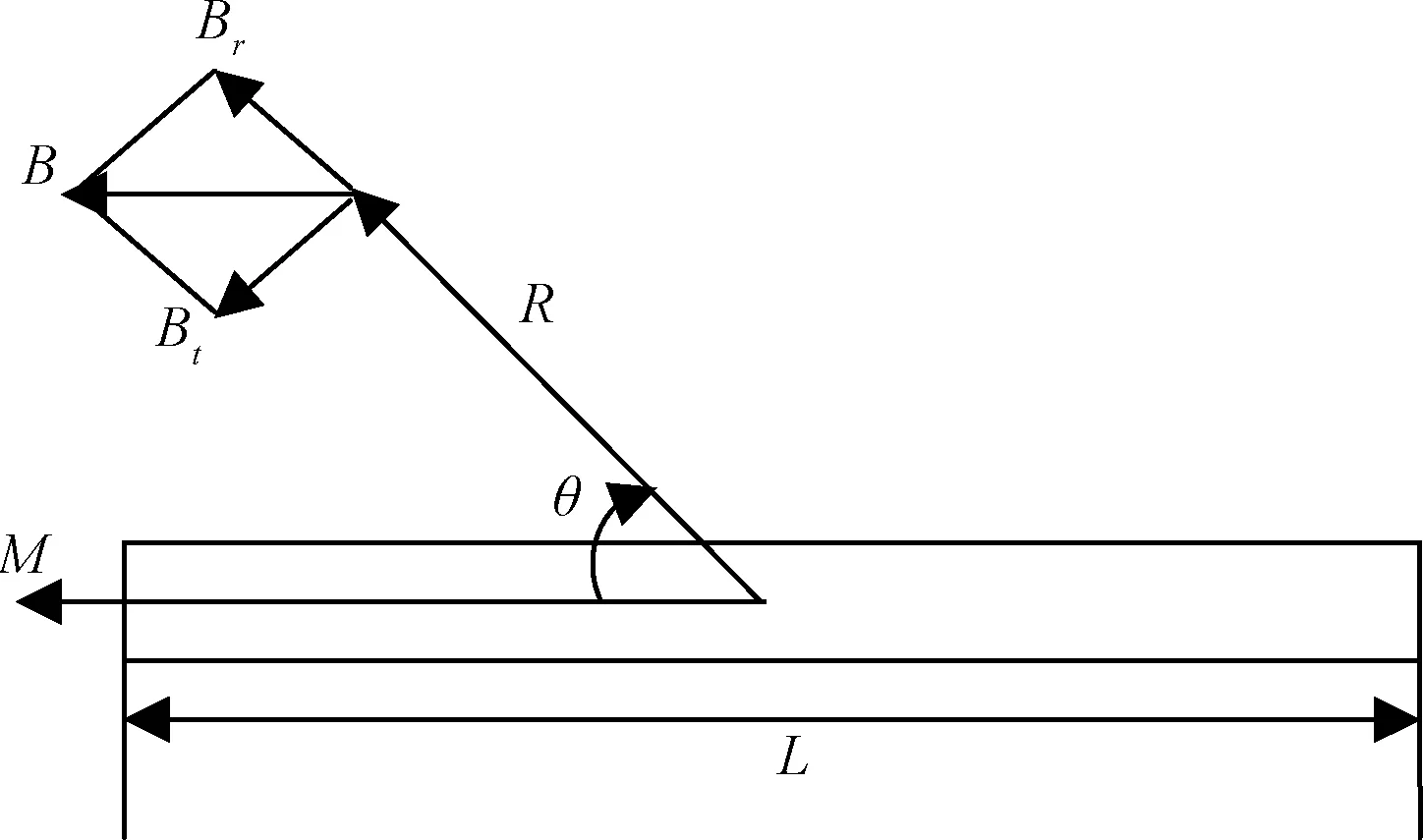
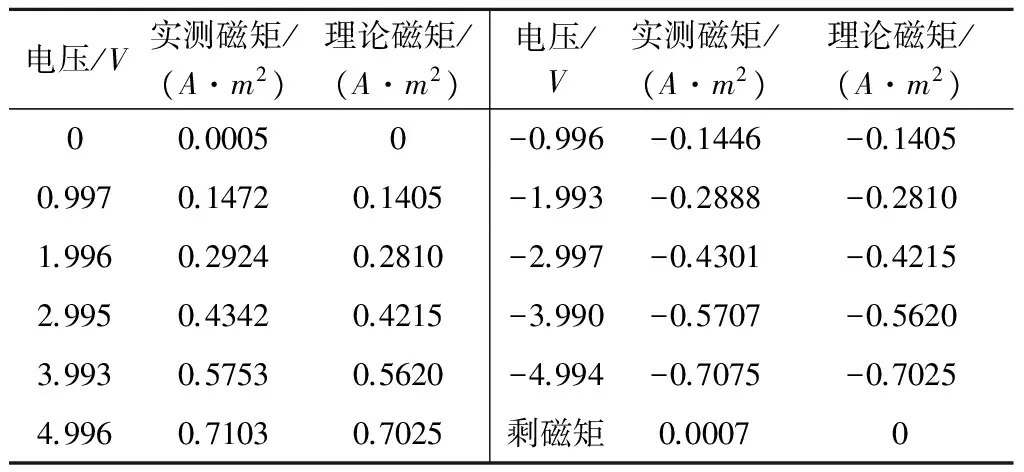
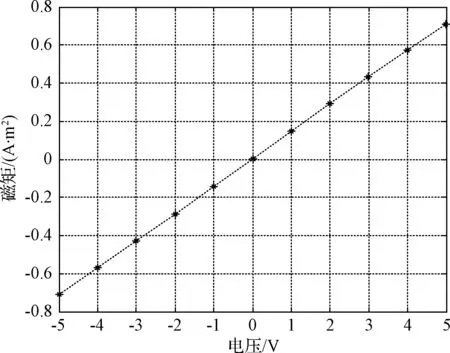
式中:μr为磁芯材料的相对磁导率。该公式只有在r1< (9) 经化简可得: (10) 由此可以看出,增大漆包线半径rw可以增大磁矩;而在电压一定的情况下,增大r2使得绕的线变多,从而导致电阻增大,电流减小,这反而使得磁芯可产生的磁矩减小。若假设采用rw=0.15mm的漆包线,以及固定的匝数N=4000 圈,则在U=5V的情况下,磁矩与磁芯材料的尺寸r1与l的关系见图3。 图3 磁矩随磁芯长度与半径的变化Fig.3 Variation of magnetic moment along the length and radius of the magnetic core 从图3可以看出,当磁芯半径r1一定时,磁芯长度l越长,磁矩就越大;当磁芯长度l一定时,磁芯半径r1的增加也会使得磁矩增大,但如果r1的增加破坏了r1< 由此可见,在电压一定的情况下,增大漆包线半径rw、增大磁芯长度l、减少匝数N(在磁芯半径r1一定的情况下,r2变小)、增大磁芯半径r1等措施都会增大磁矩。但对于体积和功耗都有限的立方星来说,增大磁矩意味着功耗的增加,因此,需要考虑影响功耗的因素。 1.2 功耗模型 由电压U与电阻R,可得功耗P, (11) 由式(11)可见,增大漆包线半径rw、减少匝数N(在磁芯半径r1一定的情况下,r2变小)、增大磁芯半径r1等措施虽然会使磁矩增大,同时也会使得功耗增加。因此要在立方星有限的体积和功耗限制下设计出磁矩较大的磁力矩器,需要综合考虑各量之间的平衡。 由以上分析可以看出,带芯磁力矩器在设计过程中,各个变量之间相互制约,单纯追求一个变量的最大化将导致其他变量恶化。因此,为了平衡各个变量,使磁力矩器整体达到最佳工作状态,需要对带芯的磁力矩器进行多目标优化。 选取磁芯长度l、磁芯半径r1、漆包线半径rw、绕线后磁力矩器半径r2这四个量为多目标优化的设计变量。用向量表示为: (12) 考虑到立方星1U空间的尺寸限制,按照边长为90mm的方式放置磁棒,同时考虑以下约束 0.002≤r1 (13) 0.00002≤rw≤0.0005,0.001≤l≤0.09 (14) 优化目标是使得磁矩M达最大,功耗P达最小。这样两个目标是相互矛盾的,需要同时对这两个物理量进行优化,因此选取如下的目标函数: (15) 采用遗传算法对目标函数进行最小化的寻优,经过250次迭代后,可得目标函数F(X)的变化情况如图4所示。由图4可知,遗传算法寻找的适应度F(X)最小值为0.8479,对应各参数为:l=0.09m、r1=0.0027m、rw=0.000112m、r2=0.005m。按照该参数计算可得磁力矩器输出磁矩M1=0.8825A·m2,功耗P1=0.5628W。 图4 适应度函数变化情况Fig.4 Variation of fitness function 3.1 线圈实现 由于所求得的导线半径rw=0.000112m这一最优值不符合工程实际中的导线规格,因此采用最接近的导线规格rw1=0.0001m。则最终磁力矩器实现的参数如下表所示,据此绕制完成的单根带芯磁力矩器如图5所示。 表1 磁力矩器实现参数 图5 绕制好的单根磁棒 3.2 驱动电路实现 考虑到模拟信号受磁棒线圈感性负载影响较大,因此驱动电路采用数字处理器的方式实现。这样,驱动电路与外界通过数字接口进行数据交互,减少了线圈对外界电路的影响。同时,由于采用了数字处理器,驱动电路可以完成电流采集、温度采集等功能。所设计的磁力矩器驱动电路框图如图6所示。 图6 磁力矩器电路设计整体方案Fig.6 The overall scheme of the magnetorquer circuit 其中处理器采用TI公司的MSP430F1611微控制器,该处理器为16位处理器、具有8MHz的工作频率、低至μA级的工作电流、内嵌12位ADC模块和SPI接口等特点。驱动电路采用TI公司的低压H桥集成芯片drv8837,该芯片专门用于驱动电机、步进电机或其他封装的绕组,最大可输出1.8A的驱动电流,适合1.8 ~11V的电机运行电源电压范围。最终集成的三轴磁力矩器如图7所示。 图7 磁力矩器实物图Fig.7 The photograph of the actual magnetorquer 由于缺乏直接测量磁矩的方法和手段,因而在测试中采用文献[14]方法,间接测量磁矩在空间中所产生的磁感应强度,然后通过磁感应强度反推出磁矩。 4.1 测试方案 测试的具体原理如图8所示。假设磁棒在距离其质心R处测得磁感应强度为B,同时Bt与Br分别是B沿径向和切向在坐标轴上的两个投影分量,则它们与磁棒的磁矩M满足式(16)~(17): 图8 磁矩的测量原理图Fig.8 The principle of the magnetic moment measurement (16) (17) 式中:μ0=4π×10-7N/A/A为真空中的磁导率,L为磁棒的长度,θ为向量R与磁矩M之间的夹角。为测量和计算方便,取θ=0°,式(16)~(17)可简化为: (18) Bt=0 (19) 因此,所测量的磁矩可表示为: (20) 由式(20)可知,磁矩的测量将转换为在确定位置的磁感应强度的测量。 4.2 测试结果 具体测量数据如表2~3所示。根据测量数据,电压与磁矩的关系见图9。 表2 磁力矩器磁矩测量数据 表3 磁力矩器功耗测量数据 图9 电压与磁矩的关系Fig.9 The relation between magnetic moment and voltage 由表2~3可以看出,所设计的磁力矩器在产生0.7103A·m2磁矩的同时,功耗仅为0.355W,且线性度误差小于1%。磁力矩器磁矩的实验结果和理论值的误差小于1.1%,剩磁矩小于1mA·m2。 本文所设计的磁力矩器已经在包括世界首颗12U立方星“翱翔之星”等多颗立方星上得到了应用。这些证明了设计方案的正确性和可行性。 通过本文的分析,可以得到如下结论: 1) 带芯磁力矩器所产生的磁矩不仅与所缠绕的漆包线直径有关,还与磁芯的几何尺寸有关。因此,在设计带芯磁力矩器时需要进行综合考虑。 2) 当需要满足立方星的标准时,磁矩与功耗是一对矛盾的物理量。需要采用多目标优化的方法进行设计。 最终从磁力矩器的具体实现和测试结果可以看出,本文所设计的磁力矩器质量轻、功耗小、剩磁小。这对于设计适合于立方星使用的磁力矩器提供了一些有益的参考。 [1]TwiggsR.Smallsatellites:past,present,andfuture[M].ElSegundo,California:TheAerospacePress, 2008. [2]FishCS,SwensonCM,CrowleyG,etal.Design,development,implementation,andon-orbitperformanceofthedynamicionospherecubeSatexperimentmission[J].SpaceScienceReviews, 2014, 181 (4): 61-120. [3] 于晓洲, 周军, 朱林妤. 低热层大气探测立方星翱翔一号轨道寿命分析[J]. 西北工业大学学报, 2013, 31(6): 896-900. [YuXiao-zhou,ZhouJun,ZhuLin-yu.LifetimeanalysisofChineseAoXiang-1Cubesatoflowerthermosphereresearch[J].JournalofNorthwesternPolytechnicalUniversity, 2013, 31(6): 896-900.] [4]SiJT,GaoY,AbadiC.Slewcontrolofprolatespinnersusingsinglemagnetorquer[J].JournalofGuidanceControlAndDynamics, 2016, 39 (3): 715-723. [5] 寇义民, 袁勤, 季艳波, 等. 一种基于几何分析的单轴指向磁控算法[J]. 宇航学报, 2017, 38(1): 65-71. [KouYi-min,YuanQin,JiYan-bo,etal.Ageometryapproachtosingleaxispointingcontrolusingonlyelectromagneticactuation[J].JournalofAstronautics, 2017, 38(1): 65-71.] [6]NobuoS,ToshinoriK,KuwaharaY.Attitudedeterminationandcontrolsystemfornadirpointingusingmagnetorquerandmagnetometer[C]. 2016IEEEAerospaceConference,BigSky,MT,USA,March5-12, 2016. [7] 肖琦, 张文彬, 孟立飞. 磁力矩器在磁洁净卫星平台中的应用技术研究[J]. 宇航学报, 2016, 37(2): 235-239. [XiaoQi,ZhangWen-bin,MengLi-fei.Researchonapplicationofmagnetorquerinmagneticcleanlinesssatelliteplatform[J].JournalofAstronautics, 2016, 37(2): 235-239.] [8]DegrandiRH,HeroeW,BudiS,etal.Designofattitudedeterminationandcontrolsystemusingmicrostripmagnetorquerfornanosatellite[C]. 2016InternationalConferenceonControl,Electronics,RenewableEnergyandCommunications(ICCEREC),Bandung,Indonesia,Sep13-15, 2016. [9]KoudelkaO,EggerG,JosseckB,etal.TUGSAT-1/BRITE-Austria-ThefirstAustriannanosatellite[J].ActaAstronautica, 2009, 64 (11): 1144-1149. [10]BouwmeesterJ,ReijneveldJ,HoevenaarsT,etal.DesignandverificationofaverycompactandversatileattitudedeterminationandcontrolsystemfortheDelfi-N3XTnanosatellite[C]. 2012SmallSatellitesSystemsandServices,Portoroz,Slovenia,June4-8, 2012. [11] 冯乾, 刘勇, 李立哲, 等. 纳卫星空芯磁力矩器的最优化设计与实现[C]. 第32届中国控制会议, 西安, 中国,2013年7月26-28日. [FengQian,LiuYong,Lili-zhe,etal.OptimaldesignandimplementationofcorelessmagnetictorqueforNano-satellites[C].Proceedingsofthe32ndChineseControlConference,Xi’an,China,July26-28, 2013.] [12] 孔庆松. 低轨小卫星高性能磁力矩器的设计与实现 [D]. 北京: 中国科学院研究生院, 2006. [KongQing-song.Designandimplementationofthehigh-performancemagnetictorquersforLowEarthOrbitsmallsatellites[D].Beijing:GraduateSchoolofChneseAcademyofSciences, 2006.] [13]ZhouML,QiHY.Designofthreeaxismagnetorquerformicrosatellites[C].The3rdInternationalConferenceonInstrumentation,Measurement,Computer,CommunicationandControl,Harbin,China,Sep. 21-23, 2013. [14]JamesL,NgA,JobanputraR.Ondeterminingdipolemomentsofamagnetictorquerrod-experimentsanddiscussion[J].CanadianAeronauticsandSpaceJournal, 2002, 48 (1): 61-67. 通信地址:陕西省西安市西北工业大学234信箱(710072) 电话:(029)88492787 E-mail:wuxian4683@nwpu.edu.cn Multi-Objective Optimization Design and Implementation of a Magnetorquer with Magnetic Core for Cubesat BAI Bo, ZHOU Jun, WANG Sheng-yun (Institute of Precision Guidance and Control, Northwestern Polytechnical University, Xi’an 710072, China) To solve the problem that how to design a large-magnetic moment, small-size, light-weight, low-power consumption magnetorquer with magnetic core under the constraint of the limited volume and power in a cubesat, a multi-objective optimization design method is used. Firstly, based on the structure of the cylindrical magnetic core with multiple layers of the enamel wires, the magnetic moment model and power consumption model are deduced from the magnetic core size, enamel wire diameter and turn number, respectively. Secondly, according to the model of the magnetic moment and power consumption, the multi-objective optimization design of the magnetorquer with genetic algorithm (GA) is used under the constraint of the limited mass and volume. Thirdly, based on the relation between the magnetic moment and the magnetic induction intensity, the measurement method of the magnetic moment is designed. Finally, the designed parameters are implemented. The test results show that the designed magnetorquer has the features of high linearity and low remanence, and it will satisfy the requirements of the CubeSat standards. The successful application of the designed magnetorquer in several CubeSats indicates the effectiveness of this design scheme. Cubesat; Magnetorquer; Multi-objective optimization 2017-04-13; 2017-05-04 航天支撑技术基金(2015-HT-XGD);西北工业大学基础研究基金(JC201205) V448.22 A 1000-1328(2017)07-0766-06 10.3873/j.issn.1000-1328.2017.07.000 白 博(1982-),男,讲师,主要从事微小卫星导航、制导与控制相关技术研究。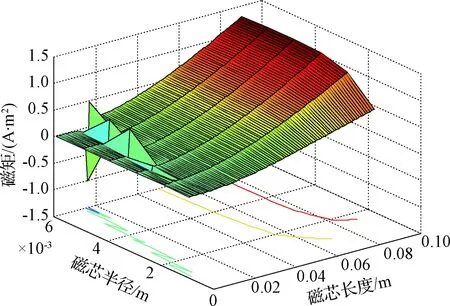
2 多目标优化
3 带磁芯磁力矩器的实现
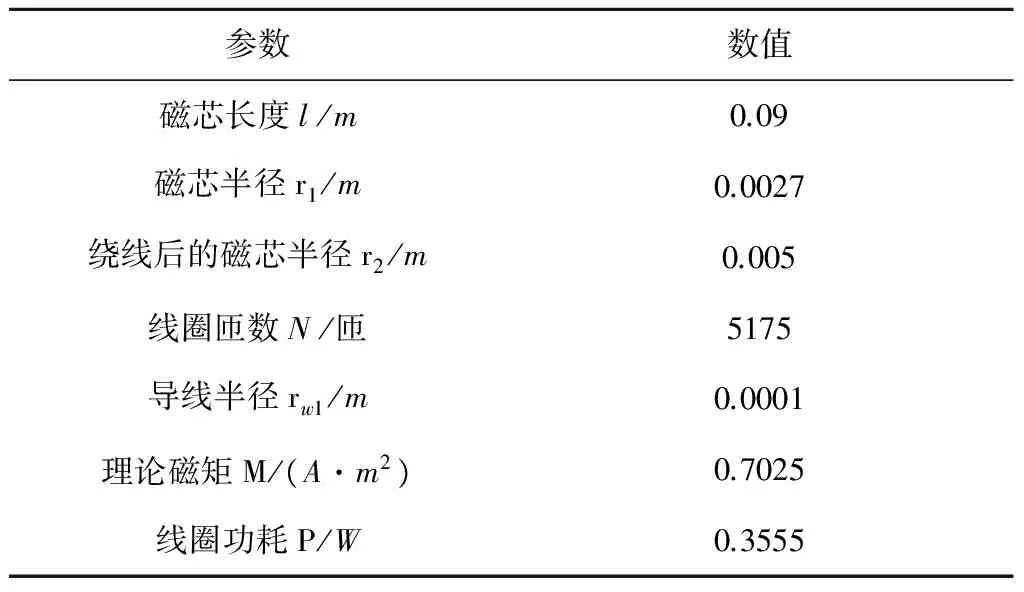

Fig.5 A single magnetic core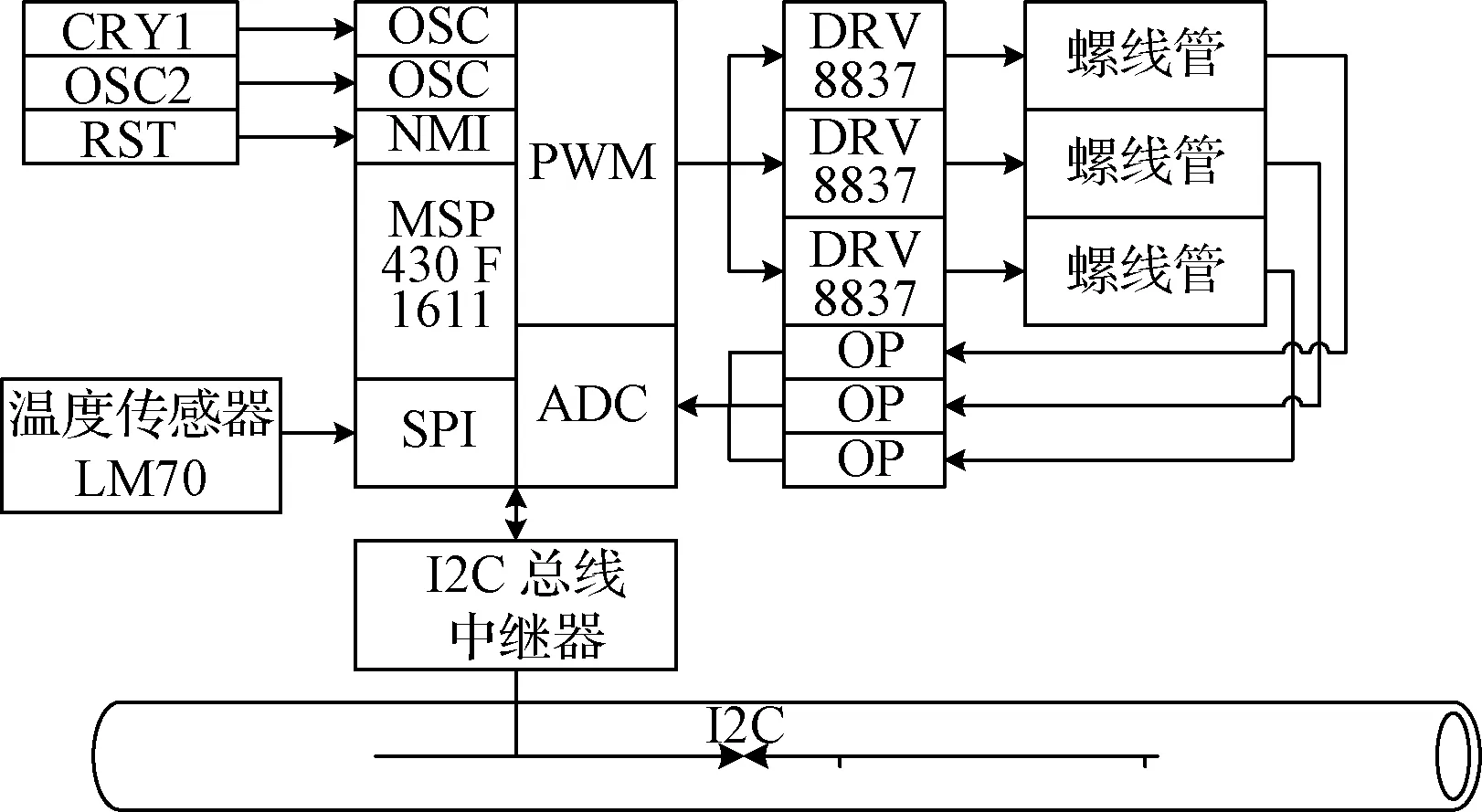

4 测试结果与分析
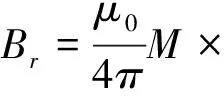

5 结 论
