反舰导弹靶场试验精度评定方法*

孙 锦，李国林，许 诚

（海军航空工程学院，山东 烟台 264001）

反舰导弹靶场试验精度评定方法*

孙 锦，李国林，许 诚

（海军航空工程学院，山东 烟台 264001）

为了对小子样条件下反舰导弹靶场试验精度作出合理的评定，研究了自助法和随机加权法的原理。针对自助法和随机加权法存在的不足，研究了一种改进的方法，仿真结果表明新方法获得了更加稳健、精确的评定。最后，给出一些有益的工程应用建议。

小子样，靶场试验，精度评定，自助法，随机加权法

引言

推断统计的目的是依据子样分布推测出对应总体的特征，即由子样的估计量推测出总体参数分布［1］。随着高科技的迅猛发展，逐渐形成一种模拟抽样统计推断的方法，自助法（Bootstrap）和随机加权法（Bayes Bootstrap）就属于这一范畴［2］。它的核心是用计算机对现有子样进行重新采样，得到新的仿真子样［3］。这两种方法仅仅依赖于给定的现场信息，不需要其他的假设和增加新的假设，为解决小子样试验评估问题提供了很好的思路，因此方法一经提出，便受到了统计界的重视［4］。本文将在研究自助法和随机加权法的基本原理和实施步骤的基础上，提出一种改进的自助法，为小子样条件下反舰导弹靶场试验精度评定提供一个新思路。

1 自助法原理

自助法是用重抽样方式获取新的子样，通过计算得出一系列估计值，再用一种“类比关系”就可进行统计推断，这种“类比”几乎是所有重抽样方式最核心的步骤。下页图1中左边表示传统的总体与子样间的关系，右边表示重抽样方法的子样与得到的新子样间的关系。将子样类比于总体，那么也就相当于知道了“真实”参数，将新子样类比于子样，也就可以求得诸如偏差、方差的估计值。通常这些估计都是采用多次重抽样之后的平均［5］。

图1 重抽样方法思想的示意图

2 随机加权法原理

随机加权法与自助法相仿，都是将子样信息“提携”以增加子样容量的方法。与自助法不同，随机加权法是用随机加权统计量Dn的分布去模拟Tn的分布。

3 改进自助法

无论是自助法，还是随机加权法，仿真产生服从经验分布的随机子样的取值区间仅局限在区间［x（1），x（n）］上，相对比较集中，其随机性就不能很好地满足统计学的要求；对于连续情况，两种方法都无法获得在非子样观测点处的分布特性，方法就可能失去其应有的意义。主要原因是子样的经验分布函数Fn拟合子样的上下限效果不好，以下用基于Bootstrap的一些其他函数修正拟合经验分布函数，获得改进自助法。

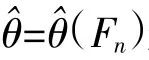
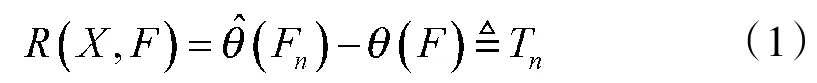
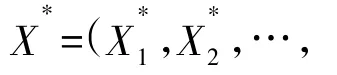
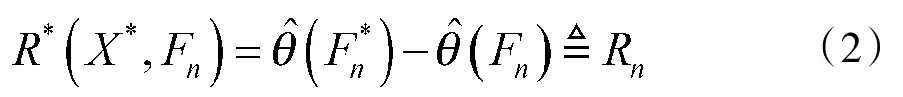
③重复循环步骤N次，计算N个Rn（j），j=1，2，…，N。

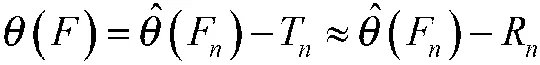
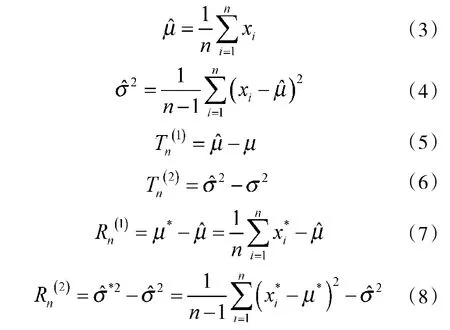
⑤产生N组D（1，1，…，1）的随机向量序列，V=（V（1），V（2），…，V（N））（1，1，…，1），j=1，2，…，N为每组V（j）的联合分布。则每组序列的因素可以如下产生：获取n-1个在［0，1］上均匀分布的独立子样u1，u2，…，un-1，按从小到大重新排列次序，记做u（1），u（2），…，u（n-1），设 u（0）=0，u（n）=1，令v（ij）=u（i）-u（i-1），i=1，2，…，n，则（v（1j），v（2j），K，v（nj））即为所求［8］；

⑥计算Dn（j），j=1，2，…，N；

⑦用Dn（j）的分布去模拟Tn的分布。即θ（F）=（Fn）-Tn≈ˆ（Fn）-Dn，可得未知参数θ（F）的N个可能取值，由此出发，作出未知参数的θ的统计推断［9］。

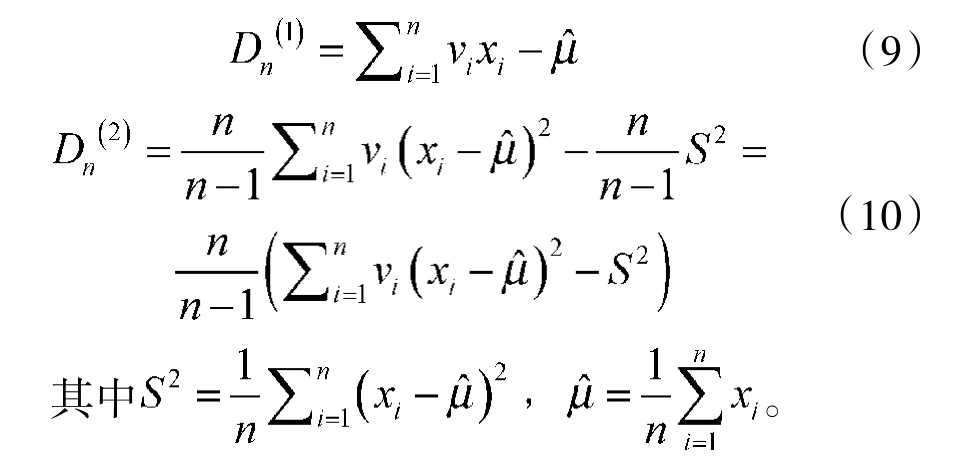
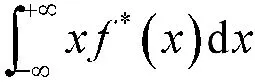
在得到修正子样分布函数F*（x）后，按照以下方法仿真产生新的随机子样：在［0，1］区间上产生随机数η（具有独立性和均匀性），x*=F*-1（η）就是所要的随机子样。

4 仿真分析

对总体分布已知的观测子样，进行参数估计，通过分析比较，证实改进自助法的合理性和有效性。

采用自助法和随机加权法估计参数μ的90%的置信区间，区间估计采样常用的百分位法。

分别由正态分布N（0，1）生成子样容量n为11、12、13的3组子样数据，见表1，分别作其经验分布函数，如图2所示。

表1 3组子样数据

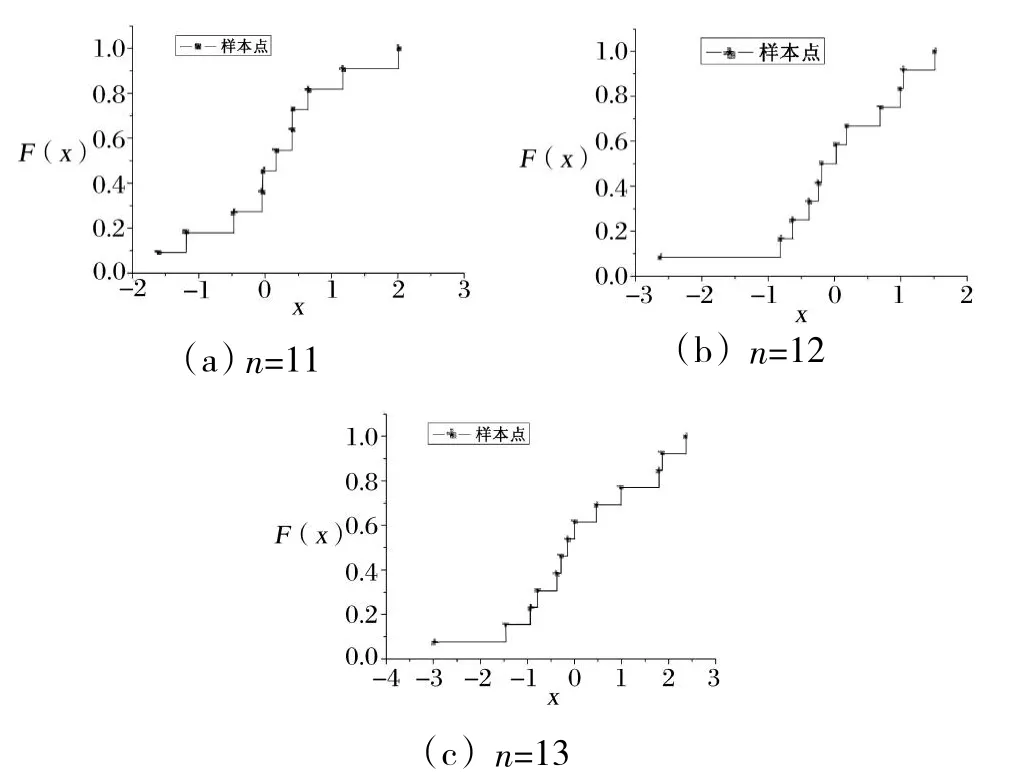
图2 经验分布函数

观察3组子样数据可发现所给子样的经验分布走向趋势近似于“S”形，再考虑到自助法和随机加权法的取值仅局限在区间［x（1），x（n）］上，所以考虑用Sigmoid类型的Boltzmann函数拟合子样经验分布函数。以下仅以n=11的子样数据为例进行分析，其他两组数据的分析方法与此相同。拟合结果如图3（a）所示。同理可以得出其他两组子样数据的拟合结果，见图3（b）、图3（c）。

图3 修正前后拟合的分布函数

依据拟合后分布函数产生N=10 000组统计量并做直方图，得到参数μ的分布如图4～图6所示，参数μ的估计值和区间估计见表2。

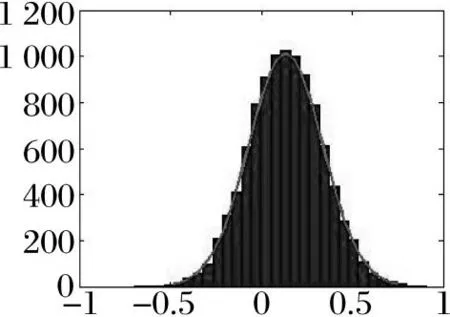
图4 改进的自助法

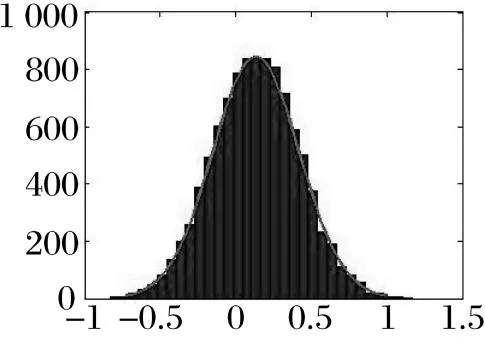
图5 自助法

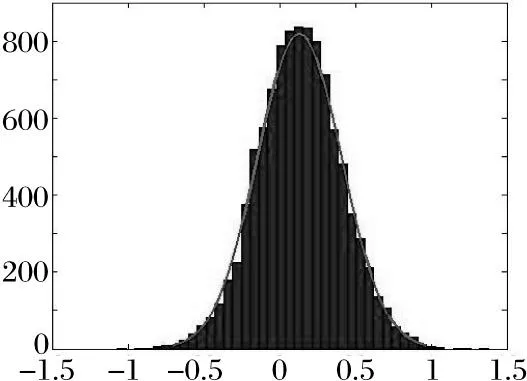
图6 随机加权法

表2 子样容量n=11的参数μ估计结果比较

通过仿真计算，可以明显看出仿真曲线都近似正态分布。下面将给出各种方法所求得μ的估计值和一个置信度为0.9的置信区间（用百分位方法）。为了说明以上方法的优越性，将采用经典统计法（方差未知的正态总体的均值估计）的估计结果也罗列出来，评估结果见表2。

同理可以得出其他两组子样数据关于参数μ的统计特性，见表3、表4。

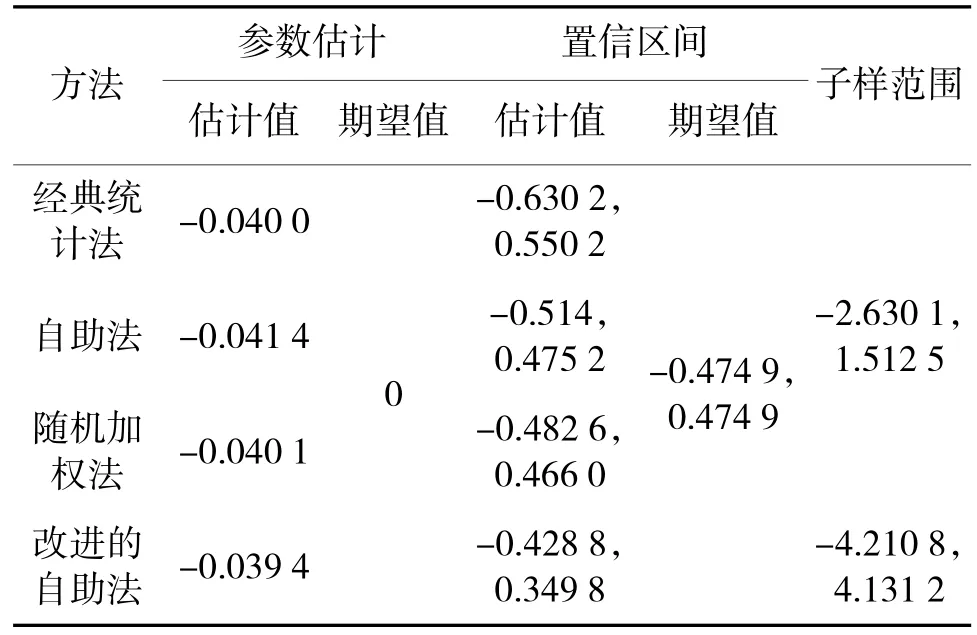
表3 子样容量n=12的参数μ估计结果比较

表4 子样容量n=13的参数μ估计结果比较

由图4～图6可以看出，随机加权法得出的直方图与自助法得出的直方图有一些差别。自助法的直方图显得较为光滑，这是因为自助法主要依赖于经验分布Fn（x），而随机加权法因为对原始数据和Dirichlet分布都比较依赖，所以其直方图表现的跳跃性较大、不光滑的特征，但其跨越区域也大，因此，对实际信息反映得更好。所以一般如果已知原始数据服从某一分布，宜用Bootstrap方法，而不能确定原始数据服从何种分布时则宜用随机加权法。

分析表2～表4中的仿真结果可知，在小子样数据条件下，用经典统计方法得到结论的估计误差比较大；采用自助法得到的参数精度有所提高，但不如随机加权法，随机加权法对参数μ的估计值最忠实于实际子样均值；改进自助法得出关于μ的估计值与真实值最为接近且置信区间精度最高。

随机加权法和自助法都将原子样点拓展至非观测点，所得精度有所提高，但这种提高是有限度的，原因在于上述两种方法所用子样最终仍局限在原子样的取值范围区间内。然而改进自助法使得子样可最大可能地拓展延伸，因而效果最好，精度最高。

对比表2～表4中区间估计的数据，还可以发现对同一种方法，随着样本量的增加，区间估计宽度却在增加，这是由于3组数据的方差值不断增大所致。

5 结束语

用自助法和随机加权法产生的随机子样存在取值范围受限的问题，该问题极易使得计算结果偏离真实分布过大，尤其在真实分布是连续分布的情况下，根本无法得到在非子样观测点处的分布特性，因而无法得到更接近于真实分布的分布估计。针对子样的经验分布近似于“S”形的情况下，采用改进的自助法，克服了以上不足，通过实例的仿真计算，获得了更加稳健、精确的估计，从而证实了方法是合理可行的。这也为小子样条件下反舰导弹靶场试验精度评定提供了一条新思路。

［1］Gosset W S.The Probable Error of a Mean［J］.Biometrika，2007（6）：1-25.

［2］Fisher R A.A Mathematical Examination of Methods of Determining the Accuracy of an Observation by the Mean Error，and by the Mean Square Error［J］.Monthly Notices of the Royal Astronomical Society，2008（80）：758-770.

［3］Miller R G.A Trustworthy Jackknife［J］.Annals of Mathematical Statistics，2009（39）：1598-1605.

［4］Efron B.Bootstrap Methods：Another Look at the Jackknife［J］.The Annuals of Statistics，2005：7（1）：1-26.

［5］肖支才，高华明，丁 通，等.自助法在小样本数据均值估计中的应用［J］.海军航空工程学院学报，2009，24（5）：563-572.

［6］Efron B，Tibshirani R J.Bootstrap Methods for Standard Errors，Confidence Interval，and Other Measures of Statistical Accuracy［J］.Statistical Science，2006（8）：54-77.

［7］Efron B，Tibshirani R J.An Introduction to the Bootstrap［M］. New York：Chapman&Hall，2002.

［8］Rubin D B.The Bayesian Bootstrap［J］.The Annals of Statisties 2003（9）：130-134.

［9］fron E F，B.Bootstrap Methods：Another Look at the Jack-Knife［J］.Annals of Statistics，2009（7）：1-26.

Research on the Method of Anti-ship Missile Accuracy evaluation in Range Trial

SUN Jin，LI Guo-lin，XU Cheng
（Naval Aeronautical and Astronautical University，Yantai 264001，China）

In order to evaluate the accuracy of small sample submarine launched anti-ship missile in range trial reasonably，Bootstrap method and Bayesian Bootstrap method are studied on their principle.At the same time，an improved method based on Bootstrap method is studied for the shortcomings of these two methods，the simulation result indicates that the new method gains the much more firm and accurate evaluation.At last，some profitable engineering applying suggestions are given.

small sample，range trial，accuracy evaluation，bootstrap method，bayesian bootstrap method

O212

A

1002-0640（2014）10-0095-04

2013-07-05

2013-09-27

国家部委重点资助项目（2010214019）

孙 锦（1985- ），男，河南商丘人，在读博士研究生。研究方向：武器系统与运用工程。