时变时/频差对长时相关积累的影响分析及补偿策略

朱珍珍，刘 丽

(1. 盲信号处理重点实验室，成都 610041；2. 国防科技大学信息系统与管理学院，长沙 410073)



时变时/频差对长时相关积累的影响分析及补偿策略

朱珍珍1，刘 丽2

(1. 盲信号处理重点实验室，成都 610041；2. 国防科技大学信息系统与管理学院，长沙 410073)

针对同步双星定位系统中时/频差(TDOA)/(FDOA)时变引起长时相关积累增益损耗的问题，将上下行传播链路的相对运动均考虑在内，推导同步双星系统中时变时/频差条件下的信号模型；在此基础上，根据规则信号自相关函数与能谱密度之间的关系以及线性调频信号的频谱特性，分别定量分析时变时/频差对长时积累时/频差维相关峰值幅度损耗的影响；给出了时变时/频差补偿策略和实现步骤。实际数据处理结果表明，本文给出的补偿策略能够实现长时相关积累的能量聚焦，时变引起幅度损耗定量分析结论的有效性也得到验证。

同步双星定位系统；长时相关积累；相关峰值幅度损耗；时变时/频差补偿

0 引 言

同步双星上行信号辐射源定位系统通过对主星和邻星转发信号进行相关处理提取两者之间的时/频差参数，再联合地球表面方程建立定位方程组实现辐射源定位，定位精度主要取决于参数估计精度，参数估计精度取决于信号的均方根时宽、均方根带宽以及相关增益，而相关增益与积累时长成正比[1]。当短时积累无法达到参数估计精度要求的相关增益时，需要长时相关积累以提高检测性能，其实质是利用时间换取能量。此时由于目标与双星之间相对运动的影响，相关峰位置会随着积累时间的推移而发生偏移，即形成距离单元走动(时变时差)和多普勒单元走动(时变频差)[2]。这些因素会造成相关峰值包络的时频二维展宽及峰值幅度降低，从而带来相关积累损耗、降低检测性能，限制了相关积累时长，导致时/频差参数估计精度较低甚至无法有效估计，系统定位能力有限。对时变时/频差影响的分析和补偿，是无源定位技术中的瓶颈问题。

文献[3-5]研究了时变时差未补偿条件下相关处理的输出信噪比和时差估计精度，其中文献[3-4]假设时差随时间缓慢线性变化，文献[5]假设时差二次变化，定量给出了特定参数估计性能要求下对时变时差补偿的需求，但仅仅研究了时差未涉及时变频差。文献[2]研究了低轨微纳卫星无源定位场景频差线性变化未补偿条件下的频差估计精度衰减因子，推导了不补偿时变的最优积累时间。上述文献的理论分析均建立在目标辐射源信号为“零均值平稳随机过程”的假设下，而且仅考虑了单程传播链路的场景，也没有利用实际数据进行验证。对于时变补偿，文献[6-8]通过信号分段、段内匹配滤波、段间傅里叶变换以补偿速度和加速度的影响，从而实现被动雷达中的长时相关积累，文献[9-10]进一步提出了降低运算量的补偿方法，但这些方法都是针对特定应用场景下的接收信号模型设计的，分段依据也不明确，不具备普适性；文献[11-12]对多个短时相关校正时间和相位偏移之后再进行相干累加，适用于信噪比较高的场合，而且对补偿必要性和性能的分析有所欠缺。

本文首先从双星定位系统的完整信号传播链路出发，推导了包含上下行相对运动参数的时变接收信号模型。在此基础上，对两路长时数据进行快慢时间划分，推导分析了时变时差对长时积累时差维相关峰值幅度损耗的定量影响；同时，利用线性调频信号频谱特性，推导分析了时变频差对长时积累频差维相关峰值幅度损耗的定量影响；给出了时变时/频差补偿策略和实现步骤。最后利用实际采集数据对理论分析进行了验证。

1 时变信号模型

由于两颗卫星受到的摄动影响存在差异，在时刻1，双星分别位于主星位置1和邻星位置1，时刻2，双星分别位于主星位置2和邻星位置2(见图1)。两个时刻分别形成不同的双星上下行传播路径，以及不同的上下行径向速度，分别产生不同的时差和频差。

目标辐射源信号可表示为：

s(t)=a(t)ej2πf0t+jφ0

(1)

式中：a(t)为基带信号，f0为载波频率，φ0为初始相位。假设在观测时间内，在卫星与目标的径向方向的相对运动为匀加速直线运动，暂不考虑噪声，则主星接收的上行信号可写为

sv1(t)=a(t-τ0,u1+ξu1t+0.5ζu1t2)·

exp(j2πf0(t-τu1+ξu1t+0.5ζu1t2)+jφ0)

(2)

式中：τu1为0时刻上行链路传播延迟，ξu1为延迟随时间变化的速度，ζu1为延迟变化的加速度。

经过星上转发器变频fT1后，主星向下转发，传播时延可写为τd1-ξd1t-0.5ζd1t2，其中τd1为τu1时刻下行传播时延，ξd1为延迟变化的速度，ζd1为延迟变化的加速度。将下行时延代入式(2)，忽略t的三次和四次项，信号到达地面接收站的信号可写为

sm1(t)=a(t-τ1+ξ1t+0.5ζ1t2)·

(3)

ξ1=ξu1+ξd1+ξu1ξd1-ζu1τd1(1+ξd1)

ζ1=(1+ξu1)ζd1+ζu1(1+ξd1)2-ζu1τd1ζd1

接收机下变频器设置为f0-fT1，则待处理的主星转发基带接收信号可写为

s1(t)=a(t-τ1+ξ1t+0.5ζ1t2)·

(4)

邻星转发基带接收信号与之类似，下标换为2即可。

2 相对运动参数对相关积累的影响分析

在积累时间内时差和频差均恒定的假设前提下，直接对两路接收信号进行窄带相关处理，互模糊函数定义为[1]

(5)

式中:τ和f分别为时差和频差搜索变量，将式(4)代入式(5)并化简可得

exp(j2π(fd+λt-f)t)dt

(6)

式中：α=-(ξ1-ξ2)，β=-0.5(ζ1-ζ2)

τd为0时刻两路接收信号的传播时差，α、β分别为时差随时间线性变化和二次变化的系数，fd为0时刻两路接收信号的传播频差，λ为频差随时间线性变化的系数。

在时/频差恒定假设下，忽略式(6)中的时变项系数α、β、λ，当时/频差二维搜索同时满足τ=τd和f=fd时，相对延迟为0时两路包络完全匹配(互为共轭)，互模糊函数取到理论相关峰值。文献[13]给出了时/频差恒定假设需要满足的条件：

(7)

式中：B为信号带宽。对比式(6)中的包络时差项，即要求在积累时间T内，最大时差变化αT+βT2远小于1/B。于是，当定位几何条件(径向相对运动状况)和信号条件确定时，α、β和B确定，上述参数恒定假设就限制了相关积累时间T的大小。

但是，当需要进行长时间积累以获取足够相关增益时，在积累时长内使用固定的时差和频差，时变项会影响实际处理得到的互模糊函数最大值偏离理论峰值。下面分别对时差维和频差维的相关峰值幅度损耗进行定量分析。

2.1 未补偿条件下时差维相关峰值幅度损耗

为了定量分析时变时差带来的时差维峰值幅度损耗，考察相关峰值在时差维的切片，即频差已得到完全匹配(时变频差也得到补偿)时，则时差维的互模糊函数切片可写为

(8)

为了更直观地反映时差随时间的变化给相关积累带来的影响，借鉴直扩信号捕获[14]和射频探测[15]等领域运动补偿中的快慢时间划分概念，将积累时间区间[-T/2,T/2]等分为M段，如图2所示。

图2 长时相关积累的时间区间等分
Fig.2 Time period partition of long-time integration

图中，分段准则为每段区间[tm-1,tm](其中t0=-T/2，tM=T/2)内均满足时差恒定假设，即T/M满足式(7)。取tm时刻的时差作为区间[tm-1,tm]内的恒定时差，则式(8)可写为

(9)

式(9)求和运算内每段积分的物理意义为有限时长信号a(t),t∈[tm-1,tm]的自相关函数，根据规则信号的自相关函数与能谱密度(信号频谱的模值平方)之间的关系[16]，将时域计算转化为频域可得

(10)

其中,A(f)为待处理长时信号的频谱，假设其在带宽[-B/2,B/2]内频谱近似平坦，式(10)可化简为

(11)

(12)

根据图2所示分段原则，tm的值为

(13)

令n=(-M+2m)/(2M)，将αBT简记为q，βBT2简记为p，变量替换后，式(12)可写为

(14)

图3 频差匹配时，不同q下相关峰值幅度损耗Fig.3 Magnitude loss of different q with matched FDOA

通过数值运算，图3给出了频差匹配、时差仅有线性变化即p=0时，不同q值下的时差维归一化互模糊函数即相关损耗随(τ-τd)B变化的切片，由图3可知：

1)随着q值逐渐增大，峰值逐渐下降，峰值附近包络逐渐拓宽；

2)当q=1时，峰值损耗约为0.6dB；

3)当q=2.31时，峰值损耗达到3dB；

4)当q>2.8以后，开始出现双峰，会大大增加时差参数估计误差。

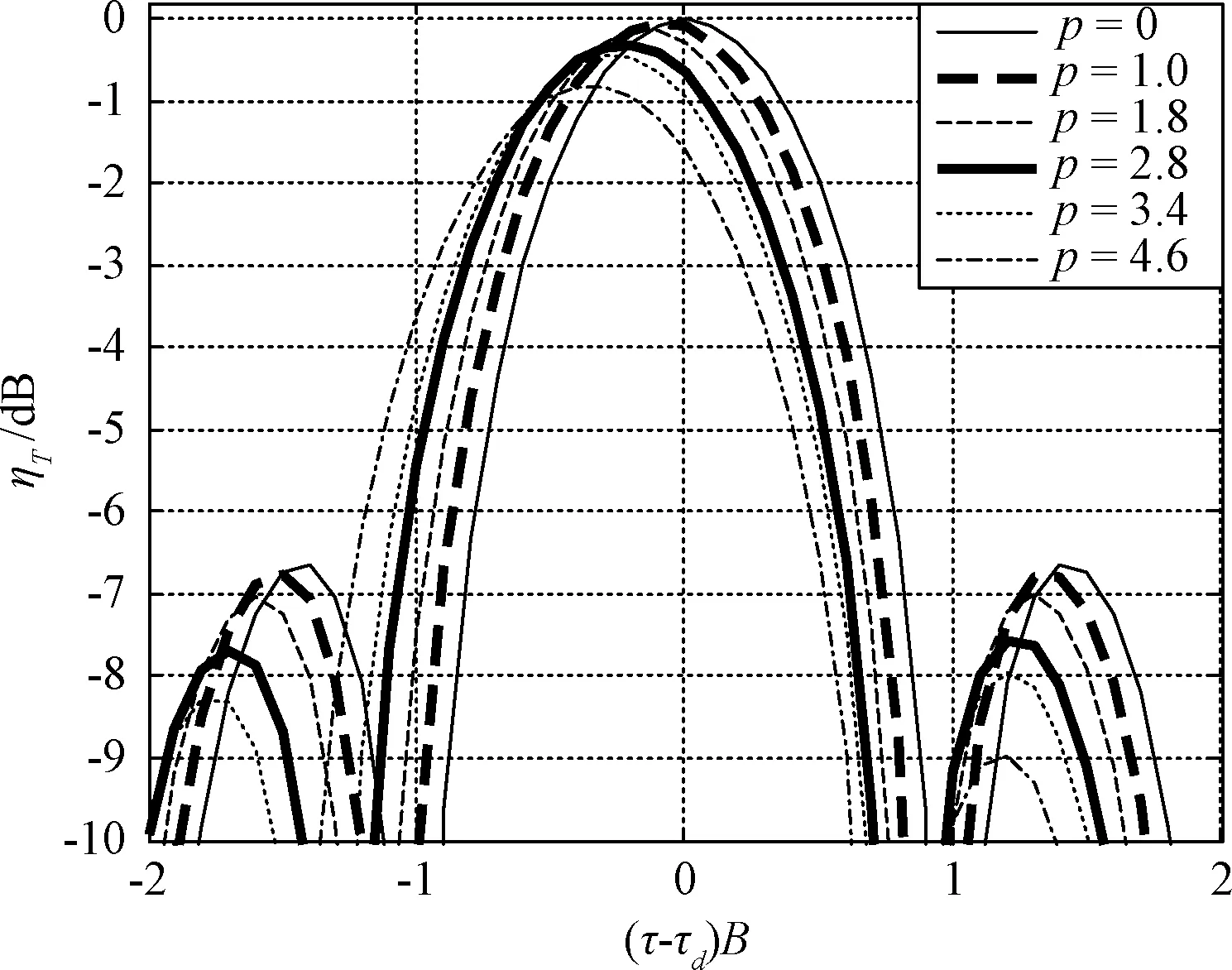
图4 频差匹配时，不同p下相关峰值幅度损耗Fig.4 Magnitude loss of different p with matched FDOA

由式(3)可知，α的主要数值部分为上行和下行路径的延迟随时间变化的速度，β的主要数值部分为上行和下行路径的延迟随时间变化的加速度，多数情况下，后者远小于前者。分析二次变化对损耗的影响时，不妨假设β为α的1/100，累积时长T取100s，此时p的数值与图3中的q相同，图4给出了频差匹配、时差仅有二次变化即q=0时，不同p值下的归一化互模糊函数即相关损耗随(τ-τd)B变化的切片。

对比图4和图3可以看出，与α项相比，β项的影响相对偏小，当仅补偿时差的线性变化而忽略二次变化时，可以挽回大部分时变损耗。

2.2 未补偿条件下频差维相关峰值幅度损耗

为了定量分析时变时差带来的时差维峰值幅度损耗，考察相关峰值在时差维的切片，即频差已得到完全匹配(时变频差也得到补偿)时，则时差维的互模糊函数切片可写为

(15)

(16)

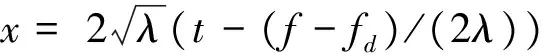
(17)

采用菲涅尔余弦积分和正弦积分公式

(18)

将式(18)代入式(17)，则频差维损耗因子可写为

(19)

(20)

从式(20)可以看出，频差维损耗因子仅取决于r和(f-fd)T，通过数值运算，给出了时差匹配时、不同r值下的频差维归一化互模糊函数即相关损耗随(f-fd)T变化的切片，从图5可以看出：

1)随着r值逐渐增大，峰值逐渐下降，峰值附近包络逐渐拓宽；

2)当r=3.072时，峰值损耗约为2.85dB，当r>3.072以后，开始出现双峰，会大大增加频差参数估计误差。

图5 时差匹配时，不同r下相关峰值幅度损耗Fig.5 Amplitude loss of different r with matched TDOA

3 时变时频差补偿策略

为了验证本文推导的时变引入损耗定量分析的有效性，利用实际双星转发的信号进行相关处理试验。第2节分析时差维和频差维时分别假设另一维度的参数及其时变性已得到完全匹配和补偿，所以本节给出时变时/频差的补偿策略。

图6为补偿实现流程图，各步骤说明如下：

1)首先尝试分成K段相邻等长的数据(每段长L点)求出各自时差，记录首段和末段的时差差异Δn(单位为采样点)，则经历(K-1)L点长的数据后时差变化了Δn。

2)取分段处理长度为(K-1)L/Δn，即时差变化1个采样点的数据点数，逐段进行补偿。

3)将当前分段数据(若时差绝对值逐渐变小，说明传播滞后的一路信号时延逐渐变小即信号在收缩，选择该路作为当前数据进行扩展；反之选择另一路)变换到频域，末尾补零，再变换回时域，则实现了时延扩展累积达到一个采样点的时域均匀调整，即时变时差的补偿。

4)此时得到时差已基本匹配的混合积信号，理想情况下是频率为频差的正弦信号，但频差是逐渐变化的，如式(15)积分所示，对第一段混合积搜索λ值，以相关增益最大为目标，完成该段频差时变补偿。

5)后续混合积搜索λ值，以与第一段频差差异最小为目标，以保证各段之间的相干累积。

图6 时变补偿流程图Fig.6 Flowchart of time varying compensation

完成全部数据的长时相干累积后，可以利用得到的时差和频差时变补偿参数，仅补偿时变频差以验证第2.1节关于时变时差影响的定量分析，仅补偿时变时差以验证第2.2节关于时变频差影响的定量分析。

4 实际数据验证

4.1 采集数据长时相关时变补偿

同步双星系统两路实际接收时变信号的采样率为3.125MHz，采集时长为32s，采样点数为100M。将长时数据进行分段，依据文献[17]的估计方法对各段进行相关处理，得到12段8M样点的时差粗估计和精估计如图7所示，以及12段频差粗估计和精估计如图8所示。

图7 未补偿时分段时差估计Fig.7 TDOA of every section without compensation

图7中纵轴单元网格长度为时差粗估计分辨率0.32μs，可以看出时差呈阶梯变化，每16M数据的时差减少1个粗分辨单元；时差精估计基本为一条斜线，说明时差近似为线性变化，也印证了第2.1节β数值远小于α的假设。

图8中纵轴单元网格长度为0.02Hz，而频差粗估计分辨率为0.3725Hz(每段处理时长的倒数)；从图8可以看出，12段8M样点的频差粗估计均为2053.38Hz；频差精估计基本为一条斜线，近似为线性变化，12段样点降低了约0.17Hz，变化率λ为0.0053Hz/s。虽然12段内频差变化没有超过一个粗估计分辨率(0.3725Hz)，但是，根据式(15)和式(16)，若不补偿该线性变化，频差搜索值取恒定值fd，则每个积分时间单元都离包络模平方有λt2的相位偏移。当时刻值为7s时(而12段样点总时长为32s)，相位约为π/2，在矢量图上对求和没有贡献，而且随着时间推移甚至带来负增长，所以频差的这种线性变化必然会引起长时相关积累的增益损失。

图8 未补偿时分段频差估计Fig.8 FDOA of every section without compensation

若不补偿时差频差时变，直接对64M样点的两路信号进行相关处理，得到未补偿时二维相关输出如图9所示(固定频差2053.38Hz已补偿)。图中峰值包络在时差维和频差维均有展宽，时差和频差的变化导致二维相关积累能量无法聚焦，而参数估计精度与相关峰尖锐程度成正比[16]；当信号信噪比较低、需处理更长数据以提高相关增益时，包络展宽很可能使有效相关输出被噪声淹没，无法完成信号检测。

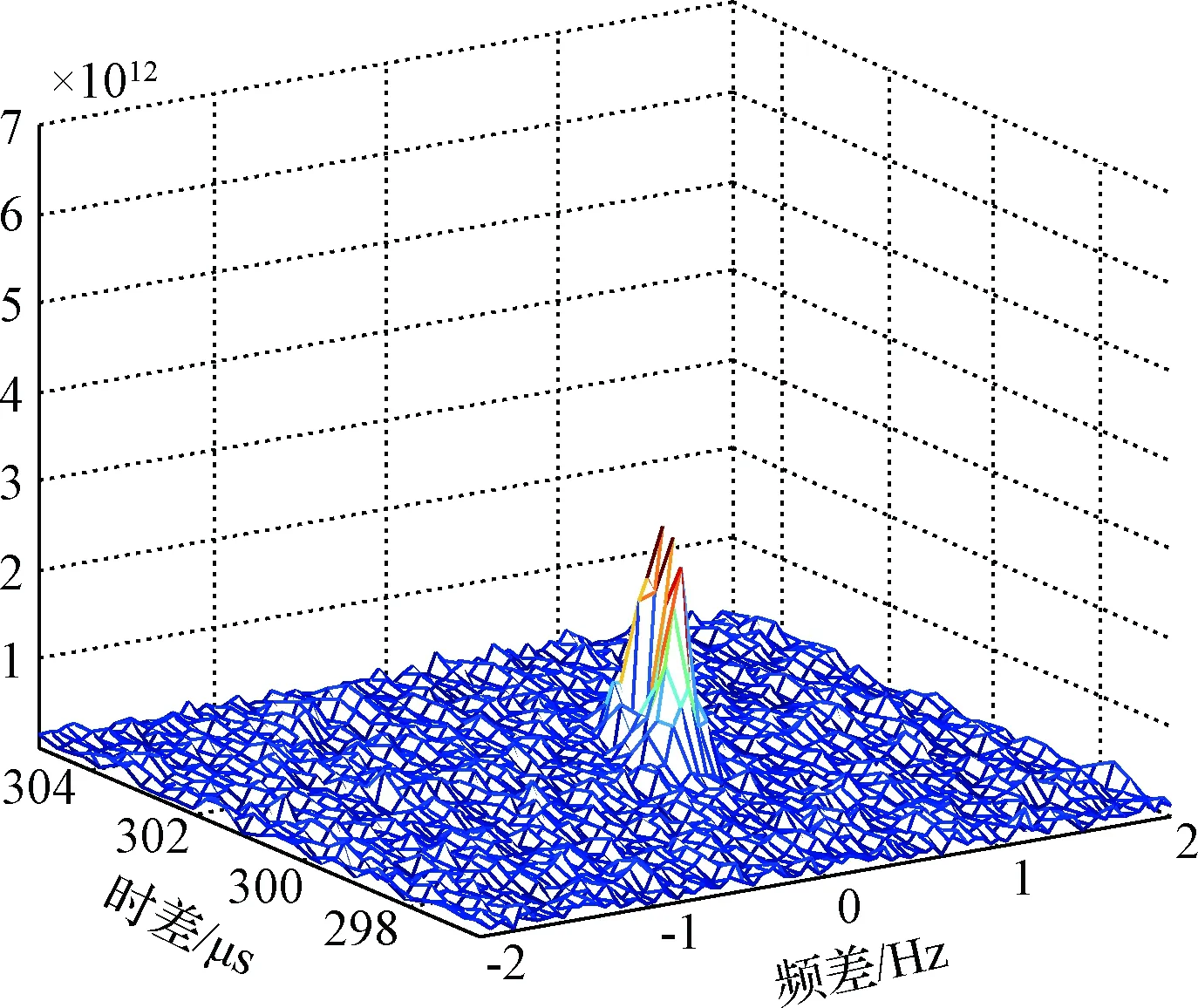
图9 长时数据直接处理二维相关输出Fig.9 CAF magnitude of long-time data without compensation

由未补偿时分段时差估计可知，每16M数据时差变化1个采样点，以该长度为分段补偿处理的段长。根据图6流程图逐段对64M数据进行时差和频差补偿以及相关处理，得到长时相关积累结果如图10所示。与图9相比，时差维和频差维的展宽均得到聚焦，峰值也大大提高，时变补偿使长时相关增益得以有效发挥。

图10 长时数据时变补偿后二维相关输出Fig.10 CAF magnitude of long-time data with compensation

4.2 长时相关二维时变对相关峰影响的验证

利用上述时差和频差时变补偿参数，分别验证前文推导的时变时差和频差影响的定量分析。

仅补偿时变频差，分别处理1M、16M、32M、48M和64M长度的数据，得到各自的归一化时差精估计相关曲线如图11所示。其中，后四种以1M长度相关峰值为基准进行归一化，16M样点时差偏移1个采样点，可近似认为1M样点内时差恒定。与图3各条曲线均关于横轴中心对称不同，图11曲线包络中心逐渐左移，原因是第2.1节增加时长(图3因变量为q、但实际信号αB已固定、故因变量等效为时长)的方式为由零时刻中心向两边对称加长，所以时差估计曲线的包络中心一致；而实际信号处理是由起始时刻逐渐加长，所以包络中心逐渐偏移。

从图11可以看出：

1)随着N逐渐增大，峰值逐渐下降，峰值附近包络逐渐拓宽，并且包络中心(即峰值位置)不断左移，这与图7的未补偿时差变化趋势是一致的，处理长度依次增加，平均时差依次减少。

2)当N=16M时，峰值损耗约为0.7dB，对应图3中q=αBT=1的情况，与后者相比损耗略高，是由于实际信号含噪声的影响，以及频差时变补偿存在误差的原因。

3)当N=32M时，峰值损耗约为3dB，对应图3中q=2.31的情况。

4)当N=48M时，峰值包络平坦，对应图3中q=2.8的情况，N=64M时已出现明显双峰，会大大增加时差参数估计误差。

图11 频差匹配时，不同处理长度N下相关峰值幅度损耗Fig.11 Magnitude loss of different N with matched FDOA

若要求的处理增益只需32M数据相关即可满足、且输入信号强度可以容忍3dB的相关峰值损耗，则不需进行时变补偿，反之则必须补偿。

图12 时差匹配时，不同处理长度N下相关峰值幅度损耗Fig.12 Magnitude loss of different N with matched TDOA

与时差维衰减验证类似，仅补偿时变时差，分别处理1M、48M和96M长度的数据，得到各自的归一化频差精估计相关曲线如图12所示，从图12可以看出：

1)随着N逐渐增大，峰值逐渐下降，峰值附近包络逐渐拓宽。

2)当N=64M时，峰值损耗约为2.7dB，时变补偿所得频差变化率λ约为0.005，则r=3.072对应时长21.7s，近似为64M处理长度，与图5结论基本吻合。

3)当N=96M时，出现三个较宽的峰值包络，大大增加频差参数估计误差。

5 结 论

本文建立了同步双星无源定位系统的完整链路时变信号模型，针对目标辐射源为规则信号的情形定量分析了时变时/频差对相关峰值幅度损耗的影响，与已有文献目标辐射源信号为“零均值平稳随机过程”的假设相比，更符合实际应用场景，给出时变补偿策略并用实际信号对所分析结论进行了验证。本文推导的定量结论解决了特定处理增益性能要求下、对时变时/频差参数补偿必要性和精确度需求如何的问题(即指标反推)，为同步双星系统可定位对象范围的拓展奠定了理论与试验基础。

[1]HaworthDP,SmithNG,BardelliR.InterferencelocalizationforEUTELSATsatellites-thefirstEuropeantransmitterlocationsystem[J].InternationalJournalofSatelliteCommunications, 1997, 15(3): 155-183.

[2] 李振强，黄振，陈曦，等. 时频差精度的时变性影响及补偿估计方法[J]. 系统工程与电子技术， 2016, 38(3): 481-486. [LiZhen-qiang，HuangZhen，ChenXi,etal.Effectoftime-varyingcharacteristicsonTDOA/FDOAaccuracyandcompensationestimationmethod[J].SystemsEngineeringandElectronicsm, 2016, 38(3): 481-486.]

[3]BetzJW.Comparisonofthedeskewedshort-timecorrelatorandthemaximumlikelihoodcorrelator[J].IEEETransactionsonASSP, 1984, 32: 285-294.

[4]BetzJW.Effectsofuncompensatedrelativetimeonabroad-bandcrosscorrelator[J].IEEETransactionsonASSP, 1985, 33(3): 505-510.

[5]AdamsWB.Correlatorcompensationrequirementsforpassivetimedelayestimationwithmovingsourceorreceivers[J].IEEETransactionsonASSP, 1980, 28: 158-168.

[6]HoshinoT,SuwaK,NakamuraS,etal.Long-timeintegrationbyshort-timecross-correlationandtwo-stepDopplerprocessingforpassivebistaticradar[C].The43rdEuropeanMicrowaveConference,Nuremberg,Germany,Oct. 7-10, 2013.

[7]MalanowskiM,KulpaK,OlsenKE.ExtendingtheintegrationtimeinDVB-Tbasedpassiveradar[C].The8thEuropeanRadarConference,Manchester,UK, 2011.

[8]BergeCR,DemissieB,HeckenbachJ.Signalprocessingfor

passiveradarusingOFDMwaveform[J].IEEEJournalofSelectedTopicsinSignalProcessing, 2010, 4(1): 226-238.

[9] 王慧，洪丽娜，易建新，等. 数字电视外辐射源雷达目标徙动补偿新方法[J]. 电子与信息学报, 2015, 37(5): 1017-1022. [WangHui，HongLi-na，YiJian-xin，etal.AnovelmigrationcompensationalgorithmforpassiveradarusingdigitalTVsignals[J].JournalofElectronics&InformationTechnology, 2015, 37(5): 1017-1022.]

[10] 黎剑兵，张双喜，苏大亮，等. 一种多普勒域走动校正的斜视SAR成像算法[J]. 宇航学报, 2016, 37(1): 118-126. [LiJian-bing,ZhangShuang-xi,SuDa-liang,etal.AsquintSARimagingalgorithmforlinearrangecellmigrationcorrectionindopplerdomain[J].JournalofAstronautics, 2016, 37(1): 118-126.]

[11]UlmanRJ,GeraniotisE.WidebandTDOA/FDOAprocessingusingsummationofshort-timeCAF′s[J].IEEETransactionsonSignalProcessing, 1999, 47(12): 3193-3200.

[12]UlmanRJ,GerantiotisE.MotiondetectionusingTDOAandFDOAmeasurements[J].IEEETransactionsonAES, 2001, 37(2): 759-764.

[13]WeissLG.Waveletsandwidebandcorrelationprocessing[J].IEEESignalProcessingMagazine, 1994, 11(1): 13-22.

[14] 罗海坤，王永庆，申宇瑶，等. 一种基于运动补偿的高动态微弱直扩信号捕获算法[J]. 宇航学报, 2013, 31(4): 539-545. [LuoHai-kun，WangYong-qing，ShenYu-yao，etal.AweakDSSSsignalacquisitionalgorithmbasedonmotioncompensationunderhighdynamicscenarios[J].JournalofAstronautics, 2013, 31(4): 539-545.]

[15] 董华安，王建国. 分布式相参射频探测系统信号积累方法综述[J]. 中国电子科学研究院学报, 2015, 10(1): 17-24. [DongHua-an,WangJian-guo.ReviewofsignalintegrationmethodsindistributedcoherentRFdetectionsystem[J].JournalofCAEIT, 2015, 10(1): 17-24.]

[16] 林茂庸，柯有安. 雷达信号理论[M]. 北京：国防工业出版社, 1981: 22-24.

[17] 严航，朱珍珍. 基于积分抽取的时/频差参数估计方法[J]. 宇航学报, 2013, 34(1): 99-105. [YanHang,ZhuZhen-zhen.FastalgorithmforjointestimationofDTOandDFObasedonintegrate-and-dumpfilters[J].JournalofAstronautics, 2013, 34(1): 99-105.]

通信地址：四川省成都市393信箱Z10分箱(610041)

电话：(028)86595385, 15102810081

E-mail:pearlpiggy7@21cn.com

Effect of Time-Varying TDOA/FDOA on Long-Time Coherent Integration and Compensating Strategy

ZHU Zhen-zhen1, LIU Li2

(1. National Key Laboratory of Blind Signals Processing, Chengdu 610041, China; 2. College of Information System and Management, National University of Defense Technology, Changsha 410073, China)

In a dual-GEO-satellite passive location system, the time-varying time difference of arrival (TDOA)/ frequency difference of arrival (FDOA) may induce the gain loss of the long-time coherent integration. Aiming at this problem, the

signal model with time-varying TDOA/FDOA is derived including both uplink and downlink relative motion. Then, according to the relationship between the regular signal’s autocorrelation function and energy spectrum density, the correlation peak magnitude loss in TDOA dimension is analyzed quantitatively; according to the frequency spectrum characteristics of the linear frequency modulation signal, the loss in FDOA dimension is analyzed quantitatively. Also, the compensating strategy and implementation procedure are provided. The validity of the compensation strategy and quantitative analysis is verified by processing the actual signal.

Dual-GEO-satellite passive location system; Long-time coherent integration; Correlation peak magnitude loss; Compensation of time-varying TDOA/FDOA

2017-02-08;

2017-05-02

TN96

A

1000-1328(2017)07-0735-08

10.3873/j.issn.1000-1328.2017.07.008

朱珍珍(1982-)，女，博士，主要从事数字信号处理与目标无源定位技术研究。