基于自适应RBF神经网络的可重复使用运载器再入段姿态控制*

窦立谦 田晓笛

天津大学电气与自动化工程学院，天津 300072



基于自适应RBF神经网络的可重复使用运载器再入段姿态控制*

窦立谦 田晓笛

天津大学电气与自动化工程学院，天津 300072

针对再入段可重复使用运载器(Reusable Launch Vehicles, RLV)姿态控制问题，提出一种基于自适应径向基函数(Radial Basis Function，简称RBF)神经网络(ARBFNN)的姿态控制方法。首先，建立RLV的6-DOF非线性动态模型，并将旋转动力学模型变成严反馈形式。然后，设计了一种自适应RBF神经网络控制(ARBFNN)结构，可以减少神经网络逼近误差的影响。同时，通过李雅普诺夫和自适应控制的结合消除了控制器设计过程中的不确定影响，并验证了系统的稳定性。最后，通过仿真验证了所提算法在解决再入段RLV姿态控制问题上的有效性。

姿态控制；RBF神经网络控制；可重复使用运载器

可重复使用运载器(简称RLV)是指可以多次重复使用，并自主往返地球与太空之间的多用途飞行器[1-2]。RLV再入过程的飞行马赫数和飞行高度跨度范围大，飞行条件恶劣，导致其模型具有强耦合、强非线性以及气动参数不确定性等特点[3]。因而，如何采用有效的控制方法，确保RLV能够在复杂的飞行环境下，拥有稳定的飞行特性以及良好的姿态跟踪控制性能，成为一个极具挑战性的问题。

近年来，飞行器再入过程的非线性控制方法取得了一定进展，一些先进的非线性控制技术开始在飞行器控制中使用。如文献[4]中针对再入飞行器, 设计了一种基于高阶滑模观测器的自适应时变滑模控制器。文献[5]提出了用神经网络自适应动态逆的方法控制飞行器，根据收敛误差和跟踪误差等性能提出了一种新的姿态角控制器，并采用自适应神经网络补偿模型误差。文献[6]提出了基于扩张状态观测器(ESO)的模糊自适应姿态控制方法，采用模糊自适应机制逼近姿态角动态的耦合不确定性，并采用ESO在线观测角速率动态中的综合不确定项，减轻计算负担。

神经网络具有大规模并行性的优点，对于任何复杂的非线性系统，它都具有快速适应能力和精确的近似能力，被广泛应用于飞行器姿态控制中[7]。文献[8]采用自适应神经网络与PID控制器相结合的方法，补偿系统的不确定性,同时对飞行状态的改变和飞行故障进行自适应调节。文献[9]以单输入单输出非线性系统为被控对象的基于神经网络的直接自适应控制方法，采用模糊推理系统估计控制误差，没有任何额外的控制神经网络自适应控制器，所有涉及到的信号都是指数稳定的，从而保证系统的稳定。文献[10]采用了自适应和反步相结合的控制方法使可重构飞行器具有更好的鲁棒性和稳定性。

本文在再入段RLV模型简化为严反馈形式的基础上，基于自适应方法和 RBFNN 相结合的思想提出了一种 ARBFNN 的控制系统。该系统由神经网络估计器和神经网络补偿器组成。其中，神经网络估计器由 ARBFNN充当，通过 ARBFNN估计飞行器的非线性动态模型；神经网络补偿器用来补偿神经网络估计值的误差。神经网络估计器和补偿器都通过自适应律调整相应参数的变化，消除了控制器设计过程中的不确定影响，并利用 Lyapunov 函数验证了系统的稳定性。

1 RLV模型及问题描述

1.1 RLV的动态模型

本文考虑类X-37B结构飞行器6自由度模型。模型在再入阶段为无动力飞行器，即推力为0，通过姿态调整逐渐减小飞行器马赫数。

飞行器的运动方程组为：

(1)

飞行器力矩方程组为：

(2)

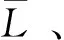
(3)

(4)

(5)

(6)

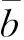
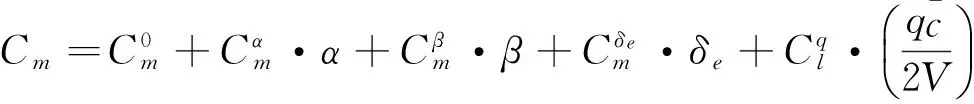
(7)

其中，α为攻角，β为侧滑角，δa,δe,δr分别表示副翼偏转角、升降舵偏转角和方向舵偏转角，C*表示后边项对应的气动系数。

1.2RLV模型化简

为了便于后面控制器的设计, 需要化简RLV模型为严反馈形式。将式(3)～(5)代入式(2)，可将式(2)化为如下标准形式：

(8)

其中,fp,fq,fr分别表示为：

fp=(c1r+c2p)q+c3Mx+c4Mz
fq=c5pr-c6(p2-r2)+c7My
fr=(c8p-c2r)q+c4Mx+c9Mz

(9)

而Mx,My,Mz分别表示为：

(10)

Gu可以表示为：

(11)

对式(1)进行二次微分，得到：

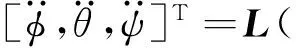
(12)

其中

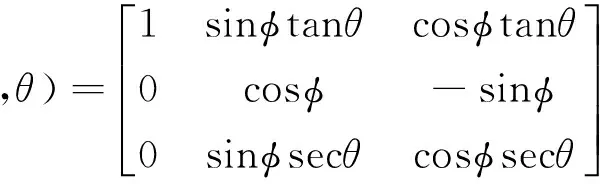
(13)

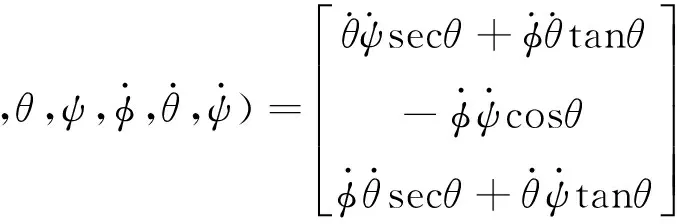
(14)

将式(8)代入式(12)中，得到：

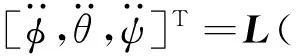
(15)

上式可以写成如下的二阶非线性系统：

(16)

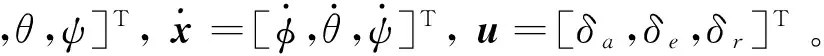
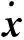
(17)

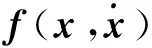
(18)

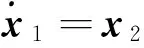
(19)

1.3 问题描述

再入段RLV的姿态控制目标：通过控制舵偏u实现对期望姿态角指令yd的渐进稳定跟踪，即

(20)

(21)

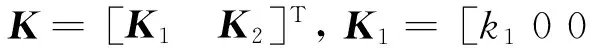
将式(21)代入式(19)中，得到：

(22)

为了保证系统稳定性，选取如下李雅普诺夫函数

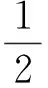
(23)

将式(23)对时间求导，并将式(22)代入，可得：

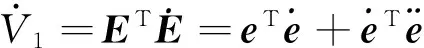
(24)

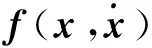
2 控制系统的设计及稳定性分析

2.1 基于RBF神经网络自适应系统的设计

基于ARBFNN的系统由神经网络估计器和神经网络补偿器构成，见图1，即

(25)

其中，fnn代表神经网络估计器的输出，fsc代表补偿器的输出。将式(25)代入式(21)可得控制律如下:

(26)

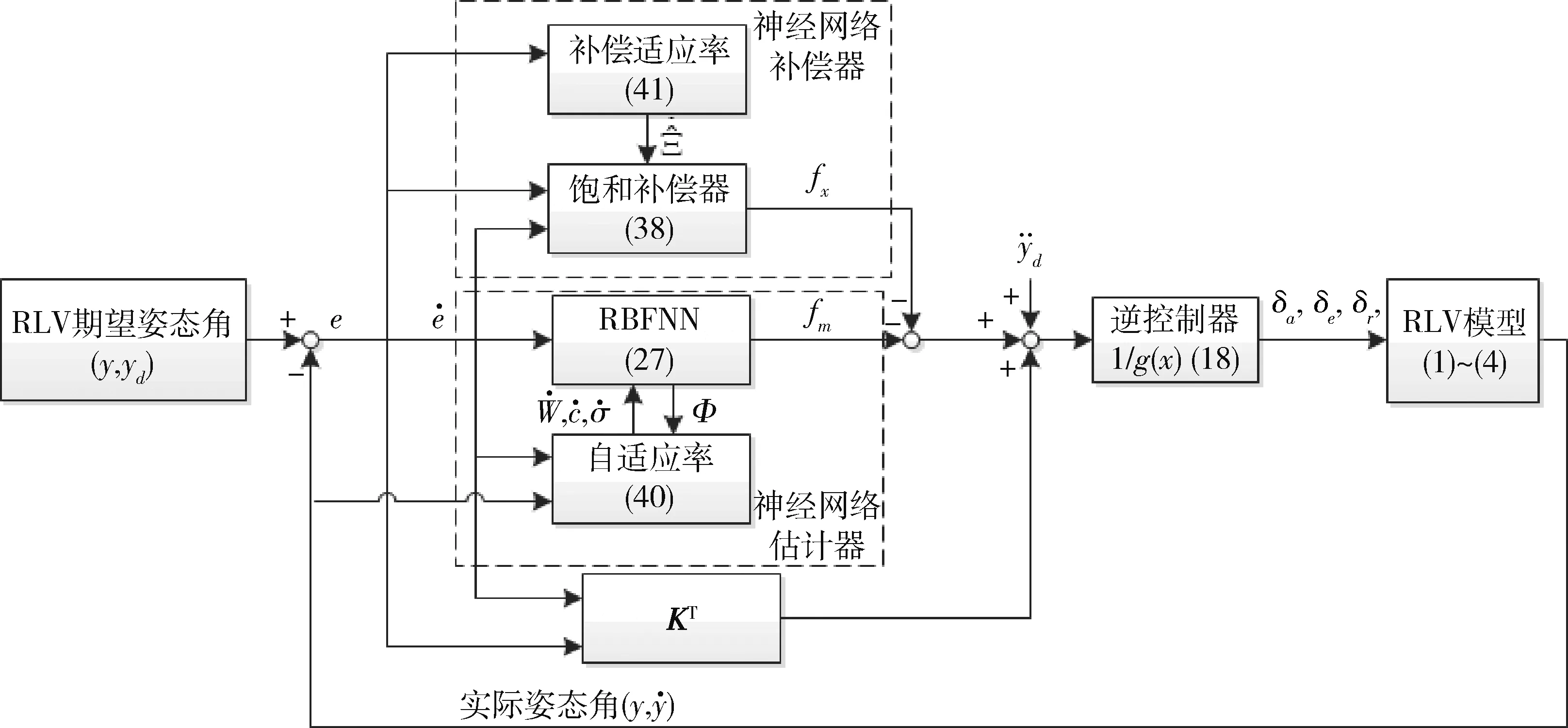
图1 控制系统的结构图

本文采用RBFNN与自适应相结合的控制方法，由神经网络估计器和神经网络补偿器组成，神经网络估计器用来估计飞行器的非线性动态模型，神经网络补偿器用来补偿神经网络估计值的误差，从而保证误差值最小，进而更为准确、快速地求解出飞行器的舵偏角控制量。利用ARBFNN充当估计器，只有确定系统的参数值和隐含层结点个数，才能确定ARBFNN的结构。隐含层节点数过多，则计算复杂；节点数过少，则精确度降低[12]。经过多次实验验证，选取3-12-3的结构。通过ARBFNN来估计fnn，ARBFNN的输出可以表示：

fnn=WTΦ(c,σ)

(27)

其中，W为隐含层输出的权值，W=[w1,w2，…，wn]=[w11,w12，…，w1n;w21，…，w2n，…，wmn]；c为隐含层神经元的高斯函数中心，c=[c11…,cn1,…,c1m,…,cnm]T；σ为径向基的宽度，σ=[σ11…,σn1,…,σ1m,…,σnm]T；Φ为径向基隐含层输出，Φ=[Φ1,Φ2,…,Φm]T(其中，m=12，n=3)。

设神经网络的期望输出为f*，神经网络的实际输出为f，由于神经网络估计器的输出是有误差的，所以它们的关系可以写成如下形式[13]：

f=f*+Δ=W*TΦ(c*,σ*)+Δ

(28)

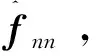
(29)

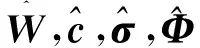
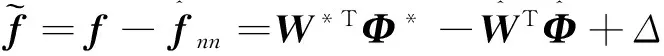
(30)

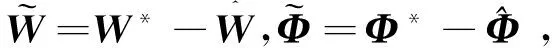
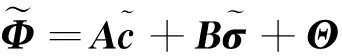
(31)

(32)

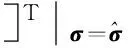
(33)

其中，

(34)

(35)

将式(31)代入式(30)得：

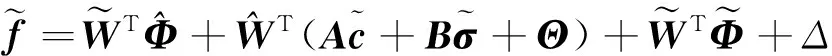
(36)

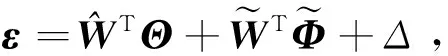
由式(21)～ (22)，(25)可得：

(37)

神经网络补偿器主要用来补偿神经网络的估计误差，设神经网络补偿器输出为fsc

(38)

ΛTP+PΛ=-Q

(39)

其中，Q为已知的正定矩阵。

2.2 稳定性分析

如果神经网络估计器选取自适应律为:

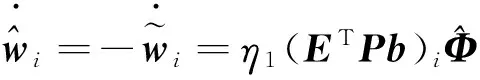
(40)

神经网络补偿器的误差估计律为:

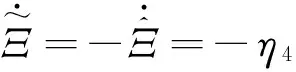
(41)

自适应RBF神经网络控制系统是稳定的，即当t→∞时，e(t)→0。选取正定的Lyapunov函数为：

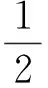
(42)

其中，η1,η2,η3,η4是已知的正数，表示学习效率。对式(42)求一阶微分，并将式(33)代入，可得：

(43)

其中，

(44)

(45)

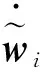
将式(40)代入(43)，则式(43)可写成

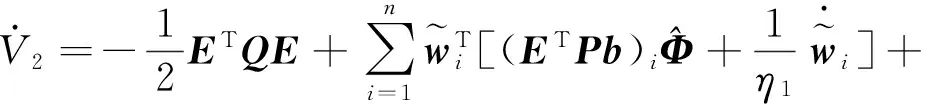
(46)

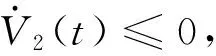
(47)

对式(47)积分可得：

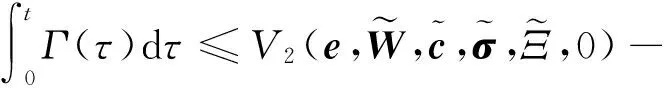
(48)

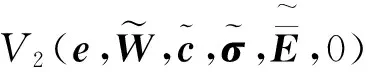
(49)

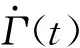
3 仿真验证

采用基于自适应RBF神经网络控制系统控制RLV的姿态，该控制系统的参数可以通过自适应律得到。为了验证系统良好的跟踪特性进行仿真，RLV的参数如表1所示。

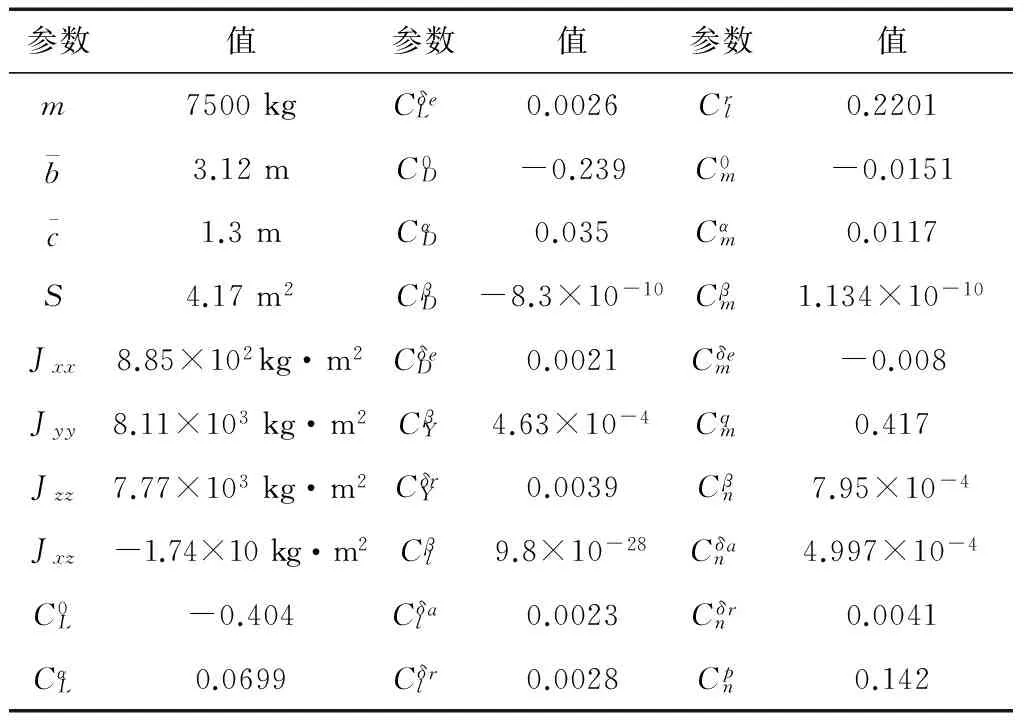
表1 RLV参数值

在仿真中，再入段RLV高度和速度的初始值分别为50km , 15Ma,初始空气动力学角度、姿态角和角速率包括β,φ,ψ,p,q和r为0，α=θ=25°，初始舵偏量等其他参数均为0。

如图2，系统的期望姿态角为

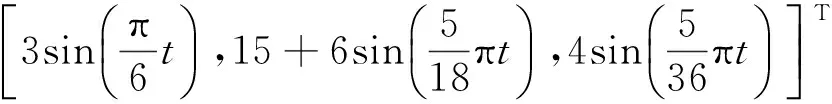
ARBFNN的输入为俯仰角，滚转角和偏航角的偏差。在Matlab下进行仿真，参数分别为k1=30,k2=5,η1=1,η2=η3=η4=0.2，采样时间为Ts=0.01s，舵面偏转角限制为±20°。实际RLV再入过程会根据需要调整姿态角，这里为了验证姿态角跟踪性能，仿真选择了正弦跟踪信号，仿真结果如图2～3。

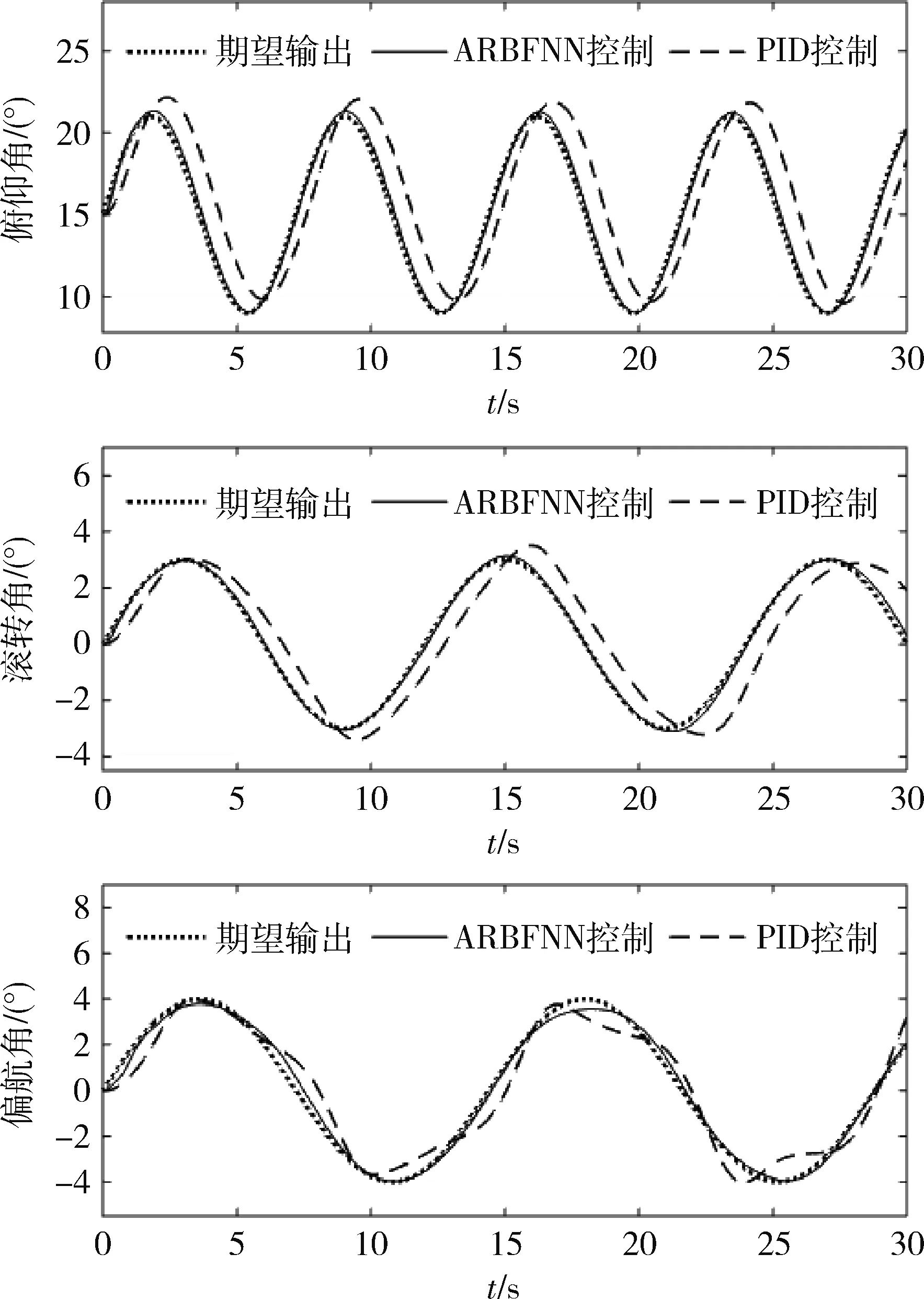
图2 姿态角跟踪曲线

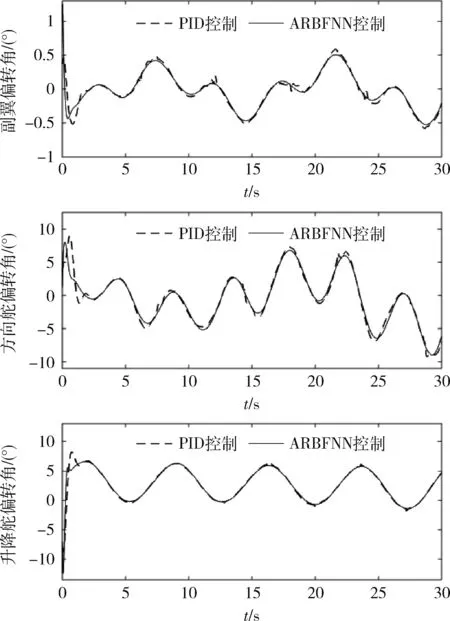
图3 舵偏角控制量输出曲线

仿真采用了ARBFNN 和传统的PID 控制方法，图2表明ARBFNN和传统的PID控制方法都能跟踪姿态角指令，但是，ARBFNN 的姿态角跟踪误差均小于PID的跟踪误差，跟踪性能更为优越。图3表明舵偏角的控制量均在可允许的范围内。

综上所述，本文所设计的控制器可确保RLV再入过程中控制系统具有良好的跟踪性和稳定性。

4 结论

针对再入RLV姿态控制问题，提出了一种基于自适应RBF神经网络的控制方法。以RBFNN为控制器，同时利用神经网络补偿器补偿系统的估计误差，其中控制器参数由自适应律得到，消除了控制器设计过程中的不确定影响，并利用李雅普诺夫验证了系统的稳定性。仿真结果表明本文所提出的控制方法能够实现对指令的实时跟踪。

[1] Shtessel Y B, Hall C E, Jackson M. Reusable Launch Vehicle Control in Multiple-time-scale Sliding Modes[J]. AIAA Journal of Guidance Control and Dynamics. 2000, 23 (6): 1013-1020.

[2] Jiang B, Gao Z F, Shi P, et al. Adaptive Fault Tolerant Tracking Control of Near Space Vehicle Using Takagi-Sugeno Fuzzy Models[J]. IEEE Transaction on Fuzzy Systems, 2010, 18(5): 1000-1007.

[3] 程志浩, 孙秀霞, 刘树光, 等.高超声速飞行器自适应神经网络动态面控制[J].飞行力学, 2013, 31(5): 425-428.(Cheng Zhihao, Sun Xiuxia, Liu Shu-guang, et al. Self-adaptive NNDynamic Surface Control of Hypersonic Vehicle [J]. Flight Dynamics, 2013,31 (5): 425-428.)

[4] 王亮, 刘向东, 盛永智. 基于高阶滑模观测器的自适应时变滑模再入姿态控制[J]. 控制与决策, 2014, 29(2):281-286.(Wang Liang, Liu Xiangdong, Sheng Yongzhi. High-order Sliding Mode Observer Based Adaptive Time-varying Sliding Mode for Re-entry Attitude Control [J]. Control and Decision, 2014, 29(2):281-286.)

[5] Gai W D, Wang H L, Zhang J, et al. Adaptive Neural Network Dynamic Inversion with Prescribed Performance for Aircraft Flight Control[J].Journal of Applied Mathe matics ,2013: 1-12.

[6] 胡超芳,刘运兵. 基于ESO的高超声速飞行器模糊自适应姿态控制术[J]. 航天控制, 2015, 33(3): 45-51.(Hu Chaofang, Liu Yunbing. Fuzzy Adaptive Attitude Control Based on ESO for Hypersonic Vehicles [J]. Aerospace Control, 2015, 33(3): 45-51.)

[7] 曾志峰, 汤一华, 徐敏, 等. 基于神经网络的飞行器再入制导研究[J]. 飞行力学, 2011, 29(3)：64- 67.(Zeng Zhifeng, Tang Yihua, Xu Min, et al. Study of Reentry Guidance Based on Neural Network [J]. Flight Dynamics, 2011，29(3)：64-67.)

[8] Savran A, Tasaltin R, Becerikli Y. Intelligent Adap- tive Nonlinear Flight Control for a High Performance Aircraft with Neural Network[J]. ISA Transactions, 2006, 45(2): 225-247.

[9] Chemachema M. Output Feedback Direct Adaptive Neural Network Control for Uncertain SISO Nonlinear Systems Using a Fuzzy Estimator of the Control Error[J]. Neural Networks,2012, 36: 25-34.

[10] Shin D H, Kim Y. Reconfigurable Flight Control System Design Using Adaptive Neural Networks[J]. IEEE Transactions on Control Systems Technology, 2004, 1(12):87-100.

[11] 吴森堂，费玉华. 飞行控制系统 [M]. 北京：北京航空航天大学出版社, 2005.(Wu Sentang, Fei Yuhua. Flying Control System [M]. Beijing: Press of Beijing University of Aeronautics & Astronautics, September, 2005.)

[12] Fan T, Wen R P. MEA For Designing Neural Network Weight and Structure Optimization[J].Computer Science and Information Engineering. 2009, 6: 111-115.

[13] Hsu C F. Adaptive Backstepping Elman-based Neural Control for Unknownn Onlinear Systems[J]. Neurocomputing, 2014,136: 170-179.

[14] Hus C F, Lin C M, Li M C. Adaptive Dynamic RBF Fuzzy Neural Controller Design with a Constructive Learning[J]. International Journal of Fuzzy Systems,2011, 13(3): 175-184.

Research on Attitude Control of Reentry for Reusable Launch Vehicles Based on Adaptive RBF Neural Network

Dou Liqian, Tian Xiaodi

School of Electrical and Automation, Tianjing University, Tianjin 300072, China

Anadaptiveradialbasisfunctionneuralnetworkcontrol(ARBFNNC)methodispresentedtoaddresstheattitudecontrolproblemofreentryforreusablelaunchvehicles(RLV).Firstly,the6-DOFnonlineardynamicmodelofRLVisestablishedandtherotationaldynamicsandrotationalkinematicaretransformedintostrict-feedbacksystem.Hence,anARBFNNCsystemstructureisestablishedwhichcanbenefittoreducetheeffectsoftheapproximationerrorofneuralnetwork.Then,bycombiningtheadaptivemethodwithLyapunovfunction,thestabilityofsystemisguaranteedandtheuncertaineffectintheprocessofcontrollerdesigniseliminated.Finally,anumericalsimulationisemployedtoillustratetheeffectivenessoftheproposedstrategybysolvingproblemofattitudecontrolaccuracyandthesystemrobustness.ThesimulationresultsdemonstratethattheARBFNNCsystemcanachievefavorablecontrolperformanceaftertheparameterlearningoftheARBFNN.

Attitudecontrol; RBFneuralnetwork;Reusablelaunchvehicles

* 国家自然基金项目(91016018,61074064)

2016-04-21

窦立谦(1976-)，男，河北人，博士，副教授，主要研究方向为复杂系统建模与控制、飞行器建模与控制；田晓笛(1991-)，女，河北人，硕士研究生，主要研究方向为飞行器控制。

TP273

A

1006-3242(2017)01-0025-06