北斗系统整周模糊度及周跳的确定算法*

李冬霞 宋馥含 刘瑞华

中国民航大学电子信息与自动化学院，天津300300



北斗系统整周模糊度及周跳的确定算法*

李冬霞 宋馥含 刘瑞华

中国民航大学电子信息与自动化学院，天津300300

在进行卫星导航定位时，利用载波相位比利用码相位进行定位拥有更好的定位精度和安全性，并可以提升用户的满意度，然而得到测相伪距的前提是明确载波相位的整周模糊度和周跳数。首先根据三频模糊度分解模型将整周模糊度解算出来；然后利用三频码伪距/载波相位组合法进行周跳数的求解；最后仿真验证了整周模糊度解算方法的正确性，并分析比较多频接收机型号的不同对卫星信号周跳值的影响。

载波相位；整周模糊度；周跳

全球导航卫星系统(Global Navigation Satellite System, GNSS)接收机对每颗卫星产生伪距和载波相位2个基本距离观测值。通常伪距测量值比较粗糙，接收机码跟踪环路只能将码相位确定到几米的精度；而接收机载波跟踪环路对载波相位的测量精度可达几毫米左右[1]。因此，载波相位观测值在卫星导航定位中有更高的利用价值。

为了有效利用载波相位距离观测量，需要确定整周模糊度。同时，导航定位接收机在观测中由于障碍物遮挡或无线电干扰等原因，卫星信号会出现短时间失锁，引发周跳[2]。周跳现象的产生将破坏观测数据的连贯性，导致导航系统定位精度下降。因此，采用有效算法解算整周模糊度，并准确探测周跳是提高GNSS系统载波相位观测精度的关键因素。

针对整周模糊度解算问题，国内外学者提出了多种解算整周模糊度的方法：如模糊度函数法[3-4]、最小二乘模糊度搜索法[5]和最小二乘模糊度去相关法[6]等。研究表明，以上方法均是基于双差或三差观测方程解算整周模糊度，其缺点在于至少要知道一个参考站的观测信息，且其精度受长短基线的影响[7-8]，解算效率降低。传统的周跳探测方法有高次差法、多项式拟合法、电离层残差法以及Kalman滤波等方法[9]。这些方法都是基于单频和双频数据探测周跳，很难将卫星原始观测信号的周跳彻底消除。基于多频组合进行周跳探测和模糊度解算的方法中，使用最广泛的是Melbourne和Wubbena于1985年提出的Melbourne-Wubbena 组合(简称MW组合)[10-11]和码伪距/载波相位组合，MW组合方法可用于GPS系统周跳的探测与修复[12-13]，码伪距/载波相位组合方法可用于GPS系统整周模糊度的确定[14]。三频组合数据的处理不仅可以提高定位精度，而且可以提高原始数据预处理的质量[15]。

本文基于北斗系统B1，B2，B3三个频段的实际导航信号观测值，研究北斗系统卫星信号整周模糊度以及周跳数确定算法。给出利用MW组合以及三频模糊度分解模型解算整周模糊度的具体方法，以及利用三频码伪距/载波相位组合求解周跳数的具体方法。构建北斗系统信号分析实验环境，验证了上述方法的有效性。

1 整周模糊度及周跳的求解方法

1.1 整周模糊度的解算方法

本文整周模糊度值的解算分为2个步骤：首先通过MW 组合求出组合观测值的整周模糊度值，然后利用三频模糊度分解模型解算出单频载波的整周模糊度值。

MW 组合实质为宽巷相位伪距与窄巷码伪距的组合，组合观测值LM-W表示为[15-18]：

(1)

式中，(1/(f1-f2))(f1L1-f2L2)为宽巷载波相位伪距组合；(1/(f1+f2))(f1P1+f2P2)为窄巷码伪距组合；L1，L2分别代表北斗B1载波、B2载波上的测相伪距；P1，P2分别代表北斗B1载波、B2载波上的测码伪距；f1，f2分别代表北斗B1载波、B2载波的频率。

MW组合观测值的整周模糊度可以表示为：

NM-W=LM-W/λM-W=LM-W(f1-f2)/c

(2)

式中，NM-W代表MW组合整周模糊度；λM-W代表MW组合波长，c代表真空中的光速。

假设载波和伪距的观测方程分别为：

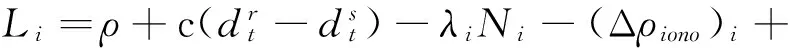
(3)

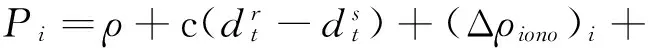
(4)

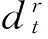
令与频率无关的误差总和为Δρ，假设电离层延迟至一阶项，则上述方程可写为：

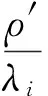
(5)

(6)

式(5)和(6)中，ρ′=ρ+Δρ；φi(i=1,2,3)分别代表北斗各载波的相位；A=80.62m3·s-2代表电离层折射率。通过式(5)和(6)可以得到北斗各载波的整周模糊度的差值以及ρ′，为：

(7)

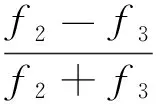
(8)

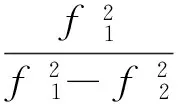
(9)

根据式(2)所示，令N2-N1=NL1-L2，N3-N2=NL2-L3，通过式(5)减式(8)得：

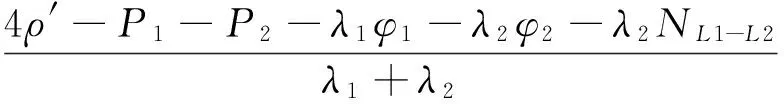
(10)

N2=N1+NL1-L2

(11)

N3=N2+NL2-L3

(12)

求解以上各式得到单频载波的整周模糊度值。

1.2 周跳的探测与修复方法

本文使用三频码伪距/载波相位组合方法修复周跳[12-13,15-18]。伪距观测方程引用式(4)中任一载波的测码伪距，载波相位组合观测方程为：

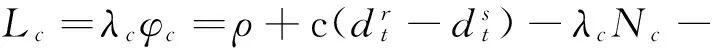
(13)

式中，Lc，λc，φc和Nc分别代表利用载波相位组合观测值得到的伪距、波长、相位和整周模糊度。选取一组线性无关值i，j，k，则λc，φc和Nc分别表示如下：

λc=λ1λ2λ3/(iλ2λ3+jλ1λ3+kλ1λ2)

(14)

φc=iφ1+jφ2+kφ3

(15)

Nc=iN1+jN2+kN3

(16)

将式(4)中任一载波的测码伪距和式(13)相减，可得：

(17)

将式(17)在历元间相减，可得：

(18)

式中，ΔNc代表载波相位组合观测值的周跳；Nc(t1)和Nc(t2)分别代表组合观测值在t1，t2历元的整周模糊度值；φc(t1)，φc(t2)分别代表t1，t2历元的载波相位组合观测值；Pi(t1)，Pi(t2)分别代表t1，t2历元在北斗任一载波的伪距观测值。组合后的载波相位观测值的周跳为：

ΔNc=iΔN1+jΔN2+kΔN3

(19)

由于长波长的组合观测值对于确定整周模糊度有利，因此选取3个长的组合波长且线性无关的观测值组合(i1,j1,k1)，(i2,j2,k2)和(i3,j3,k3)，本文选取的线性无关组合为(0，1，-1)，(3，0，-4)和(-7，9，0)，根据式(19)可得：

(20)

式中，ΔN1，ΔN2，ΔN3为3种组合观测值探测的周跳值；n1，n2，n3分别为3个载波上的周跳值，通过求解线性方程组 (20) 即可求得。

2 实测数据分析

根据多系统多频点接收机在中国民航大学实验室(北纬39.112 588 661°，东经117.344 275 744°)于2015年9月8日至14日观测的实际运行卫星的原始观测数据，以2015年9月8日和9日数据为例进行实测数据分析，验证本文推导出的整周模糊度解算的正确性，根据北斗系统和GPS系统实际卫星运行数目，利用不同接收机接收到的卫星信号实测瞬时多普勒数据，得到积分多普勒值，即多普勒频移引起的载波相位变化值，然后通过卫星信号原始载波相位变化值和伪距观测值，给出北斗系统和GPS系统整周模糊度和周跳数的实验结果。

2.1 实验参数

表1给出了GNSS系统信号实验环境的主要技术参数。

2.2 实验结果

图1为北斗系统161号卫星分别在B1，B2和B3载波上的整周模糊度随历元变化规律曲线，图中选取200个点的整周模糊度值。接收机处理之后的北斗161号卫星观测数据(包括整周数部分和不足一周的小数部分)为：在B1载波的载波相位为196796884.883907周，B2载波的载波相位为152175747.034031周，B3载波的载波相位为159913485.194586周，与图1所示的北斗161号卫星对应载波的整周模糊度值基本相近，可验证本文模糊度求解算法合理。

图1 北斗161号卫星各个载波的整周模糊度曲线

图2为北斗系统174号卫星分别在B1，B2和B3载波上的整周模糊度随历元的变化规律曲线。图中选取500个点的整周模糊度值。接收机处理之后的北斗174号卫星观测数据显示，在B1，B2和B3载波的载波相位分别为124889563.191117周、96572528.335204周和101482965.962124周。与图2所示的北斗174号卫星对应载波的整周模糊度值基本一致，可验证模糊度求解算法合理。

图2 北斗174号卫星各个载波的整周模糊度曲线

图3为北斗系统161号卫星分别在B1，B2和B3频率上的周跳数随历元变化规律曲线，图中选取200个历元进行说明。由图可看出： 1)北斗系统161号卫星B1频率上的周跳数比其他2个载波上的周跳数更多； 2)北斗系统161号卫星3个频率上的周跳数均在30～130周之间波动。

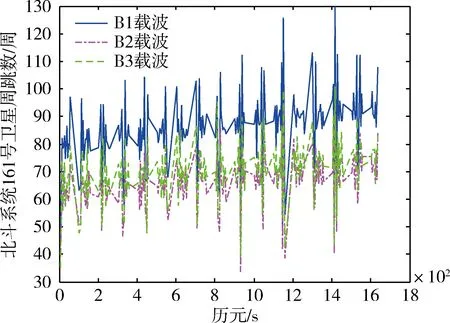
图3 北斗161号卫星各个频率的周跳数曲线(200个点)

图4为北斗系统174号卫星分别在B1，B2和B3频率上的周跳数随历元的变化规律曲线，图中选取500个历元进行说明。由图可看出： 1)北斗系统174号卫星B1频率上的周跳数比其他2个载波上的周跳数更多；2)北斗系统174号卫星3个频率上大部分历元的周跳数均在2000～15000周之间波动，说明由于卫星信号在传播过程中，受到干扰较大，导致出现较大的周跳。

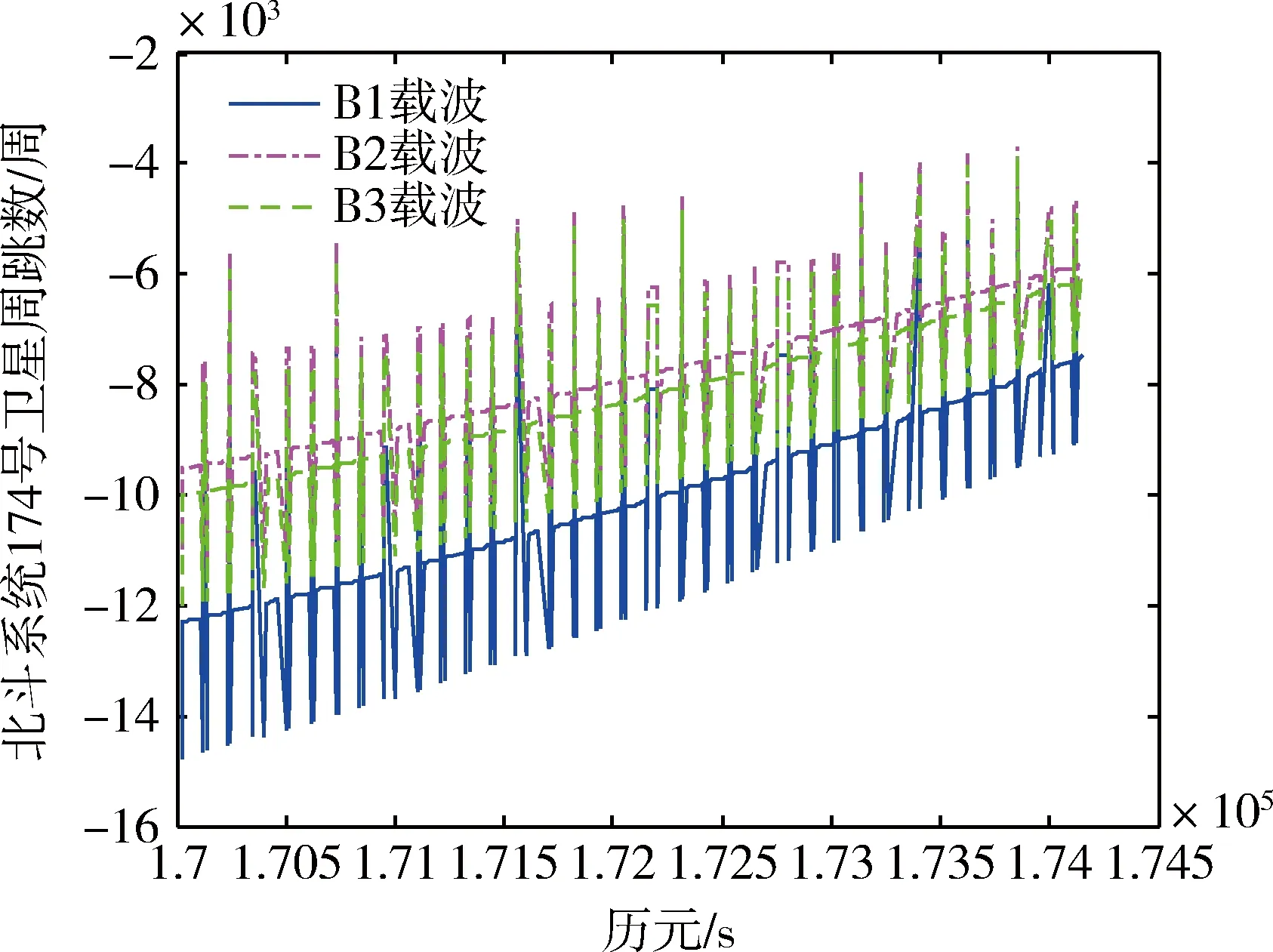
图4 北斗174号卫星各个频率的周跳数曲线(500个点)

本文只给出了北斗系统161号和174号卫星的周跳数曲线，其他11颗卫星的周跳数曲线性质均与161号、174号卫星一致，不再赘述。

图5和6为BDM670接收机接收的48h GPS系统观测数据计算得到的1号、30号卫星分别在L1和L2频率上的周跳数随历元变化规律曲线。由图可看出： 1) GPS系统1号和30号卫星L1频率上的周跳数比L2频率上的周跳数更多； 2)通过将该接收机接收的GPS系统观测数据进行处理，得到的周跳数比较大，说明卫星信号在传播过程中，受到干扰较大，导致出现较大的周跳。

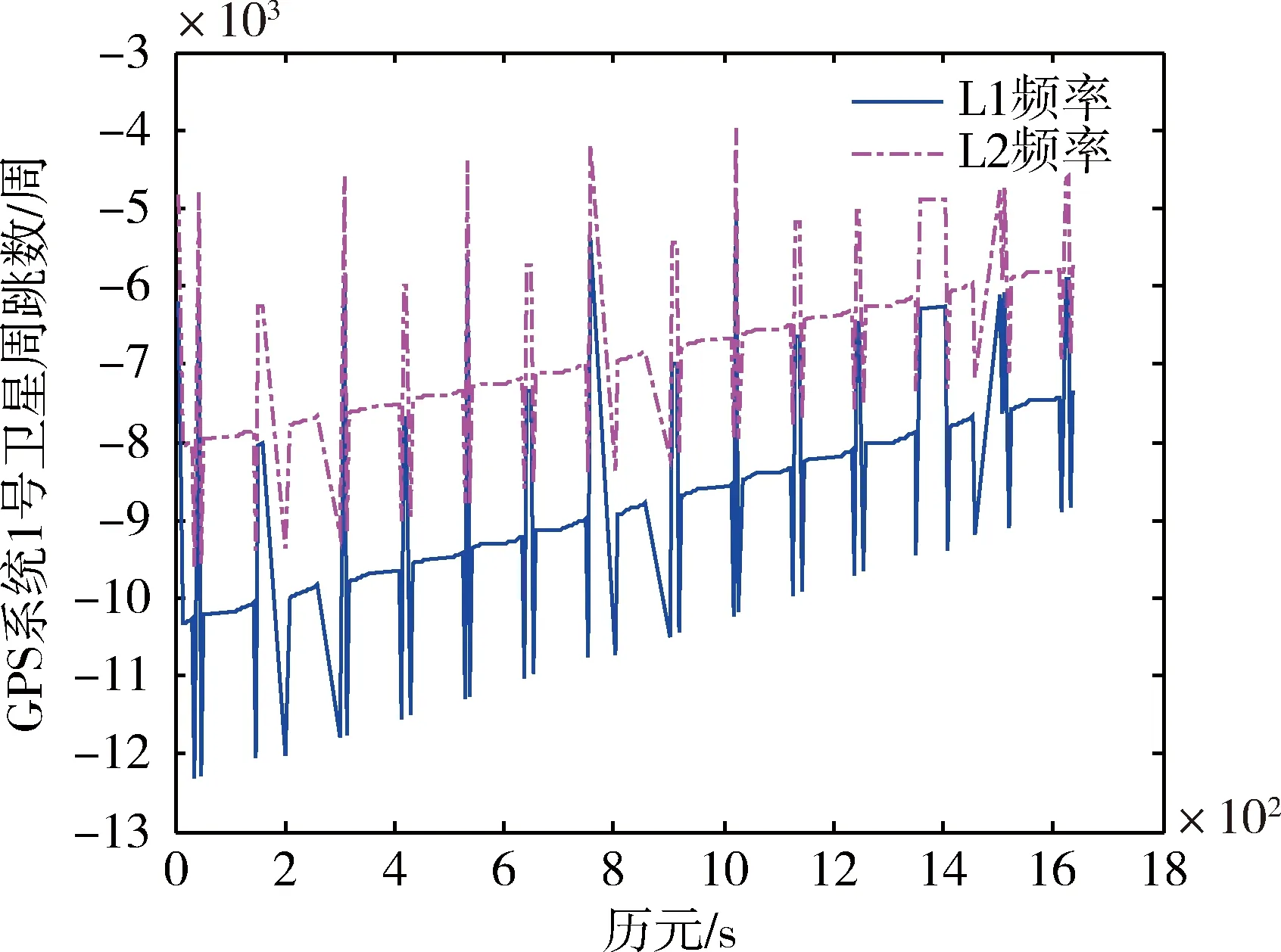
图5 GPS系统 1号卫星各个载波的周跳数曲线

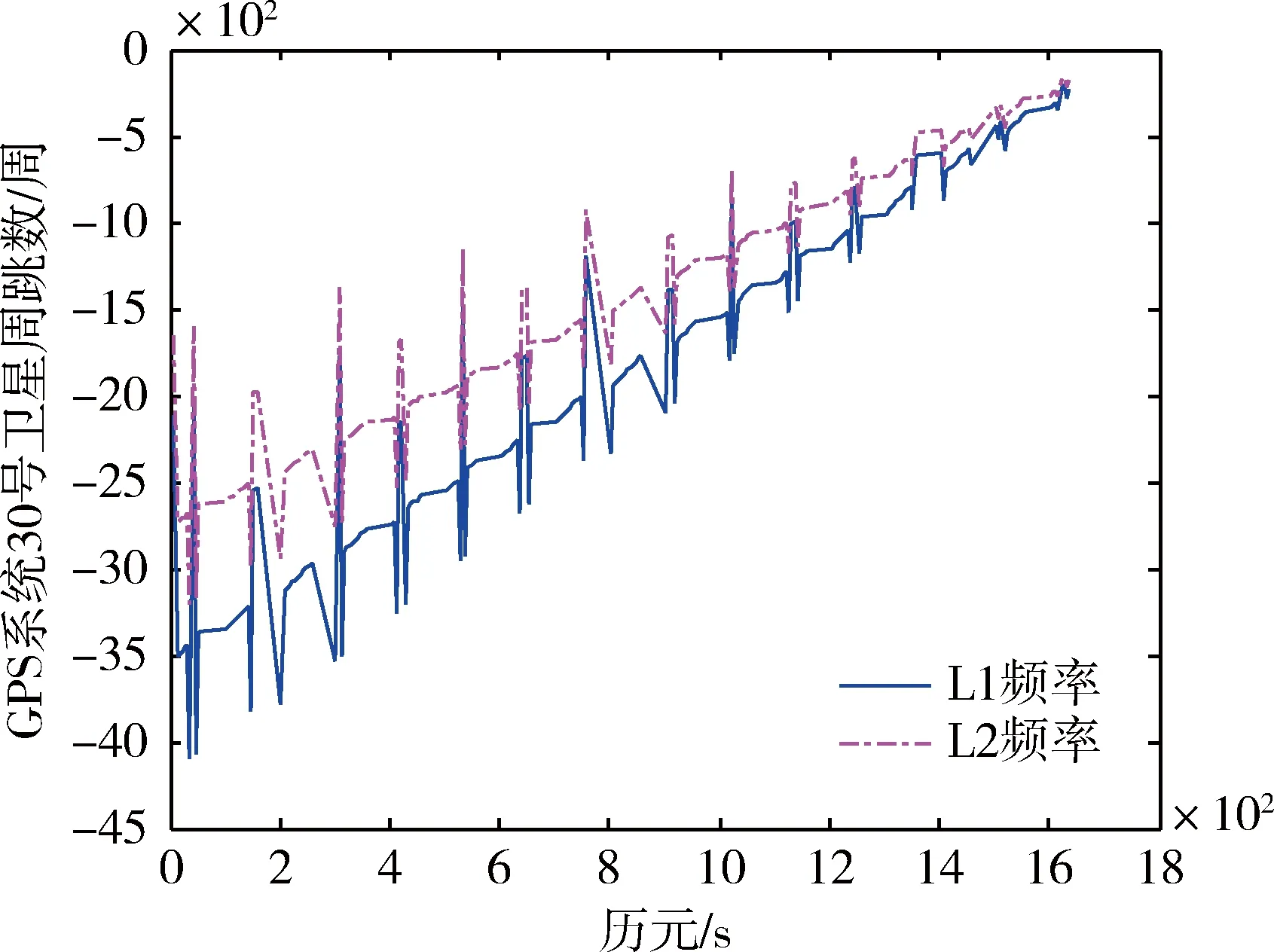
图6 GPS 30号卫星各个载波的周跳数曲线

本文只给出了GPS系统1号和30号卫星的周跳数曲线，其他28颗卫星的周跳数曲线性质均与这几颗卫星一致，不再赘述。

3 结论

证明了仅利用非差单点多频接收机接收卫星观测数据，并通过Melbourne-Wubbena 组合和三频模糊度分解模型即可将载波相位的整周模糊度快速解算出来，计算机仿真验证了理论分析的正确性；接收机型号的不同导致卫星载波周跳值不同，从而对卫星导航定位的精度产生很大影响。

基于本文研究结论，可将多频组合观测值运用于整周模糊度以及周跳的快速求解，以进行卫星导航定位，也可将其运用于卫星测距码与载波一致性的评估与验证。

[1] 谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2009:77.(Xie G.Principles of GPS and Receiver Design[M].Beijing: Electronics Industry Press,2009:77.)

[2] 谭兆伟.GPS精密单点定位周跳探测与修复方法研究[D].青岛:山东科技大学,2009:6-9.(Tan Z W.Investigations on Cycle Slip Detection and Correction in GPS Precise Point Positioning[D].Qingdao:Shandong University of Science and Technology,2009:6-9.)

[3] Benjamin W.Remondi.Pseudo-kinematic GPS Results Using the Ambiguity Function Method[J].Journal of The Institute of Navigation,1991,42(1):109-165.

[4] Han S，Rios C. Improving the Computational Efficiency of the Ambiguity Function Algorithm[J].Journal of Geodesy,1996,70(6):330-341.

[5] Hatch R.Instantaneous Ambiguity Resolution[C]//Proceedings of KIS’90.Banff,Canada,10-13 September 1990:299-308.

[6] Teunissen P J G.A New Method for Fast Carrier Phase Ambiguity Estimation[C]//Proceedings of IEEE PLANS’94. Las Vegas, NV, April 11-15 1994:562-573.

[7] 陈树新.GPS整周模糊度动态确定的算法及性能研究[D].西安:西北工业大学,2002:9-11. (Chen S X.A Study of the Algorithm and Its Performance for GPS Ambiguity Resolution on the Fly[D].Xi’an:Northwestern Polytechnical University,2002:9-11.)

[8] 韦建超.GPS精密单点定位的数据处理研究[D].长沙:中南大学,2007: 1. (Wei J C.A Study on GPS Precise Point Positioning Data Processing[D].Changsha: Northwestern Polytechnical University,2007:1.)

[9] 生仁军.GPS载波相位定位中周跳探测方法的研究[D].南京:东南大学,2006:21-46. (Sheng R J.Investigations on Cycle Slip Detection in GPS Carrier Phase Positioning[D].Nanjing:Southeast University,2006:21-46.)

[10] Beutler G, Bauersima,Cimbalnik.Ambiguity Resolution Techniques in Geodetic and Geodynamic Applications of the Global Positioning System[R].University of Berne，2000.

[11] 冯来平.GPS多频观测数据处理方法及应用研究[D].郑州:解放军信息工程大学,2009: 30. (Feng L P.A Study on Processing and Application of GPS Muti-Frequency Observations Data[D].Zhengzhou:PLA Information Engineering University,2009: 30.)

[12] 熊伟,伍岳,孙振冰,等.多频数据组合在周跳探测和修复上的应用[J].武汉大学学报,2007,32(4):319-322. (Xiong Wei,Wu Yue,Sun Zhenbing,et al.Application of Cycle Slip Detecting and Repairing Using Multi-frequency Combination Observation[J].Engineering Journal of Wuhan University, 2007,32(4):319-322.)

[13] 汪平,郝金明,刘伟平,等.使用多频组合观测值探测与修复周跳[J].测绘通报,2009,6:12-15. (Wang Ping,Hao Jinming,Liu Weiping,et al.Cycle Slip Detecting and Repairing Using Multi-frequency Combination Observation[J]. Bulletin of Surveying and Mapping,2009,6:12-15.)

[14] 黄丁发,周乐涛,李成刚,等.GPS增强参考站网络理论[M].北京:科学出版社,2011:113-114. (Huang Dingfa, Zhou Letao,Li Chenggang,et al.Augmentation Reference Station Network Theory of GPS[M].Beijing:Science Press, 2011:113-114.)

[15] 原波.基于GPS三频非差相位精密单点定位算法研究及程序实现[D].北京:清华大学,2012: 1-75.

(Yuan Bo.The Algorithms and Program Implementation of Precise Point Positioning Based on GPS Tri-frequency Carrier Phase Observations[D].Beijing: Tsinghua University,2012: 1-75.)

[16] 黄丁发, 周乐涛, 李成刚, 等. GPS增强参考站网络理论[M]. 北京: 科学出版社, 2011: 113-114. (Huang Dingfa, Zhou Letao, Li Chenggang, et al. Augmentation Reference Station Network Theory of GPS[M]. Beijing: Science Press, 2011: 113-114(in Chinese).)

[17] 李卫军,姜卫平,王泽民.GPS载波相位三频组合观测值的模型研究[J].测绘信息与工程,2008,33(3):6-8.(Li Weijun, Jiang Weiping, Wang Zemin. Reserch on the Model of GPS Triple-frequency Phase Combination Observations[J].Journal of Geomatics, 2008,33(3):6-8.)

[18] Radovanovic R S, Fotopoulos G, El-Sheimy N. On Optimizing GNSS Multi-frequency Carrier Phase Combinations for Precise Positioning[C]. Presented at The International Association of Geodesy 2001 Scientific Assembly, Budapest, Hungary, Sept 2-7.

The Determination Algorithms of Integer Ambiguity and Cycle Slip in BDS

Li Dongxia，Song Fuhan，Liu Ruihua

College of Electronic Information and Automation, Civil Aviation University of China, Tianjin 300300, China

Theaccuracyofpositioningandsecuritycanbeobtainedbetterbyusingcarrierphasethancodephasewhensatelliteisundernavigationandpositioning,andcustomersatisfactioncanbeimproved.Butthepremiseofgettingphasepseudorangemeasurementisthedeterminationofintegerambiguityandcycleslip.Firstly,theintegerambiguityiscalculatedbasedontri-frequencyambiguitydecompositionmodel.Then,thecycleslipisdetectedbymeansofcombinationofmulti-frequencypseudorangecodeandcarrierphase.Finally,thevalidityofresolvingintegerambiguityisverifiedbysimulationsandtheinfluenceofdifferentreceiversoncycleslipofsatellitesignalsiscompared.

Carrierphase;Integerambiguity;Cycleslip

* 民航安全能力建设基金(ADDSA0007)

2016-07-22

李冬霞(1971-)，女，陕西人，博士，副教授，主要研究方向为航空移动通信、甚高频数据链；宋馥含(1991-)，女，哈尔滨人，硕士研究生，主要研究方向为卫星导航在民航中的应用；刘瑞华(1965-)，男，陕西人，博士，教授，主要研究方向为卫星导航在民航中的应用、卫星导航与组合导航。

TN967.1

A

1006-3242(2017)01-0066-05