基于实时相对测量的航天器指向跟踪控制问题研究

徐广德 闫 鑫 苟仲秋 张柏楠

中国空间技术研究院载人航天总体部，北京100094



基于实时相对测量的航天器指向跟踪控制问题研究

徐广德 闫 鑫 苟仲秋 张柏楠

中国空间技术研究院载人航天总体部，北京100094

针对大型挠性航天器指向跟踪控制问题，提出一种期望姿态估计方法和基于反步法的姿态跟踪控制方法。首先采用平方根容积卡尔曼滤波进行相对轨道估计，利用相对位置估计信息解算出追踪航天器观测轴指向目标航天器的期望姿态。然后基于修正Rodrigues参数描述的误差姿态动力学方程设计了姿态控制器，考虑系统惯量的不确定性设计了自适应控制律。最后将该方法应用到某空间观测任务中，仿真结果表明了方法的有效性。

相对测量；姿态跟踪；反步法；单框架控制力矩陀螺

姿态指向跟踪控制在卫星编队飞行、空间激光通信、在轨服务和空间攻防对抗等领域具有重要作用。在这些任务中，往往需要航天器对合作或非合作目标进行大角度快速指向跟踪，对动目标跟踪指向精度与目标的动态特性、期望姿态的测量精度、卫星姿态测量精度、控制算法和执行机构的能力等有关。要跟踪精准，首先要测量精准，因此要求期望姿态具有较高的测量精度。与常规的姿态稳定控制不同，高精度的快速姿态跟踪还要求控制器具有快速响应能力。

文献[1]研究了刚体卫星的高精度大角度指向跟踪控制问题，设计了PD型姿态指向跟踪控制器，可同时实现角度跟踪和角速度跟踪。为提高控制精度同时避免控制输出进入饱和域，在控制器的基础上设计了增益分配律。文献[2]研究了挠性航天器掠飞观测目标时的建模与控制问题，给出了一种期望姿态求解方法，但在大角度机动时容易出现奇异；设计了自适应滑模控制律，但没有考虑期望姿态存在的误差和执行机构的实际输出能力限制。文献[3]研究了与非合作目标编队飞行过程中，保持从星姿态指向目标星的控制方法，在解算期望姿态时只测量了相对位置，节省了测量设备，研究对象是刚体小卫星。文献[4]研究了空间绕飞任务中从航天器对主航天器进行观测时的姿态跟踪控制问题，根据相对运动的位置和速度，解算了从航天器的期望跟踪姿态。文献[5]研究了利用大椭圆轨道卫星与GEO目标期间进行观测的视线跟踪控制问题，给出了交会过程中视线轴期望指向姿态，设计了终端滑模跟踪控制律并分析了稳定性，研究对象是小卫星，未考虑挠性附件影响，且未对执行机构输出力矩限幅。文献[6-7]研究了航天器对空间移动目标的跟踪控制问题，但该方法对期望角速度和期望角加速度的求解复杂。文献[8]针对大椭圆轨道卫星交会高轨卫星期间的相对姿态指向控制需求，提出了一种采用混合执行机构的快速、高精度视线跟踪姿态控制方法，相对距离在100km以内的快速交会阶段的视线跟踪控制精度达0.005°，未考虑期望指向的误差和执行机构力矩噪声。文献[9]针对存在外部干扰和模型不确定性的航天器，提出了一类新颖的基于自抗扰技术的控制方案，实现无姿态角速度反馈的航天器对目标高精度姿态指向控制。以上文献研究对象多为刚体卫星，对于大型挠性卫星的快速随动指向问题研究较少，虽然都给出了期望姿态的求解方法，但未考虑期望姿态的测量误差对最终指向精度的影响。

针对上述问题，本文首先建立了非线性的相对轨道动力学模型和测量模型，给出基于平方根容积卡尔曼滤波的相对轨道确定方法，用滤波得到的相对位置和速度信息解算实时的期望姿态。然后基于带挠性附件和控制力矩陀螺群的姿态动力学模型，考虑系统惯量的不确定性，设计了反步自适应控制律来实现姿态跟踪。最后将该方法应用于某空间观测任务，进行了数学仿真，验证了基于实时相对测量得到期望姿态的精确性和控制方法的有效性。

1 相对测量问题

首先给出通过滤波求解相对位置的方法，然后给出期望姿态解算方法。假设追踪航天器的载荷安装在本体x轴上，控制追踪航天器本体x轴与视线方向重合，指向目标航天器。

1.1 相对轨道确定

1.1.1 相对轨道动力学模型

[10]，可得在追踪星轨道系下建立的非线性动力学模型：

式中，x，y，z为相对位置分量，rc为追踪星地心距，μ为引力常量。

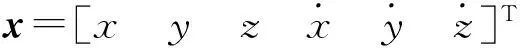
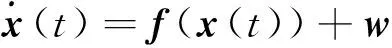
其中，w为系统误差，如果系统的过程噪声矩阵为Q，则w与Q之间的关系为E[wwT]=Qδ(t-τ)。

1.1.2 测量模型

假设追踪星上装有大视场捕获测角相机，可测得目标相对于追踪星的相对方位：

1)追踪星指向目标星的矢量与本体系xy平面的夹角，即仰角δ；

2)追踪星指向目标星的矢量在本体系xy平面的投影与x轴的夹角，即方位角ε。

则测量值与本体系下相对位置ρct=[xct,yct,zct]T的关系为

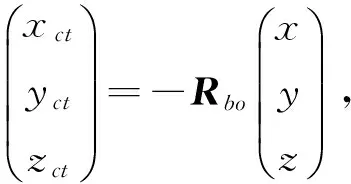
可以得到描述测量值Z=[δε]T与状态向量x关系的测量方程为

Z=h(x(t))+v

其中，v=[vδvε]为设备的测量误差。

1.1.3 滤波算法

滤波算法采用平方根容积卡尔曼滤波，不需要计算状态转移矩阵和雅克比矩阵，只需将状态方程和测量方程代入滤波框架中，限于篇幅不做介绍，具体算法见参考文献[11]。

1.2 期望姿态解算

设期望坐标系相对追踪航天器轨道系的坐标转换矩阵为Rdo，定义如下：

Rdo=[ijk]

(1)

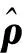
期望姿态角速度为ωd:

(2)

(3)

2 指向控制问题

2.1 带SGCMGs挠性卫星动力学建模

使用N个单框架控制力矩陀螺，卫星姿态动力学方程和挠性附件的振动方程如下[12]：

(4)

式中有关参数含义请见文献[12]。

对于单框架控制力矩陀螺，转子转速恒定，得到如下动力学方程：

(5)

τc为SGCMGs作用于航天器的力矩

(6)

式中，B=AgIcg,C=AtIws[Ω]d+(ω+Rboωo)×·AgIcg。

用修正罗德里格斯参数(MRP)来描述航天器本体相对于轨道坐标系的姿态，定义如下

σ=ηtan(φ/4)

式中，η为欧拉转轴方向矢量，φ为欧拉转角。

运用MRP表示的姿态运动微分方程如下

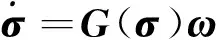
(7)

其中，

2.2 反步自适应控制律

σd为期望坐标系Sd相对于追踪航天器轨道系So的姿态，可通过式(1)得到。σe为追踪航天器本体系Sb相对于Sd的姿态：

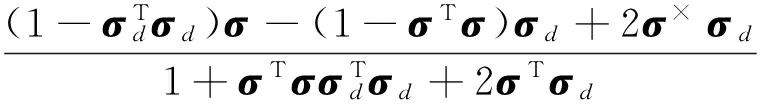
ωe为Sb相对于Sd的角速度在Sb的分量列阵

ωe=ω-Rbdωd

(8)

式中，Rbd为Sd到Sb的坐标转换矩阵。

由式(7)可知，σe和ωe满足关系式

将式(8)求导，代入式(5)，得误差动力学方程为：

(9)

则姿态控制的目标是σe→0，ωe→0。

根据式(8)和(9)组成的航天器姿态误差动力学方程可知，此时该系统是一个标准的级联系统，因此可采用反步法进行姿态控制器设计。为此引入如下的变量变换:

z1=σe

(10)

(11)

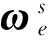
Step1 选取正定的Lyapunov函数

(12)

则式(12)两边同时对时间t求导得

(13)

此时选取虚拟控制输入

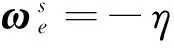
(14)

式中，η为正常数，且非线性函数φ(σe)为

φ(σe)=αarctan(βσe)

(15)

α与β的选取原则是使非线性函数φ(·)尽可能的接近符号函数的性质，本文一律选择α=0.65，β=8。

由式(14)可得

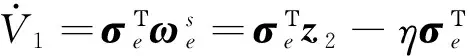
(16)

而有σe将渐近收敛至0。

Step2 考虑到系统惯量的不确定性，文中涉及自适应控制律，首先对式(11)求时间的导数

(17)

结合式(14)和(15)，得

(18)

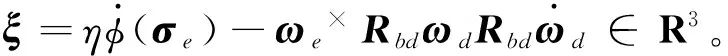
整理式(18)，得

(19)

其中，Θ为航天器的惯量参数，Θ=[J11J22J33

J12J13J23]Τ。

(20)

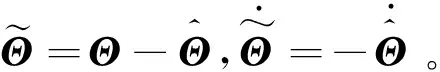
针对航天器动力学系统式(6)，选取如下Lyapunov函数：

(21)

结合式(8)，(9)和(17)，

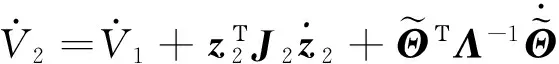
(22)

此时设计如下控制器：

(23)

其中，ζ为正常数。

将式(23)带入式(22)，得

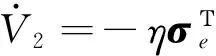
(24)

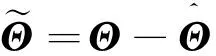
3 数字仿真验证

以HEO卫星与GEO目标交会观测期间的随动指向为背景，验证方法的有效性，轨道根数如表1。

初始姿态指向偏差为[0 10° 0]，角速度偏差为[0 0 0] ((°)/s)。卫星的转动惯量为

卫星俯仰轴方向安装2块大型太阳翼，考虑柔性帆板的前6阶模态，阻尼比ζi=0.005。

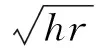
由图1可知，交会过程是一个目标由远及近，在过顶时相对距离最近大约50km，距离再逐步增大的过程。

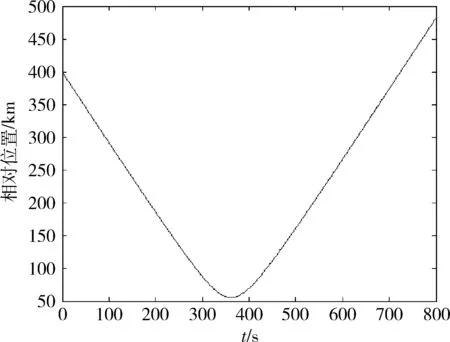
图1 相对位置变化曲线

初始相对位置和速度误差为[10 10 10]km，[0.1 0.1 0.1]km/s，相对导航设备测量误差为10＂。采用提出的相对导航方法对相对位置进行实时估计，并进一步计算期望姿态，得到的期望姿态精度达到0.01°和0.002(°)/s。假设地面对非合作目标测轨精度为5km，通过轨道预报得到的期望姿态精度为1.5°和0.12(°)/s，与相对测量相比，差2个数量级。

图2和4为根据相对测量得到的追踪星的期望姿态、期望角速度和期望角加速度变化曲线，可见跟踪角速度需求最高为1.1(°)/s，角加速度为0.015(°)/s2。

图2 期望姿态变化曲线

图3 期望角速度变化曲线

图4 期望角加速度变化曲线

为满足姿态机动要求，采用五棱锥构型的SGCMGs作为执行机构，初始框架角、角速度均为0，单个CMG的最大角动量为500N·m·s，最大输出力矩为200N·m，操纵律选用带零运动的鲁棒伪逆操纵律[14]。

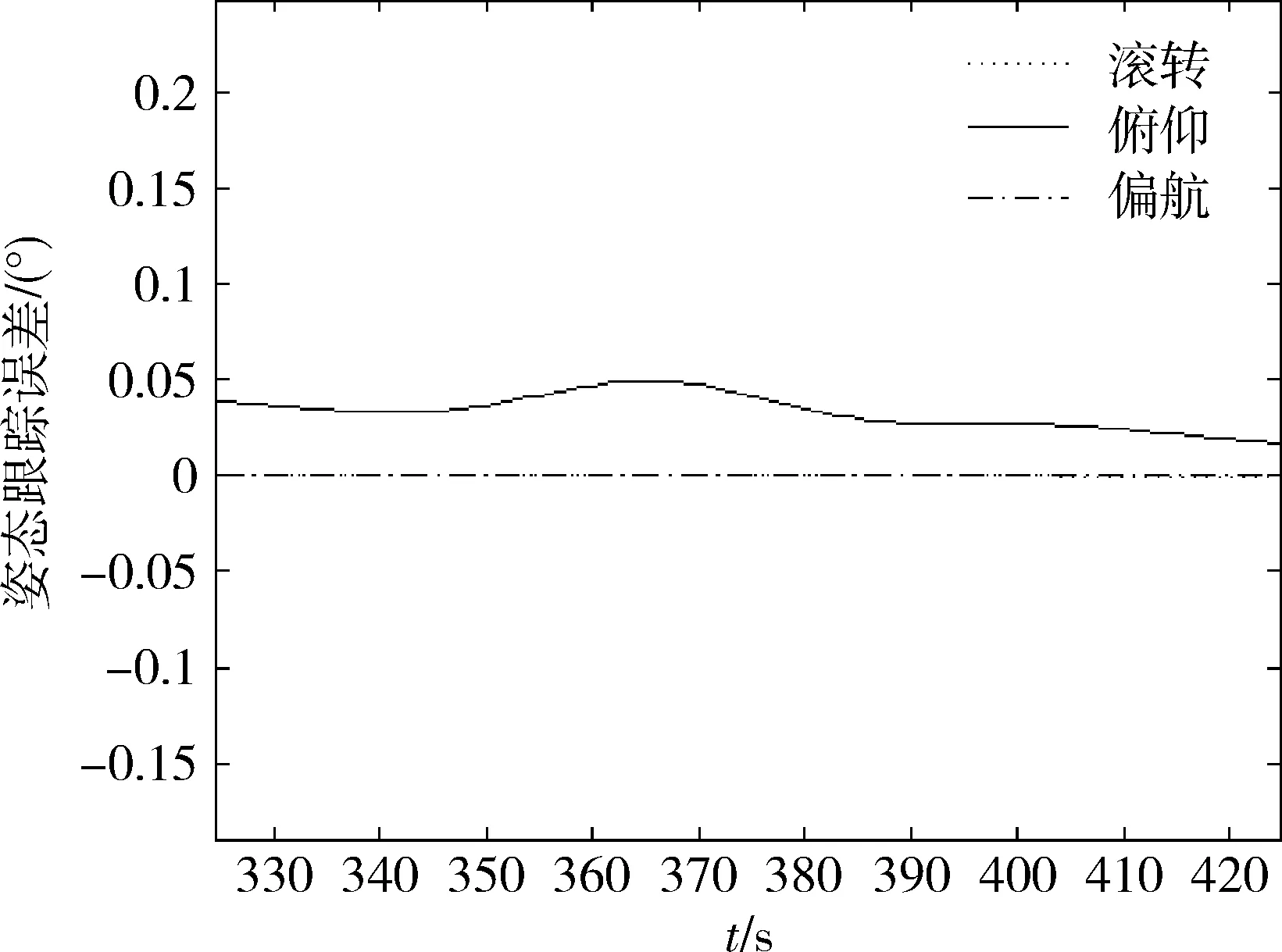
图5 姿态跟踪误差变化曲线

图6 姿态角速度跟踪误差变化曲线

从图5和6中可以看出追踪星能实现对目标的持续稳定跟踪，在过顶前后的跟踪精度小于0.05°，跟踪稳定度小于0.006(°)/s。以上结果证明了所提方法的有效性。

4 结论

研究了大型挠性航天器对非合作目标随动指向控制问题。采用平方根容积卡尔曼滤波进行相对位置估计，进一步计算了期望姿态，精度达到0.01°。考虑系统惯量不确定性，采用反步自适应控制律进行姿态跟踪，在考虑执行机构和敏感器误差的情况下跟踪精度达到0.05°。

参 考 文 献

[1] 董天舒, 何英姿. 基于增益分配的航天器高精度指向跟踪控制[J]. 航天控制, 2016, 34(1):50-56.(DongTianshu,HeYingzi.AHighPrecisionAttitudePointingTrackingControlforSpacecraftBasedontheGainSchedule[J].AerospaceControl，2016, 34(1):50-56.)

[2] 张庆展, 靳永强, 康志宇, 肖余之. 挠性航天器掠飞观测目标时的建模与控制[J]. 空间科学学报, 2015, 35(6):738-746. (ZhangQingzhan,JinYongqiang,KangZhiyu,XiaoYuzhi.ModelingandControlStrategyforaFlexibleSpacecraftwhenItEncountersandObservestheTarget[J].Chin.J.SpaceSci., 2015, 35(6): 738-746.)

[3] 李化义, 张迎春, 等. 与非合作目标编队的相对姿态控制[J]. 宇航学报, 2007, 28(5): 1210-1214. (LiHuayi,ZhangYingchun,etal.RelativeAttitudeControlinNon-cooperativeTargetFormationFlying[J].JournalofAstronautics, 2007, 28(5): 1210-1214.)

[4] 宋申民, 张保群, 陈兴林. 空间绕飞任务中航天器姿态跟踪的鲁棒控制[J]. 系统工程与电子技术, 2011, 33(1):120-126. (SongShenmin,ZhangBaoqun,ChenXinglin.RobustControlofSpacecraftAttitudeTrackingforSpaceFly-aroudMisson[J].Sys.Eng.Elec., 2011, 33(1): 120-126.)

[5]ZhuZL,YanY.Space-basedLine-of-sightTrackingControlofGEOTargetUsingNonsingularTerminalSlidingMode[J].AdvancesinSpaceResearch, 2014, 54: 1064-1076.

[6]HablaniHB.DesignofaPayloadPointingControlSystemforTrackingMovingObjects[J].JounalofGuidance,ControlandDynamics, 1989,12(3): 365-374.

[7]HablaniHB.MultiaxisTrackingandAttitude-controlofFlexibleSpacecraftwithRectionJets[J].JounalofGuidance,ControlandDynamics, 1994,17(4): 831-839.

[8] 徐帷, 武海雷, 卢山,等. 大椭圆轨道卫星交会高轨目标的高精度视线跟踪控制[J]. 空间控制技术与应用, 2015, 41(2):6-11. (XuWei,WuHailei,LuShan,etal.AHighPrecisionAttitudeTrackingControlMethodforHighlyEccentricOrbitSpacecraftRendezvouswithaHEOTarget[J].AerospaceControl&Application, 2015,4(2):6-11. )

[9] 宋斌, 颜根廷, 李波,等. 基于自抗扰技术的挠性航天器高精度指向控制[J]. 上海航天, 2014, 31(2):1-7.(SongBin,YanGenting,LiBo,etal.ActiveDisturbanceRejectionControlforFlexibleSpacecraftHigh-AccuracyAttitudePointing[J].AerospaceShanghai, 2014,31(2):1-7.)

[10]KaufmanE,LovellTA,LeeT.NonlinearObservabilityforRelativeOrbitDeterminationwithAngles-OnlyMeasurements[J].JournaloftheAstronauticalSciences, 2016, 63:1-21.

[11]LenkaranA,SimonH.CubatureKalmanFilters[J].IEEETransactionsonAutomaticControl, 2009,54(6):1254-1269.

[12] 金磊, 徐世杰. 采用单框架控制力矩陀螺和动量轮的航天器姿态跟踪控制研究[J]. 宇航学报, 2008, 29(3): 916-921. (JinLei,XuShije.AttitudeTrackingControlofaControlMomentGyrosSpacecraftUsingSingleGimbalandMomentumWheels[J].JournalofAstronautics, 2008, 29(3): 916-921.)

[13] 马广富, 张海博, 胡庆雷. 基于反步法的主从航天器相对姿态控制[J]. 控制理论与应用, 2012, 29(6):797-802. (MaGuangfu,ZhangHaibo,HuQinglei.Backstepping-basedRelative-attitudeControlfortheLeader-followerSpacecrafts[J].ControlTheory&Applications, 2012, 29(6):797-802.)

[14] 章仁为.卫星轨道姿态动力学与控制[M].北京：北京航空航天大学出版社, 1998:157-176.

Research on Attitude Pointing Tracking Control for Spacecraft Based on Relative Orbit Measurement

Xu Guangde，Yan Xin，Gou Zhongqiu， Zhang Bainan

Institute of Manned Space System Engineering, China Academy of Space Technology, Beijing 100194,China

Theproblemofpointingtrackingcontroloflargeflexiblespacecraftsisinvestigatedinthepaper.Anestimationmethodofdesiredattitudeandanattitudecontrolmethodbasedonthebacksteppingtechniquearedeveloped.Amethodforrelativeorbitdeterminationbasedonroot-squarecubatureKalmanfiterisproposed.Thedesiredattitudeofthechasersatellitetoalignitsobservationaxistothetargetiscalculatedwiththeestimatedpositionandvelocity.Anadaptivebacksteppingattitudecontrollerissynthesizedforthechasersatellitewithunknowninertiamatrix,whichisbasedonthechaserattitudeerrordynamicmodelrepresentedbymodifiedRodriguesparameters(MRP).Thesimulationresultsshowtheeffectivenessandfeasibilityoftheproposedmethodduringtheapplicationtosapceobservation.

Relativemeasurement;Attitudetracking;Backsteppingmethod; SGCMGs

2016-08-22

徐广德(1990-)，男，山东菏泽人，博士研究生，主要研究方向为航天器动力学与控制；闫 鑫(1984-)，男，河南周口人，博士，工程师，主要研究方向为导航、制导与控制；苟仲秋(1980-)，男，河南孟州人，博士，高级工程师，主要研究方向为航天器总体设计；张柏楠(1962-)，男，黑龙江齐齐哈尔人，硕士，研究员，主要研究方向为航天器总体设计。

V448.2

A

1006-3242(2017)01-0054-06