基于人工蜂群算法的直流双闭环PID电机调速系统研究*

徐 建 黄 华 董杰楚 廖红华

1.湖北民族学院科技学院，湖北恩施 4450002.四川大学电气信息学院，四川成都 610065



基于人工蜂群算法的直流双闭环PID电机调速系统研究*

徐 建1,2黄 华2董杰楚1廖红华1

1.湖北民族学院科技学院，湖北恩施 4450002.四川大学电气信息学院，四川成都 610065

以直流双闭环模型为基础，针对现行直流双闭环PID控制器参数整定与优化的困难，通过将人工蜂群算法引入直流双闭环调速系统，实现直流电机调速及其PID控制器参数的自整定，采用系统的阶跃响应等对人工蜂群算法的优化结果进行对比分析，表明改进的人工蜂群算法比传统工程设计法能获得更好的动态性能指标，以及更快的跟随性与鲁棒性，为PID参数优化提供了一个综合性较好的实用方法。

人工蜂群算法；直流电机双闭环；PID控制；参数优化

直流双闭环调速系统在理论和实践上都比较成熟，是一种常见的调速控制系统，目前广泛应用于工业控制中，其具有良好的起、制动性能，易于在大范围内平滑调速，且调速后的效率较高。针对直流双闭环PID控制器参数整定与优化的问题，国内外学者已做了很多研究，但大部分研究都集中在控制器内部结构[1]。针对直流双闭环调速系统时变性和不确定性，本文通过将人工蜂群算法引入直流双闭环调速系统，实现直流电机调速及其PID控制器参数的自整定与优化，通过系统仿真可以看出，改进的人工蜂群算法比传统工程设计法性能指标更好，可以广泛应用于双闭环调速系统中。

1 直流电机双闭环控制系统仿真

此仿真实例来自文献[2]，在三相桥式晶闸管整流装置控制双闭环调速系统中，直流电动机的相关参数：UN=220V，IN=136A，nN=1460r/min，电动机的电动势系数Ce=0.132Vmin/r，允许过载的倍数λ=1.5，电枢回路的总电阻R=0.5Ω，晶闸管装置的放大系数Ks=40，电枢回路电磁时间常数Tl=0.03s，电力拖动系统机电时间常数Tm=0.18s，电流的反馈系数β=0.05V/A，转速的反馈系数α=0.005Vmin/r。通过仿真计算可知：Ckp=0.5067，CKi=16.89，SKp=11.7，SKi=134.48。Ckp和Cki为电流环的PI参数，Skp和Ski为转速环的PI参数。Simulink模块如图1，其中step为给定转速输入，step2为负载电流Id阶跃；out1，out2分别为转速和电流环输出数据到workspace的端口。

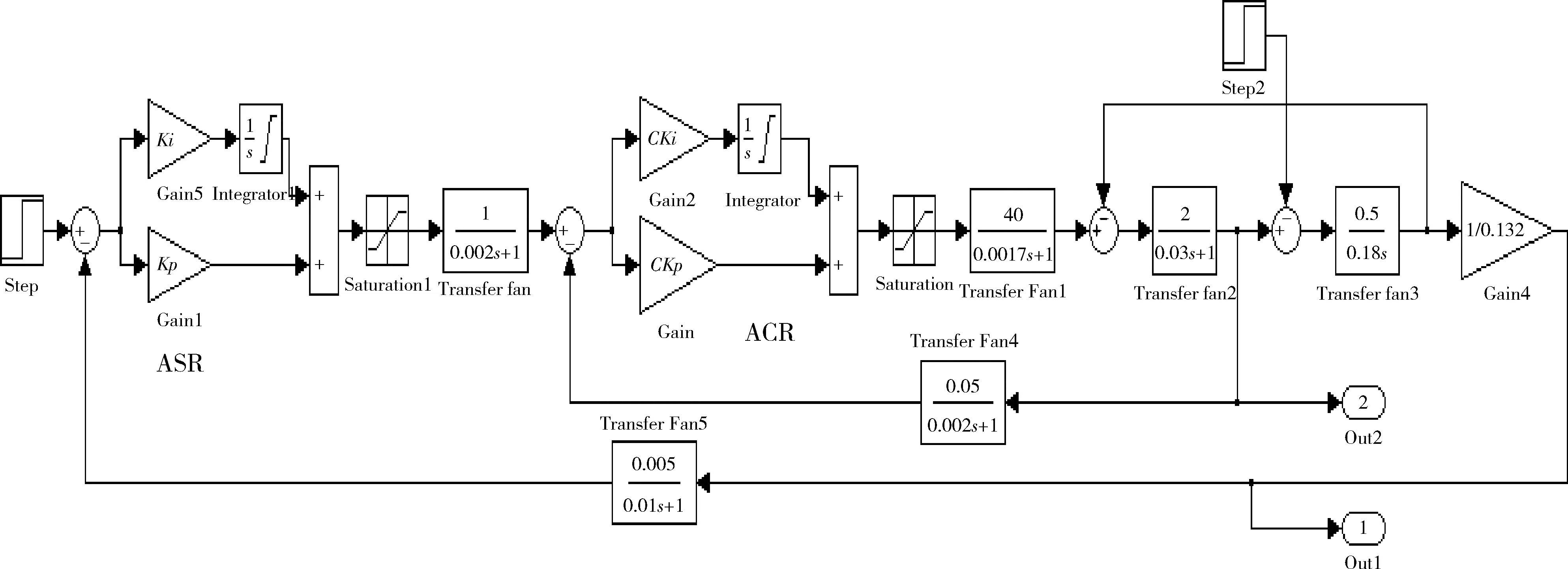
图1 直流双闭环PID调速系统

2 人工蜂群算法优化双闭环PI参数的实现

传统的直流电机双闭环调速系统中的ASR和ACR一般使用结构简单、性能可靠的带限幅PI调节器。在实际生产现场，由于种种原因，比如控制系统的抽象传递函数和实际有偏差，电机是一个非线性模型，很多拖动带载也含有间隙或弹性等非线性扰动，使得控制器的参数设计往往难以达到最优[2-3]。因此本文采用基于生物模型的蜂群算法对双闭环的PI参数进行整定。用人工蜂群算法进行PI控制器参数的整定，即找出参数θ：

θ={SKp，SKi，CKp，CKi}

(1)

其中，SKp，SKi为ASR环PI参数，CKp和CKi为ACR环PI参数，使控制系统的动态过程指标满足要求，其实质是转化为基于一定目标适应函数进行函数寻优的问题。蜂群算法为script代码，在运行中通过调用直流双闭环的Simulink模块得到out1和out2的输出，将此输出作为ABC算法的适应度评估的输入。蜂群算法通过修改SKp，SKi，CKp和CKi参数的值获取不同的输出响应，评估这些响应值来判断输入参数的优劣[4]。

适应度函数的选择是算法最核心的部分，为使电机转速环及电流环具有快速、平稳和超调量小的目标，使用ITAE作为系统性能评价指标。相对应的适应度函数为[5]：

(2)

式中，0～ta为空载启动时间段，tb～tc为加载时间段。s为转速环的最大超调量。α，β，γ为3个权重系数，调节这3个参数可以控制性能指标的倾向。本文选择α=0.6，β=0.4，γ=2.0。es(t)和ec(t)分别为按照额定转速和额定电流归一化后的速度误差和电流误差。在归一化中，转速环额定转速设为1500r/min。电流环由于受到斜坡反电动势的扰动而存在静差，设计电流环的最大电流为200A，但是在恒流升速阶段因为静差的存在电流值并不能达到200A，于是将空载启动过程中的额定电流定为190A，加载过程的额定电流为负载电流。本文在启动过程中加载的电流为100A，即tb～tc时间段内的额定电流值为100A[6]。

为了观察算法的稳定性，仿真时进行了30次(每一次运行执行60代)算法的执行，从中挑出最终全局适应度居中的参数值。最终30次试验全部找到了使系统稳定运行的参数，挑出适应度居中对应的参数为：Ckp= 1.9419，CKi=17.5172，SKp=36.7219，SKi=643.7838。算法优化过程中的适应度变化如图2(数值放大1000倍，便于观察适应度变化趋势)所示，y轴是ITAE指标下速度与电流的和值，用于评价系统的优良程度，越小性能越好，x轴为优化算法的代数。从图2可看出，人工蜂群算法具有优秀的寻优能力，在整个算法运行过程中一直保持着寻优能力，没有在某一个极值点处逗留过长的时间。本文只是使用60代的优化次数来优化PI控制器参数，按照目前的趋势看算法并没有陷入到某个点，如果设置更多的优化代数蜂群算法将有更好的表现，只是会因此增加优化时间。

图2 适应度变化趋势图

3 转速环和电流环的对比仿真

空载下的启动响应反应了控制器最原始的设计性能，为了比较非理想空载启动下的响应，在启动过程加入负载电流为100A的负载启动，对应带载启动转速响应如图3所示。对应带载启动电流环响应如图4所示。

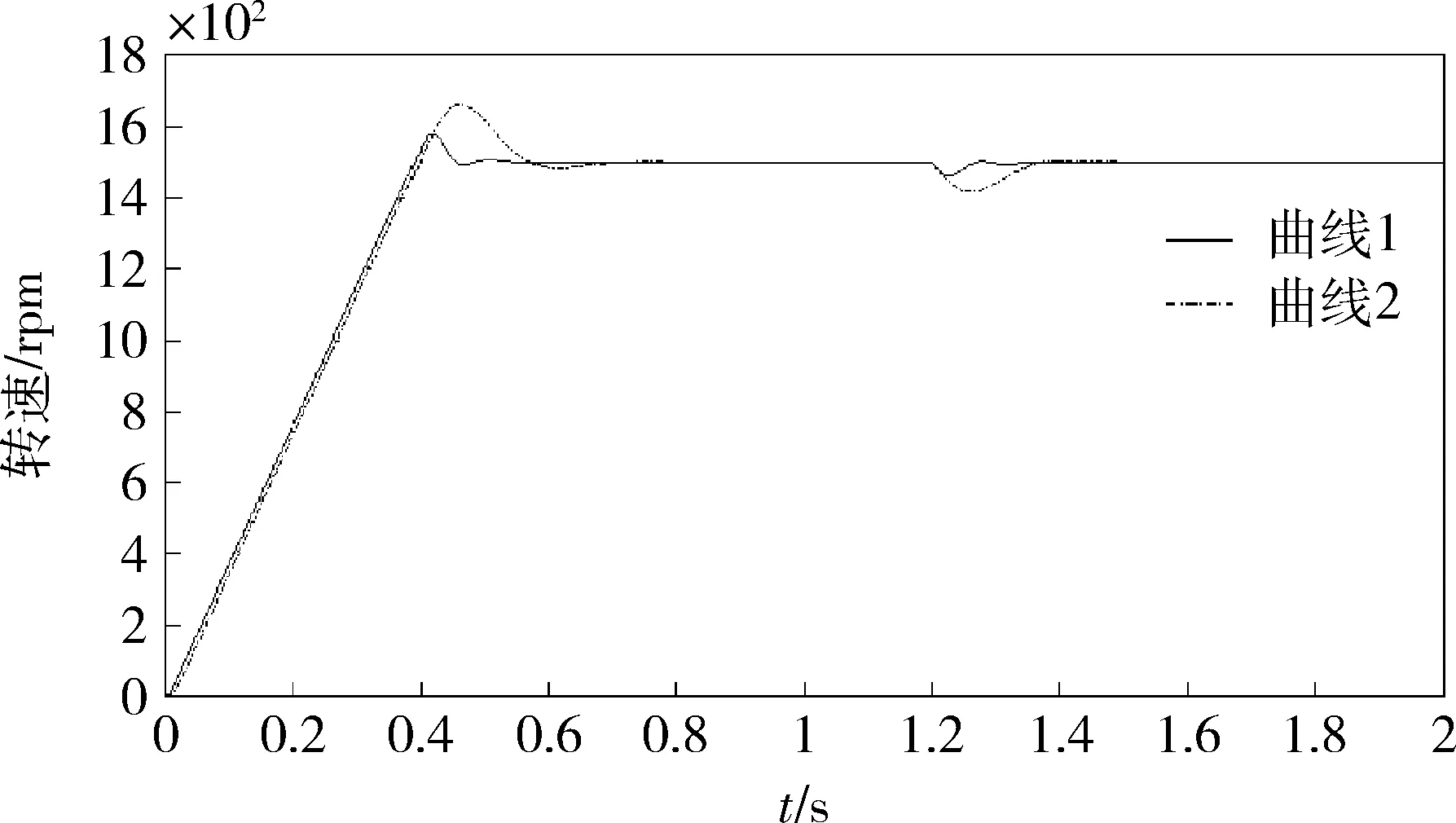
图3 带载启动转速环响应

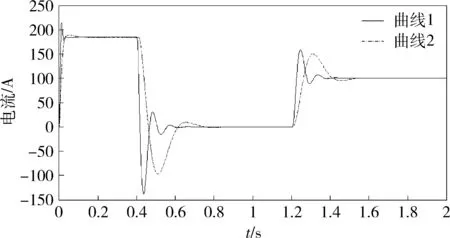
图4 带载启动电流环响应

在图3和4中，曲线1为工程设计方法设计调节器的响应曲线，曲线2为蜂群算法优化控制器的响应曲线。从图3可看出，加载情况下可以有效缓解速度环超调的问题，经过优化后的控制器的稳定速度和超调量好于传统控制器。2种控制器的电流环在电流升到最大值过程中的稳定过渡时间一样，但在0.5s时优化过的控制器在响应速度方面优于传统控制器。加载后系统升速到额定转速的时间变长，和理论分析一致[7]。

为了分析比较2种参数的稳定性，先让转速空载达到额定转速，然后加入负载，比较2种控制器的稳定性，如图5和6所示。

图5 转速环加载的响应

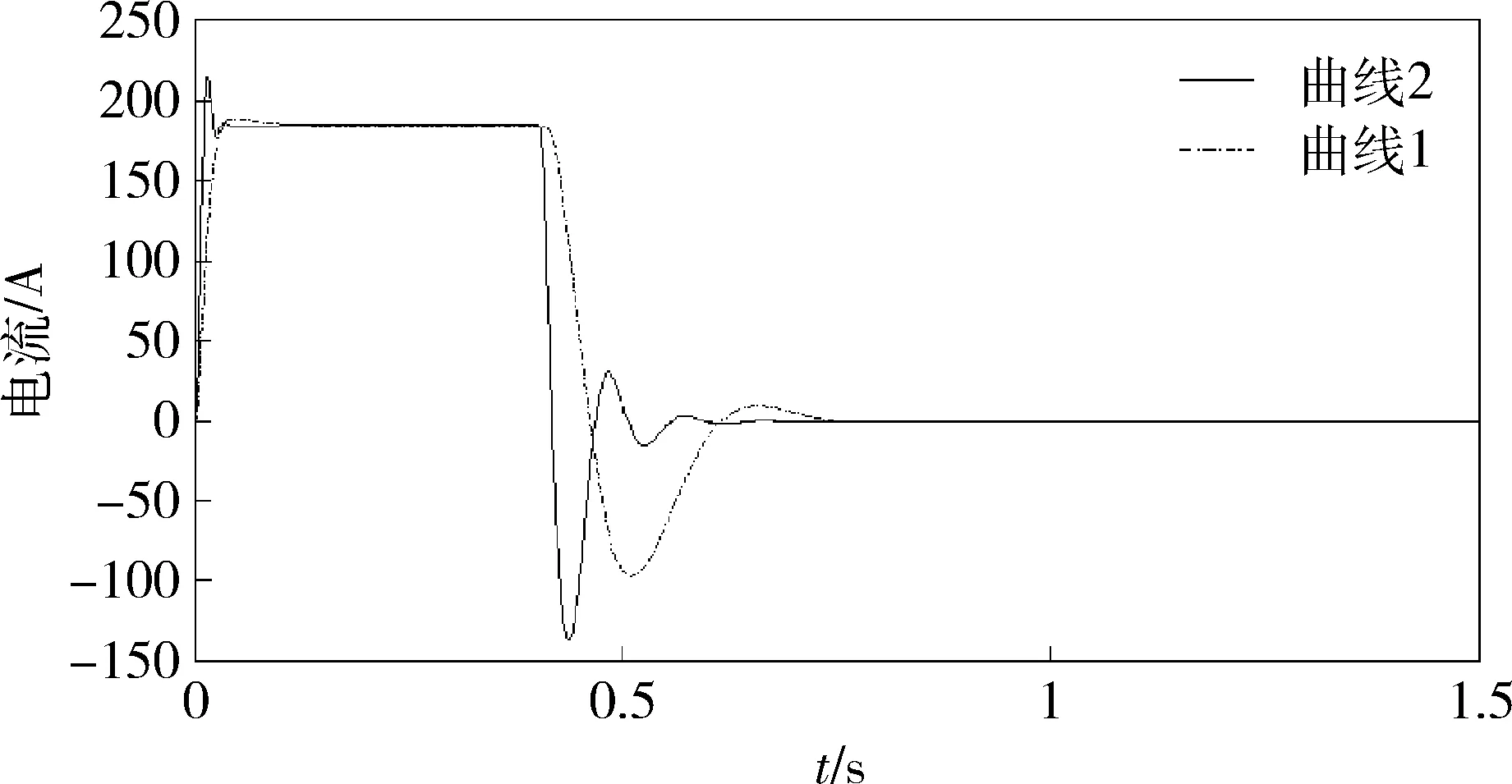
图6 电流环加载的响应

图5和6中，曲线1为用工程设计方法设计调节器的响应曲线，曲线2为用蜂群算法优化控制器的响应曲线，在1.2s时加入100A的负载，由图5转速环的响应曲线对比可明显看出，蜂群优化控制器抗扰性能好。相应的电流环情况如图6所示，蜂群优化调节器与传统设计调节器比较，蜂群优化控制器输出响应迅捷，稳定性能优良[8]。

4 总结

根据MATLAB仿真结果可以得到： 1)在阶跃响应的动态性能上，经蜂群算法优化的控制器响应速度更快，具有更优秀的阶跃响应能力；2)在稳定性方面，蜂群算法优化的PI控制器明显优于工程设计的PI控制器；3)在控制器的设计方面，构建较好适应度评价函数后，使用蜂群算法可在不知道控制系统具体参数的情况下设计出理想的控制参数。通过以上分析，可以得出采用蜂群算法优化过的双闭环控制器可以较好地改进传统PID控制器的不足，提高控制效果。

[1] 郑光，王迄冉．双闭环直流调速系统优化及仿真研究[J]．计算机仿真，2013，30(7)：321-325．(Zheng Guang，Wang Yiran．Simulation and Optimization of Parameters of Double Closed -Loop DC Speed Tuning System[J]．Computer Simulation，2013，30(7)：321-325．)

[2] 阮毅，陈伯时．电力拖动自动控制系统．第4版[M]．北京：机械工业出版社，2009：79-89．(Ruan Yi，Chen Boshi．Automatic Control Systems of Electric Drives．The fourth edition [M]．Beijing：China Machine Press，2009：79-89．)

[3] 王云良，王继水，王敏其．无刷直流电机自适应模糊优化控制[J]．电机控制与应用，2014，41(11)：14-17．(Wang Yunliang，Wang Jishui，Wang Minqi．Adaptive Fuzzy Control of Speed Regulating for BLDCM Based on Optimization Algorithm[J]．Electric Machines & Control Application，2014，41(11)：14-17．)

[4] 胡伟，徐福缘．基于改进粒子群算法的 PID 控制器参数自整定[J]．计算机应用研究，2012，29(5)：1791-1794．(Hu Wei1，Xu Fuyuan．Self-tuning of PID Parameters Based on Improved Particle Swarm Optimization[J]．Application Research of Computers，2012，29(5)：1791-1794．)

[5] 张冬丽，唐英干，关新平．用改进的人工蜂群算法设计AVR系统最优分数阶PID控制器[J]．自动化学报，2014，40(5)：973-980．(Zhang Dongli．Tang Yinggan．Guang Xinping．Optimum Design of Fractional Order PID Controller for an AVR System Using an Improved Articial Bee Colony Algorithm[J]．Acta Automatica Sinica，2014，40(5)：973-980．)

[6] 吴燕翔，张朝君，周超群．基于参数自整定模糊 PID 双闭环直流调速系统的设计仿真[J]．化工自动化及仪表，2013，40(2)：136-139．(Wu Yanxiang，Zhang Chaojun，Zhou Chaoqun．Design and Simulation of Double Closed Loop DC System Based on Parameter Self-tuning Fuzzy PID[J]．Control and Instruments in Chemical Industry，2013，40(2)：136-139．)

[7] 朱志强，江紫亚，何玉庆．PID 控制器的频域特性与无模型参数调节[J]．控制与决策，2014，29(10)：1833-1838．(Zhu Zhiqiang，Jiang Ziya，He Yuqing．Frequency Properties of PID Controller and Model Free Tuning[J]．Control and Decision，2014，29(10)：1833-1838．)

[8] 张厚升，李素玲，于兰兰，等．基于 MATLAB 的双闭环直流调速系统设计与仿真分析[J]．山东理工大学学报(自然科学版)，2013，27(4)：49-53．(Zhang Housheng，Li Suling，Yu Lanlan，et al．The Design and Simulation Analysis of Double Closed Loop DC Motor Control System Based on MATLAB[J]．Journal of Shandong University of Technology(Natural Science Edition)，2013，27(4)：49-53．)

征 文 通 知

智能控制技术是自动控制技术发展的必然趋势，智能控制已在模式识别、决策支持、过程控制、故障诊断、预测建模等许多科学与工程领域得到了成功应用，它的应用已经或将给工业制造体系和人们的生活方式带来颠覆性变化。

为了交流智能控制技术新成果，促进这一学科领域的创新与发展，增强科技人员之间的交流与合作，宇航智能控制技术实验室、北京航天自动控制研究所和《航天控制》编辑部拟定于2017年下半年联合举办“智能自主控制技术”学术研讨会。现将有关事项通知如下：

一、征文范围

1.人工智能与仿生科学

2.智能传感器与智能感知

3.智能计算与智能控制

4.智能规划、决策与指挥

5.航天智能自主系统

二、论文要求

1.应征论文内容必须紧扣本次研讨会的征文范围，强调针对性、创新性、前瞻性。

2.论文字数不超过6000字(包括摘要、图表)，用A4标准纸打印，不超过6页。上边距：2.5cm，下边距：2.5cm，左右边距：2.5cm。正文行距均设为最小值16磅；一级题目为黑体，四号，且段前段后设为6磅；二、三级标题同正文。

3.文章应包括：文章题目(黑体二号，居中)；作者姓名(宋体四号，居中)；作者单位、地址、邮政编码(宋体，五号，居中)；摘要(摘要为黑体五号，内容为楷体五号)；关键词(关键词为黑体五号，内容为楷体五号)；正文(宋体，五号)；参考文献(宋体，小五号；应为公开发表的最新文献)；作者简介(宋体，五号；应包括性别、出生年月、职称、专业和研究方向、通信地址、邮编以及E-mail地址、联系电话等)。

三、投稿方式：

网上投稿，网址为http://htkz.cn。来稿须保证内容真实、未侵犯他人知识产权、无泄密，作者署名无争议，未一稿多投。来稿须经过保密审查，勿投寄涉密稿件，邮寄纸质保密审查单。稿件请用WORD格式，请务必在文章标题后面写上“(征文投稿)”。

四、截稿日期

征文截止日期: 2017年5月30日

录用通知日期: 2017年6月30日

五、联系方式

联系电话：(010)68388585；68762264

联系人：杨 柳

通信地址: 北京142信箱402分箱《航天控制》编辑部

邮 编：100854

主办单位: 宇航智能控制技术国家级重点实验

2017年 2月

Research on DC Double Closed-Loop PID Motor Speed-Regulation System Based on Artificial Bee Colony Algorithm

Xu Jian1,2, Huang Hua2, Dong Jiechu1, Liao Honghua1

1.Science and Technology College of Hubei University for Nationalities, Enshi 445000,China2. School of Electrical Engineering and Information, Sichuan University , Chengdu 610065, China

Basedonthedoubleclosed-loopDCmodel,aimingatthedifficultyofcurrentDCdoubleclosed-loopPIDcontrollerparameterstuningandoptimization，accordingtotheartificialbeecolonyalgorithmwhichisintroducedintotheDCdoubleclosed-loopspeedregulationsystem,theDCmotorspeedandparametersofPIDcontrollerisrealizedandtheoptimalresultsofartificialbeecolonyalgorithmiscomparedandanalyzedbyusingthestepresponseofthesystem.Theresultsshowthatthedynamic-performance-index-improvedartificialbeecolonyalgorithmcanobtainbetterperformancethanthetraditionaldesignmethodandisfollowedfasterandrobust,Thus,abetteroverallperformanceandpracticalmethodisproposedforPIDparameteroptimization.

Artificialbeecolony(ABC)；DoubleloopDCmotor(DLM)；PIDcontrol；Parameteroptimization

*国家自然科学基金(61263030)；湖北民族学院科技学院科研项目(KJB201602)

2016-05-13

徐 建(1981-)，男，湖北英山人，博士研究生，讲师，主要从事嵌入式与智能控制方面的研究；黄 华(1961-)，男，成都人，博士，教授，主要从事信号处理与自动控制方面的研究；董杰楚(1987-)，男，湖北恩施人，工程师，主要从事电气自动化方面的研究；廖红华(1972-)，男，湖北恩施人，博士，教授，主要从事信号检测与自动控制方面的研究。

TP181

A

1006-3242(2017)01-0092-04