一道定点调考题的解法与推广探究

湖北省阳新县高级中学(435200) 邹生书

一道定点调考题的解法与推广探究

湖北省阳新县高级中学(435200) 邹生书

题目在平面直角坐标系中,设A,B,C三点是曲线上三个不同的点,且D,E,F分别是BC,CA,AB的中点,则过D,E,F三点的圆一定经过定点____.

这是湖北省武汉市2017届高三2月调考数学理科第15题,题意简明易懂,试题能力立意,综合考查数学思想方法和推理探究能力,考查对问题的整体掌控能力和直觉思维能力,考查创新意识、数学综合素质和数学素养.下面介绍笔者对这道定点调考题的解法与问题的推广探究历程,与读者分享.

1.化归转化退步求解

华罗庚先生曾指出:“善于退,足够的退,退到最原始而不失重要的地方,是学好数学的一个诀窍.”这里所说的“退”,其含义很丰富,包含从特殊退到特殊、从一般退到特殊和从特殊退到一般三种情形.所谓从特殊退到特殊,就是将一种特殊的情形退到另一种更为特殊的情形去研究;所谓从一般退到特殊,指的是运用特例法对问题的一般情形做出判断;所谓从特殊退到一般,指的是把问题放在一个一般的背景中去思考.

问题在平面直角坐标系中,设A,B,C三点是曲线上三个不同的点,且D,E,F分别是BC,CA,AB的中点,则过D,E,F三点的圆一定经过定点____.

2.合情推理探求定点

分析一方面,注意到的图象是双曲线,两条坐标轴是它的对称轴,坐标原点是它的对称中心,因此解题时应充分利用图象的对称性.另一方面,题目告诉我们过D,E,F三点的圆一定经过定点,但没有说是几个定点,因此,首先要对定点个数作出判断.显然外接圆不可能过三过定点,假若过三个定点,则这些圆是同一个圆,这不可能.假若过两个定点,那么这些圆的圆心在以这两个定点为端点的线段的垂直平分线上,这也不可能.故外接圆只过一个定点.当然上面的推理用的是直觉思维,并非逻辑推理.基于上述两点有如下几种解法.

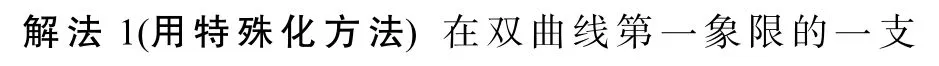
因为双曲线关于原点对称,则A,B,C三点关于原点的对称点A′,B′,C′在双曲线的另一支上,设D′,E′,F′分别是边B′C′,C′A′,A′B′的中点,由中心对称知△D′E′F′的外接圆方程为

解方程①②得唯一解x=0,y=0,即原点是两个圆的唯一公共点,故所求定点为原点.

点评上述解法需要解方程组有一定的运算量,下面我们改进上述解法,采用方程思想进行定性分析的方法求解.

解法2(用方程思想)设A,B,C是双曲线在第一象限的一支上的任意三点,设过D,E,F三点的圆的方程为

因为双曲线关于原点对称,则A,B,C三点关于原点的对称点A′,B′,C′在双曲线的另一支上,设D′,E′,F′分别是边B′C′,C′A′,A′B′的中点,由中心对称知△D′E′F′的外接圆方程为

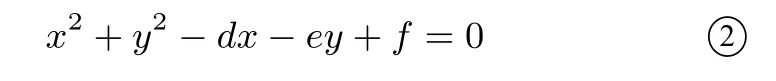
依题意这两个圆过同一定点,所以方程组①②有解.两方程相减得

则

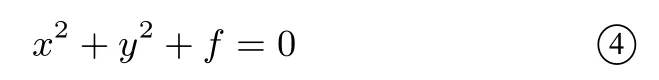
若f＞0,则方程组无解,从而两圆没有公共点,不合题意.若f＜0,则由方程③④知方程组有两个解,但两个解不是定值,即两圆有两个不是定点的公共点,不合题意.若f=0,则方程组有唯一而确定的解x=0,y=0,符合题意.故所求定点为原点.

解法3(根据轴对称性进行合情推理)因为两条坐标轴是双曲线的对称轴,设A,B,C三点关于x轴的对称点分别为A′,B′,C′,设D′,E′,F′分别是边B′C′,C′A′,A′B′的中点,则△DEF的外接圆与△D′E′F′的外接圆也关于x轴对称.因为这两个圆经过同一定点,所以定点一定在x轴上,同理定点也在y轴上,所以定点就是两坐标轴的交点即坐标原点O.

解法4(根据中心对称性进行合情推理)因为坐标原点是双曲线的对称中心,设A,B,C三点关于原点的对称点分别为A′,B′,C′,设D′,E′,F′分别是边B′C′,C′A′,A′B′的中点,则△DEF的外接圆与△D′E′F′的外接圆也关于原点对称.因为这两个圆都只经过同一定点,所以定点只能是坐标原点O.

根据以上分析和合情推理,我们不难求出调考题所求的定点坐标为(1,0).

3.演绎推理证明推广

下面我们将问题一般化并将方程标准化可得如下结论:

性质1 在平面直角坐标系中,设A,B,C三点是等轴双曲线xy=λ(λ＞0)上三个不同的点,且D,E,F分别是BC,CA,AB的中点,证明过D,E,F三点的圆必过坐标原点O.

证法1(证四边形OFDE的一组对角互补)因为A,B,C三点是等轴双曲线xy=λ上三个不同的点,故可设A,B,C三点与双曲线有如下两种位置关系:一是三点均在同一支上,如图1;二是其中一个点在一支上,另两个点在另一支上,如图2.

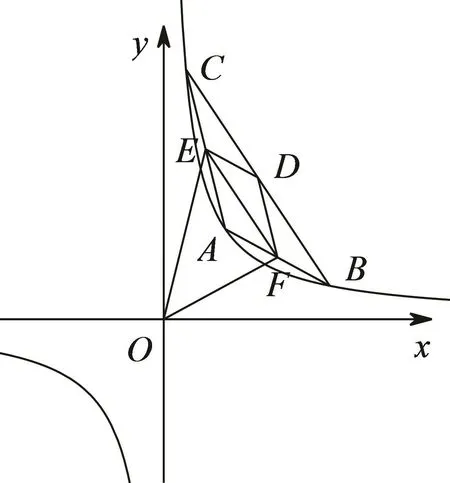
图1

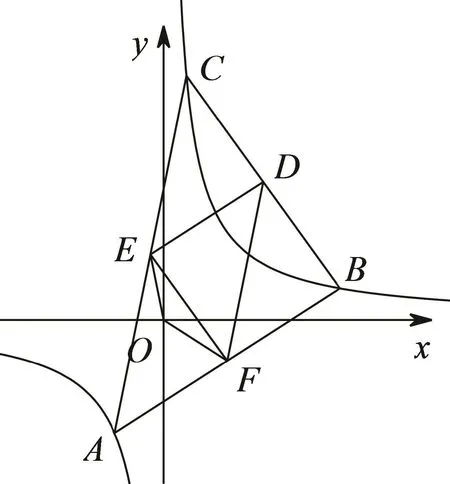
图2

要证△ABC各边的中点△DEF的外接圆过原点O,只需证O,D,E,F四点共圆,只需证∠EOF+∠EDF=180°.易知EAFD是平行四边形,所以∠EDF= ∠BAC,故只需证 ∠EOF+ ∠BAC=180°,只需证 tan∠EOF=−tan∠BAC.

综上,tan∠EOF=−tan∠BAC.故O,D,E,F四点共圆,则过D,E,F三点的圆经过定点,这个定点就是坐标原点也就是等轴双曲线的对称中心.

同理,边OD与边OF的垂直平分线的交点坐标与点M相同,即它们也相交于同一点M.由线段垂直平分线的性质得MO=MD=ME=MF,故O,D,E,F四点在以点M为圆心的圆上,所以过D,E,F三点的圆必经过点O.

由曲线平移的知识可得如下一般性结论:

性质2 在平面直角坐标系中,设A,B,C三点是曲线

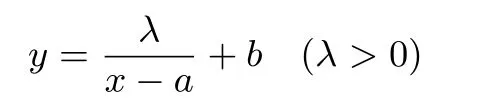
上三个不同的点,且D,E,F分别是BC,CA,AB的中点,则过D,E,F三点的圆必过曲线的对称中心即定点(a,b).

等轴双曲线的上述性质用文字语言表达如下:

性质等轴双曲线上任意三点所构成的三角形的中点三角形的外接圆必过双曲线的中心.

笔者借助几何画板研究发现,上述性质是等轴双曲线的一个特有性质,并非所有的双曲线所拥有.

通俗地说,合情推理是一种“合乎情理”的推理,在上述研究中,我们用合情推理猜测出“如果定点存在,则定点只能是一个并且是等轴双曲线的对称中心”,这一猜测为我们用四点共圆的方法来证明命题提供了证明的思路和方向.演绎推理是证明数学结论、建立数学体系的重要思维过程,但数学结论、证明思路等的发现,主要靠合情推理.合情推理和演绎推理是思维的两个不可缺失的方面,两者相辅相成、相得益彰.数学的教学是思维的教学,在课堂教学中,我们不仅要教会学生学会证明,也要教会学生学会猜想.