关于新课程背景下初中数学教学方法的优化

姚杰

【摘要】新课程改革的深入推進使教学工作面临新的改革和突破，广大优秀的数学教师都开始探索新的数学教学策略，并努力创新教法，提高课堂教学的效率。作为新课程背景下的初中数学教师，唯有适应新课程改革的要求，积极参与教学实践，不断丰富教学经验，才能逐步优化初中数学的课堂教学方法，进而促进初中数学课堂教学的有效开展。

【关键词】新课程背景 初中数学 优化教学的策略 教师

【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089（2017）25-0136-02

新课程改革的深入推进使素质教育成为广大教师追求的教育目标，素质教育是教育工作者以提升受教育者诸方面能力为教学目标的一种新型教育模式，它既重视学生学习能力的培养，又注重学生的身心健康和个人素质的综合发展。与传统应试教育相比，素质教育以学生为本，更具人性化的教育特点，并且符合当代教育发展要求。初中数学是初中教育教学工作的重要组成部分，通过学习数学，学生能够掌握基本的数学学科知识，并且在学习数学的过程中逐步培养数学应用能力，使学生逐渐形成数学思维，能够科学地去思考和解决一些学习或者日常生活中的问题。数学教师要不断进行教学创新，寻找优化数学学科教学的有效途径，使数学教学符合学生的身心发展特点和学科能力要求。笔者通过自己在日常教学实践中的一些经验，结合个人对新课程理念的理解，在此就优化初中数学教学方法简单谈谈自己的看法。

一、注重课堂问题导入，培养学生的问题意识

课堂导入是教师在讲授课程内容时创设教学情境，引出教学目标的重要途径。良好的课堂问题导入能够有效吸引学生的课堂注意力，因此，初中数学教师应当重视课堂问题导入，并根据初中生的身心发展特点和兴趣所在，创设合理的问题情境，充分调动学生的数学思维，使学生积极主动的进行课堂学习，并且保持良好的学习状态。

案例一 《勾股定理》教学时设置这样问题情景：

（1）将一个边长为3cm的正方形纸片，沿着对角线折叠，你能知道折痕的长度吗？

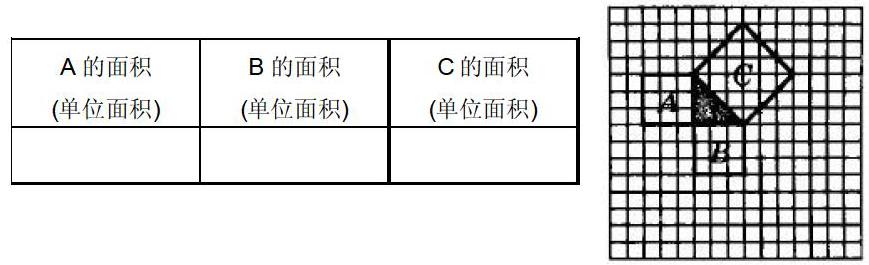
（2）若把折叠成的直角三角形放入图中的格点，（每个小正方形的边长都是1cm），你能算出斜边的长度吗？

（3）观察图形并完成表格

①图中，A、B、C之间有什么关系？

②从图中你能发现什么？

通过折纸问题，学生们从简单操作中的数量关系产生“疑”的问题情境，情境中的问题更加贴近学生探索勾股定理的“最近发生区”，从而转化成研究问题的本质和对象，使折纸转化为探索直角三角形三边关系的载体，为本节课教学目标的达成创造了有利条件。

学生带着问题进入课堂学习，不仅能够有步骤的建立解决问题的思路，寻求到问题解决的办法，还能使学生在解决问题的过程中逐步提高学习能力，并产生问题意识。当学生在数学学习中面临各种问题时，就会产生解决问题的想法，并独立分析问题，进行步骤推理，进而确定问题解决的方向。初中生的思想比较活跃，有着极强的好奇心和探索欲，这也正是培养学生学习能力的黄金时期，教师应当转变传统教育观念，为学生营造一个轻松的学习氛围，使同学们敢于设问，善于发问，不断提高学生的学习积极性。

二、鼓励探究性学习，提高学生的自主学习能力

传统的初中数学教学以教师为主导，教师是教学目标的制定者和教学计划的执行者，学生处于被动接受的位置，传统的教学方式在很大程度上遏杀了学生的学习积极性，学生会逐渐依赖教师的“教”，而忽视自己的“学”。数学学习是一个不断进行知识建构的过程，学生是学习的主体，只有学生愿意进行主动的学习探索，才能使学习兴趣得到培养，进而提高数学学习能力。探究学习是指学生独立发现问题并自主探究问题，同时在这个过程中获得自我能力发展的一种学习方式。探究学习是一个情感活动的过程，学生在独立学习时，会运用自己已经掌握的数学知识和现阶段的数学能力，去寻找解决问题的方法，当学生在探究过程中遇到阻碍时，会产生解决问题的想法，并积极投身于学习实践中。当问题得到解决后，学生会获得一种学习成就感，并且相信自己的学习能力，从而在今后的数学学习中树立学习自信心，激发学习探究的动力。探究性学习能够将教师的“教”向学生的“学”转变，原本处于被动接受的学习者变为积极主动的探究者，这样的教学转变是素质教育的基本要求，也是新课程改革得以落实的重要途径。

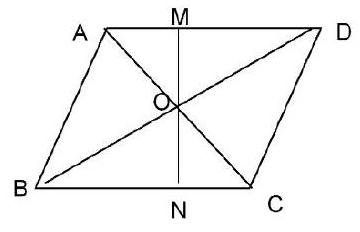
案例二 在上平行四边形及其性质3时，我在讲课过程中只是拿了一个平行四边形的自制教具，让学生自己得出了平行四边形的对角线互相平分的结论。怎样证明这个问题，我让学生自己解决。教材中只给出了证△OAB≌△OCD的一种解法，大多数学生很快解决了问题。但有一个学生提出了作OM⊥AD，ON⊥BC，因为是一个与众不同的想法，所以我让同学们一起讨论此法是否可行？马上有同学提出异议，说不行。其实不能证明是很显然的事，但节外生枝的是下面有同学随口说出了“只有三个角等，不能证全等”。又出现了新的错误，∠AOM和∠CON到底等不等？他们是对顶角吗？这无意中引出了一个新的问题，怎样证M、O、N 三点共线？ 这些突发的问题，课前不可能有准备。但课堂不应局限于预先设定的模式，于是我就放手让学生自主探究。我们的学生真是高明的，片刻沉默后，就有学生举手，思路如下：

△OAM和△OCN的三角形内角和都是180°，

∵AD∥BC， ∠MAO=∠NCO，

又∵OM⊥AD，ON⊥BC，

∴ ∠AMO=∠CNO=90°

∴∠AOM= ∠CON，

∵∠AOM+∠COM=180°，

∴∠CON+∠COM=180°，

∴M、O、N三点共线。

另一位同学提出了更简单的思路：延长NO交AD于M1，

∵AD∥BC， ∴∠DM1N+∠CNM1=180°，

∵又ON⊥BC，∴∠CNM1=90°，∴∠DM1N=90°

∴OM1⊥AD，因为过一点有且只有一条直线与AD垂直，所以点M与点M1重合，

∴M、O、N三点共线。

当时的唯一感觉是：我们的学生真是伟大呀！数学家华罗庚曾经说过“教师之为教，不在全盘授予，而在相机诱导。必令学生运其才智，勤其练习，领悟之源广开，纯熟之功弥深，乃为善教者也。”这句话深刻的指出了自主学习在数学学习中的重要意义。

三、重视教学评价过程，形成发展性的评价模式

教师在制定教学评价标准时要注重评价内容的全面性和客观性，要多用形成性评价而不是总结性评价，比如“尽管你的回答不够全面，但是，老师仍然欣赏你的机智和勇敢。”……作为新课程背景下的初中数学教师，我们要以了解学生的学习过程和阶段性学习进展为主要评价目标。不同学生的数学学习基础和数学学习能力各不相同，教師在制定评价标准时必须考虑到学生间的差异性，依据不同学生之间的学习差异来制定科学的、合理的评价标准和评价内容。良好的教学评价具有导向性，能够使教师及时了解学生的学习情况，并且根据学生的学习情况改变教学策略，制定新的与学生发展相适应的教学目标。激励性的评语能够激发学生的学习热情，增强学生的学习信心，从而不断获得个人能力的发展和学习的进步。教学评价不仅有助于学生个人能力的发展，还能够有效促进教师的专业成长。在课程改革不断发展的现阶段，我们要顺应新课程对教学评价的具体要求，确立正确的评价方向，制定科学的评价内容，使教学评价标准符合时代发展的要求，并且能够促进初中数学教学工作的发展与进步。

人们的日常生活和生产劳动都离不开数学知识。从学生学习的角度来讲，学习数学能够使自己养成严谨的学科态度，具备严密的数学思维和逻辑思维能力，同时，学生们还可以利用已掌握的数学学科知识来解决生活中的问题。因此，我们要重视初中数学教学工作，不断寻找科学的教学策略，努力优化教学方式，为初中数学教学工作注入源源不断的活力。

参考文献：

[1]岑燕斌，王珏琴，王荣方，刘文武.民族地区中学“问题探究与自主创新”数学教学模式的探索与实践研究报告[J].黔南民族师范学院学报.2005（03）.

[2]刘岗.数学学习评价的现状与思考——山西省临汾地区初级中学数学学习评价改革的调查报告[J].当代教育论坛（管理研究）.2010（05）.

[3]陈彩云.以适应与转化原理为指导优化教学过程——从系统科学的角度谈提高教学质量的策略[J].山东教育科研.1996（06）.