弹性边界条件下的功能梯度圆柱壳振动特性研究

陈金晓，梁 斌

（河南科技大学 土木工程学院，河南 洛阳 471023）

弹性边界条件下的功能梯度圆柱壳振动特性研究

陈金晓，梁 斌

（河南科技大学 土木工程学院，河南 洛阳 471023）

文章研究了功能梯度材料圆柱壳在弹性边界条件下的振动特性。在Flügge理论的基础上，基于波动法，采用改进傅里叶级数的计算方法建立FGM圆柱壳的振动特征方程，并推导出了弹性边界条件下FGM圆柱壳的固有频率参数表达式。通过与两端简支条件下的FGM圆柱壳的计算结果进行对比，验证了文中计算方法的正确性和有效性。通过算例，研究了在约束刚度不断变化过程中，FGM圆柱壳的固有频率在不同模态下的变化规律;分析了在弹性边界条件下，壳体尺寸、体积分数等因素对FGM圆柱壳固有频率的影响。

弹性边界；功能梯度材料；圆柱壳；波动法；固有频率

0 引 言

圆柱壳结构是一种在航空航天、海洋工程等领域广泛应用的结构形式。考虑功能梯度材料的圆柱壳结构，由于功能梯度材料和圆柱壳的结合，把材料的性能和圆柱壳的优异特性更好的体现出来，功能梯度材料圆柱壳结构也具有了更好的应用价值。因此，研究功能梯度材料圆柱壳在不同情况下的动力学行为特性，对这类结构在实际工程中的安全应用具有非常重要的意义。

目前，关于功能梯度材料圆柱壳在不同边界条件下的动力性能研究已经取得一些成果。Loy等[1-2]基于经典薄壳理论，利用Rayleigh-Ritz法推导出FGM圆柱壳自由振动的特征方程，研究了在不同边界条件、体积分数、材料组分等因素下，固有频率的变化规律曲线。Li等[3-4]在波动法的基础上，研究了圆柱壳在不同边界条件下的自由振动特性，并将波动法与其它方法进行对比，发现了波动法在计算上的优越性。Zhu等[5]基于Flügge理论，运用波动法研究了水下圆柱壳的耦合振动特性。Loy等[6]根据Love一阶近似理论，研究了两端简支、两端固支、两端自由等边界条件下多层圆柱壳的固有频率变化规律，同时给出了几种边界条件下固有频率的振型。李等[7-8]在Love薄壳理论的基础上，根据改进的傅里叶级数方法，并结合Rayleigh-Ritz法，研究了弹性边界条件下旋转功能梯度材料圆柱壳的自由振动特性，分析了边界约束刚度、材料组分、壳体尺寸等因素对固有频率的影响。马旭等[9]基于波动法，采用改进傅里叶级数方法建立弹性约束边界条件下圆柱壳的振动模型，研究了圆柱壳在弹性约束边界条件下的自由振动和强迫振动特性。刘伦等[10]基于Gram-Schmidt正交化建立圆柱壳的振动位移表达式，根据Sanders壳体理论和Rayleigh-Ritz法，在验证了此方法的正确性的基础上，研究了边界各个方向的约束刚度对正交加肋圆柱壳固有频率的影响。以及其他研究文献[11-12]。但是由于弹性边界的复杂性，尚未发现考虑弹性边界条件下，功能梯度材料圆柱壳振动特性的研究文献。

本文在Flügge理论的基础上，采用波动法和改进傅里叶级数方法建立弹性边界条件下FGM圆柱壳振动频率的特征方程，运用计算软件MATLAB求解特征方程得到圆柱壳在弹性边界下的固有频率。通过退化计算，将两端简支的FGM圆柱壳的固有频率的计算结果进行对比，验证了本文计算的有效性和正确性。最后通过算例，探讨了不同模态下约束刚度对FGM圆柱壳自由振动的影响，同时研究了在弹性边界条件下，材料体积分数、壳体尺寸等因素对圆柱壳自由振动的影响。

1 力学模型

图1所示为圆柱壳的力学模型，R表示平均半径，L表示圆柱壳长度，h表示圆柱壳壁厚，本文在圆柱壳的中面上建立正交坐标系 x，θ，（ ）z，其中x，θ和z分别为圆柱壳的轴向、环向和径向坐标。

图2中所示为弹性边界约束模型，k0，k1为径向约束刚度，K0，K1为扭转约束刚度。通过不同的刚度值组合可以实现所有的边界条件。例如，当刚度值均为0时,代表自由边界条件；当扭转刚度值为0，径向刚度值为无穷大时，代表两端简支边界条件；当刚度值均为无穷大时，代表两端固支边界条件。

假设圆柱壳沿厚度方向的弹性模量与材料组分的百分比有关，则其函数表达式为：

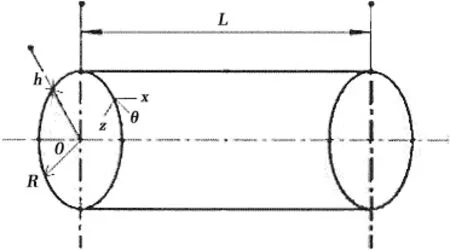
图1 环肋圆柱壳及其环肋截面模型Fig.1 Geometry of ring-stiffened cylindrical shell and stiffener

其中：V1和V2分别是圆柱壳内、外表面材料的体积百分比，P为幂率指数，其取值范围为0≤P≤∞。

当圆柱壳的组分材料为两种时，假定内、外表面材料参数分别为弹性模量E1，E2、质量密度ρ1，ρ2、和泊松比υ1，υ2，环肋FGM圆柱壳的等效弹性模量E，泊松比υ，材料密度ρ表示如下：

图2 弹性边界Fig.2 Elastic boundary supports

2 理论推导

根据Flügge理论[11]，圆柱壳的运动方程为：

用波动法表示的圆柱壳振动位移方程如下：

其中：Um，Vm，Wm分别表示x，θ，z方向的波幅，ω表示固有角频率，km的大小与约束边界的约束刚度有关，文献[12]中采用改进傅里叶级数的计算方法求km。

波动法的基本思想是：在圆柱壳的弯曲振动分析中，相应边界条件下的圆柱壳的轴向波数km可以用梁的弯曲振动波数来替代。梁的运动微分方程为：

式中：DL，ρL，AL代表梁的刚度，密度和横截面面积。

p（）x是为了克服余弦级数的不连续性而引入的辅助函数。

将（7）式代入（6）式得到：

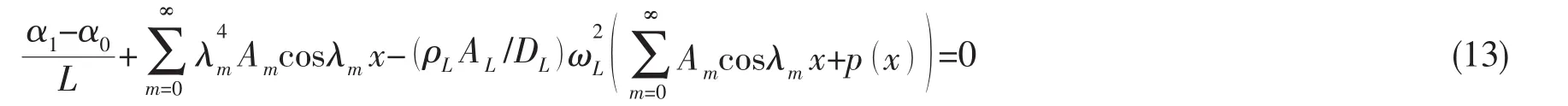
将（13）式进行推导，最终可以化为标准的矩阵求解特征值问题，求解方程可以得到相应的轴向波数。将相应的轴向波数代入（5）式，并将（5）式代入（4）式可以得到用矩阵表示的运动方程，求解运动方程，进而得到圆柱壳的固有频率。

3 数值计算及分析

3.1 正确性和有效性分析

为了验证本文研究方法的正确性和有效性，表1给出了两端简支条件下功能梯度材料圆柱壳固有频率的计算结果，并与已有文献的计算结果进行了对比分析，本文的计算结果与文献[1]中的计算结果存在着误差，但均控制在百分之零点几之内，这个误差在工程允许的误差范围之内。结果分析验证了本文求解弹性边界下FGM圆柱壳固有频率的计算方法的正确性和有效性。表1中计算参数均与文献[1]中的相同。n表示周向波数。

表1 两端简支条件下功能梯度材料圆柱壳固有频率计算结果对比分析Tab.1 Comparison between the results of calculation of the natural frequencies for FGM cylindrical with SS-SS

3.2 边界刚度对FGM圆柱壳的振动特性的影响

本文通过多组算例研究了弹性边界条件下FGM圆柱壳的振动特性，在不同边界约束的情况下，通过改变约束刚度、壳体尺寸、体积分数等因素，分析了圆柱壳固有频率的变化规律，计算结果见图3-12。本文算例中，规定圆柱壳的功能梯度材料组分为外表面不锈钢、内表面氮化硅，不锈钢和氮化硅的材料参数分别为：E2=2.077 88×1011，υ2=0.317 756，ρ2=8 166；E1=3.222 7×1011，υ1=0.24，ρ1=2 376。文中计算时所选用的参数为：h=0.002，R=1，L=20，m=1，P=1。

为了便于分析，计算过程中均采用无量纲约束刚度（约束刚度值除以弯曲刚度DL），即：k0′=k0/DL，k1′=k1/DL，K0′=K0/DL，K1′=K1/DL。计算中选用两种边界约束情况，一种为k0′，k1′为无穷大、K0′，K1′同时从1增大至100 000，即边界条件从两端简支到两端固支中变化，视为边界约束A；另一种为k0′，K0′为无穷大、K1′=1、k1′从1增大至100 000，即边界条件从一端固定、一端自由到一端固定、一端简支中变化，视为边界约束B。计算过程中无穷大均取1010。图3中，约束刚度值均取对数值log k0′，log k1′，log K0′，log K1′表示，其余情况下的约束刚度值均用实际值表示。

3.2.1 约束刚度对FGM圆柱壳固有频率的影响

图3和图4给出了两种边界约束情况下，FGM圆柱壳固有频率在不同n值情况下随着约束刚度增大的变化规律曲线。可以看出，随着n值的增大，约束刚度对固有频率的影响在减弱，当n＞3时，约束刚度对固有频率的影响并不明显，基本上可以忽略不计。当n值较小时，两种边界约束下的固有频率均随着约束刚度的增大先增大后逐渐趋于一个定值。两种边界约束情况下，当约束刚度在1～1 000时，随着约束刚度的增大，固有频率亦增大，但是在约束刚度在100～1 000时，增大幅度大幅度减小，当约束刚度大于1 000之后，随着约束刚度的增大，固有频率的大小已趋于稳定。对比图3和图4，在固有频率增大过程中，边界约束B时，固有频率（n=1）的增大幅度更大。在约束刚度一定时，固有频率随着n值的增大先减小后增大。

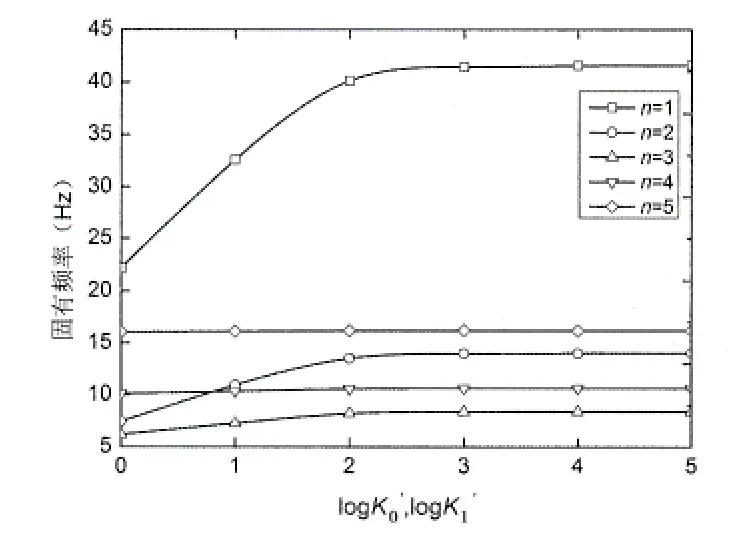
图3 不同n值下固有频率变化规律曲线（边界约束A）Fig.3 Variation of natural frequency with different circumferential wave number (boundary constraints A)

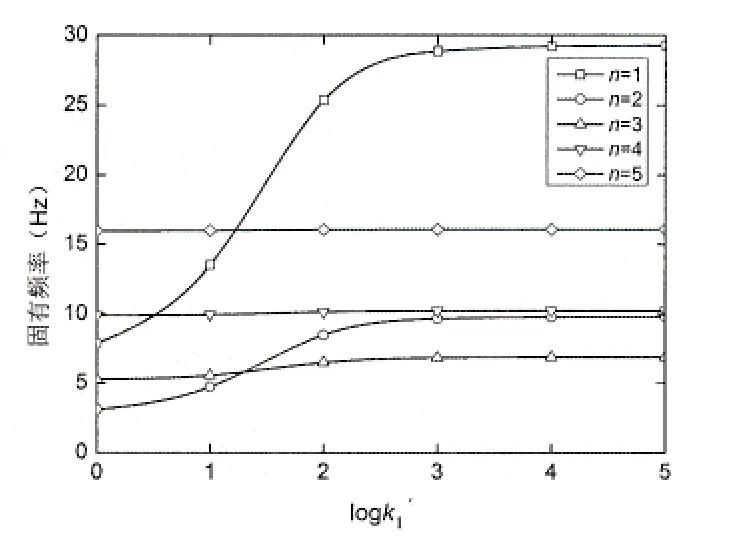
图4 不同n值下的固有频率变化规律曲线（边界约束B）Fig.4 Variation of natural frequency with different circumferential wave number (boundary constraints B)

图5 不同模态下的固有频率变化规律曲线（边界约束A）Fig.5 Variation of natural frequency with different modal shapes(boundary constraints A)

图6 不同模态下的固有频率变化规律曲线（边界约束B）Fig.6 Variation of natural frequency with different modal shapes(boundary constraints B)

图5和图6给出了两种边界约束情况下，FGM圆柱壳固有频率在不同模态下随着约束刚度的增大的变化规律曲线。从图中可以看出，固有频率随着轴向半波数m值的增大而增大，且增大幅度比较明显。边界约束A时，随着约束刚度的增大，三种模态下固有频率的变化规律大致相同；边界约束B时，随着约束刚度的增大，三种模态下固有频率的变化规律出现了不同，在模态（1，2）时，固有频率的增大主要出现在k1=1～100时；在模态（2，3）时，固有频率的增大主要出现在k1=10～1 000时：在模态（3，5）时，固有频率的增大主要出现在k1=10～10 000时，且是一个缓慢上升的过程，上升幅度比较小。由此可见，在约束刚度增大的过程中，n值对固有频率的变化规律的影响比m值的大。

3.2.2 FGM圆柱壳在弹性边界下的自由振动

基于上述结论，以下计算中均取：K0′=10，K1′=10（边界约束A）；k1′=10（边界约束B）。图7和图8给出了两种边界约束情况下，FGM圆柱壳的固有频率在不同n值时，随L的增大的变化规律曲线。从图中可以看出，两种边界约束情况下，随着L的增大，固有频率的变化规律大致相同：均随着L的增大而不断减小，且减小幅度也在不断地下降；当L从2增大到5时，固有频率的下降幅度最大；不同的边界约束条件只是改变了固有频率的大小。固有频率均随着n值的增大先减小后增大（边界约束B情况下L=2除外），但固有频率最小时的n值不同；边界约束B情况下L=2时，固有频率随着n值的增大而不断减小。

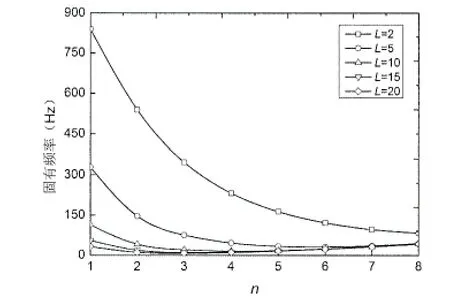
图7 不同L下的固有频率变化规律曲线（边界约束A）Fig.7 Variation of natural frequency with different length of the shell(boundary constraints A)

图8不同L下的固有频率变化规律曲线（边界约束B）Fig.8 Variation of natural frequency with different length of the shell(boundary constraints B)

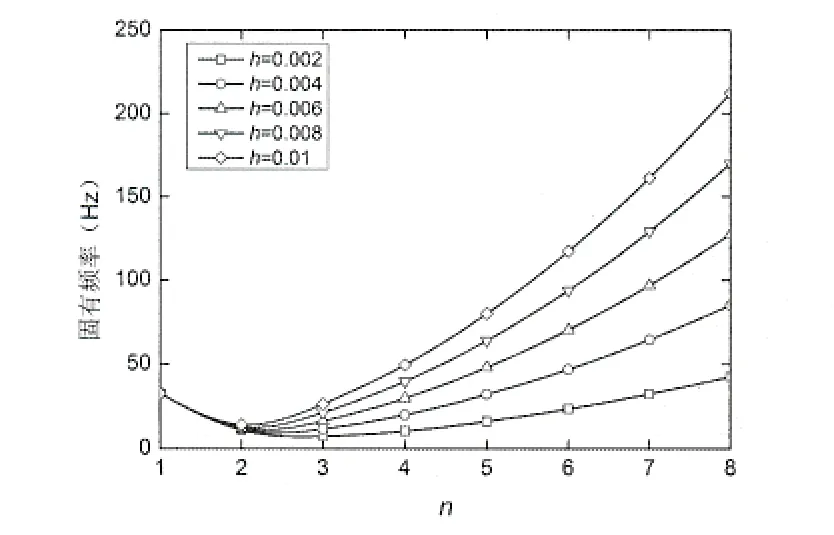
图9 不同h下的固有频率变化规律曲线（边界约束A）Fig.9 Variation of natural frequency with different thickness of the shell(boundary constraints A)

图10不同h下的固有频率变化规律曲线（边界约束B）Fig.10 Variation of natural frequency with different thickness of the shell(boundary constraints B)

图9 和图10给出了两种边界约束情况下，FGM圆柱壳的固有频率在不同n值时，随h的增大的变化规律曲线。从图中可以看出，固有频率均随着h值的增大而增大，但当n=1时这种现象并不明显。固有频率均随着n值的增大先减小后增大，且固有频率的最小值均出现在n=2时。对比图9和图10，在n=1～3时，边界约束A的固有频率明显大于边界约束B的固有频率，当n＞3时，边界约束的改变对固有频率的影响基本上可以忽略不计。

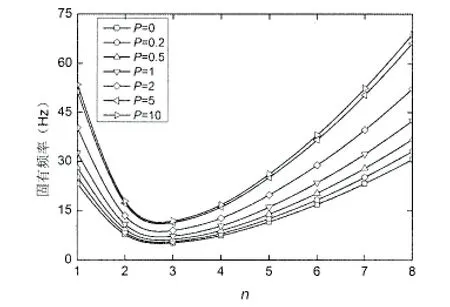
图11 不同P下的固有频率变化规律曲线（边界约束A）Fig.11 Variation of natural frequency with different volume fraction(boundary constraints A)

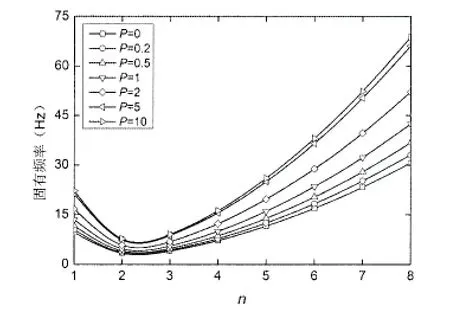
图12不同P下的固有频率变化规律曲线（边界约束B）Fig.12 Variation of natural frequency with different volume fraction(boundary constraints B)

图11 和图12给出了两种边界约束情况下，FGM圆柱壳的固有频率在不同n值时，随P的增大的变化规律曲线。从图中可以看出，两种边界约束有着相似的变化规律，固有频率均随着P值的增大而增大；固有频率均随着n值的增大先减小后增大，但固有频率最小时的n值不同，边界约束A时，n= 3时，固有频率最小，边界约束B时，n=2时，固有频率最小。对比图11和图12，边界约束对固有频率的影响只是在n=1～3时比较明显，此时边界约束A的固有频率明显大于边界约束B的固有频率，但当n＞3时，这种现象弱化了许多。

4 结 论

（1）固有频率随着约束刚度的增大先增大，之后趋于一个定值，且随着n的增大，约束刚度对固有频率的影响可以忽略不计。边界约束情况不同，随着约束刚度的变化，固有频率的变化速率差距很大。

（2）在约束刚度一定的情况下，固有频率随着m值的增大而增大，随着n值的增大，固有频率先减小后增大。不同模态（m，n）下，随着约束刚度的增大，固有频率的反应灵敏度不同。

（3）在n值较小时，固有频率均随着L的增大而显著减小；固有频率随着h的增大而增大；固有频率随着P值的增大而增大。

（4）边界约束条件对固有频率的影响只在n值较小的情况下比较明显，而这种影响只是改变了固有频率的大小，对固有频率的变化规律并无太大影响。

[1]Loy C T,Lam K Y,Reddy J N.Vibration of functionally graded cylindrical shells[J].International Journal of Mechanical Sciences,1999,41(3)：309-324.

[2]梁 斌,李 戎,张 伟,等.功能梯度材料圆柱壳的振动特性研究[J].船舶力学,2011,15(1-2)：109-117.Liang B,Li R,Zhang W,et al.Vibration characteristics of functionally graded materials cylindrical shells[J].Journal of Ship Mechanics,2011,15(1-2)：109-117.

[3]Li X B.Study on free vibration analysis of circular cylindrical shells using wave propagation[J].Journal of Sound and Vibration,2008,311(3-5)：667-682.

[4]Zhang X M,Liu G R,Lam K Y.Vibration analysis of thin cylindrical shells using wave propagation approach[J].Journal of Sound and Vibration,2001,239(3)：397-403.

[5]Zhu X,Ye W B,Li T Y,Chen C.The elastic critical pressure prediction of submerged cylindrical shell using wave propagation method[J].Ocean Engineering,2013,58(1)：22-26.

[6]Loy C T,Lam K Y.Effects of boundary conditions on frequencies of a multi-layered cylindrical shell[J].Journal of Sound and Vibration,1995,188(3)：363-384.

[7]李文达,杜敬涛,杨铁军,等.弹性边界约束旋转功能梯度圆柱壳结构自由振动行波特性分析[J].应用数学和力学,2015,36(7)：710-723.Li W D,Du J T,Yang T J,et al.Traveling wave mode characteristics of rotating functional gradient material cylindrical shell structures with elastic boundary constraints[J].Applied Mathematics and Mechanics,2015,36(7)：710-723.

[8]李文达,杜敬涛,杨铁军,等.基于改进傅里叶级数方法的旋转功能梯度圆柱壳振动特性分析[J].哈尔滨工程大学学报,2016,37(3)：388-393.Li W D,Du J T,Yang T J,et al.Vibration characteristics analysis of the rotating functionally graded cylindrical shell structure using an improved Fourier series method[J].Journal of Harbin Engineering University,2016,37(3)：388-393.

[9]马 旭,杜敬涛,杨铁军,等.基于波传播方法的边界条件对圆柱壳振动特性的影响分析[J].振动工程学报,2009,22 (6)：608-613.Ma X,Du J T,Yang T J,et al.Analysis of influence of boundary conditions on cylindrical shell dynamics based on wave propagation approach[J].Journal of Vibration Engineering,2009,22(6)：608-613.

[10]刘 伦,曹登庆,孙述鹏,等.弹性边界约束的正交加肋圆柱壳振动特性分析[J].船舶力学,2016,20(8)：1016-1027.Liu L,Cao D Q,Sun S P,et al.Vibration analysis of orthogonal stiffened cylindrical shells constrained by elastic boundary[J].Jounalof Ship Mechanics,2016,20(8)：1016-1027.

[11]Flügge W.Stresses in shells[M].Springer,New York,1973.

[12]Li W L.Free vibration of beams with generalboundary conditions[J].Journal of Sound and Vibration,2000,237(4)：709-725.

Study on the vibration of functionally graded material cylindrical shells under elastic boundary conditions

CHEN Jin-xiao,LIANG Bin
(Civil Engineering School,Henan University of Science and Technology,Luoyang 471023,China)

The free vibration characteristics of functionally graded material(FGM)cylindrical shells under elastic boundary conditions is studied.Based on the Flügge theory,the vibration characteristic equations of FGM cylindricalshells is derived by wave method and Fourier series,and the frequency parameter expression of FGM cylindrical shells under elastic boundary conditions is obtained.The present analysis is validated by comparing results with FGM cylindrical shells with simply supported-simply supported(SS-SS).By numerical examples,the varying regularity of natural frequency change for FGM cylindrical shells under different mode with the elastic stiffness constantly changing is studied,and the effects of shell size,volume fraction on the natural frequencies of FGM cylindrical shell are illustrated.

elastic boundary;functionally graded material;cylindrical shell;wave method; natural frequency

TB535+.1

A

10.3969/j.issn.1007-7294.2017.07.010

1007-7294（2017）07-0880-08

2017-03-05

国家自然科学基金资助项目（51105132；11402077）；河南省自然科学基金项目（编号122300410112）

陈金晓（1991-），女，硕士研究生，E-mail：chenjinxiao0520@163.com；

梁 斌（1963-），男，教授，博士生导师，E-mail：liangbin4231@163.com。