过载保载对金属材料疲劳裂纹扩展速率影响研究

王 珂，王 哲，王 芳，崔维成

（1.江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003；2.上海海洋大学 深渊科学技术研究中心，上海 201306）

过载保载对金属材料疲劳裂纹扩展速率影响研究

王 珂1，王 哲1，王 芳2，崔维成2

（1.江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003；2.上海海洋大学 深渊科学技术研究中心，上海 201306）

文章基于载荷次序效应产生影响的原因和相关预报模型，提出了考虑单峰过载和保载共同作用下疲劳裂纹扩展速率预报模型。在文中提出的考虑载荷次序效应的疲劳裂纹扩展速率预报模型的基础上，对几种金属材料在单峰过载、多峰过载、过载与保载共同作用下疲劳裂纹扩展速率进行了预报研究，并将预报结果与相应试验结果进行了比较，对考虑载荷次序效应的疲劳裂纹扩展速率预报模型的适用性进行了验证。

载荷次序；裂纹扩展率；过载保载；潜水器

0 引 言

海洋环境具有较大的复杂性和多变性，海洋结构物在服役期间承受着周期性波动载荷的作用。因此，对潜水器耐压壳结构在变幅载荷作用下进行疲劳裂纹扩展速率和寿命预报具有更加实际的工程意义。研究结果表明，结构疲劳寿命的决定性因素为疲劳载荷幅值的大小和每个循环中的应力最大值，此外，载荷的加载频率、作用次序和载荷的正负等因素对结构的疲劳寿命也具有较大的影响。而大深度潜水器的耐压壳结构在服役期间承受着更加复杂的波动载荷，目前许多学者在对其寿命进行研究时，将耐压球壳结构的寿命问题视为结构的低周疲劳问题，而忽略载荷峰值处保载时间的影响。为了得到更加准确的结构疲劳设计，就要对室温下具有保载时间的变幅载荷结构疲劳性能进行研究。直到目前，还未有学者提出考虑保载时间和变幅载荷共同影响的疲劳寿命预报模型。

1962年，Schijve和Brock对2024-T3铝合金高载作用后的疲劳裂纹扩展速率进行了研究，发现在恒幅载荷作用下，每加一次高载，裂纹扩展速率就会立即降低，直到在低载下经历足够多循环后，裂纹扩展速率才能恢复到原来水平，即所谓过载迟滞效应[1]。之后，学者们开始研究在恒幅载荷中加入单个或多个超载和卸载的结构疲劳问题。McEvily等[2]、Tianwen等[3]、Kalnaus[4]和Makabe等[5]学者对不同材料的单峰过载和卸载进行了试验研究，试验研究结果表明，当恒幅载荷中间加入一次或多次过载时，会导致材料裂纹扩展速率降低、试件寿命增加，即发生迟滞效应；而在恒幅载荷中加入一次或几次卸载时，试件裂纹扩展速率增加，即产生加速效应。随后，Kalnaus[4]提出了单峰过载下疲劳裂纹扩展速率预报模型；Tianwen等[3]提出了一个修正Wheeler模型，用来预报材料的过载迟滞效应。

本文在考虑小裂纹的疲劳裂纹扩展速率预报模型[6]和考虑载荷次序效应的典型疲劳裂纹扩展速率预报模型基础上，提出了考虑过载和保载共同作用载荷次序效应下的疲劳裂纹扩展速率预报模型；并利用该模型对文献[4，7-8]中几种金属材料在单峰过载、多峰过载疲劳裂纹扩展速率进行了预报研究；此外对钛合金TC4ELI和X70[9]管线钢在峰值保载及过载和保载共同作用下疲劳裂纹扩展速率进行预报研究；并通过这几种金属材料疲劳裂纹扩展速率预报结果与相应试验值进行了对比研究，从而证明本文提出的考虑载荷次序效应的疲劳裂纹扩展速率模型的可靠性。

1 疲劳裂纹扩展速率预报模型

1.1 考虑载荷次序效应的疲劳裂纹扩展速率预报模型

近几十年，学者们对变幅载荷作用下疲劳裂纹扩展速率的预报进行了大量研究，并提出了一系列考虑载荷次序效应的疲劳裂纹扩展速率预报模型。1971年Wheeler[10]提出了考虑迟滞疲劳裂纹扩展行为的Wheeler模型。该模型认为：迟滞是由于高载在裂纹尖端引入了较大塑性区域而造成的。因此，Wheeler引入了一个载荷次序影响因子φR来体现载荷次序对疲劳裂纹扩展速率的影响：

式中：ai为低载时裂纹长度，m；ryi为低载作用下裂纹尖端塑性区域尺寸，m；aOL为过载时裂纹长度，m；rOL为过载作用时裂纹尖端产生的高载塑性区域；γ为形状指数。

Wheeler给出了低载作用和过载作用下的塑性区域尺寸分别为：

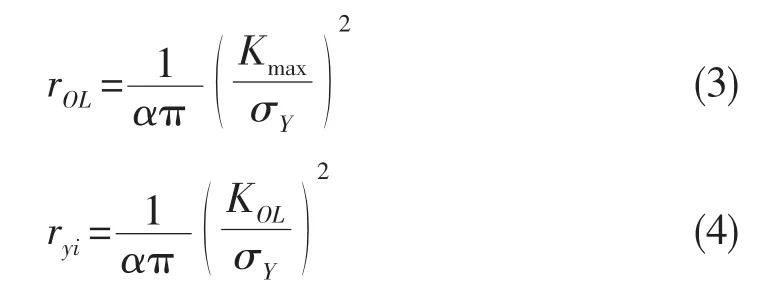
式中：α为塑性区域尺度系数，通过试验数据确定；σY为材料的屈服应力，MPa。

图1 Wheeler模型对裂纹扩展速率的预报结果与试验结果Fig.1 Prediction ofcrack growth rate after overloading using Wheeler’s model

由图1可以看出，虽然Wheeler模型能够较好地预报疲劳裂纹扩展速率的过载迟滞效应，但是对于预报延迟区域内裂纹扩展速率趋势存在一定的差异。为了更好地描述在过载延迟区域内疲劳裂纹扩展速率的变化情况，Zhao[3]和李珊珊[11]等人在Wheeler模型的基础上对载荷次序影响因子进行了修正，Zhao的修正模型如下式所示：

rpmr为联合考虑过载和裂纹扩展的有效剩余塑性区域大小，可表示为：

rpi为第i个载荷循环作用下的塑性区域的大小，表示为：

根据李珊珊的修正模型，过载单独作用时，载荷次序影响因子Φ表示为：

根据Rushton提出的rpOL过载引起的单调过载塑性区域尺寸可表示为：

rpR为裂纹长度为aR时裂纹尖端处塑性区大小，参照（7）式可表达为：

式中：△KR为裂纹长度为aR时的应力强度因子范围，为过载时裂纹长度，m；aR为裂纹扩展速率恢复到恒幅循环载荷作用下稳定水平时的裂纹长度，m，可表达为（11）式，可通过迭代求出aR。

1.2 保载和过载作用下疲劳裂纹扩展速率预报模型

对于图2中的载荷工况，即常幅循环载荷中存在一次过载和保载的载荷情况，在Chen等[12]过载预报模型的基础上，Wang[8]提出了预报该过载情况的裂纹扩展速率预报模型。该模型中假设单一拉伸过载和短时间的保载将不引起裂纹扩展，而是在裂纹尖端产生由于单峰过载和保载时间共同作用的单调塑性区域，图3描述了由于过载和保载裂纹尖端塑性区域分布。单峰过载和保载时间共同作用时修正因子Φ由（12）式表达，其中rOL和rdt分别为单峰过载和保载时间在裂纹尖端引起塑性区域的大小。

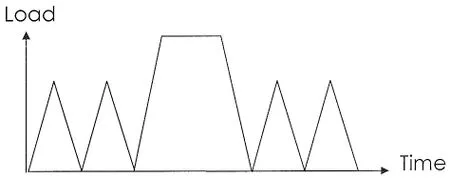
图2 具有过载和保载时间的循环载荷示意图Fig.2 Schematic representation ofthe load pattern for cyclic loading with overload and dwell time

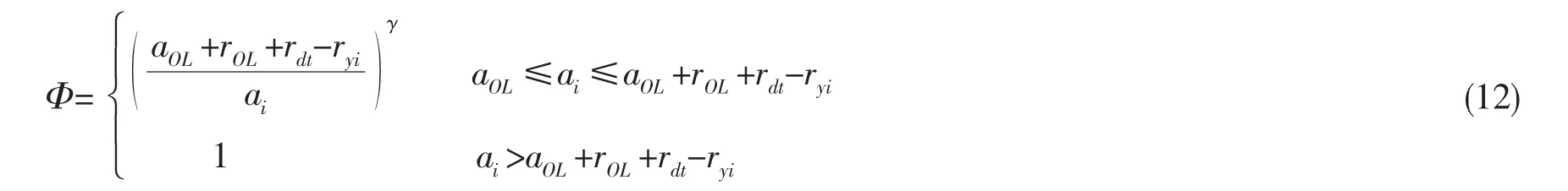
对于大多数材料，低温蠕变（＜0.25Tm）变形主要是由蠕变第一阶段决定的。在低蠕变应力和蠕变应变（＜2×10-3）时，许多材料第一阶段蠕变变形可以表示为对数形式，即ε=l ln t+C。对于具有较大第一阶段蠕变变形时，蠕变变形可以表达为指数形式，如（13）式所示。

式中：C1和k1为材料常数；T为时间，h。

根据Ramberg-Osgood的应力—应变曲线（14）式，将单调蠕变应力σcreep引起应变简单等效成一应力值 σep。

则由单峰过载和保载时间引起裂纹尖端应力强度因子KOLC可表达为：

单峰过载和保载时间引起裂纹尖端塑性区域尺寸rOLC可表达为：

因此，本文在Zhao[3]和Wang[8]模型的基础上，提出了预报具有单峰过载和保载共同作用下的载荷次序修正因子ΦRC模型。该模型假设：在短时间保载内裂纹不扩展；保载时间内裂纹尖端塑性区域尺寸增加速率与稳态蠕变速率相同。因此，将单峰过载和保载共同作用引起裂纹尖端塑性区域模型添加到有效剩余塑性区域中，具体表达如下式所示：

式中：rpOLC为联合考虑过载（单峰过载和保载时间）和裂纹扩展的有效剩余塑性区域大小，可表示为：

rpi为第i个载荷循环作用下的塑性区域的大小，表示为：

根据Wang[8]rOLC单峰过载和保载时间引起的单调过载塑性区域尺寸可表示为：

rpR为裂纹长度为aR时裂纹尖端处塑性区大小可表达为：

式中：△KOLC在过载和保载共同作用下裂纹尖端产生相同塑性区域时，对应单峰过载应力值下的应力强度因子为裂纹长度为aR时的应力强度因子范围，MPa m；aOLC为过载时裂纹长度，m；aR为裂纹扩展速率恢复到恒幅循环载荷作用下稳定水平时的裂纹长度，m，可表达为（23）式，可通过迭代求出aR。

2014年，Wang[6]提出了考虑小裂纹的疲劳裂纹扩展速率预报模型，如（24）式所示，该模型能够较好的预报金属材料疲劳小裂纹和长裂纹裂纹扩展行为，在该模型的基础上，将考虑了过载、保载时间的载荷次序影响因子表达式（18）代入该模型中。则考虑单峰过载、多峰过载、保载及过载与保载共同作用下疲劳裂纹扩展速率预报模型如（25）式所示：

过载作用或过载和保载时间共同作用时，

式中：Φ为载荷次序影响因子；ΦRC为考虑过载和保载时间的载荷次序影响因子；A为与疲劳循环载荷相关的材料和环境常数，MPa-mm1-m/2；a为裂纹长度，m；m表示疲劳循环载荷相关的裂纹扩展速率曲线斜率的常数；n为与循环项相关的不稳定扩展程度的表征指数；R为疲劳循环载荷应力比；Kmax表示最大应力强度因子为材料断裂韧性d为材料的内部裂纹长度，m；△Kth-s表示小裂纹扩展门槛值表示载荷比为R时，长裂纹扩展门槛值，表示交变载荷作用下的最大应力，MPa；k表示裂纹闭合水平随裂纹变化的参数，m-1。

2 载荷次序效应对裂纹扩展速率影响的预报研究

2.1 单峰过载对疲劳裂纹扩展速率影响的预报研究

Kalnaus[4]对SS304L不锈钢材料的载荷次序效应对疲劳裂纹扩展速率的影响进行了试验研究。对于过载主要进行了在相同基本疲劳循环载荷、不同单峰过载下疲劳裂纹扩展速率和不同基本疲劳循环载荷、相同单峰过载下疲劳裂纹扩展速率的研究。该材料的过载参数列于表1，对SS304L不锈钢材料单峰过载下疲劳裂纹扩展速率的预报结果如图4所示。

表1 SS304L 不锈钢单峰过载参数表Tab.1 Parameters of SS304L for fatigue crack growth under overload

续表1

图4 单峰过载作用下SS304L不锈钢裂纹扩展速率的预报结果与试验结果对比Fig.4 Comparison of prediction with test data of SS304L under single overload

由图4（a）、（b）、（c）和（d）的对比分析可以得到：在相同基本疲劳循环载荷△P时，裂纹扩展速率d a/d N最小值的试验结果与预报结果都随着单峰过载值POmax的增加而减小，即疲劳裂纹扩展速率过载迟滞效应变大，且过载影响区域随着过载增加变大。由图4（a）、（c）、（b）和（d）的对比分析可以得到：相同的单峰过载值POmax时，裂纹扩展速率d a/d N最小值的试验结果与预报结果都随着基本疲劳循环载荷△P的减小而减小，即疲劳裂纹扩展速率过载迟滞效应变大。预报模型（24）式对单峰过载疲劳裂纹扩展速率的预报结果与试验结果对比研究发现：单峰过载下疲劳裂纹扩展速率最小值的预报结果要低于试验结果；除此之外整个过载塑性区域内预报结果与试验结果吻合较好。因此，在相同的载荷比下，过载比OLR增大，过载迟滞效应变大。由上面研究可得，该预报模型对SS304L不锈钢的单峰过载迟滞现象具有较好的预报能力。

2.2 多峰过载对疲劳裂纹扩展速率影响的预报研究

基于考虑载荷次序效应疲劳裂纹扩展速率预报模型，对多峰过载作用下潜艇用高强钢HTS-A的疲劳裂纹扩展速率进行预报研究。Huang[7]对潜艇用高强钢HTS-A进行多峰过载疲劳裂纹扩展速率试验研究，试验中进行了四次过载比为OLR=2的过载作用，材料的过载参数列于表2中，图5为多峰过载作用下疲劳裂纹扩展速率预报结果与试验结果对比图。

表2 HTS-A多峰过载参数表Tab.2 Parameters of HTS-A for fatigue crack growth under multiple overload

由图5可以得到：对高强钢HTS-A进行四次过载作用时，均发生了疲劳裂纹扩展速率明显下降，即过载迟滞效应；该材料多峰过载迟滞效应的预报结果与试验结果吻合较好；随着过载作用时裂纹长度aOL的增加，过载迟滞效应影响区域也逐渐增加。因此，该考虑载荷次序的疲劳裂纹扩展速率预报模型能较好地反应该物理现象，并且预报结果与试验结果吻合较好。

2.3 过载和保载时间对疲劳裂纹扩展速率影响的预报研究

利用（18）式和（25）式对钛合金TC4ELI和管线钢X70在单峰过载和保载时间共同作用下疲劳裂纹扩展速率进行了预报研究。钛合金TC4ELI的过载参数列于表3中。在进行单峰过载和保载下疲劳裂纹扩展速率预报之前，要先对该两种材料进行了室温下的疲劳和蠕变试验研究，从而确定常幅载荷时过载保载共同作用下疲劳裂纹扩展速率预报模型中的模型参数，以及确定保载时间内裂纹尖端过载塑性区域增加的速度。

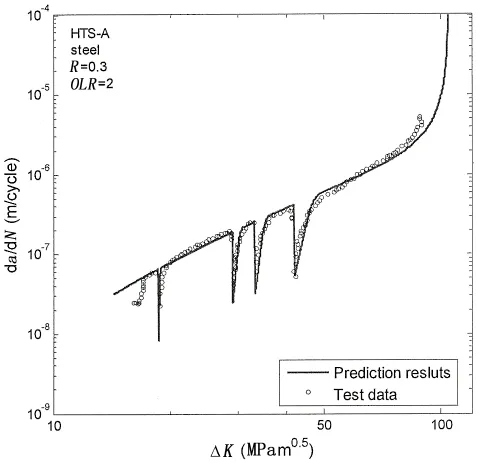
图5 多峰过载作用下HTS-A裂纹扩展速率的预报结果与试验结果对比Fig.5 Comparison of prediction with test data of HTS-A under multiple overload

表3 TC4 ELI过载参数表Tab.3 Parameters of TC4 ELI for fatigue crack growth under overload

图6为文献[7]中钛合金TC4ELI室温蠕变应变随时间变化的试验结果，通过对该曲线的拟合，得到该材料在蠕变载荷作用下应变变化速率为7.72E-6，从而可以确定保载时间内裂纹尖端塑性区域增加的速率。

图7为钛合金TC4ELI单峰过载疲劳裂纹扩展速率预报结果与试验值的对比图。根据图中试验曲线，在OLR=2情况下，TC4ELI材料的试验中出现了过载迟滞效应；当施加单峰过载时，疲劳裂纹扩展速率立即降低到最小值；由于该材料具有较高的屈服应力，所以单峰过载下裂纹尖端过载塑性区域尺寸小，即单峰过载疲劳裂纹扩展速率降到最小值之后，恢复到常幅载荷疲劳裂纹扩展速率的范围小。根据图中预报曲线，当施加单峰过载时，裂纹扩展速率预报结果立即降低到最小值，该最小值与试验结果吻合较好；单峰过载之后，疲劳裂纹扩展速率的预报结果在过载塑性区域内逐渐增加，当裂纹扩展到aR时，疲劳裂纹扩展速率的预报结果恢复到常幅载荷下疲劳裂纹扩展速率值。图中预报结果与试验值吻合较好。

图6 TC4 ELI蠕变应变随时间变化曲线Fig.6 Results of creep strain versus time curve for normal creep of TC4 ELI

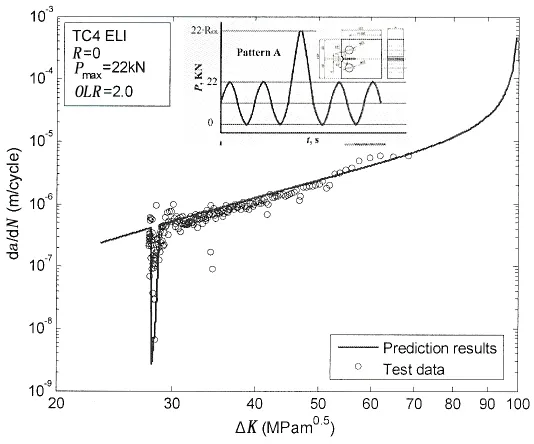
图7 单峰过载作用下TC4 ELI钛合金裂纹扩展速率的预报结果与试验结果对比Fig.7 Comparison of prediction with test data of TC4 ELI under single overload

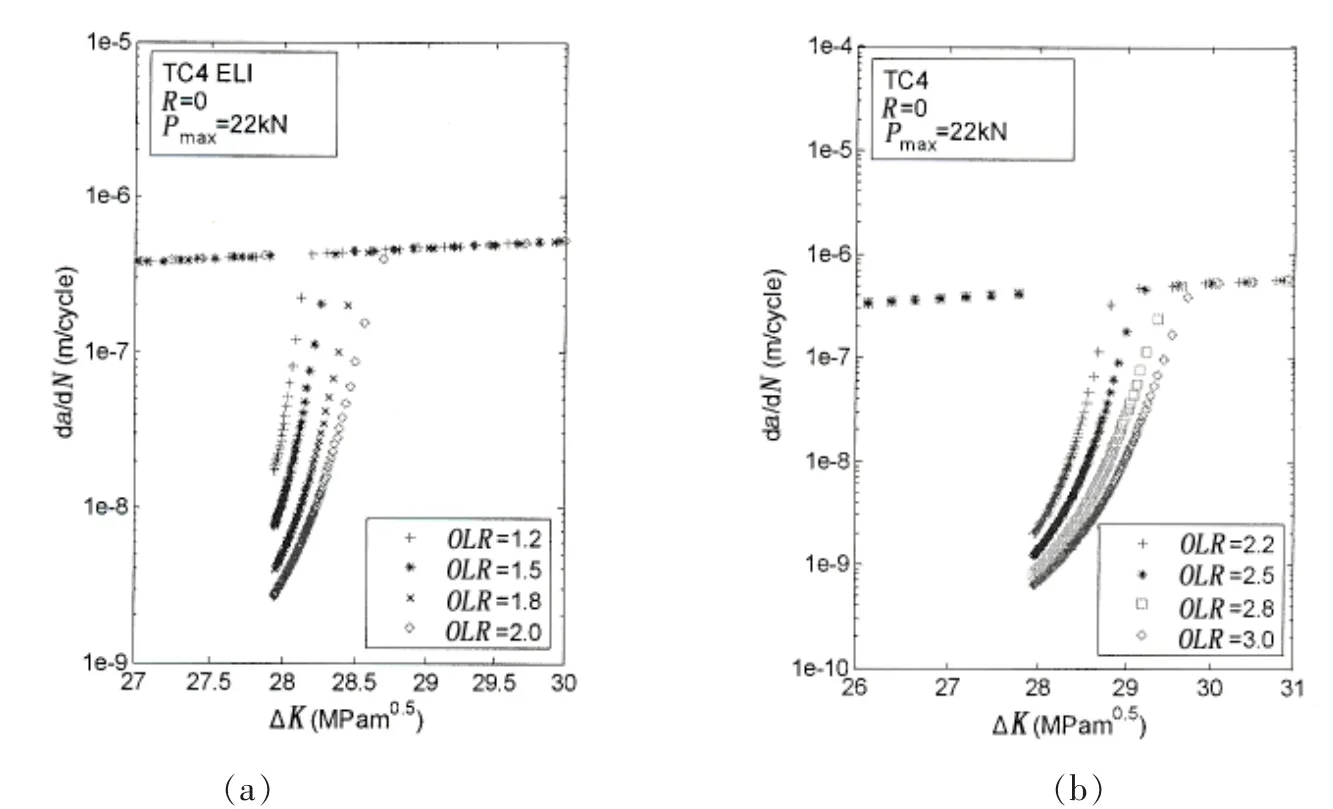
图8 过载比对TC4 ELI钛合金裂纹扩展速率影响的预报结果Fig.8 Prediction of overload effect to fatigue crack growth rate for TC4 ELI

图8为利用（18）式和（25）式对不同过载比下钛合金TC4ELI疲劳裂纹扩展速率的预报结果。由图可以得到，随着过载荷比OLR的增加，疲劳裂纹扩展速率降低至的最小值更低，裂纹尖端过载塑性区域尺寸增加，即疲劳裂纹扩展速率恢复区域变大，预报结果与试验结果一致。

图9为单一保载下钛合金TC4ELI疲劳裂纹扩展速率的试验结果与预报结果的对比图。单一保载试验中钛合金TC4ELI试件采用与单峰过载试验相同的标准CT试件，载荷比R=0，基本疲劳循环载荷△P为22 kN，在该基本循环载荷峰值处保载8h，即OLR=1.0。由图可以得到，虽然单一保载下疲劳裂纹扩展速率试验结果具有一定离散性，但总体上表现出了8h保载对疲劳裂纹扩展速率的迟滞效应；由于该材料具有较高的屈服应力，保载8h之后，裂纹尖端保载塑性区域小，即保载开始时的裂纹长度aOL到aR之间的距离小；图中曲线为考虑载荷次序效应疲劳裂纹扩展速率预报模型的预报结果，预报中各个过载参数采用与单峰过载时的参数相同，可以发现，保载8h疲劳裂纹扩展速率的预报结果与试验值吻合较好。

图10为利用（18）式和（25）式对不同保载时间下钛合金TC4ELI疲劳裂纹扩展速率的预报结果。由图可以得到，随着保载时间的增加，TC4ELI疲劳裂纹扩展速率减小到的最小值将更低，裂纹尖端过载塑性区域尺寸增加，即裂纹扩展速率恢复区域变大；通过钛合金TC4ELI室温蠕变、单峰过载和单一保载的试验结果和预报值的对比研究发现，室温情况下，钛合金TC4ELI对蠕变和单一保载并不是非常的敏感。

聂德福[8]对管线钢X70室温蠕变力学行为和室温蠕变对疲劳裂纹扩展影响进行了试验研究。试验研究表明X70管线钢对室温蠕变是比较敏感的，并且对该材料的不同热处理过程对其室温蠕变行为有着不同的影响；单峰过载和室温蠕变对X70管线钢的疲劳裂纹扩展速率产生了明显的过载迟滞效应。利用本文提出的考虑载荷次序疲劳裂纹扩展速率预报模型对X70管线钢的疲劳、单峰过载、单峰过载和保载载荷工况下的疲劳裂纹扩展速率进行预报研究，并将预报结果与聂德福试验结果进行对比研究，从而验证该模型的可靠性，管线钢X70的过载参数列于表4中。

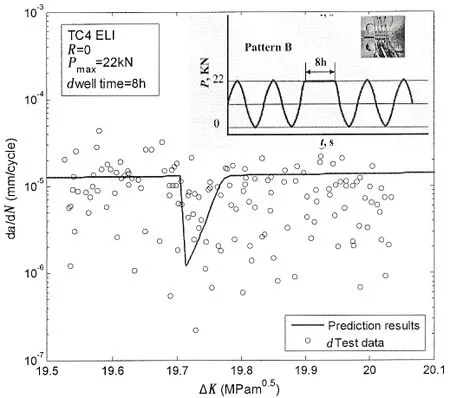
图9 8小时保载载作用下TC4 ELI钛合金裂纹扩展速率的预报结果与试验结果对比Fig.9 Comparison of prediction with test data of TC4 ELI under 8h dwell time

图10保载载作用下TC4 ELI钛合金裂纹扩展速率的预报结果Fig.10 Prediction of dwell time effect to fatigue crack growth rate for TC4 ELI

图11 为X70管线钢常幅载荷作用下疲劳裂纹扩展速率预报结果与试验值的对比图。图中疲劳裂纹扩展速率试验采用的是标准CT试件，载荷比R=0.05，试验材料X70管线钢的屈服应力为552MPa，拉伸极限值为649MPa，该材料的断裂韧性为110MPa。由图可以得到，在考虑小裂纹的疲劳裂纹扩展速率预报模型基础上，对常幅载荷作用下X70管线钢疲劳裂纹扩展的预报结果与试验值吻合较好；从而可以确定用于预报单峰过载和过载与保载共同作用两种载荷工况的模型参数。

表4 X70过载参数表Fig.4 Parameters of X70 for fatigue crack growth under overload

图12为X70管线钢不同过载比OLR下疲劳裂纹扩展速率预报结果与试验值的对比图。由图可以得到，不同单峰过载比下，当施加过载后X70管线钢疲劳裂纹扩展速率的试验值均立即下降到最小值，随后再逐渐恢复到常幅载荷作用下疲劳裂纹扩展速率的水平，即在三种OLR情况下X70均表现出明显的过载迟滞效应；随着过载比OLR的增加，单峰过载作用后的裂纹扩展速率下降到的最小值更低，裂纹尖端过载塑性区域增大，单峰过载迟滞效应影响区域增加；图中X70管线钢单峰过载疲劳裂纹扩展速率的预报结果与试验值吻合较好。总体上讲，（25）式能够较好地预报X70管线钢单峰过载下疲劳裂纹扩展试验中得到的各种物理现象。

单峰过载和保载共同作用时X70管线钢疲劳裂纹扩展速率预报结果与试验值的对比如图13所示。由图可以得到，单峰过载和保载时间共同作用时，在三种过载比下X70管线钢疲劳裂纹扩展速率立即下降到最小值，然后再逐渐恢复到常幅载荷疲劳裂纹扩展速率的水平，即产生了明显的过载迟滞效应；将图13与图12进行对比发现，在过载峰值处保载5 000s时，X70管线钢疲劳裂纹扩展速率的迟滞效应要大于单峰过载情况，这说明保载5 000s对疲劳裂纹扩展迟滞效应具有一定的影响；随着过载比OLR的增加，试验表现出疲劳裂纹扩展降低至的最小值更小和裂纹尖端的过载塑性区域均增加，这与单峰过载试验中的物理现象相一致；利用考虑载荷次序效应的裂纹扩展速率预报模型对在单峰过载和保载共同作用下X70疲劳裂纹扩展速率进行了预报，预报结果反映出了试验中疲劳裂纹扩展速率迟滞效应的现象。因此利用（18）式和（25）式能够较好地预报X70管线钢在单峰过载和保载共同作用下疲劳裂纹扩展速率的迟滞效应。

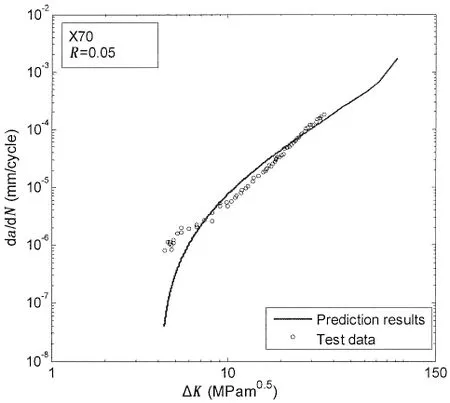
图11 常幅载荷作用下X70钢疲劳裂纹扩展速率的预报结果与试验结果对比Fig.11 Comparison of prediction with test data of X70 under constant amplitude load

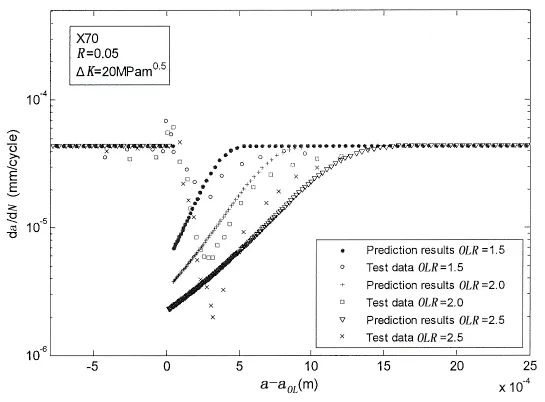
图12 单峰过载作用下X70钢疲劳裂纹扩展速率的预报结果与试验结果对比Fig.12 Comparison of prediction with test data of X70 under single overload

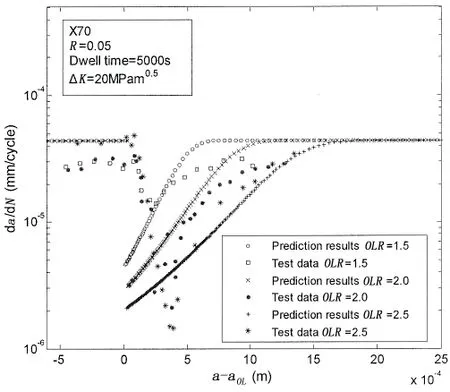
图13 单峰过载和保载时间共同作用下X70钢疲劳裂纹扩展速率的预报结果与试验结果对比Fig.13 Comparison ofprediction with test data of X70 under single overload and dwell time

3 结 语

本文在考虑小裂纹效应裂纹扩展速率预报模型的基础上，结合Wang和Zhao的载荷次序修正因子公式，提出了考虑载荷次序效应的疲劳裂纹扩展速率预报模型，并利用该模型对几种金属材料在单峰过载、多峰过载、保载和过载共同作用下疲劳裂纹扩展速率的迟滞效应进行了预报研究，并将预报结果与试验数据进行对比，从而验证了该模型的可靠性。主要得到以下结论：

（1）对SS304L和HTS-A材料在单峰过载和多峰过载下疲劳裂纹扩展速率进行了预报，发现相同基本疲劳循环载荷下，随着过载峰值的增加，过载后疲劳裂纹扩展速率降低的最小值更小，裂纹尖端过载塑性区域更大；当过载峰值相同时，随着基本疲劳循环载荷幅值的降低，过载迟滞效应更明显；单峰过载和多峰过载下预报结果与试验结果均吻合较好；

（2）对钛合金TC4单峰过载下和保载下疲劳裂纹扩展迟滞效应进行了预报研究，随着单峰过载比OLR增加，TC4过载迟滞效应更加明显；TC4单一保载8h的疲劳裂纹扩展速率预报结果与试验数据吻合较好，从而说明该模型可靠性；

（3）随着过载比OLR的增加，过载后X70钢的疲劳裂纹扩展速率降低至的最小值更低，裂纹尖端过载塑性区域尺寸更大，并且预报结果与试验数据吻合较好；不同过载比、过载和5 000s保载时间共同作用下X70钢裂纹扩展速率的迟滞效应较疲劳状态下产生更加明显的迟滞效应，随着过载比的增加迟滞效应增加，预报结果与试验值吻合较好。

因此，本文提出的考虑载荷次序效应的疲劳扩展速率预报模型对不同金属材料在单峰过载、多峰过载、过载与保载共同作用下裂纹扩展速率具有较强的预报能力，为真实研究海洋结构物在周期性波动载荷作用下的疲劳寿命预报研究提供了理论依据。

[1]陈传尧.疲劳与断裂[M].武汉：华中科技大学出版社,2002.

[2]McEvily A J,Ishihara S,Endo M.An analysis of multiple two-step fatigue loading[J].International Journal of Fatigue,2005,27(8)：862-866.

[3]Zhao T,Zhang J,Jiang Y.A study of fatigue crack growth of7075-T651aluminum alloy[J].International Journal of Fatigue,2008,30(7)：1169-1180.

[4]Kalnaus S,Fan F,Vasudevan A K,et al.An experimental investigation on fatigue crack growth of AL6XN stainless steel [J].Engineering Fracture Mechanics,2008,75(8)：2002-2019.

[5]Makabe C,Purnowidodo A,McEvily A J.Effects of surface deformation and crack closure on fatigue crack propagation after overloading and underloading[J].International Journal of Fatigue,2004,26(12)：1341-1348.

[6]Wang K,Wang F,Cui W C,et al.Prediction of shortfatigue crack growth of Ti-6Al-4V[J].Fatigue&Fracture of Engineering Materials&Structures,2014,37(10)：1075-1086.

[7]Huang X,Moan T.Improved modeling of the effect of R-ratio on crack growth rate[J].International Journal of Fatigue,2007,29(4)：591-602.

[8]Wang Fang,Cui Weicheng.Effect of plastic zone size induced by a single dwell overload on the fatigue crack growth rate under cyclic loading[J].Journalof Ship Mechanics,2014,18(9)：1117-1128.

[9]聂德福.结构钢的室温蠕变及其对疲劳裂纹扩展的影响[D].大连：大连理工大学,2008.

[10]Wheeler O E.Spectrum loading and crack growth[J].Journalof Fluids Engineering,1972,94(1)：181-186.

[11]李珊珊,崔维成.随机载荷次序效应对海洋结构物疲劳裂纹扩展的影响[J].船舶力学,2014,18(1-2)：139-151.Li Shanshan,Cui Weicheng.Random load sequence effect on fatigue crack propagation of marine structure[J].Journal of Ship Mechanics,2014,18(1-2)：139-151.

[12]Chen F L,Wang F,Cui W C.An improved constitutive model to predict fatigue crack growth rate under constant-amplitude loading with single and multiple overload[J].Proceedings of the Institution of Mechanical Engineers,Part M：Journal of Engineering for the Maritime Environment,2011,225(3)：271-281.

Effect of overload and dwell time on fatigue crack growth rate of metal materials

WANG Ke1,WANG Zhe1,WANG Fang2,CUI Wei-cheng2
(1.School of Naval Architecture and Ocean Eng.,Jiangsu University of Science and Technology,Zhenjiang 212003,China; 2.Hadal Science and Technology Research Center,Shanghai Ocean University,Shanghai 201306,China)

The prediction method for the fatigue crack growth rate considered single overload and dwell time is presented based on the cause of the effect of load interaction phenomenon and the relevant prediction models.The model is used to forecast fatigue crack growth rate of several metal materials under single overload,multiple overload and single overload and dwell-time,compared with the corresponding experimental data,to verify the reliability of the prediction method.

load interaction;crack growth rate;dwell overload;manned pressure hull

U663.9

A

10.3969/j.issn.1007-7294.2017.07.012

1007-7294（2017）07-0895-12

2017-01-18

王 珂（1976-），女，副教授，E-mail：ecsibelle@126.com；

王 哲（1991-），女，硕士研究生；

王 芳（1979-），女，副研究员。