基于弯扭耦合的破损船剩余强度评估方法研究

唐浩云，任慧龙，万 千，李陈峰，冯国庆

（哈尔滨工程大学 船舶工程学院，哈尔滨 150001）

基于弯扭耦合的破损船剩余强度评估方法研究

唐浩云，任慧龙，万 千，李陈峰，冯国庆

（哈尔滨工程大学 船舶工程学院，哈尔滨 150001）

破损舰船的剩余承载能力是检验结构设计合理性的一个重要指标。现有的破损舰船剩余承载能力评估主要考察垂向弯矩，缺乏考虑船体在斜浪状态下结构组合变形的综合影响。文章对破损舰船剩余承载能力评估方法进行了研究。在考虑船体组合变形的影响下，建立了弯扭耦合方程。通过非线性有限元计算，确定结构耦合系数，并在此基础上提出了破损舰船的剩余承载能力的可靠性评估方法。

极限弯矩；剩余强度；非线性有限元；可靠性

0 引 言

在营运过程中，由于意外事故常常造成船体结构的破损，威胁船舶的生命力和船员的生命安全。因此在设计阶段对破损船体的剩余强度进行准确评估，有利于正确有效地采取相应技术措施来实施救援和拖航。目前，国外各规范[1-3]己将剩余强度列入结构强度评估体系中，并提出了各自不同的评估方法，将剩余强度评估放在与原有强度评估同样重要的位置。

随着结构可靠性理论的迅速发展，其方法逐步应用于剩余强度的评估。Paik（1998）等[4]对一艘巴拿马型散货船进行了碰撞和搁浅损伤后的剩余强度计算，根据极限强度解析式，提出了基于剖面模数和极限强度的剩余强度安全系数。Guedes Soares（1996）等[5]对多种油船进行了可靠性分析，研究了垂向极限弯矩和水平极限弯矩共同作用下的极限状态方程。Wang（1996）[6]基于DNV规范提出了以屈曲衡准为指标的极限状态方程，并且考虑了总纵弯曲的轴向应力和局部应力的影响。Mansour（1997）[7]等通过船体梁、板格和加筋板三种不同失效模式，给出不同失效模式下的可靠性指标。Paik（1998）[8]通过建立油船和散货船的腐蚀模型，研究了腐蚀对船体极限强度可靠性的影响。Guedes Soares（1999）[9]则同时考虑腐蚀和疲劳，研究了两者对于结构可靠性模型的影响。在国内，桑国光（1986）[10]对可靠性方法进行了系统的论述，并针对船体结构屈服失效模式，提出了船体梁的载荷和承载能力的概率分布。祁恩荣（2003）[11]基于改进的Rosenbluthe法研究了完整船和破损船的极限强度的可靠性方法。

值得注意的是，以上研究成果大多未考虑弯扭耦合对于船体结构剩余强度的影响。本文在前人研究的基础上，对组合变形理论进行扩展，建立弯扭耦合方程，并提出了相应的可靠性评估方法。

1 破损船体组合变形

船体极限状态下的组合变形也可用向量模及其与三个轴的方向角进行表示：

其中：θ1的方向角。

从船体组合变形的角度，根据Guedes Soares[12]对于组合弯矩的耦合方程进行扩展，考虑扭转变形项，建立了弯扭耦合方程，如（4）式。利用有限元软件ABAQUS模拟组合变形下结构的极限状态，确定破损工况下船体的弯扭耦合方程。

其中：Mx为水平弯矩，My为垂向弯矩，Mz为扭矩。Muy为垂向极限弯矩；Muz为水平极限弯矩；Mux为极限扭矩；αi（ i=1，2，3）为结构耦合系数，其范围为 ［1.0，2.0］。

2 破损船体载荷计算

船体破损将会引起船舶浮态的变化。考虑船体受损重量损失和船体进水，根据符拉索夫参数即通过平均吃水T、横倾角φ和纵倾角φ三个浮态参数来确定船舶的浮态。

破损船舶浮态方程：

其中：P为重力；D为浮力；γ为重度；△为破损舰船排水体积；浮心坐标 （xB，yB，zB）；重心坐标 （xG，yG，zG）。通过方程（5）即可求解船体的浮态。再根据三维频域势流理论[13]，计算出破损船体的波浪载荷响应函数H （ω ，V）。

2.1 破损舰船波浪弯矩的短期分布

在短时间内，海浪可认为是均值为0的平稳正态随机过程。对线性波浪载荷情况，海浪波浪载荷所对应的随机过程亦将是均值为0的平稳正态的。在波浪载荷线性响应系统下，波浪载荷的谱密度与海浪谱密度的关系如下：

其中：Sζ（ω ，H1/3，Tz）为海浪谱密度；SW（ω，H1/3，Tz，V ）为波浪载荷的谱密度；H （ω ，V ）为系统传递函数的模；ω为波浪圆频率，V为航速，H1/3为有义波高，Tz为波浪的特征周期。

同时假定波浪载荷为窄谱，故幅值X短期响应服从Rayleigh分布，其概率密度和分布函数如下：

其中：方差σ2求得：

2.2 破损舰船波浪弯矩的救援期分布

破损舰船救援期分布，依据船体波浪载荷的长期分析，将短期分析结果按（9）式和（10）式加权组合。假设破损舰船在不考虑航速V变化情况下，每一波浪载荷短期分布的概率函数是在特定的航向、海况条件下的条件概率，因此舰船波浪载荷幅值X的概率密度f（x）和分布函数F（x）应是对应的短期概率密度fw（x）和分布函数Fw（x）的加权组合：

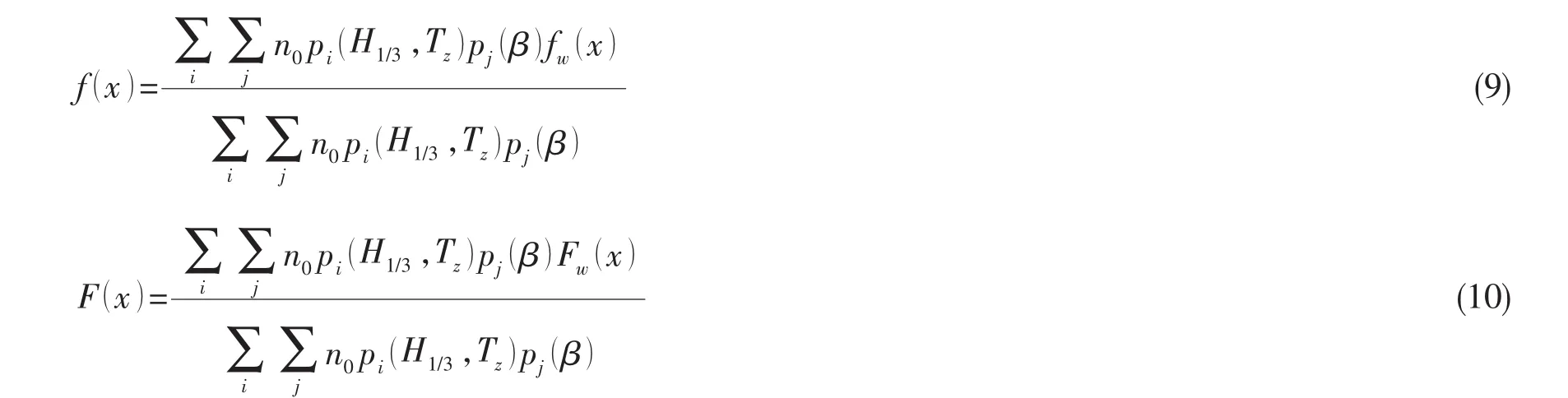
其中：n0为各短期分布中单位时间内波浪载荷循环数；pi（ H1/3，Tz）为海况出现概率；pj（β）为航向角出现概率。

3 破损舰船剩余强度评估方法

船体结构受环境载荷、结构形式、材料性能等主客观因素的影响，使得结构响应具有不确定性。考虑到外载荷与结构承载能力的不确定性，采用可靠性评估方法更加符合舰船航行的实际情况。

在结构抗力强度上，由于屈服极限和材料厚度等不确定性因素符合正态分布，故假定船体的极限弯矩和扭矩符合正态分布，根据Rosenbluthe法计算其特征参数。而船体外载荷方面，认为静水载荷为常值，主要考虑波浪载荷的影响。可靠性评估方法采用改进后的验算点方法，具体步骤如下：

根据弯扭耦合方程，确定极限状态函数：

其中：垂向、水平和扭转载荷弯矩幅值分别为Xi（i=1，2，3）；而垂向、水平和扭转结构承载能力的幅值分别为Xi（i=4，5，6）。

由于载荷分布是非正态分布，故在验算点P*处与正态分布拟合，使得实际的分布与正态分布的概率密度函数和分布函数都相等，从而得到等效正态变量的均值和方差：

等效后的载荷幅值Xi（i=1，2，3）和结构承载能力的幅值Xi（i=4，5，6）都为正态随机变量，联立方程（14）和（15），使用数值逼近的方法求得可靠性指标β，进而求得结构的失效概率。

其中：方向余弦cosθXi为

参照LR规范，破损舰船在救援期遭遇80%海况下的结构失效概率小于5%视为满足船体结构剩余强度的评估要求。

4 算 例

本文应用上述方法对一条钢质海船进行了剩余强度评估。该船总长241m，型宽32 m，型深17.5 m，满载设计吃水10.8m。由于船中剖面所受载荷较大，故作为本文主要考察的对象。为了有效模拟周围结构对船舯剖面的作用，将危险剖面沿船长前后延长至结构强支撑构件处。船宽方向取全船宽，型深范围内从甲板上缘向下伸至外底。参照LR规范对搁浅和触礁中破损状态的规定，确定破口尺寸为宽5 m，高至内底板下。有限元模型如图1。

调整方向角θi（i=1，2）来控制组合变形，每旋转10°对破损船体的剩余承载能力计算一次。表1列出了方向角每旋转30°的剩余承载能力值。根据最小二乘法的原理得到结构耦合系数，从而确定破损船的弯扭耦合方程，具体系数值见表2。

图1 破损船体有限元模型示意图Fig.1 Finite elementmodelofdamaged ship

表1 船体剩余承载能力有限元计算结果Tab.1 Results of residual bearing capacity by finite element calculation

表2 结构耦合系数Tab.2 Structuralcoupling coefficient

弯扭耦合方程第一象限内空间示意图以及其XOY、YOZ、ZOX平面截面线与有限元计算值对比如图2。

根据其材料的屈服极限和板材的厚度服从正态分布，其变异系数分别为0.08和0.03，由Rosenbluthe法计算出其特征参数[14]如表3。波浪载荷则是采用北大西洋海浪谱中80%的海况计算载荷的特征参数值，具体见表4。

表3 结构极限承载能力特征值统计（单位：108NM）Tab.3 Statisticalcharacteristics of structural ultimate bearing capacity

图2 弯扭耦合方程示意图（单位：108NM）Fig.2 Interaction equation on bending-twist coupling effect

表4 波浪载荷特征值统计（单位：106NM）Tab.4 Statistics of wave load eigenvalue

根据结构承载能力和载荷特征值，计算破损舰船结构失效概率，见表5。其中考虑弯扭耦合影响下船体剩余强度的评估方法记为方法一，将单独考虑垂向弯矩的船体剩余强度的评估方法记为方法二。由表5可知，在搁浅破损的状态下，船体的失效概率小于5%，船体结构较为可靠。通过对比两种方法中各个浪向下船体结构的失效概率，发现迎浪工况下失效概率最高，考虑弯扭耦合影响下的失效概率将有所升高。其中在斜浪30°工况下，失效概率升高0.067%，升高值最大。

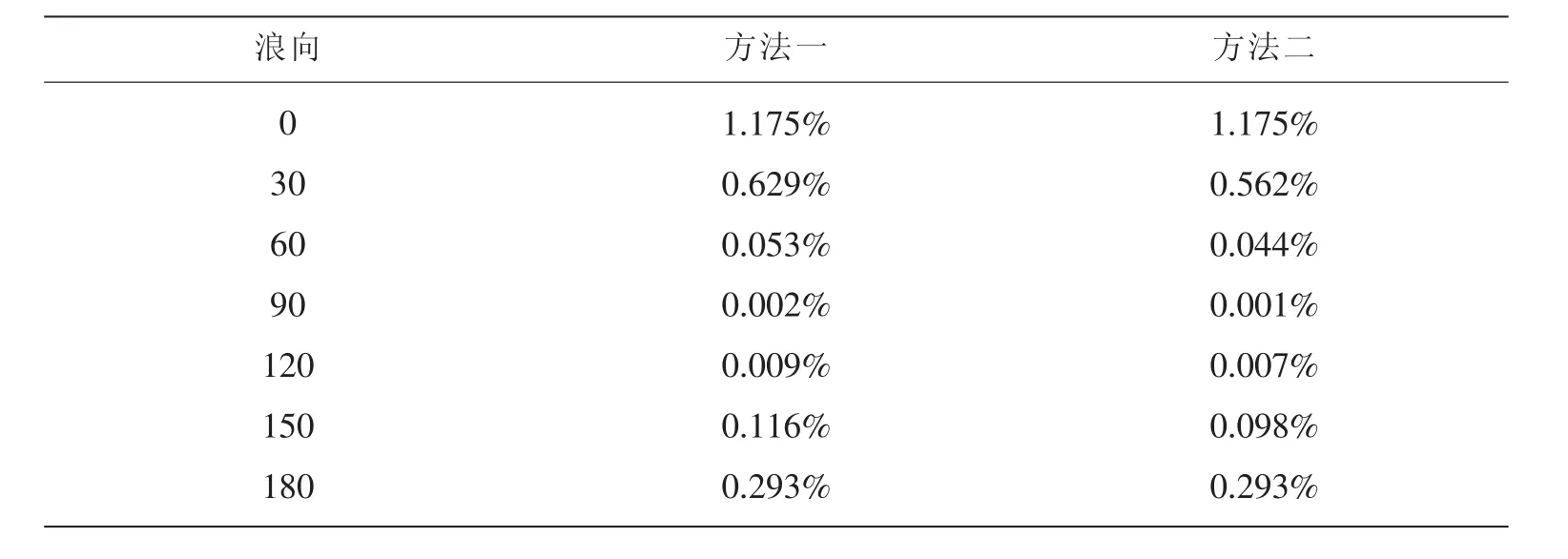
表5 破损船结构失效概率Tab.5 Failure probability of ship structure

5 结 论

本文通过有限元法计算组合变形下船体的承载能力，确定弯扭耦合方程。并在此基础上，建立了考虑弯扭耦合影响下船体剩余强度的评估方法。

（1）通过算例可知船体在破损后的救援期间失效概率较小，满足本文的破损船剩余强度要求。

（2）破损舰船在迎浪下结构的失效概率较高。虽然在斜浪工况中载荷的垂向弯矩减小，水平弯矩和扭矩也有所增大，但由于垂向弯矩在载荷中成分占比例较高，仍是引起结构失效的主要原因。

（3）斜浪工况下，考虑弯扭耦合影响下的船体结构失效概率将有所升高且其值不容忽视。因此，有必要在船体设计初期考虑弯扭耦合影响下的船体剩余强度。

[1]ABS.Guide for dynamic based design and evaluation of bulk carrier structures[S].1995.

[2]DNV.Hull structural design ship with length100meters and above[S].1997.

[3]Lloyd’s Register.Provisional rules for the classification of naval ships[S].1999.

[4]Paik J K,Thayamballi A K,Yang S H.Residual strength assessment of ships after collision and grounding[J].Marine Technology,1998,35：38-54.

[5]Guedes Soares C,et al.Reliability based ship structural design[C].Trans SNAME,1996,104：357-389.

[6]Wang X,Jiao G,Moan T.Analysis of oil production ships considering load combination,ultimate strength and structural reliability[C].Trans SNAME,1996,104：3-30.

[7]Mansour A E,Wirsching P H,Lucket M D,et al.Structural safety of ships[C].Trans SNAME,1997,105：61-98.

[8]Paik J K,Thayamballi A K,Kim S K.Ship hull strength reliability considering corrosion[J].Journal of Ship Researeh,1998,42(2)：154-165.

[9]Guedes Soares C.Reliability of corrosion protected and maintained ship hulls subjected to corrosion and fatigue[J].Journal of Ship Researeh,1999,43(2)：65-78.

[10]桑国光.应用结构可靠性原理研究船舶纵弯曲强度[J].中国造船,1986(4)：102-123.Sang Guoguang.Application of structuralreliability theory to ship longitudinal strength[J].China Shipbuilding,1986(4)：102-123.

[11]祁恩荣.完整和破损船体极限强度可靠性研究[D].无锡：中国船舶科学研究中心,2003.QI Enrong.Ultimate strength reliability analysis of intact and damaged ships[D].Wuxi：China Ship Scientific Research Center,2003.

[12]Guedes Soares C.Interaction equation for the collapse of tankers and containerships under combined bending moments[J]. Journal of Ship Researeh,1997,41(3)：230-240..

[13]船舶在波浪中的运动的势流理论[M].北京：国防工业出版社,2008.

[14]李陈峰.破损舰船剩余强度评估方法研究[D].哈尔滨：哈尔滨工程大学,2009.Li Chenfeng.Residual strength assessment of damaged warship[D].Harbin：Harbin Engineering University,2009.

Residual strength assessment method of damaged ships based on bending-twist coupling effect

TANG Hao-yun,REN Hui-long,WAN Qian,LI Chen-feng,FENG Guo-qing
(College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China)

The residual strength of damaged ship structure is an important indicator of structural design. The method on the residual strength mainly considers the vertical bending moment and ignores the influence of the combined deformation in oblique waves.In this paper,the method on the residual strength of the damaged ship is studied.The interaction equation on bending-twist coupling effect for damaged ship under the combined deformation is derived.The structural coupling coefficients are determined by NFEM method. The reliability assessment methods of damaged ship on residual strength are established with considering the bending-twist coupling effect.

residual strength;structure strength;NFEM method(nonlinear finite element model);reliability

U661.43

A

10.3969/j.issn.1007-7294.2017.07.007

1007-7294（2017）07-0856-08

2016-12-27

国防课题基金资助项目（51414030204CB0101）

唐浩云（1989-），男，博士研究生，E-mail：conanthy@126.com；

任慧龙（1965-），男，教授，博士生导师。