新型水轮机聚能导流结构的设计与参数优化
2017-08-01李龙敬周慎杰
李龙敬,周慎杰
(山东大学 机械工程学院,山东 济南 250061)
新型水轮机聚能导流结构的设计与参数优化
李龙敬,周慎杰
(山东大学 机械工程学院,山东 济南 250061)
文章以提高叶片姿势可变的水轮机获能能力为目的,结合水轮机的运动规律,提出了一种新的三段式聚能导流结构,借助数值模拟的方法,对不同参数的NACA翼型的增速效果进行了研究,确定了聚能导流结构的具体结构形式。通过改变影响聚能导流结构水动力学性能的几个重要参数,综合实际应用得到了水动力学性能较优的聚能导流结构,确定了导流结构的安装参数和结构参数。
翼型;聚能导流结构;增速比
0 引 言
通常潮流能水轮机的获能效率在25%到30%之间[1],相对风力发电,整体获能效率较低,为了最大限度地获取潮流的动能,在潮流能获能机构外部增加聚能导流结构是提高获能效率的有效方法之一,同时导流结构还能起到支撑体的作用,将水轮机固定在工作海域内。因此,国内外不少学者和科研机构都在致力于聚能导流结构的研究[2-3]。
陈晗[4]在对弹簧控角竖轴直叶片水轮机的实验研究中,提出了凹形聚能导流结构和凸形聚能导流结构两种结构,通过实验研究发现凹形聚能导流结构水轮机的获能效率要高于凸形聚能导流结构的水轮机。孙科[5,8-9]借鉴风力机扩散器的理论,设计了一种对称式的导流结构,提出了S型、W型等多种线型结构,借助数值模拟的方法对不同的线型结构的性能进行了分析;提出了设计聚能导流结构扩张门方案,通过研究扩张门不仅可以提高罩内流速,而且还有利于提高流场内的稳定性。刘斌[6]通过非定常涡面元法对加装聚能导流结构水轮机的水动力性能进行理论计算,分析了水动力机理,得出聚能导流结构几何参数和安装位置对于轮机水动力性能的影响规律。王树杰[7]针对柔性叶片的水轮机设计了一种中心对称式的导流结构,通过改变影响聚能导流结构性能的几个重要参数,对聚能导流结构的水动力学性能进行了数值模拟,得出了水动力学性能较优的导流结构。
加拿大的Faure和Pratte[10]提出在河道内垂直轴水轮机上安装聚能导流结构的想法,通过聚能导流结构的引流作用改变水流冲击水轮机的角度和速度,解决低流速时水轮机获能效率偏低的问题。他们研究了聚能导流结构入流角度、叶轮密实度、叶片与聚能导流结构之间的缝隙等因素对水轮机获能效率的影响。
我们在对新型水轮机的前期研究中,设计了叶片姿势可变的潮流能获能水轮机,并对水轮机的水动力学性能进行了研究,已经取得了阶段性的成果[11]。为了进一步提高水轮机的获能效率,根据水轮机自身的运动特点,提出了一种新型的三段式导流结构,并对不同翼型导流结构的增速效果进行了研究,确定了增速段的NACA翼型结构,并针对不同的安装参数和结构参数进行了数值计算,确定了聚能导流结构的具体参数。
1 聚能导流结构的设计
流体在流动过程中沿流动方向作用于固体壁面的总力称为曳力,而固体壁面在流动方向对流体的反作用力称为流体阻力。对于绕流流动,流体作用与固体壁面的力一般可分为正压力和切应力两部分。相应地,固体壁面的反作用力也由形状阻力和摩擦阻力两部分构成。其中,形状阻力是固体壁面上正压力分布不均所产生的,又称压差阻力;而摩擦阻力则是固体壁面上切应力分布不均所产生的。因此在导流结构的设计当中要尽可能减小流体阻力,从而最大限度地获取潮流的动能。
1.1 聚能导流结构的确定
如图1所示,根据水轮机自身运动规律,聚能导流结构的设计应该保证两侧来流时都有明显的增速效果,且左侧来流时,叶片从正上方打开,水轮机的主增速区域应处于转子正上方,根据流体力学的理论,当流体流过曲面物体时,沿曲面方向的速度是改变的,所以考虑采用凹面的结构会使流体沿切线方向向上运动,使转子上方的增速效果明显。当从右侧来流时,叶片从正下方打开,水轮机的主增速区域应处于转子正下方,同样基于流体力学的理论,采用凸面结构使流体沿着曲面的切线方向流动,从而达到了转子下放流速增大的目的。

图1 聚能导流结构和水轮机示意图Fig.1 The diagrammatic sketch of diffuser and turbine
基于上述考虑,拟采用单侧三段式结构,根据每段的特点,分别命名为凹面增速段、过渡段和凸面增速段。
人们在以前的研究中,凹面增速段大多采用圆弧结构。由于圆弧的变化形式单一,导流后对水流的增速作用不够强,不便于最大限度地获取潮流的动能。为进一步提高导流结构的增速能力,我们借鉴NACA翼型结构,提出了在凹面增速段采用NACA翼型导流结构,并与之前的圆弧导流结构进行对比分析。
由于凹面增速段与凸面增速段无法直接相连,故考虑采用圆弧的过渡结构连接两部分,即过渡段。
在凸面增速段的结构设计上,结合流体力学知识,当流体绕弯曲壁面流动时,为了尽可能地减小流动阻力,需保证过渡段与凸面增速段相切,故凸面增速段优先考虑圆弧结构。
NACA翼型是美国国家航空咨询委员会(NACA)开发的一系列翼型。每个翼型的代号由“NACA”这四个字母与一串数字组成,将这串数字所描述的几何参数代入特定方程中即可得到翼型的精确形状。NACA四位数字翼型是美国NACA最早建立的一个低速翼型系列,与早期的其他翼型相比,有较高的最大升力系数和较低的阻力系数。在每个翼型代号NACA XYZZ中,后面四位数字的含义是:X—相对弯度;Y—最大弯度位置;ZZ—相对厚度。例如,NACA2412表示翼型的相对弯度为2%,最大弯度位置在弦长的0.4,相对厚度为12%。主要的翼型结构如表1所示。

表1 不同的翼型结构Tab.1 Different kinds of airfoil profile
本文分别对不同相对弯度、不同的最大弯度位置和不同的相对厚度进行研究,然后取最优结果与圆弧型迎流面进行比较。
1.2 主要参数
聚能导流结构的参数主要分为安装参数和结构参数两部分。安装参数主要包括聚能导流结构在高度方向上与水轮机转子中心的相对位置h和水平方向上与水轮机转子中心的相对位置e;结构参数根据实际情况主要考虑凹面增速段高度H和凸面增速段圆弧半径R。
凹面增速段高度H:由于增速段采用翼型结构,翼型的高度与长度是成对应关系的,翼型高度确定后,其长度也是确定的,所以对于增速段只需要考虑翼型的相对厚度即可确定增速段的结构。
凸面增速段圆弧半径R:对于凸面增速段结构,首先从结构设计角度凸面增速段的圆弧要与过渡段的圆弧满足相切的关系,所以凸面增速段的圆心相对位置是确定的,由于增速段高度已经确定,所以凸面增速段结构的高度也确定,通过改变不同的圆弧半径,即可得到不同的凸面增速段的长度,可通过研究不同的圆弧半径下聚能导流结构的增速效果来确定凸面增速段圆弧半径。
2 水动力学特性的数值模拟
从优化导流结构来说,水轮机的转动并不会对增速效果有很大的影响,反而是水轮机转动的网格处理与计算量加大了模拟的复杂程度与难度,所以在模拟过程中考虑放置一静止状态的水轮机对不同形式的导流结构的增速效果进行对比,选出最优的导流结构。
2.1 数值模拟方法
基于Fluent软件稳态计算方法,进行聚能导流结构在敞水状态下的水动力性能模拟。如图2所示。计算区域:流场计算域以转子中心为基准,转子直径2R为100mm,设置前方区域10倍于转子直径,后方10倍于转子直径,上取6倍于转子直径的矩形形区域,下到聚能导流结构的下侧边缘。
网格划分:整个流场区域采用结构化网格结构,在靠近聚能导流结构的壁面区域增加网格密度,而在聚能导流结构外围则适当放宽网格尺寸,以减小数值模拟的运算量。整个计算区域的网格数量为20 989。
边界条件:定义为左侧为流场入口,入口速度为1 m/s,边界类型为速度入口(velocity-inlet);右侧为流场出口,边界类型为压力出口(pressure-outlet);流场上下边界、聚能导流结构和转子的壁面均采用无滑移壁面(wall)。
针对聚能导流结构流线型较好的特点,数值仿真中选用k-ω湍流模型;时间步长为0.01s,迭代步数为1 500。
2.2 网格无关性验证
在模拟过程中,网格的疏密程度会直接影响计算结果的准确性。分别对导流罩内流场进行不同疏密程度的网格划分,得到的网格数分别为10 388、20 989、30 660和43 311。
结果如表2所示,将网格数为1万与2万的相比其改变量大于3%,而2万与3万和4万相比,改变量均小于3%。考虑到网格数越多,计算时间越长,为了提高计算效率,采用了2万网格的加密方式对流场区域进行网格划分。

图2 模拟流场模型Fig.2 Fluid domain model

表2 不同单元尺寸下的增速比Tab.2 Speed increasing ratio under different element size
2.3 模拟有效性的验证
利用数值模拟的计算方法对流体结构进行设计与参数优化是目前国内外流体力学领域普遍采取的一种基本方法,计算结果也大都在后续的实验中得到了有效的验证。在前面引言中已经提到的陈晗、孙科、王树杰等均采用数值模拟的方法对不同类型的导流结构进行了研究,取得了一定的成果。本文也采用相类似的数值模拟方法,对新提出的三段式聚能导流结构进行了参数优化。
孙科[5]在论文中结合对水轮机的实验数据对几种导流结构模型进行了数值模拟,计算结果已得到业内专家的广泛认可。采用与本文数值研究相同的模拟方法,对孙科提出的有关导流结构的3种模型进行了数值计算,并与孙科论文中的原模拟结果进行了对比,本次模拟结果与孙科论文中的模拟结果相吻合,误差率均在3%以内。由此可见,本文所采用的模拟方法是有效的。详见表3。

表3 导流罩模型内的最大流速(m/s)Tab.3 The maximum velocity of dome models(m/s)
3 数值结果分析
考虑通过引入增速比来评定聚能导流结构的增速效果。
由于水流从两侧来流时主要的增速区域有一定的区别,所以以转子中心为原点,左侧来流时,取转子上方55 mm到95 mm的范围得到该区间的瞬时速度,然后对速度取平均值,计算出转子上方的瞬时平均流速,然后再除以来流速度,得到水轮机上方的增速比。取转子下方55 mm到75 mm的范围得到该区间的瞬时速度,然后对速度取平均值,计算出转子下方的瞬时平均流速,然后再除以来流速度,得到水轮机下方的增速比。右侧来流时,取转子上方55 mm到75 mm的范围得到该区间的瞬时速度,然后对速度取平均值,计算出转子上方的瞬时平均流速,然后再除以来流速度,得到水轮机上方的增速比。取转子下方55 mm到95 mm的范围得到该区间的瞬时速度,然后对速度取平均值,计算出转子下方的瞬时平均流速,然后再除以来流速度,得到水轮机下方的增速比。
本文通过对不同翼型的聚能导流结构进行数值模拟,结合数值模拟结果分析确定最优的翼型结构;在此基础上再对聚能导流结构进行参数优化,确定最优的安装参数和结构参数。
3.1 凹面增速段结构的确定
3.1.1 不同参数NACA翼型结构的数值模拟结果
在模拟中固定增速段高度为2.2R,图3和图4是聚能导流结构在不同相对弯度(NACA2215、NACA4215、NACA5215和NACA6215)下的增速效果。随着相对弯度的增大,充分利用翼型曲面对流场的干扰,改变了流体的运动轨迹,起到了更优的引流作用,使得转子正上方的流速进一步增大,当增加到一定程度后,弯度过大会导致聚能导流结构的迎流面对流体的运动形成阻碍作用,所以聚能导流结构的增速比呈现先大后小的过程,故NACA4215的翼型结构增速效果更佳。根据翼型的代号规则确定翼型相对弯度为4。

图3 不同相对弯度下左侧来流时聚能导流结构上方增速比Fig.3 Speed increasing ratio above diffuser under different relative curvature in case of incoming flow on the left

图4不同相对弯度下左侧来流时聚能导流结构下方增速比Fig.4 Speed increasing ratio below diffuser under different relative curvature in case of incoming flow on the left
图5 和图6是不同相对厚度(NACA4206、NACA4212、NACA4215和NACA4221)下聚能导流结构的增速效果,从图中可以看出,随着相对厚度的增加,针对固定高度的导流结构,相当于增速段的长度由长变短,当长度过长时,阻力形式主要为摩擦阻力,但过于平缓增速效果不佳,随着长度变短,阻力形式以压差阻力为主,对流体的阻碍作用慢慢增大,聚能导流结构的增速效果呈现了迅速增加到快速下降然后趋于平缓的过程,对比可以看出NACA4212翼型结构的增速效果更佳。根据翼型的代号规则确定翼型相对厚度为12。

图5 不同翼型厚度下左侧来流时聚能导流结构上方增速比Fig.5 Speed increasing ratio above diffuser under different airfoilthickness in case ofincoming flow on the left

图6 不同翼型厚度下左侧来流时聚能导流结构下方增速比Fig.6 Speed increasing ratio below diffuser under differentairfoilthickness in case ofincoming flow on the left

图7 不同最大弯度下左侧来流时聚能导流结构上方增速比Fig.7 Speed increasing ratio above diffuser under different circle radius in case of incoming flow on the left
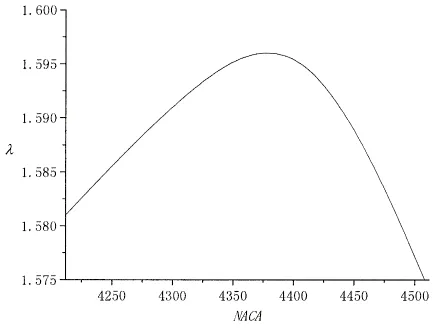
图8不同最大弯度下左侧来流时聚能导流结构下方增速比Fig.8 Speed increasing ratio below diffuser under different circle radius in case of incoming flow on the left
图7 和图8是不同最大弯度(NACA4212、NACA4312、NACA4412和NACA4512)下聚能导流结构的增速效果。从图中可以看出随着最大弯度的变大,相当于改变了翼型曲面的弯曲程度,会改变曲面对流场的干扰作用,引起转子上方流速的变化,增速比呈现先下降后逐渐增大的趋势,聚能导流结构下方的增速比呈现先增大后逐渐下降的趋势,在这个变化过程中聚能导流结构的主作用增速区域发生了变换,综合聚能导流结构上下的增速比考虑采用NACA4212的翼型结构。根据翼型的代号规则确定翼型最大弯度位置为2。
3.1.2 圆弧结构的数值模拟结果
给定相同的凹面增速段高度与长度参数,对采用不同圆弧半径的导流结构进行数值模拟,根据图9和图10,可以得到在半径为300时,聚能导流结构有更佳的增速效果,导流结构上方增速比为1.531,下方增速比1.518。

图9 不同圆弧半径下左侧来流时聚能导流结构上方增速比Fig.9 Speed increasing ratio above diffuser under different airfoil thickness in case of incoming flow on the left

图10 不同圆弧半径下左侧来流时聚能导流结构下方增速比Fig.10 Speed increasing ratio below diffuser under different airfoil thickness in case of incoming flow on the left
3.1.3 翼型凹面增速段与圆弧型凹面增速段的增速分析
由表4可以看出,NACA4212翼型结构的增速效果优于圆弧结构,故增速段结构应采用NACA4212的翼型结构。

表4 不同线型的增速比Tab.4 Speed increasing ratio under different linetypes
3.2 安装参数—长度方向上不同的安装距离e
安装参数主要考虑聚能导流结构在高度方向上和长度方向上与水轮机的相对位置。考虑让聚能导流结构的内壁与水轮机叶片完全张开时的轨迹相切,故聚能导流结构在高度方向上与水轮机的相对位置可以直接确定,在水平方向上的距离e要通过模拟得到。图11为聚能导流结构安装位置参数示意图。
取R=50,结合实际考虑取安装距离分别为0.6R、0.8R、1R、1.2R、1.4R、1.6R和1.8R七种工况,采用控制变量法进行研究。数值模拟结果如图12-15所示。随着聚能导流结构在长度方向上的安装距离e从大到小不断变化,聚能导流结构上下方的平均增速比呈现先增大后减小的过程。当聚能导流结构的顶点位置距离水轮机转子中心位置一个R的距离时,平均增速比达到最大值。随着安装位置的移动,聚能导流结构下放的增速比变化趋势更为明显,当聚能导流结构逐渐靠近水轮机转子后,转子上下均有较好的增速效果。

图11 聚能导流结构的安装位置参数Fig.11 The installation parameters ofdiffuser

图12 不同安装位置e下聚能导流结构上方的增速比Fig.12 Speed increasing ratio under different installation sites

图15 安装位置为1.8R时的速度矢量图Fig.15 The velocity vector when installed at location of 1.8R
3.3 结构参数
结构参数如图16所示,根据翼型结构的特点以及设计的原则,主要参数包括凹面增速段高度H和凸面增速段圆弧半径r。
3.3.1 不同高度H下聚能导流结构的增速效果分析
考虑研究不同高度下的NACA4212的结构,探究增速段高度对导流增速效果的影响。取2.2R、2.6R、3R和3.4R四种情况进行分析。模拟结果如图17和图18所示。随着聚能导流结构高度的增加,聚能导流结构对流场的干扰作用发生了改变,对水流的阻碍作用由摩擦阻力变成压差阻力,聚能导流结构上方增速比会逐渐增大然后慢慢减小并趋于平缓;而聚能导流结构下放增速比一直处于逐渐增大的过程,转子下方流速明显增大,但转子上方的流速相对减小,这是聚能导流结构整体结构的增大与转子相对大小综合作用的结果。综合考虑增速效果与成本,考虑选用高为2.6R的导流结构。
3.3.2 不同半径r聚能导流结构的增速效果分析
考虑水流从右侧流过时,研究圆弧半径对聚能导流结构增速效果的影响。分别取4.5R、5R、5.5R、6R、8R和10R六种不同的圆弧半径,模拟结果如图21所示,随着半径的不断增大,聚能导流结构本身对于水流的阻碍作用会相对减小,增速比会逐渐增大,但是当聚能导流结构凸面增速段圆弧半径增大到6R后,随着半径的再度增大,增速效果会逐渐减小然后趋于平缓,这是因为随着半径的进一步增大,聚能导流结构的凸面增速段越接近于直线结构,圆弧对流场几乎起不到干扰作用,增速效果也逐渐趋近于直线结构。

图16 聚能导流结构的结构参数Fig.16 The structure parameters of diffuser

图17 不同高度H下聚能导流结构上方的增速比Fig.17 Speed increasing ratio above diffuser under different H

图18 不同高度H下聚能导流结构下方的增速比Fig.18 Speed increasing ratio below diffuser under different H

图19 高度为2.6R时速度矢量图Fig.19 Velocity vector atthe heightof2.6R

图20 高度为3.4R时速度矢量图Fig.20 Velocity vector at the heightof3.4R
4 结 论
本文根据新型水轮机运动特点,以新型水轮机聚能导流结构为研究对象,提出了新型三段式聚能导流结构,通过数值模拟的方法确定了增速段NACA翼型结构选型,对影响聚能导流结构的主要参数进行了优化研究,得出以下结论:
(1)本文首次对NACA翼型结构的增速效果进行了研究,通过对不同参数的翼型结构进行数值计算,确定选用NACA4212的翼型作为凹面增速段结构。根据模拟结果,NACA4212的翼型结构聚能导流结构上方增速比为1.591,下方增速比为1.581,比同样条件下采用圆弧型聚能导流结构的增速比分别提高了3.92%和4.15%。
(2)在增速段选用翼型结构的基础上进行结构参数优化,根据翼型结构的特点,增速段的高度与长度成比例关系,故选取不同的增速段高度作为优化参数进行优化,最终得到聚能导流结构的凹面增速段的高度为2.6R;考虑到水流从右侧来流的增速效果,针对右侧凸面增速段圆弧确定的结构特点,选取了圆弧半径作为优化参数,最终确定凸面增速段的圆弧半径为6R。
(3)根据水轮机的运动特点,考虑让聚能导流结构的内壁与水轮机叶片完全张开时的轨迹尽量相切,故聚能导流结构在高度方向上与水轮机的相对位置可以直接确定,因此选取了竖直方向上的距离e作为优化参数进行优化,确定了聚能导流结构凹面增速段与过渡段连接处与叶片姿势可变水轮机转子之间水平方向的距离为R。

图21 右侧来流时不同半径下聚能导流结构下方的增速比Fig.21 Speed increasing ratio below diffuser under different radius in case of incoming flow on the right
参考文献:
[1]余 寅,唐宏德,郭家宝.中国可再生能源发展前景分析[J].华东电力,2009,37(8):1306-1038.Yu Yin,Tang Hongde,Guo Jiabao.Developing prospect analysis of renewable energy resources in China[J].East China Electric Power,2009,37(8):1306-1038.
[2]Cresswell N W,Ingram G L,Dominy R G.The impact of diffuser augmentation on a tidal stream turbine[J].Ocean Engineering,2015,108(12):155-163.
[3]Daniele E,Coiro D P.Optimization of diffuser geometry for an horizontal axis shrouded hydro turbine[C].International Conference on Clean Electrical Power.IEEE,2013:240-247.
[4]陈 晗.弹簧控角竖轴直叶水轮机水动力性能研究[D].哈尔滨:哈尔滨工程大学,2006.Chen Han.On study of hydrodynamic performance of the spring-controlling of vertical-axis variable-pitch turbine[D]. Harbin:Harbin Engineering University,2006.
[5]孙 科.竖轴H型叶轮及聚能导流结构流体动力性能参数模拟[D].哈尔滨:哈尔滨工程大学,2008.Sun Ke.Numerical simulation on fluid dynamic performance of h-shaped vertical axis turbine and duct[D].Harbin:Harbin Engineering University,2008.
[6]刘 斌.带聚能导流结构的竖轴潮流水轮机水动力性能研究[D].哈尔滨:哈尔滨工程大学,2007.Liu Bin.Study on the hydrodynamic performance of vertical-axis turbine with demos[D].Harbin:Harbin Engineering U-niversity,2007.
[7]鹿兰帅.潮流能驱动的柔性叶片水轮机水动力性能试验研究[D].青岛:中国海洋大学,2009.Lu Lanshuai.Experimental study on hydrodynamic performances of flexible blade turbine driven by tidal energy[D]. Qingdao:Ocean University of China,2009.
[8]张 亮,孙 科,罗庆杰.潮流水轮机聚能导流结构的水动力设计[J].哈尔滨工程大学学报,2007,28(7):734-737.Zhang Liang,Sun Ke,Luo Qingjie.Hydrodynamic design of diversion cover for a tidal-stream hydro turbine[J].Journal of Harbin Engineering University,2007,28(7):734-737.
[9]荆丰梅,张 亮,张鹏远,等.潮流能发电增速聚能导流结构研究[J].哈尔滨工程大学学报,2012,33(4):409-413.Jing Fengmei,Zhang Liang,Zhang Pengyuan.Study on an accelerated diffuser of tidal current power generation[J].Journal of Harbin Engineering University,2007,28(7):734-737.
[10]Batten W M J,Bahaj A S,Molland A F,et al.Experimentally validated numerical method for the hydrodynamic design of horizontal axis tidal turbines[J].Ocean Engineering,2007,34(7):1013-1020.
[11]Li L J,Zhou S J.Numerical simulation of hydrodynamic performance of blade position-variable hydraulic turbine[J].Journal of Hydrodynamics Ser B,2017,29(2):314-321.
Design and parameter optimization of novel energy-gathered and diversion mechanism
LI Long-jing,ZHOU Shen-jie
(Shandong University School of Mechanical Engineering,Jinan 250061,China)
In order to improve the efficiency of the Blade Position-Variable Hydraulic Turbine,a threepiece energy-gathered and diversion mechanism is proposed,combined with motion law of hydraulic turbine. By means of the numerical simulation method,the accelerating effect of different parameters of NACA airfoilis studied,then the specific structure of energy-gathered and diversion mechanism is determined.A kind of energy-gathered and diversion mechanism with excellent hydraulic performance is obtained through changing severalimportantparameters.
airfoil;energy-gathered and diversion mechanism;speed increasing ratio
TB126 TK79
A
10.3969/j.issn.1007-7294.2017.07.005
1007-7294(2017)07-0832-10
2017-03-08
山东省科技开发项目(2014GGX103028)
李龙敬(1988-),男,博士研究生,E-mail:kglilongjing@163.com;
周慎杰(1958-),男,教授。
