六自由度混联机构雅可比矩阵求解及奇异位形分析

周 辉, 丁 锐, 曹浩峰, 曹 毅

(1. 江南大学 机械工程学院, 江苏 无锡 214122；2. 上海交通大学 机械系统与振动国家重点实验室,上海 200240；3. 江苏省食品先进制造装备技术重点实验室, 江苏 无锡 214122)

六自由度混联机构雅可比矩阵求解及奇异位形分析

周 辉1, 3, 丁 锐1, 3, 曹浩峰1, 3, 曹 毅1, 2, 3

(1. 江南大学 机械工程学院, 江苏 无锡 214122；2. 上海交通大学 机械系统与振动国家重点实验室,上海 200240；3. 江苏省食品先进制造装备技术重点实验室, 江苏 无锡 214122)

提出一种由2个不同的三自由度并联机构串接而成的混联机构, 针对下端和上端并联模块分别建立速度雅可比矩阵, 然后通过上下两个并联模块的运动关系, 建立整个混联机构的整体雅可比矩阵.雅可比矩阵是分析机构奇异位形的基础, 通过令机构整体雅可比矩阵行列式为零, 从而得到机构奇异的非线性方程来研究混联机构的奇异位形, 同时运用MAPLE软件绘制出机构的奇异轨迹.该方法建立了由2个并联模块组成的混联机构的雅可比矩阵, 具有一定的理论意义.

混联机构；雅可比矩阵；并联模块；奇异位形

混联机构结合了传统串联机构和并联机构的优点, 具有承载能力强、刚度大、精度高、工作空间大等优点, 有效地扩大了机器人的应用领域[1].近年来混联机构引起了学术界的关注, 但是由于混联机构构型复杂, 其理论研究仍不成熟, 严重影响了混联机构的发展[2].

雅可比矩阵在机器人的运动学分析中具有重要地位, 机器人的分离速度控制、静力分析、灵活性和可操作度分析等都要用到机器人的雅可比矩阵, 因此, 机器人雅可比矩阵的准确、快速求解显得尤为重要[3].目前，对单个并联机构的雅可比矩阵及奇异位形的研究相对比较成熟.Hunt[4]教授最先开始研究并联机构奇异性.随后Fichter[5]、Merlet[6]、Gosselin[7]、Di-Gregorio[8]、黄真[9]等学者在该领域都做出了重大研究贡献, 对于后续系统地研究机构奇异有着重要的意义[10].文献[11]对2-PRS-PRRU并联机构进行了分析, 通过所求的雅可比矩阵, 分析了机构的逆解奇异、正解奇异和混合奇异.文献[12]分析了3/6-SPS型Stewart机构奇异轨迹的解析表达式, 基于此原理提出了分析并联机构奇异位形的等效机构法.文献[13]对Stewart并联机构位于给定姿态时的位置奇异轨迹进行了系统的研究, 基于所建立的并联机构的力雅可比矩阵, 推导出该机构位于给定姿态时的三维位置奇异轨迹的3次符号表达式.文献[14]基于对偶螺旋理论, 基于约束子矩阵和运动子矩阵给出了非全对称少自由度并联机构完整雅可比矩阵的推导方法.混联机构由于机构间运动影响, 其奇异性问题更复杂, 对于研究混联机构奇异位形的文献还很少.文献[15]对2(2-UPR+SPR)串并联机构进行了研究, 建立了上下2个相同并联模块组成的混联机构的雅可比矩阵.文献[16]求解了由2个并联机构串接而成的混联机构的雅可比矩阵, 从而分析了机构的运动性能.

本文提出的混联机构由2个不同的并联机构模块串接而成, 通过构建上下两端并联模块的速度雅可比矩阵, 然后根据上下2个并联模块的运动关系, 建立整个混联机构的整体雅可比矩阵.在此基础上, 通过雅可比矩阵分析机构的奇异位形, 对机构的推广应用可提供一定的理论基础.

1 混联机构的描述

本文混联机构由2个并联机构串联起来, 每个并联机构都有3个自由度.混联机构结构图如图1所示.由图1可知, 位于混联机构下端部分的并联机构具有2条SPS支链和1条RPR支链, 其中RPR支链3个运动副相互垂直，呈R1⊥P⊥R2.上面并联机构具有2条SPS支链和1条RRR支链, 其中RRR支链的3个转动副相互垂直, 呈R3⊥R4⊥R5, R2和R3的转动轴线相互垂直.下面并联机构模块的驱动是位于3条分支上的3个移动副, 上面并联机构模块的驱动是2个位于分支上的移动副和另一条支链上中间的R4转动副.上下2个并联机构的动平台和静平台都是正三角形.

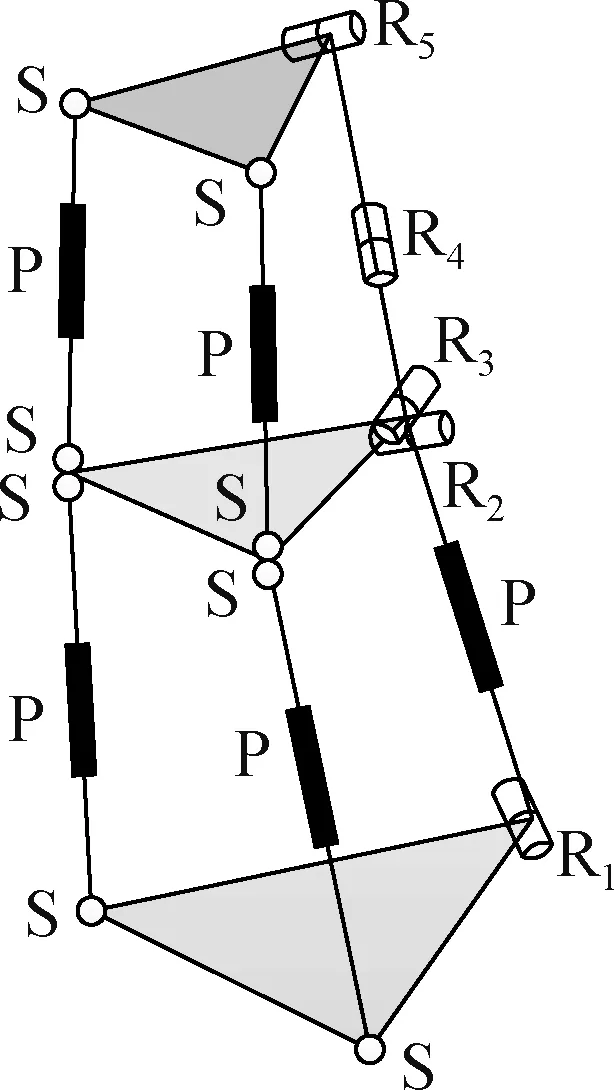
图1 混联机构结构图Fig.1 Structure diagram of the hybrid mechanism

整个混联机构的总构件数目n=15, 包括一个静平台、一个动平台、一个中间平台.运动副数目g=18, 包括8个球副S、5个移动副P、5个转动副R.由于SPS支链都可以绕着自身两端的球副旋转, 所以每条SPS支链存在一个局部自由度, 因此局部自由度数目ζ=4.运用计算空间机构自由度的Grübler-Kutzbach公式得到此混联机构的自由度[17]为

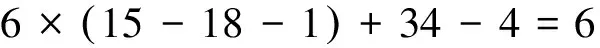
(1)

式中:fi为运动副的自由度；ν为冗余自由度.

由式(1)可知, 此双并联型混联机构具有6个自由度.

2 雅可比矩阵求解

为了进一步分析机构末端执行器与机构输入之间的速度关系, 可以求解混联机构的雅可比矩阵, 且机构的雅可比矩阵在机构奇异性分析和运动精度的分析中也具有重要作用[5].虽然雅可比矩阵是从机构速度关系中推导得到的, 但其只与机构的位形、机构类型、尺寸有关, 与机构的速度等运动参数无关, 而且雅可比矩阵是一个时变线性变换[18].

2.1 下端并联机构模块

如图2所示, 2SPS+RPR并联机构模块由静平台B和动平台m通过3条支链连接而成.静平台B是边长为a的等边三角形, 运动平台m是边长为b的等边三角形, 两平台中心点分别为O和o, 顶点分别用Ai和Bi(i=1, 2, 3)表示.

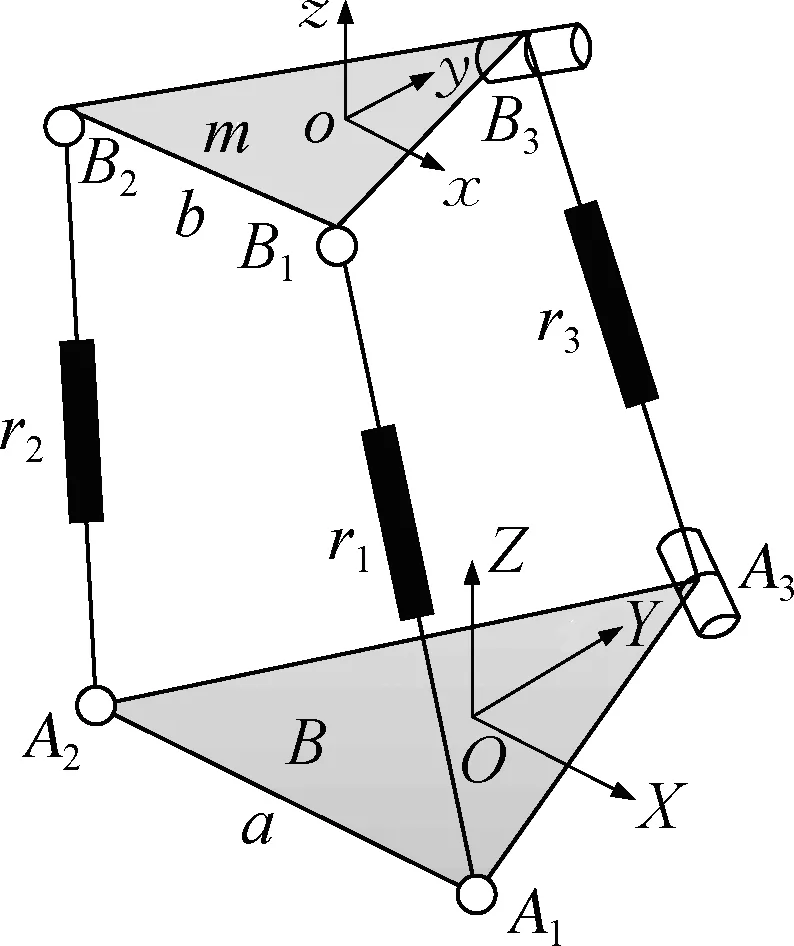
图2 下端并联模块坐标系Fig.2 Lower parallel module coordinate system

3个驱动分支包括2个SPS驱动分支r1和r2, 1个RPR驱动分支r3.2条SPS支链ri通过两端Ai点和Bi点的球副S和中间作为驱动的移动副P将静平台和动平台连接起来(i=1, 2)；RPR支链r3则通过A3点的转动副R、作为驱动的移动副P及B3点的转动副R将动平台和静平台连接起来.

如图2所示, 以机构静平台中心O为原点建立右手直角坐标系OXYZ,X轴平行于A1A2,Y轴在B面内垂直于A1A2,Z轴垂直于静平台.以机构动平台中心o为原点建立坐标系oxyz,x轴平行于B1B2,y轴垂直于B1B2,z轴垂直于动平台.

机构静平台端点在OXYZ坐标系中可表示为

(2)

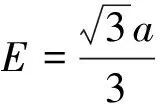
机构动平台端点在oxyz坐标系中可表示为

(3)

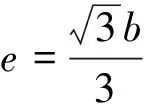
动平台各端点在坐标系OXYZ中可表示为

(4)

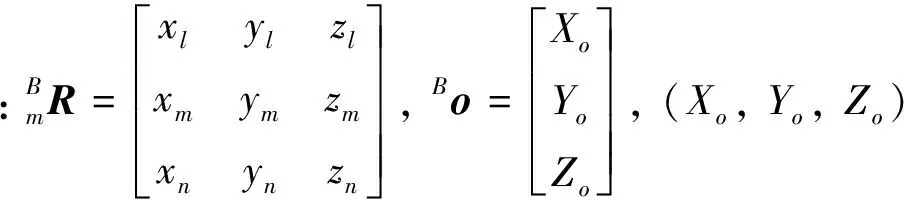
则其具体表达式为

(5)

δi表示驱动杆的单位矢量, 则δi=(Bi-Ai)/ri.由式(2)和(5)可得:

(6)

ei表示从o点到Bi点的矢量, 则ei=Bi-o, 其中,o表示点o的位置矢量.由式(5)可得:

(7)

R1表示RPR支链转动副R1在{B}中的单位矢量.R2和mR2分别表示RPR支链转动副R2在{B}和{m}中的单位矢量.

(8)

(9)

(10)

因为转动副R1和R2垂直, 则有:

R1·R2=0

(11)

将式(8)和(10)代入式(11), 则有

(12)

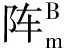
(13)

式中:sα,sβ,sγ分别表示sinα, sinβ, sinγ；cα,cβ,cγ分别表示cosα, cosβ, cosγ.

将式(4)和(13)的两种表达方式比较可得:

(14)

将式(14)代入式(12)中, 可得:

(15)

由于R1⊥P⊥R2, 所以δ3·R1=0,δ3·R2=0.将式(6)中δ3的表达式代入式(8)和(10)中可得:

eyl+X0=0

(16)

(17)

假设o到O的向量为r0, 则r0=r0[zlzmzn]T, 其中r0表示点o到O的距离.则有:

(18)

(19)

将式(19)代入式(17)中并展开, 然后将式(18)代入, 可得:

(20)

由式(2)和(5)可得各驱动杆长表达式为

(21)

式中:P0=X0xl+Y0xm+Z0xn,Q0=X0yl+Y0ym+Z0yn.

观察P0和Q0可以发现,P0=[X0Y0Z0]T·[xlxmxn]T,Q0=[X0Y0Z0]T·[ylymyn]T, 其中[X0Y0Z0]就是动平台上坐标系原点o在静坐标系OXYZ中的表达.由式(19)可得,P0=r0[zlzmzn]T·[xlxmxn]T=0, 同理Q0=0.

这样式(21)可以简化为

(22)

由式(20)可得:

(23)

由此可得：

若cβ=0, 则X0和Z0都等于零, 即动平台与静平台重合, 此时机构产生奇异, 所以cβ≠0.那么γ的表达式可写成:

(24)

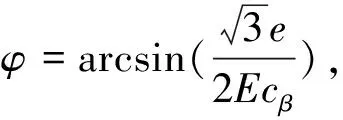
将式(19)代入式(22)中, 并将其中的γ用φ-π/3表示, 化简后得到:

(25)

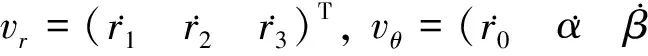
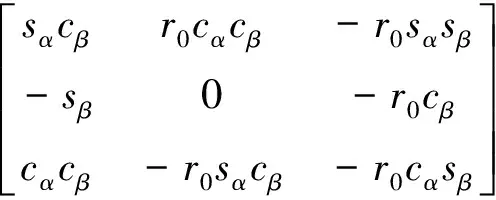
(26)

由YXZ欧拉角旋转方式对应的(Rα,Rβ,Rγ)表达形式[19]可知转动雅可比矩阵(Jω)为

(27)

所以机构的混合雅可比矩阵(Jθ)为

(28)

2.2 上端并联机构模块

2SPS+RRR并联机构如图3所示.此并联模块通过3条驱动支链连接静平台B和动平台m.上端并联模块的静平台为下端并联模块的动平台.静平台B是边长为b、中心点为O的等边三角形, 动平台m是边长为d、中心点为o的等边三角形, 两平台的三角形顶点分别用Bi和Di(i=1, 2, 3)表示.

图3 上端并联模块坐标系Fig.3 Upper parallel module coordinate system

3个驱动分支包括2个SPS驱动分支r1和r2, 1个RRR驱动分支r3.2条SPS支链rj分别通过位于支链两端Bj点和Dj点的球副S以及中间作为驱动的移动副P连接静平台和动平台(j=1, 2)；RRR支链r3则通过B3点的转动副R, 作为驱动的转动副R及D3点的转动副R将动平台和静平台连接起来, 此支链的3个转动副相互垂直.

如图3所示, 以机构静平台中心O为原点建立坐标系OXYZ,X轴垂直于B2B3,Y轴平行于B2B3, Z轴垂直于静平台.以机构动平台中心o为原点建立坐标系oxyz,x轴垂直于D2D3,y轴平行于D2D3,z轴垂直于动平台.

机构静平台端点在OXYZ坐标系中可表示为

(29)

机构动平台端点在oxyz坐标系中可表示为

(30)

式中:e为动平台中心点o到各端点的距离, 上端并

动平台各端点在坐标系OXYZ中可表示为

(31)

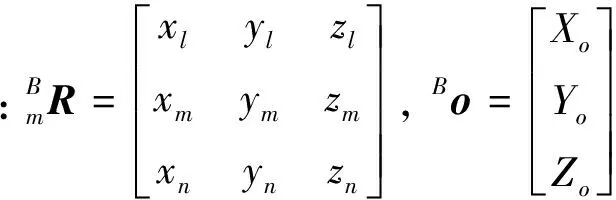
则其具体表达式为

(32)

δi表示3条支链的单位矢量, 则δi=(Di-Bi)/ri(i=1, 2, 3).由此可得:

(33)

由2SPS+RRR机构中各转动副的方位, 可得第3条支链的3个转动副对静平台坐标系的矢量为

(34)

由于R1、R2、R3相互垂直, 因此这3个矢量相互点乘结果均为0.

(35)

R1·B2B3=0

(36)

由式(35)和(36)可得:

yl=0

(37)

(38)

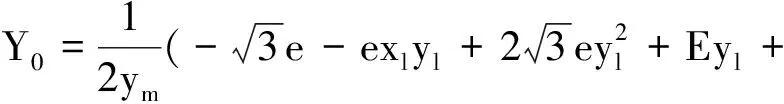
(39)

把式(37)代入式(38)和(39)中可得:

(40)

采用XZY欧拉角来表示2SPS+RRR机构中坐标系oxyz相对于坐标系OXYZ的旋转, 即动坐标系oxyz先与静坐标系OXYZ重合, 然后绕静平台坐标系X轴旋转α角, 接着绕新坐标系的z′轴旋转β, 最后绕新坐标系的y″轴旋转γ角得到.则描述机构姿态的旋转矩阵可表示为

(41)

由yl=0, 可得β=0.从而旋转变换矩阵(41)可以简化为

(42)

由式(31)和(42)两种变换矩阵可得:

(43)

把式(43)代入式(40)中可得:

(44)

由式(44)可以看出, 此机构动平台位置Xo、Yo、Zo相互耦合.Xo、Yo、Zo是关于其广义坐标α、γ、Zo的函数.动平台中心点o相对于静平台中心点O的线速度可表示为

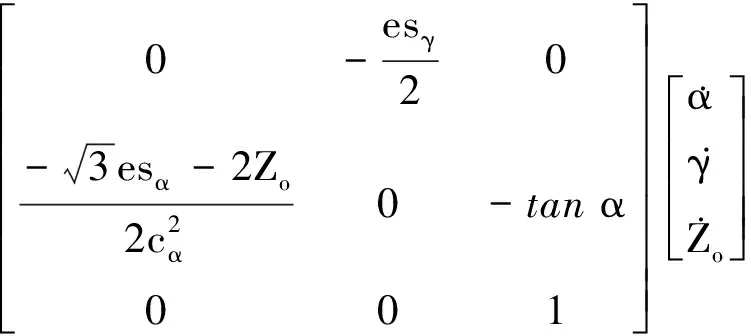
(45)

此机构的动平台m相对于静平台B的角速度可表示为欧拉角速度的叠加, 如式(46)所示.

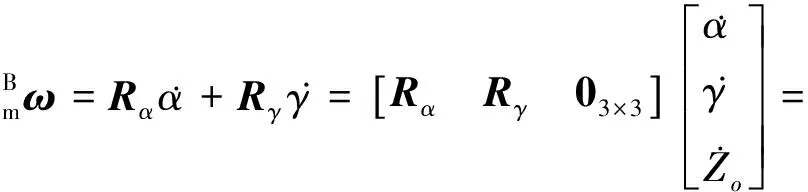
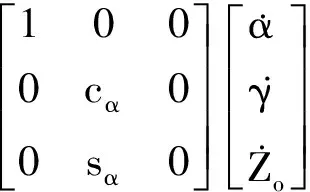
(46)

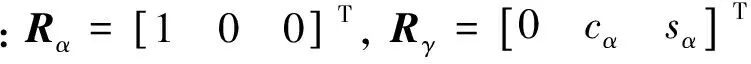
由式(45)和(46)可得:

(47)

式(47)为上端并联机构模块的末端6维速度与广义坐标速度间的映射关系,Jo为机构的速度解耦矩阵.

2.3 混联机构整体雅可比矩阵的建立

对于混联机构中的旋转变换矩阵, 定义下端并联机构的静平台为B1, 动平台为m1, 上端并联机构的静平台为B2, 动平台为m2, 则它们之间的变换关系可以表示为

(48)

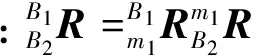
由于上端并联机构的静平台坐标系相对于下端并联机构动平台的坐标系绕着Z轴旋转了-30°, 则:

(49)

机构末端平台中心o2在基坐标系B1中可表示为

(50)

式(50)对时间求导可以得到:

(51)

机构末端平台m2相对于基坐标系B1的角速度[15]可表示为

(52)

由式(51)和(52)可知, 混联机构末端平台m2相对于基坐标系B1的速度为

(53)

在此定义一种运算, 设p=[pxpypz]T, 则G(p)满足

(54)

则JR1和JR2的表达式可以写为

(55)

由2.1和2.2节分别求解的下端并联模块和上端并联模块的雅可比矩阵可得:

(56)

为了区分2个并联机构模块, 位于下端的并联机构2SPS+RPR称为机构1, 位于上端的并联机构2SPS+RRR称为机构2, 故对输入参数加下标加以区分.

将式(56)代入式(53)中, 可得

(57)

(58)

式中:JF为整个混联机构的正向雅可比矩阵.

3 六自由度混联机构奇异性分析

机构的奇异位形是机构的固有属性, 是机构在运动过程中的某些特殊的位置, 其对机构的各方面, 如力传递性能、关节控制等, 都有着巨大的影响.串联机构的奇异位形是指机构末端失去自由度, 而并联机构的奇异位形是指动平台得到了局部的瞬时自由度, 所以当机构处于奇异位形, 会造成机构自由度变化, 引起机构瞬时可控制关节数目减少, 降低了机构的可操作性, 机构失去稳定性[20], 导致机构的操作速度会趋于无穷大, 对机构造成不良的冲击, 机构可能因此被破坏.机构的自由度变化导致在实际使用过程中可操作度变化.机构处于奇异位形时, 机构的雅克比矩阵行列式为零[21].因此, 在设计和应用混联机构时, 需对其奇异位形进行分析, 并避开各奇异位形点.

运用代数法分析混联机构的奇异位形, 即通过判别混联机构的雅可比矩阵是否满秩来判定机构是否位于奇异位形.通过求解机构的速度雅可比矩阵, 得到一个6×6的方阵.然后求解此雅可比矩阵的行列式, 再令雅可比矩阵的行列式值为零, 从而求得此非线性方程的根, 得到机构位于奇异位形时的位置与姿态参数.

代数法易于理解且使用广泛, 但是混联机构行列式等于零所对应的非线性方程非常复杂, 求解难度很大.由2.3节求得了双并联型混联机构的正向整体雅可比矩阵的符号解, 由于机构的参数过多, 故对机构的结构参数用表1中的数据代入, 这样整个行列式就只剩6个参数, 即关于下端并联机构模块的r0、α1、β1和上端并联机构模块的α2、γ2、Z0.

表1 混联机构结构参数

给定双并联型混联机构下端3个参数, 求解混联机构末端在三维空间中的奇异轨迹的分布, 然后通过MAPLE软件绘制出此条件下机构的奇异轨迹分布图.混联机构末端在不同的下端并联机构模块的位置姿态参数下得到的奇异轨迹分布情况如图4所示.

为了得到更为一般性的情况下双并联型混联机构的奇异轨迹, 任意给定整个机构的3个参数, 从而求解混联机构末端在三维空间中的奇异轨迹的分布.给定机构的结构参数如表1所示, 混联机构末端在不同的条件下, 在三维空间中的奇异轨迹的分布如图5所示.

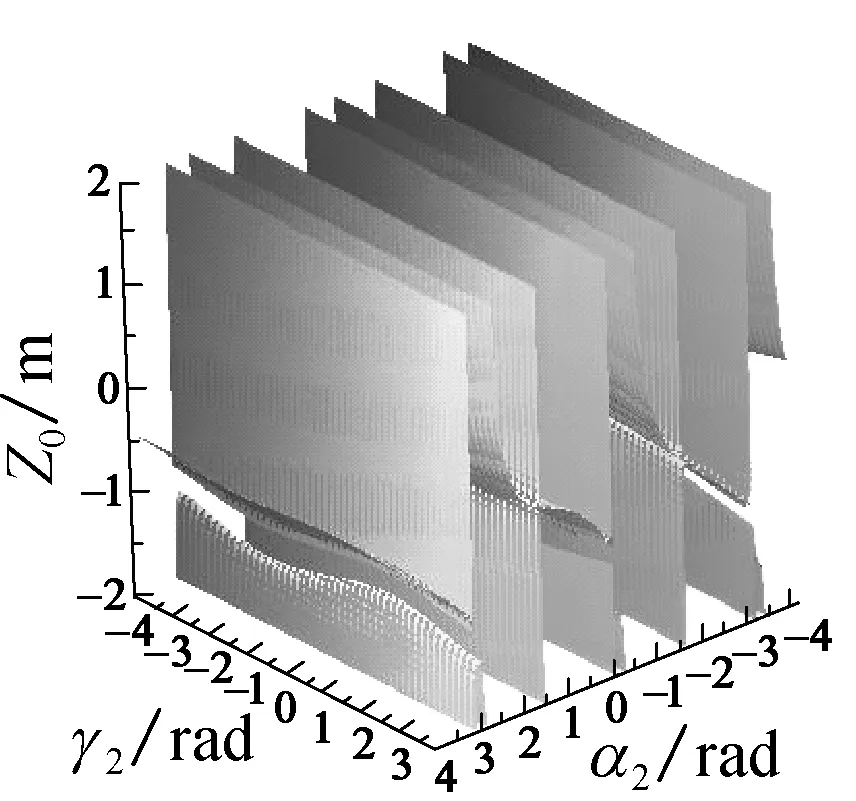
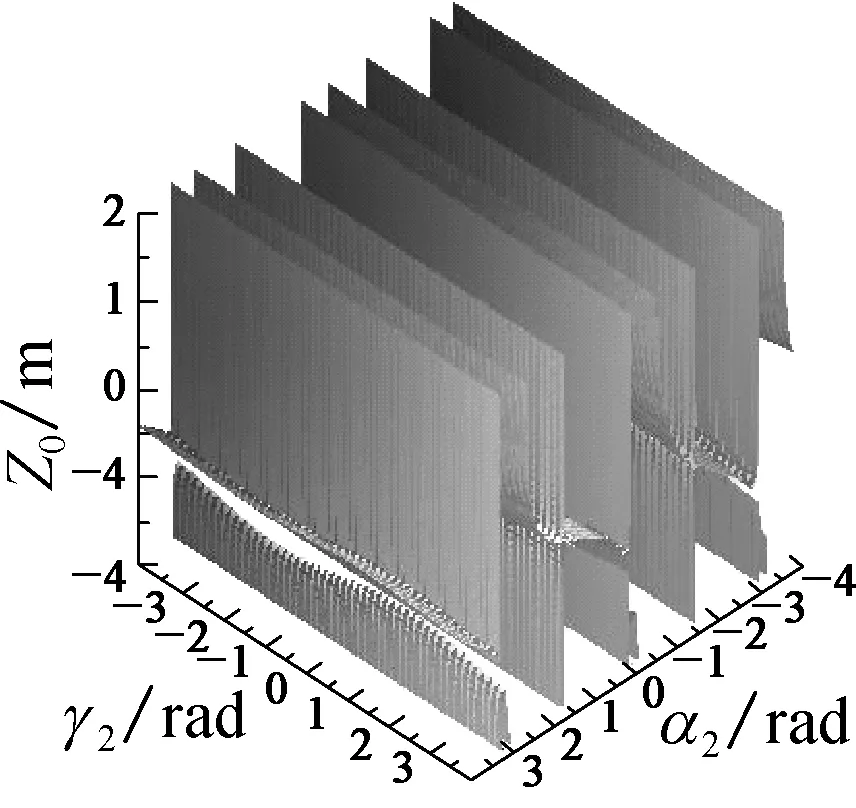
图4 混联机构处于不同的下端并联机构模块的位置姿态参数下奇异轨迹

Fig.4 Singularity trajectory of the hybrid mechanism in the different position and orientation parameters of the lower parallel modules

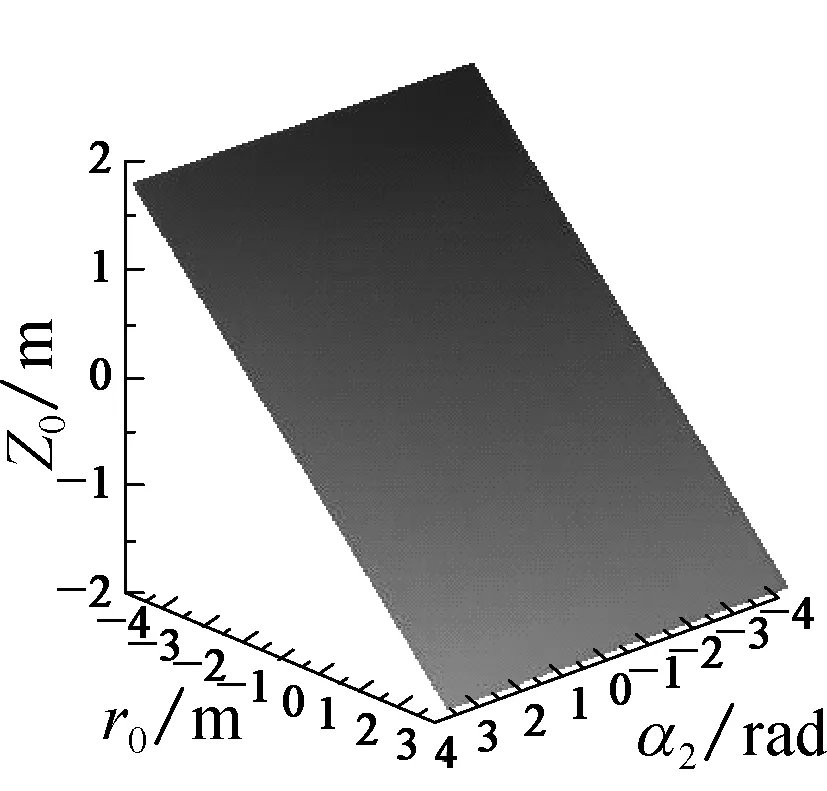
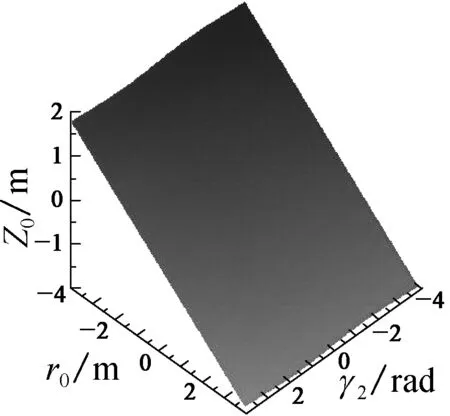
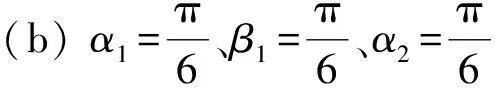
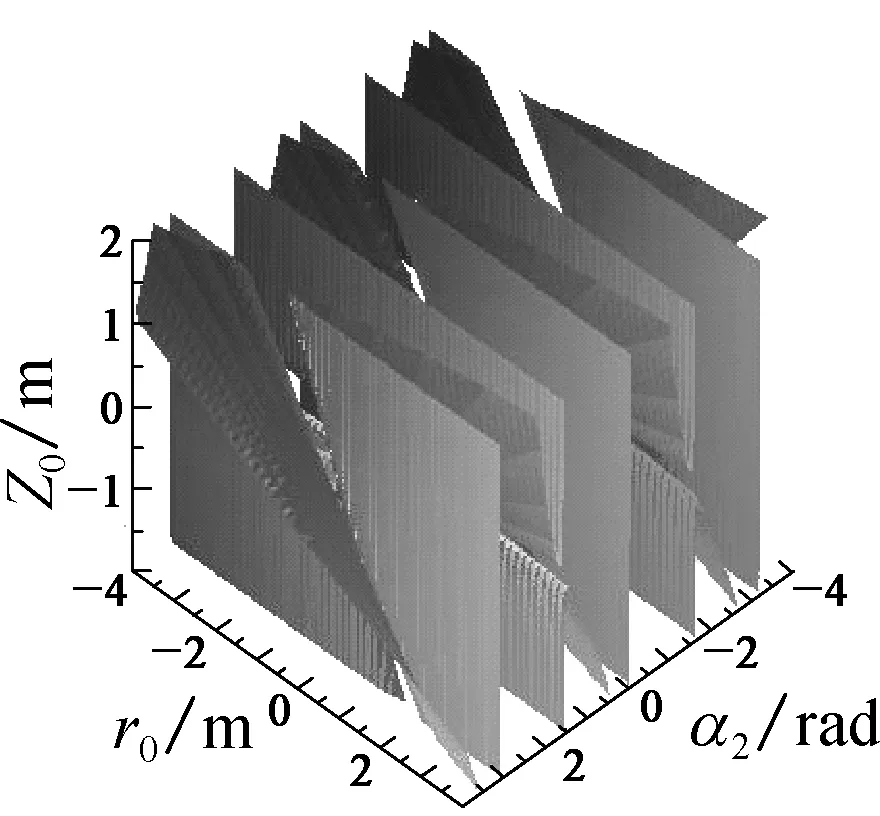
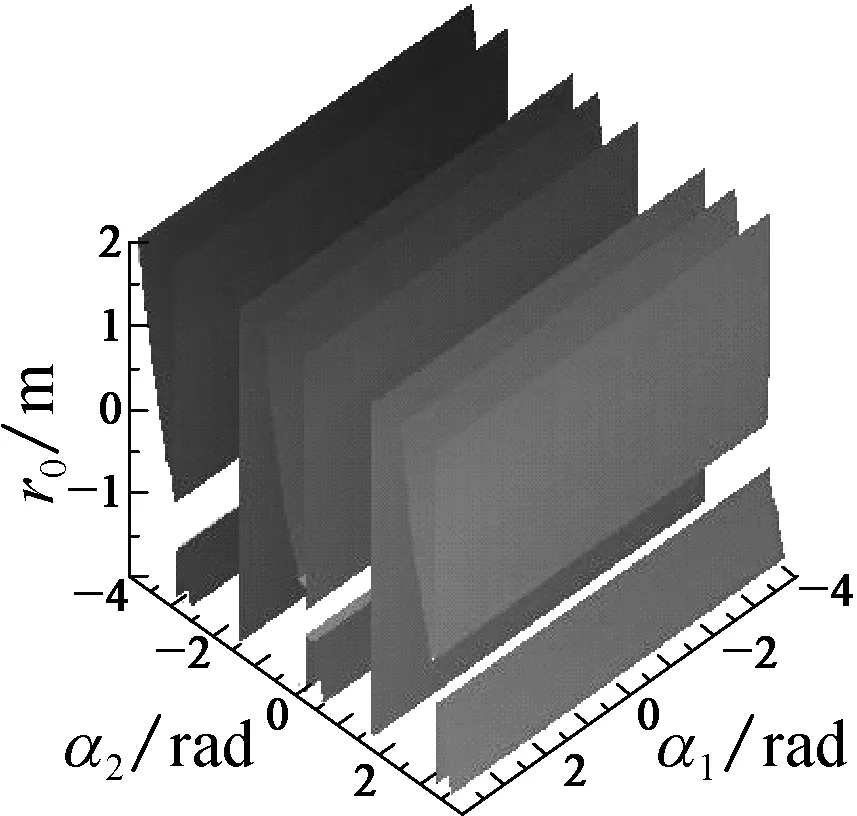
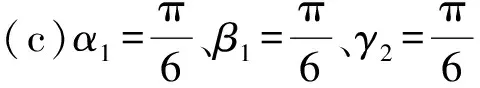
图5 混联机构处于不同条件下的奇异轨迹

Fig.5 Singularity trajectory of the hybrid mechanism in the different condition

观察图4和5的奇异轨迹可以发现, 机构不同模块给定不同的参数时, 另3个参数会有不同的奇异位形轨迹.由图4可知: 当给定下端机构的参数, 下端姿态相同,r0越大, 上端3个参数的奇异轨迹的缺口越往上；当r0相同,α1、β1值越大时, 缺口的变化越平缓.图5给出了整个混联机构任意的3个参数时的奇异轨迹, 末端给定不同参数时整个混联机构的奇异轨迹非常复杂而且多变.同时在混联机构的位形空间中, 奇异点的出现是连续的一个曲面或者高维曲面.通过对双并联型混联机构的奇异位形分析, 可以得到机构在不同状态下的奇异位形曲面的分布, 对更加深入地了解此机构的奇异位形有着重要的理论意义.

4 结 语

(1) 本文介绍了双并联型六自由度混联机构的结构形式, 根据六自由度混联机构的结构特点及几何约束, 分别建立了上端、下端2个并联机构模块的速度传递雅可比矩阵, 然后通过上下并联模块的运动关系, 将2个独立并联机构模块的速度耦合和约束关系联系起来, 分析了整个混联机构的速度传递关系, 从而建立了整个混联机构整体正向雅可比矩阵.

(2) 通过判定整体雅可比矩阵是否满秩来判断机构是否奇异, 分析机构的奇异位形, 通过令雅可比矩阵行列式为零得到了一个非线性方程, 给定机构的结构参数及其中不同条件下的3个参数, 由MAPLE软件得到其符号解, 并绘制出混联机构的奇异轨迹图.

[1] YAN C Y, GAO F, ZHANG Y. Kinematic modeling of a serial-parallel forging manipulator with application to heavy-duty manipulations [J]. Mechanics Based Design of Structures & Machines, 2010, 38(1): 105-129.

[2] LIU D, WANG T, TANG C, et al. A hybrid robot system for CT-guided surgery[J]. Robotica, 2010, 28(2): 253-258.

[3] ALTUZARRA O, SALGADO O, PETUYA V, et al. Computational kinematics for robotic manipulators: Jacobian problems[J]. Engineering Computations, 1984, 25(25): 4-27.

[4] HUNT K H. Structural kinematics of in-parallel-actuated robot-arms[J]. Journal of Mechanical Design, 1983, 105(4): 705-712.

[5] FICHTER E F. A stewart-platform based manipulator: General theory and practical construction[J]. International Journal of Robotics Research, 1986, 5(2): 157-182.

[6] MERLET J P. Parallel manipulators part 2 : Theory singular configurations and grassmann geometry[J]. HAL-INRIA,1988，(8): 194-212.

[7] GOSSELIN C, ANGELES J. Singularity analysis of closed-loop kinematic chains[J]. IEEE Transactions on Robotics & Automation, 1990, 6(3): 281-290.

[8] GREGORIO R D. Forward problem singularities of manipulators which become PS2RS or 2PSRS structures when the actuators are locked[J]. Journal of Mechanical Design, 2004, 126(4): 640-645.

[9] 黄真, 曲义远. 空间并联机器人机构的特殊位形分析[J]. 燕山大学学报, 1989, 13(2): 1-6.

[10] 李艳文. 几类空间并联机器人的奇异研究[D]. 秦皇岛: 燕山大学机械工程学院, 2005.

[11] 李秦川, 孙晓东, 陈巧红, 等. 2-PRS-PRRU并联机构运动学与奇异分析[J]. 机械工程学报, 2011, 47(3): 21-27.

[12] 曹毅, 黄真, 李艳文. 3/6-SPS型Stewart并联机构奇异轨迹的性质识别[J]. 中国机械工程, 2006, 17(4): 391-396.

[13] LI B, CAO Y, ZHANG Q, et al. Position-singularity analysis of a special class of the Stewart parallel mechanisms with two dissimilar semi-symmetrical hexagons[J]. Robotica, 2013, 31(1): 123-136.

[14] 李永刚, 宋轶民, 冯志友, 等. 4自由度非全对称并联机构的完整雅可比矩阵[J]. 机械工程学报, 2007, 43(6): 37-40.

[15] 胡波, 宋春晓, 张庆玲, 等. 2(2-UPR+SPR)串并联机构雅可比矩阵的建立[J]. 中国机械工程, 2015(7): 853-858.

[16] GAO Z, ZHANG D. Performance analysis, mapping and multiobjective optimization of a hybrid robotic machine tool[J]. IEEE Transactions on Industrial Electronics, 2015, 62(1): 423-433.

[17] 黄真, 刘婧芳, 曾达幸. 基于约束螺旋理论的机构自由度分析的普遍方法[J]. 中国科学, 2009, 39(1): 84-93.

[18] 杨文玉, 孟富明. 锻造操作机顺应性能评价与优化方法[J]. 机械工程学报, 2010, 46(23): 121-127.

[19] 石岩. 基于移/转动Jacobian矩阵的少自由度并联机构性质研究[D].秦皇岛: 燕山大学机械工程学院, 2010.

[20] MASOULEH M T, GOSSELIN C. Singularity analysis of 5-R P UR parallel mechanisms (3T2R)[J]. International Journal of Advanced Manufacturing Technology, 2011, 57(57): 1107-1121.

[21] CHOI H B, RYU J. Singularity analysis of a four degree-of-freedom parallel manipulator based on an expanded 6×6 Jacobian matrix[J]. Mechanism & Machine Theory, 2012, 57(57): 51-61.

(责任编辑: 徐惠华)

Solution of Jacobian Matrix and Analysis on Singularity Configuration of a 6-DoF Hybrid Mechanism

ZHOUHui1, 3,DINGRui1, 3,CAOHaofeng1, 3,CAOYi1, 2, 3

(1. School of Mechanical Engineering, Jiangnan University, Wuxi 214122, China;2. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University, Shanghai 200240, China; 3. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, Wuxi 214122, China)

A hybrid mechanism which is in serial connection with two 3-DoF parallel mechanisms with different configuration is presented. The integrated Jacobian matrix is combined by the upper and lower parallel modules, through the motion relationship of the two parallel modules. Jacobian matrix is the basis of analyzing the singularity of mechanism. By making the integral Jacobian matrix determinant of the mechanism equal to zero, the nonlinear equation about the singularity of the mechanism is obtained, which is used to study the singularity configuration of the hybrid mechanism, meanwhile the trajectory of singularity is drawn by MAPLE. The Jacobian matrix of the hybrid mechanism composed of two different parallel modules is established, which has a certain theoretical significance.

hybrid mechanism; Jacobian matrix; parallel module; singularity configuration

1671-0444 (2017)03-0416-09

2016-05-10

国家自然科学基金资助项目(50905075)；机械系统与振动国家重点实验室开放课题资助项目(MSV201407)；江苏省食品先进制造装备技术重点实验室开放课题资助项目(FM-201402)

周 辉(1973—)，女，河北秦皇岛人，讲师，硕士，研究方向为混联机器人机构学理论及机器人技术.E-mail：roboticscenter@qq.com 曹 毅(联系人)，男，教授，E-mail：caoyi@jiangnan.edu.cn

TH 112

A