微滴撞击织物表面沉积过程建模研究

肖 渊， 申 松， 张津瑞， 刘金玲， 吴 姗， 杨鹏程

(西安工程大学 机电工程学院 陕西 西安 710048)

微滴撞击织物表面沉积过程建模研究

肖 渊， 申 松， 张津瑞， 刘金玲， 吴 姗， 杨鹏程

(西安工程大学 机电工程学院 陕西 西安 710048)

为明确微滴与织物表面的碰触、铺展及渗透机理，基于最小势能原理，得到了纱线的中心线模型，通过研究纤维在纱线截面内的分布规律以及纤维体积分数的计算方法，建立了织物单胞的二维几何模型.在上述建立的织物模型基础上，依据流体体积(volume of fluid， VOF)两相流模型，建立了单颗微滴撞击织物表面后沉积变形的模型.利用所建立的模型，进行微滴与织物基底的碰撞及渗透过程仿真研究，并将模拟过程与试验进行对比. 结果表明，所建模型可实现对微滴在织物基底的碰撞及渗透过程的模拟，整个过程与试验结果吻合较好.该研究方法与结果为后续不同工艺参数下微滴在织物表面沉积过程的研究奠定了基础.

织物； 建模； 纤维分布； 微滴； 沉积； 碰撞； 渗透

智能纺织品是一种将纺织品与电子信息技术高度融合的新型纺织品.它是将传感器、执行器、数据处理、通信、电源等单元集成到纺织品中，使之具备信息采集、信息识别、检测反馈、积累与响应等功能，可以实现自诊断、自修复和自适应等能力，在军事、航空、航天、生物医学、体育休闲、娱乐、医疗保健等领域有着重要的应用前景[1].如何将电子元件与纺织品有效集成，使其不仅满足织物功能需求，还能保证纺织品的耐水洗、耐磨损及穿着舒适是智能纺织品研究的焦点.将微滴按需喷射3D打印技术与化学沉积相结合，再将金属盐和还原剂溶液精确打印在织物表面的指定位置，从而在室温下还原出金属微粒，可以实现微细导电线路的直接打印成形[2].但在织物表面微滴喷射打印沉积过程中，因织物表面与一般固体基板不同，具有高粗糙度和多孔等复杂特征.试验手段只能观测微滴在织物表面的形态变化，无法掌握内部压力场变化及微滴在织物截面内的渗透过程.基于此，本文通过建立微滴与织物基板碰撞及渗透过程的理论模型，对微滴与织物基板碰撞、渗透过程进行研究，为后续打印高质量微细导电线路奠定理论基础.

国内外学者对微滴在不同基板的沉积过程进行了较为深入的研究.文献[3-5]采用VOF(volume of fluid)法实现了金属熔滴在固体基板沉积和凝固过程的模拟. Bussmann等[6]建立了液滴与固壁碰撞的三维模型，采用有限差分法在固定网格上求解动量和能量守恒方程，以VOF方法跟踪液滴在自由表面的流动.李素丽等[7]利用建立的VOF模型对整个熔滴沉积流固耦合过程进行数值模拟，分析了熔滴滴落及在基板壁面上的铺展状态.Verleye等[8]针对无皱褶织物和平纹织物建立了细观几何模型，模拟了树脂在织物单胞内的流动.Chen等[9]采用FLOTRAN CFD软件对织物模型进行了简化，模拟了树脂在平纹织物纱线区域内的流动.戴福洪等[10]建立了平纹织物的几何结构模型，采用均匀化方法预测了树脂在该模型中的渗透率.上述研究主要集中在微滴与固体基板碰撞以及微滴在织物内纱线间渗透两方面.但是针对微滴在纱线内部纤维间渗透过程的动态仿真及其试验验证的研究较少.本文以平纹织物为研究对象，在充分考虑纱线内部可渗透性基础上，建立织物的二维几何模型；采用VOF法建立单颗液滴在织物表面的沉积碰撞、渗透模型，利用所建立的模型对液滴在织物基板的沉积变形过程进行研究，明确微滴在织物表面的沉积过程，为后续织物表面导电线路的精确沉积奠定基础.

1 纱线模型的建立

确定纱线模型是织物建模的基础，在其建模过程中，通常依据纱线截面形态和中心线的屈曲形态构成纱线的包络曲面，来表示纱线的整体形状. 纱线模型的建立包括纱线中心线模型、纱线截面模型、纤维分布模型以及纤维体积分数的计算方法.

1.1 纱线中心线模型

常见的纱线中心线模型有正弦曲线、贝塞尔曲线、B样条曲线、自然三次样条曲线等.本文基于最小势能原理求解得到纱线中心线的几何表达式，从而得到更接近实际的纱线中心线模型.平纹织物纱线编织结构如图1所示，其中曲线z(x)表示纱线的中心线路径，T表示织物厚度，S表示相邻纱线中心线的间隔，h表示纱线厚度，w表示纱线宽度，h0表示纱线卷曲高度.

图1 平纹织物编织结构图Fig.1 Plain fabric weave structure

在弯曲间隔S内单根纱线弯曲势能为

(1)

式中：W为弯曲势能；B为纱线弯曲刚度；括号内式子表示纱线中心线曲率.对单根卷曲纱线利用最小势能原理，可得纱线中心线路径的表达式z(x)的近似结果为

(2)

1.2 纱线截面模型

纱线的横截面有圆形、椭圆形、跑道形、透镜形等.由于经纬纱在交叉处相互受力而形成类似于透镜形截面.该截面是由两个半径分别为r1和r2的圆交叉而成.由于经纬纱在交叉时有力的作用产生，纱线截面的上部分会在力的作用下向下压而发生变形，使其产生变形距离d，截面其他部分的参数如半径r1、r1以及圆心O1、O2纵坐标y1、y2可由纱线宽度w、高度h以及变形距离d根据式(3)～(6)计算而来.

(3)

(4)

(5)

(6)

透镜形纱线截面的参数方程如下：

(7)

(8)

(9)

两种典型的透镜形纱线截面如图2所示，如果纱线变形距离d=0，则两个圆的半径和偏移量相等，这是理想的状态下，两段圆弧成对称形分布(图2(a)).实际上，纱线在编织过程中不可避免地会产生扭曲变形，图2(b)更接近真实的织物纱线截面形状.

图2 透镜形纱线截面Fig.2 Lenticular cross-section of the yarn

1.3 纤维分布模型

单根纱线是由多根纤维以一定的捻度扭曲而成，因纤维在纱线内的分布受多种因素影响，为简化计算做如下假设[11-12]：

(1) 纤维以半径相等的圆分布于纱线截面内；

(2) 纤维在纱线截面内按层分布；

(3) 同一层纤维的圆心分布于一条曲线上.

因此，确定纤维圆心的分布曲线，使纤维以一定的间隙分布于纱线截面上是纤维建模的关键. 为获得纤维圆心的分布曲线，需先确定曲线所在的截面C(t，μ).引入两个横截面A(t)和B(t)(整个纱线截面)，其关系如下所示：

C(t，μ)=A(t)+(B(t)-A(t))μ

0≤t≤1 0≤μ≤1

(10)

式中：μ在截面A(t)和B(t)从0到1成线性变化，从而使纤维在层与层之间平稳过渡.图3为透镜形纱线截面内纤维圆心分布的曲线图.

图3 透镜形截面内纤维圆心分布曲线图Fig.3 Distribution of circle of fiber center in the lenticular cross-section

为了使纤维层与层之间具有更好的连续性，采用一个三次方程式来表示μ与x之间的关系.

当x=0时

μ=0

(11)

当x=L时，L为纤维层与层之间的距离，则

μ=1

(12)

因此，可得如下方程：

(13)

1.4 纤维体积分数

确定纤维的多少及纤维的间距，对后续研究微滴在织物内渗透性至关重要.图4为纱线截面内纤维体积分数示意图，其中，AF为纱线截面内纤维的面积，AY为纱线截面面积.

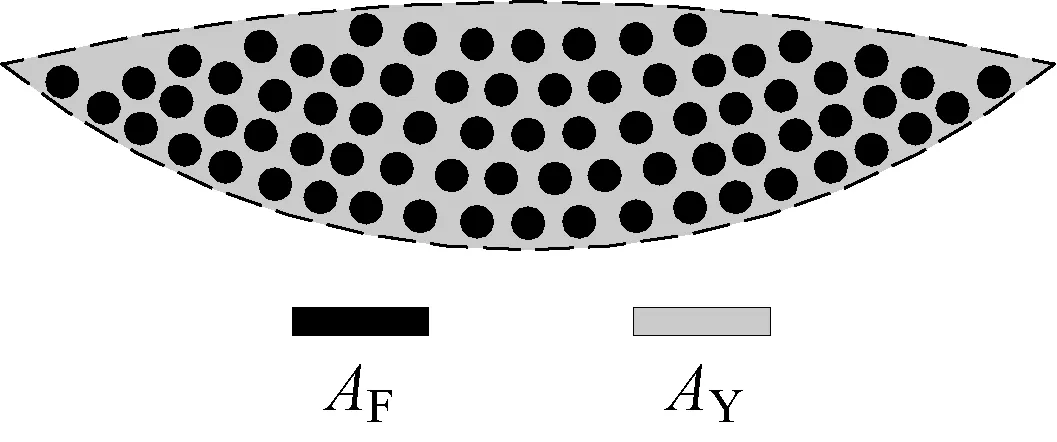
图4 纱线截面内纤维体积分数示意图Fig.4 Fiber volume fraction in the yarn cross-section

建模时，通过试验测量纱线或织物的质量m，计算出纱线或织物总的纤维体积VF，假设所有纤维的密度ρ相等，则：

(14)

利用式(15)可计算出纱线中纤维的体积分数φF

(15)

式中：VY为纱线体积.

此种方法得到的是整个纱线或织物的纤维体积分数，适于纱线横截面沿着纱线方向不发生显著变化的情况. 但是对于大多数纱线截面发生变化的情况，一个截面内纤维的面积AF与纱线截面面积AY的比例更能反映纤维体积分数. 假设纤维是不可压缩的且纤维面积在纱线截面内沿着纱线长度方向不发生变化. 因此纤维面积分数ωF为：

(16)

给定纱线的线密度ζ和组成纤维的密度ρ,则：

(17)

2 平纹织物模型的建立

由于织物结构的复杂性，处于不同编织结构和受力状态下的织物几何结构差距较大，本节利用文献[13]给出的涤纶平纹织物建立几何模型，其实物照片和详细参数设置如图5和表1所示.

图5 平纹织物实物图[13]Fig.5 Plain fabric

表1 Chomarat 150 TB织物参数[13]

利用表1中参数，建立织物的二维几何模型如图6(a)所示，图6(b)为实际织物纱线截面SEM图[13].

(a) 所建立的织物几何模型

(b) 纱线截面SEM图

图6 织物几何模型

Fig.6 Fabric geometry model

由图6可看出一个单胞由两根经纱和两根纬纱组成.经纱内纤维分三层分布，依次有12根、9根、3根共24根纤维组成.而垂直于经纱方向的纬纱由三层纤维组成.由纱线截面内纤维分布放大图可以明显地看出，纤维之间以及纤维层与层之间都有一定的间隙.通过对比实际织物的SEM图，可以看出建立的几何模型与真实织物较一致.

3 织物表面微滴沉积过程建模

为了研究微滴在织物表面的沉积过程，本节采用Fluent 软件中的VOF两相流模型建立控制方程，通过求解单独动量方程和处理穿过区域的每一流体的体积比来模拟两种以上不相容流体.该过程涉及液滴和空气两种流体，假设二者间无热传质、非压缩流体，且黏性系数、表面张力系数等都是常数.

3.1 流动控制方程组

根据VOF方法，通过求解连续性方程

(18)

式中：v为速度矢量.

用体积分数γ来追踪气液交界面.对液相流体，γ=0表示单元是空的，γ=1表示单元充满，0<γ<1表示单元为气液两相界面.VOF模型中，动量方程为

(19)

ρ=γ1ρ1+(1-γ1)ρ0

(20)

μ=γ1μ1+(1-γ1)μ0

(21)

式中:F为表面张力源项；p为压力；g为重力矢量；ρ为计算单元内密度；μ为计算单元内动力黏度；下标0表示气相，1表示液相.

表面张力源项采用Brackbill提出的连续表面力(CSF)模型来求解. 能量方程为

(22)

式中：cp为计算单元内比热容；T为计算单元内温度；λ为计算单元内导热系数.

对于流体在纱线内部的流动，将纱线看作多孔介质，采用Brinkman方程描述流体流动，如式(23)所示.

(23)

式中：Kyarn为纱线的渗透率张量.

3.2 计算区域的确定

由于各部分流体在沉积过程中始终沿轴向对称分布，为减少计算时间，只对区域的1/2进行求解并扩展至整个区域. 本文采用二维模拟，计算区域为738 μm×600 μm，包括流体区域(A区液滴和B区空气)和多孔区域(C区织物)，A和B区采用四边形均匀网格划分，C区采用非结构化网格划分，计算区域网格总数为17 146.计算区域和边界条件如图7所示，设边界处的压强为1.01×105Pa，液滴与壁面间采用无滑移边界条件.液滴表面为研究的自由表面，液滴周围为大气环境，求解时需考虑重力的影响，且重力加速度方向与液滴下落方向一致.

图7 计算区域网格划分及边界条件Fig.7 Grid of calculation area and boundary conditions

3.3 定解条件设置

由于金属盐和还原剂溶液均为水基溶液，其打印沉积过程与水相似，故本文以水微滴为研究对象，其物性参数如表2所示.

表2 水微滴物性参数

采用有限体积法对控制方程进行离散，压力速度的耦合采用PISO算法，压力求解采用PRESTO！方法，连续方程和动量方程采用二阶隐式格式求解，对时间一阶离散. 计算单元液相体积分数采用CICSAM方法离散求解，控制方程采用QUICK格式进行离散以减少假扩散提高精度，时间步长为Δt=5×10-7s， Δt内迭代次数为20，残差小于10-3，满足迭代收敛要求.

4 模拟结果及试验验证

微滴在织物表面沉积过程主要为微滴在织物表面的碰撞以及在织物内的渗透过程. 液体能不能润湿表面进而发生铺展取决于铺展系数SL/SG

SL/SG=σSG-σSL-σL

(24)

式中：σSG，σSL，σL为固-气界面、固-液界面、液-气界面的表面能.

当SL/SG>0时，液滴会完全润湿基质并且铺展为一层薄膜. 当微滴沉积在织物表面与其碰撞后首先主要沿径向铺展在织物表面，只有很少一部分液体会渗透到织物内部(本文模拟忽略此部分液体)，达到一个相对稳定的状态后，此后微滴继续渗透到织物内部[14-15].为了对沉积过程进行更深入细致的研究，把微滴在织物表面的沉积分为碰撞和渗透两个过程分别进行研究[16].

4.1 碰撞过程

微滴与织物表面的碰撞过程与在普通固体基板表面的碰撞过程相似[3]，多孔区域的边界条件采用Wall.设定微滴与基板的接触角为98°，织物孔隙率为15.8%，渗透率为480.7 D.碰撞过程试验采用笔者课题组自主开发的气压驱动式微滴喷射系统[2]，以机织平纹布为基板，通过调节控制参数实现微滴按需喷射，利用奥林巴斯i-speeds高速图像摄影系统对微滴与织物表面碰撞过程及渗透过程进行采集，得到微滴碰撞各阶段形态变化模拟结果与试验照片如图8所示，其中，上图为试验照片，下图为模拟结果.

图8 微滴碰撞过程模拟结果与试验照片对比Fig.8 Comparison of simulation results and experimental pictures in the droplet impact process

通过图8可看出，微滴与织物表面碰撞过程中，模拟结果与试验观测到各个阶段微滴的形态均吻合较好. 微滴与织物表面的碰撞过程经历了运动、射流、回缩阶段、随后振荡沉积直到平衡. 其射流和铺展阶段在0.9 ms时间内完成，微滴铺展达到最大直径的时刻为0.9 ms，此时微滴为类饼状. 随后进入回缩阶段，当运动到2.5 ms时，微滴第一次达到最大程度回缩位置. 此后经历铺展-回缩往复循环，直至能量完全消耗，最终约在34.9 ms时达到平衡状态.

4.2 渗透过程

渗透过程多孔区域的边界条件采用Porous Jump. 图9为微滴渗透过程模拟结果与试验照片，其中，上图为试验照片，下图为模拟结果.

图9 微滴渗透过程模拟结果与试验照片对比Fig.9 Comparison of simulation results and experimental pictures in the droplet permeation process

由图9可以看出，微滴沉积到织物表面后，随着时间的延续其在织物表面的形态不断发生变化，停留于织物表面液体体积在不断减少，最终完全渗入织物中. 微滴在织物内部渗透初期，渗透速度非常快. 为分析微滴渗透速率加快的原因，提取微滴在24 ms时刻的压力云图如图10所示.

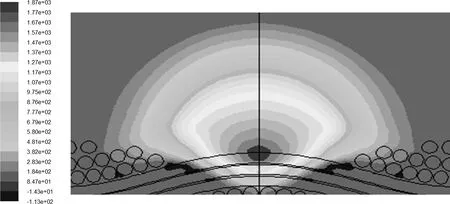
图10 24 ms时刻微滴压力云图Fig.10 Droplet pressure cloud diagram at 24 ms

由图10可看出，微滴内部压力分布不均，梯度较大，上部为低压区，微滴与织物接触区域为高压区，从上向下压力越来越大. 这是由于微滴渗入织物内会产生毛细力的作用，导致毛细压差的产生，从而使液体自发地在毛细孔隙中流动，开始阶段毛细压差大，织物中的孔隙顺畅，液体渗入快，孔隙不断地被液体所填充，出现快速芯吸现象，这与文献[17]中的描述相吻合. 随着压差的减小，微滴的渗透速率逐渐减小，使得渗透过程减缓，直至液体完全渗入织物内部，达到稳定状态.

由图8和9的模拟结果与试验照片对比可知，微滴与织物表面碰撞、铺展及渗透直至稳定状态的整个过程中，模拟结果与试验观测到各个阶段微滴的形态均吻合较好，且从模拟的结果可以非常清楚的看到液滴在织物内部的渗透过程，表明模拟结果符合实际情况，证明了本文所提出的建模方法可行，为后续液滴在织物表面沉积过程的进一步研究奠定了基础.

5 结 论

(1) 依据最小势能原理建立了织物单胞的几何模型，将纱线的受力与其几何形态联系起来，得到与实际织物结构相吻合的模型；

(2) 微滴在织物内部渗透初期，由于毛细压差的作用使其渗透速率加快，出现快速芯吸现象；

(3) 微滴与织物表面碰撞、渗透过程的模拟结果与试验结果吻合良好，表明提出的建模方法是合理可行的，为研究微滴的精确沉积奠定了基础.

[1] KIEKENS P， JAYARAMAN S. Intelligent textiles and clothing for ballistic and NBC protection： Technology at the cutting edge [M]. Croatia Springer， 2012：119-136.

[2] 肖渊，黄亚超，蒋龙，等.喷射打印和化学沉积成形微细电路中微滴可控喷射研究[J].中国机械工程，2015，26(13)：1806-1810.

[3] 曾祥辉，齐乐华，蒋小珊，等.金属熔滴与基板碰撞变形的数值模拟[J].哈尔滨工业大学学报，2011，43(3)：70-74.

[4] LI H J， WANG P Y， QI L H， et al. 3D numerical simulation of successive deposition of uniform molten Al droplets on a moving substrate and experimental validation[J]. Computational Materials Science， 2012， 65(4)： 291-301.

[5] LI H P， LI H J， QI L H， et al. Simulation on deposition and solidification processes of 7075 Al alloy droplets in 3D printing technology[J]. Transactions of Nonferrous Metals Society of China， 2014， 24(6)： 1836-1843.

[6] BUSSMANN M， CHANDRA S， MOSTAGHIMI J. Modeling the splashing of a droplet impacting a solid surface[J]. Phys Fluids， 2000， 12(12)：3121-3132.

[7] 李素丽，刘伟，贾宝勤.金属沉积成形流固耦合工艺参数[J].江苏大学学报，2015，36(5)：588-592.

[8] VERLEYE B， LOMOV S V， LONG A. Permeability prediction for themeso-macro coupling in the simulation of the impregnation stage of resin transfer moulding[J]. Composites： Part A， 2010， 41(1)： 29-35.

[9] CHEN Z R， Ye L， LU M. Permeability predictions for woven fabric preforms[J]. Journal of Composite Materials， 2010， 44(13)：1569-1586.

[10] 戴福洪，张博明，杜善义.用均匀化方法预报平纹织物的渗透率[J].复合材料学报，2009，26(2)：90-93.

[11] 于伟东，王锦成.纤维分布和混纺比对毛涤混纺纱毛型感的影响[J].东华大学学报(自然科学版)，2001，27(1)：24-28.

[12] 邰文峰，徐鑫华，宫菡菡.混纺纱线中纤维的分布测试探讨[J].现代纺织技术，2010，26(1)：42-45.

[13] MARTIN S. Geometric and mechanical modelling of textiles[D]. Nottingham：The University of Nottingham， 2007.

[14] GOLPAYGAN A， HSU N， ASHGRIZ N. Numerical investigation of impact and penetration of a droplet onto a porous substrate[J]. Journal of Porous Media， 2008， 11(4)：323-341.

[15] EDIN B， Numerical simulations of flow due to drop impact on a porous substrate using a permeable wall model[C]//19h International Research/Expert Conference.2015:22-23.

[16] 刘晓娜.喷墨印刷在织物上的应用研究——薄织物上墨滴铺展与渗透理论模型[D].无锡：江南大学纺织学院，2011.

[17] 范菲，齐宏进.织物孔径特性与织物结构及芯吸性能的关系[J].纺织学报，2007，28(7)：38-41.

(责任编辑：杜 佳)

Research on the Deposition of Micro-droplet by Modeling Its Impacting Process on the Fabric Surface

XIAOYuan，SHENSong，ZHANGJingrui，LIUJinling，WUShan，YANGPengcheng

(College of Mechanical and Electrical Engineering，Xi’an Polytechnic University， Xi’an 710048， China)

To clarify the mechanism of droplets impacting the fabric surface and then their spreading and penetration process， a yarn centerline model is obtained based on the principle of minimum potential energy. A two-dimensional geometric model of the unit cell of the fabric is established by studying the distribution of the fibers in the yarn cross-section and the calculation method of the fiber volume fraction. Based on the fabric model built above， a two-phase flow model for a single droplet depositing and then deforming on the fabric surface is developed based on the volume of fluid (VOF) method. Using the established model， the process of the droplet/ fabric substrate collision and penetration have been simulated and investigated. Results from the simulation and experiment are compared. The results show that the model can realize the simulation of the colliding of droplets with fabric substrate and the penetration process. Result of the whole process is in good agreement with the experimental results. The method and results of the research can provide a foundation for the subsequent study on the influence of process parameters on the process of droplet deposition on the fabric surface.

fabric； modeling； fiber distribution； droplet； deposition; collision; penetration

1671-0444 (2017)03-0352-07

2016-09-02

国家自然科学基金资助项目(51475350)；西安工程大学学科建设经费资助

肖 渊(1975—)，男，陕西咸阳人，副教授，博士，研究方向为微制造系统与机电控制技术.Email: xiaoyuanjidian@xpu.edu.cn

TH 16

A