分布式部分校正子阵MIMO雷达角度估计算法

党婵娟， 张 炜， 胡羽行

(1. 大同大学 物理与电子科学学院， 山西 大同 037009； 2. 电子信息控制重点实验室， 四川 成都 610036；3. 北京理工大学 信息与电子学院， 北京 100081)

分布式部分校正子阵MIMO雷达角度估计算法

党婵娟1， 张 炜2， 胡羽行3

(1. 大同大学 物理与电子科学学院， 山西 大同 037009； 2. 电子信息控制重点实验室， 四川 成都 610036；3. 北京理工大学 信息与电子学院， 北京 100081)

针对子阵部分校正情况下的分布式子阵多输入多输出(MIMO)雷达角度估计问题， 提出了一种基于秩亏(RARE)方法的角度估计算法. 该算法通过利用分布式子阵MIMO雷达虚拟导向矢量的特殊结构， 在构造RARE角度搜索函数时将未知子阵间校正信息排除在外， 仅仅利用已知信息估计目标角度， 实现了整个阵列的有效利用， 进而提高了目标角度分辨率和定位精度. 为了评估所提算法的性能， 给出了对应的角度估计的克拉美罗界(CRB)， 仿真结果表明， 该算法在子阵信息未知或部分已知的条件下性能有效.

角度估计； 多输入多输出雷达； 子阵； 秩亏估计器

多输入多输出(MIMO)雷达利用多个发射天线发射相互正交的波形， 在接收端通过匹配滤波器提取出与发射波形相对应的回波信号， 从而形成具有更多自由度和更大阵列孔径的虚拟阵列. 相比于传统阵列雷达， MIMO雷达在目标角度估计方面有着明显的优势[1-3]. MIMO雷达的虚拟阵列与传统阵列具有相似的信号模型， 可以便于直接将阵列信号处理中的高分辨空间谱估计算法用于MIMO雷达的目标角度估计[4-5].

为了提高角度分辨率和定位精度， 常用少量的阵元来获得具有较长基线的稀疏阵列. 但是， 稀疏阵列会带来较高的旁瓣电平或栅瓣问题. 分布式子阵是由多个较小的子阵组成的一个相对大型的阵列， 兼具稀疏阵列的优势， 而且分布的小子阵非常方便运输和装备. 对于分布子阵式MIMO雷达， 虚拟阵元代替了子阵列之间缺失的阵元， 不仅消除了栅瓣， 还能造成阵列锥削的效果， 从而降低虚拟阵元方向图旁瓣电平. 但是， 子阵列之间的阵列间距、 幅相误差等信息可能获得不准确， 使得目标角度估计的性能下降[6].

本文主要研究分布子阵式MIMO雷达角度估计算法. 因为子阵列很小， 易于校正， 本文均假设每个子阵列是完全校正好的， 但是整个阵列没有校正好， 即子阵列之间存在校正误差， 如位置误差， 幅相误差等. 由于每个子阵列是校正好的， 因此可以利用每个子阵列进行角度估计， 但是整个阵列孔径并没有被有效利用， 而且自由度损失较大. 如果用整个阵列进行角度估计， 由于存在阵列误差， 造成传统空间谱估计算法的性能严重下降. 为了克服这些不利因素， 提出利用一种基于秩亏(RARE)算法来进行分布子阵式MIMO雷达的目标角度估计. 所提RARE算法利用分布子阵式阵列的结构特点， 将阵列的已知信息和未知参数分开， 从而利用各子阵列的已知信息估计目标角度， 忽略子阵列之间未知参数的影响.

1 信号模型

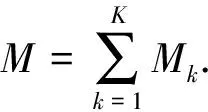
其中，

式中：vk(θ)是第k个子阵的导向矢量；h(θ,α)是K×1的误差矢量， 可以表示子阵间位置误差， 幅相误差等信息.

虚拟阵列的信号形式表示为

式中：b[n]=[b1[n],b2[n],…,bp[n]]T是目标反射系数矢量；A=[a(θ1)⊗a(θ1),…,a(θp)⊗a(θp)] 是虚拟阵列流形；n[n]是功率为σ2的白噪声. 假设所有目标回波信号及噪声之间是不相关的， 虚拟阵列的协方差矩阵可以表示为

Rx=E[x[n]x[n]H]=ASAH+σ2I=

2 算法原理

由多重信号分类(MUSIC)算法可知， 目标的角度估计(DOA)可以由空间谱的谱峰得到， 即[9-10]

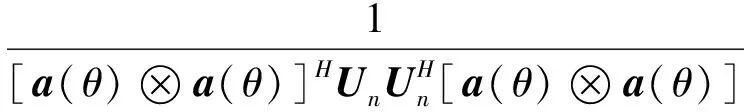
由于未知矢量参数α的存在， 必须用多维搜索来找到式(5)的峰值. 如果α中的未知参数不止一个时， 式(5)的峰值是很难找到的.

假设协方差矩阵Rx是已知的， 目标DOA可以通过以下方程获得

(6)

这里用RARE算法来克服多维搜索的困难[7]. 将式(1)代入式(6)， 可以得到

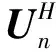
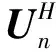
(h(θ,α)⊗h(θ,α))HZ(θ)(h(θ,α)⊗h(θ,α))=

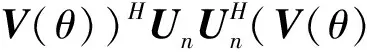
(8)

即M2-P≥K2时， 一般来说，Z(θ)是满秩的. 因此， 式(7)成立的条件是当且仅当Z(θ)是秩亏的， 即

也就是说， 当θ与真实的目标DOA重合时，Z(θ)才会出现秩亏. 在这种情况下，Z(θ)的最小特征值将取得最小值. 由此， 目标的DOA可以由空间谱函数

的峰值得到， 其中Mmin[·]表示获得矩阵最小特征值的操作算子.

由文献[7]的结论， 可以方便推导出分布子阵式MIMO雷达DOA估计的克拉美罗界(CRB). 首先定义一个(2KP-P)×1矢量

其中，

(12)

(13)

在上式中， 为了表达方便， 将h(θp,α)表示为

为了不产生模糊， 假设每个hp的第一个参数是固定的.

其中，

W=S(AHAS+σ2I)-1AHA.

由式(15)可以得到紧凑的CRB矩阵形式

CRB(η)=

其中⊙是Schur-Hadamard矩阵， 1是(2K-1)×1的全1矩阵. 这里， 矩阵D可以定义为

(19)

其中

式(21)中，ek是K×1的矢量， 其中第k个元素是1， 其他元素为0.

3 仿真结果

考虑一个由3个线阵组成的M=10阵元稀疏线阵MIMO雷达系统， 第一个子阵和第二个子阵相距10λ， 第一个子阵和第三个子阵相距16λ. 3个子阵列的指向是一样的. 假设3个同功率的不相干目标分别位于θ1=10°，θ2=20°和θ3=30°. 每个结果由100次仿真平均得到，L=100个快拍数据用于估计协方差矩阵.

3.1 子阵列之间距离未知时的角度估计性能分析

假设第一个子阵有4个阵元， 阵元间距为{0.35λ,0.6λ,0,43λ}； 第二个子阵有4个阵元， 阵元间距为{0.78λ,0.45λ,0.5λ}； 第三个子阵由两个相距0.5λ的阵元构成. 在这种情况下， 基于整个阵列的MUSIC算法不可用. 因此， 只将MUSIC算法用于第一个子阵. 图 1 给出了DOA估计的均方根误差(RMSE)随信噪比(SNR)变化的曲线. 可以看到， 所提RARE算法有着最好的估计性能.

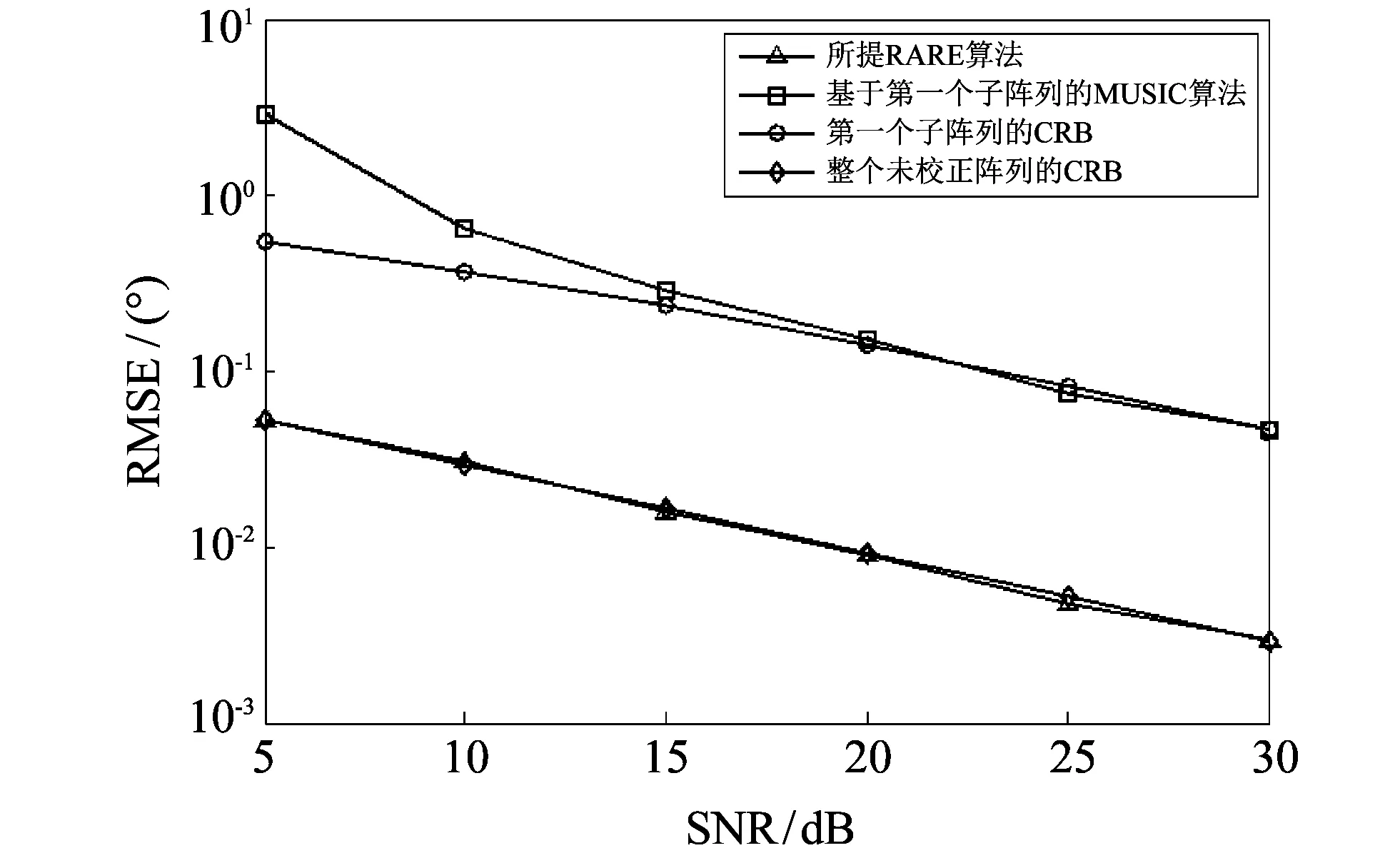
图 1 DOA估计RMSE随SNR变化的曲线Fig.1 The curve of the DOA estimation that RMSE varied with SNR

3.2 子阵列之间参数信息不准确时的角度估计性能分析

分别考虑子阵列位置误差和幅相误差对角度估计的影响. 子阵列位置误差随机均匀地分布在区间[-ρλ,ρλ]. 图2(a)给出了位置误差参数ρ=0.5时DOA估计RMSE随输入SNR变化的曲线. 图2(b)给出了子阵间的幅相误差对DOA估计的影响. 幅度和相位误差分别均匀分布于区间[0.8,1.2] 和[-π/10,π/10]. 从图2可以看出， 子阵列之间参数误差使得基于整个阵列的MUSIC算法性能严重下降. 然而， 所提RARE算法能够稳健地对抗这些误差， 并给出了最好的估计结果. 固定SNR=10 dB， 图3给出了与图2参数误差相同时的空间谱函数.

图 2 子阵参数误差对DOA估计的影响Fig.2 The influence of subarray parameter errors on DOA estimation

图 3 子阵参数误差对空间谱的影响Fig.3 The influence of subarray parameter errors on spatial spectrum

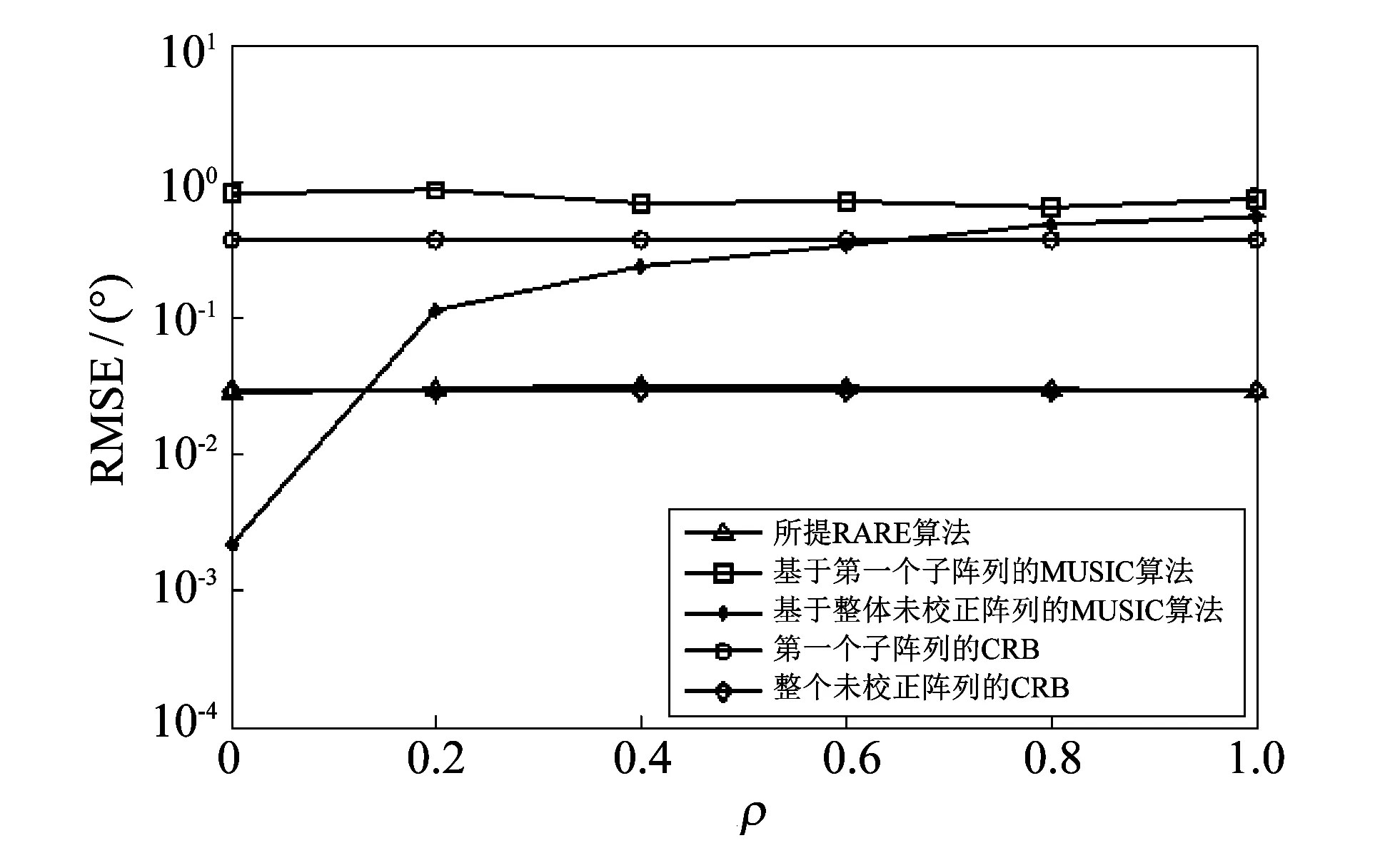
图 4 DOA估计RMSE随子阵位置误差变化的曲线Fig.4 The curve of the DOA estimation that RMSE varied with subarray position error

从图3可以看到子阵之间的参数误差使得基于整个未校正阵列的MUSIC算法的谱峰发生畸变， 影响了MUSIC算法的估计精度， 但是MUSIC算法的分辨率仍然高于所提RARE算法. 图4给出SNR=10 dB时DOA估计RMSE随子阵位置误差变化的曲线. 由图4可以看到随着子阵位置误差变大， 基于整个阵列的MUSIC算法的性能下降很快， 而所提RARE算法不受子阵位置误差变化的影响. 当没有子阵位置误差时， MUSIC算法的性能要远远好于所提RARE算法. 这是由于MUSIC算法可以利用整个阵列的信息， 而所提RARE算法只利用了阵列的部分信息.

4 结 论

本文研究了子阵部分校正时的分布式子阵MIMO雷达角度估计算法. 假设每个子阵的导向矢量已知， 而子阵间的参数是未知或部分已知. 利用分布式子阵MIMO雷达虚拟导向矢量的特殊形式， 用秩亏思想构造RARE角度估计算法可以不需要利用子阵间未知参数信息， 从而仅仅利用已知的阵列信息进行角度估计. 所提算法的有效性通过仿真进行了验证.

[1]陈浩文， 黎湘， 庄钊文. 一种新兴的雷达体制——MIMO雷达[J]. 电子学报, 2012， 40(6)： 1190-1198. Chen Haowen, Li Xiang, Zhuang Zhaowen. A rising radar system——MIMO radar[J]. Acta Electronica Sinica, 2012， 40(6)： 1190-1198. (in Chinese)

[2]Li J, Stoica P. MIMO radar with colocated antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5)： 106-114.

[3]孙理， 朱晓华， 贺亚鹏， 等. 双基地稀疏阵列MIMO雷达快速多目标定位方法[J]. 电子与信息学报， 2013, 35(5)： 1142-1148. Sun Li, Zhu Xiaohua, He Yapeng, et al. Fast multi-target localization with sparse array in bistatic MIMO radar[J]. Journal of Electronics & Information Technology, 2013, 35(5)： 1142-1148. (in Chinese)

[4]刘源, 王洪先, 纠博, 等. 米波MIMO雷达低空目标波达方向估计新方法[J]. 电子与信息学报, 2016, 38(3)： 622-628. Liu Yuan, Wang Hongxian, Jiu Bo, et al. A new method for DOA estimation for VHF MIMO radar in low-angle tracking environment[J]. Journal of Electronics & Information Technology, 2016, 38(3)： 622-628. (in Chinese)

[5]梁浩, 崔琛, 余剑. 基于ESPRIT算法的十字型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2016, 38(1)： 80-89. Liang Hao, Cui Chen,Yu Jian. Reduced-dimensional DOA estimation based on ESPRIT algorithm in monostatic MIMO radar with cross array[J]. Journal of Electronics & Information Technology, 2016, 38(1)： 80-89. (in Chinese)

[6]张炜. MIMO雷达自适应波束形成与角度估计算法研究[D]. 北京： 北京理工大学, 2014.

[7]See C M S, Gershman A B. Direction-of-arrival estimation in partly calibrated subarray-based sensor arrays[J]. IEEE Transactions on Signal Processing, 2004, 52(2)： 329-338.

[8]Elkader S A, Gershman A B, Wong K M. Rank reduction direction-of-arrival estimators with an improved robustness against subarray orientation errors[J]. IEEE Transactions on Signal Processing, 2006, 54(5)： 1951-1955.

[9]符博博, 郑娜娥, 胡捍英. 单基地MIMO雷达中基于改进传播算子的二维DOA估计算法[J]. 信号处理, 2016, 32(4)： 438-443. Fu Bobo, Zheng Nae, Hu Hanying. A two-dimensional DOA estimation algorithm based on improved propagator for monostatic MIMO radar[J]. Journal of Signal Processing, 2016, 32(4)： 438-443.(in Chinese)

[10]李小波, 张正言, 王挺, 等. 双基地MIMO雷达相干目标的角度快速估计算法[J]. 信号处理, 2016, 32(3)： 370-377. Li Xiaobo, Zhang Zhengyan, Wang Ting, et al. Target rapid location of coherent target for bistatic MIMO radar[J]. Journal of Signal Processing, 2016, 32(3)： 370-377.(in Chinese)

DOA Estimation in Subarray-Based MIMO Radar with Distributed Inter-Subarray Calibration

DANG Chan-juan1, ZHANG Wei2, HU Yu-xing3

(1. School of Physics and Electronic Science, Datong University, Datong 037009, China;2. Science and Technology on Electronic Information Control Laboratory, Chengdu 610036, China;3. School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China)

The problem of direction-of-arrival (DOA) estimation in partially calibrated multi-input multi-output (MIMO) array composed of multiple subarrays was studied by using the rank reduced estimator (RARE). By utilizing a specific structured model of virtual steering vector of the subarray-based MIMO arrays, the proposed method obtains the DOA estimation by using the RARE without the information of intersubarray calibration, realizes the efficient utilization of the array, improves the resolution and location accuracy. To evaluate the performance of the proposed estimator, the corresponding stochastic Cram’er-Rao bound (CRB) was derived. Computer simulations demonstrate the effectiveness and validity of the proposed estimator when the inter-subarray parameters were completely or partly unknown.

direction-of-arrival estimation; multi-input multi-output radar; subarray; rank reduction estimator

2016-09-27

山西大同大学校级青年科学研究资助项目(2015Q13)； 国防预研基金资助项目； 高动态低信噪比检测技术研究资助项目(W16GY00010)

党婵娟(1989-)， 女， 助教， 硕士， 主要从事信号与信息处理的研究.

1673-3193(2017)02-0217-04

TN95

A

10.3969/j.issn.1673-3193.2017.02.021