基于精确响应控制的子阵波束赋形算法

彭伟来,张学敬,张 炜,何子述

(1.电子科技大学电子工程学院,四川成都611731;2.电子信息控制重点实验室,四川成都610036)

0 引言

阵列信号处理作为信号处理的一个重要分支,具有波束控制灵活、信号增益高、抗干扰能力强和空间分辨能力高等优点[1]。而波束赋形是阵列信号处理的一个重要研究方向,其研究广泛应用于无线通信、声呐、雷达和麦克风语音阵列处理等领域[2-9]。经过多年研究,学者们提出了许多波束赋形算法。道尔夫-切比雪夫方法可在主瓣宽度确定的情况下来获得最低的旁瓣电平,但该算法只适用于均匀阵列[10]。对于非均匀任意阵列,遗传算法[11]、粒子群算法[12]、模拟退火算法[13]等全局优化变量的算法被提出来。然而,由于这类算法的计算复杂度较高、耗时间较长,使得在实际工程中无法得到广泛应用。另外,随着凸优化理论的发展,利用凸优化工具实现波束赋形的方案被广泛采用并取得了一定成果。如二阶规划法和半正定规划算法[14],可以解决阵列带来的不确定性,具有较强的稳健性。但上述算法均无法实现波束响应的灵活控制,针对此问题,文献[15]提出一种基于自适应理论的精确阵列响应控制(Accurate Array Response Control,A2RC)算法。该算法简单灵活,可以实现任意角度的精确响应控制以及任意形状的波束赋形。

尽管如此,上述算法需要在各个阵元上施加移相器,无法应用于分子阵的阵列。实际上,对于大型相控阵,由于物理体积和成本因素不可能在每一阵列单元均采用延时器,故通常都采用子阵划分的方法实现阵列馈电,这不仅使得整个天线阵列的结构简单、成本降低,而且阵列的方向特性又能得到保证[16]。

子阵划分后对子阵级数字波束的研究目前主要在于子阵级波束形成,对波束指向及多波束比较关注,大多基于粒子群和基因遗传等复杂算法[17-18]。对如何控制子阵级波束旁瓣响应的研究较少,针对该问题,本文考虑均匀划分子阵结构阵列,提出了一种基于A2RC的子阵波束赋形方法。该算法通过使用A2RC算法设计能够满足子阵级期望归一化方向图的子阵级最优权向量,使输出的子阵方向图能够满足给定的输出期望方向图,达到精确控制划分子阵后阵列输出波束的阵列响应值的目的。所提算法能够精确控制子阵划分的输出波束阵列响应值,满足多种波束设计要求,具有通用性及简单灵活性,可用于解决实际工程中的对子阵的波束赋形问题。

1 子阵划分模型

假设均匀线阵阵元个数为M,阵元间距为d,则其阵元级导向矢量a(θ)为

式中,ϕ=2πdsinθ/λ为阵元间的空间相位差。

由于大型相控阵中阵元通道数多,进行阵元级通道处理成本较高,且物理硬件上也较难实现,实际工程应用中通常需要进行子阵划分。考虑较简单常用的均匀划分形式,若将均匀线阵均匀划分为L个子阵,第l个子阵包含Nl个阵元,其示意图如图1所示。图中,表示对子阵的子阵级加权,(·)∗表示对括号内容取共轭。将均匀线阵划分为子阵的变换矩阵,为L×M维矩阵:

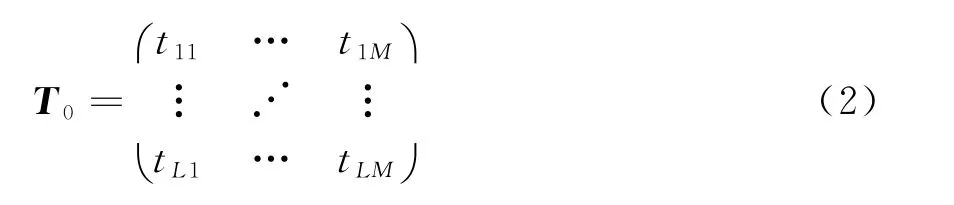
图1 均匀划分子阵结构

变换矩阵中元素tij取值非0即1,每一行代表一个子阵,每行中的非零值个数代表子阵所包含阵元个数。假设波束指向为θ0时,其中子阵变换矩阵应包含阵元级的移相器加权ϕele(θ0),目的是为了使波束指向期望的波束方向θ0。包含了子阵划分效果和阵元级移相器加权效果的变换矩阵为

式中,diag(·)为对角化运算符,wele为阵元级加权。信号波长为λ时,其表达式为

子阵级加权为wsub=[w0w1…wL-1]T,其中[·]T表示转置。子阵级导向矢量asub(θ)可由阵元级导向矢量a(θ)变换得到:

则对应划分子阵后输出的子阵方向图可表示为

式中,(·)H为共轭转置符号。那么基于子阵的波束赋形问题即是通过设计合适的子阵级权向量wsub使得输出的子阵方向图满足特定要求。接下来将提出一种子阵级的波束赋形方法来解决此问题。

2 子阵A 2 RC波束赋形

由第1节可知,对于均匀划分的子阵,只要设计出合适的子阵级的权向量即可实现对子阵结构阵列的子阵级波束赋形。为了达到这个目的,本文借助A2RC算法[15]对输出的子阵方向图进行精确方向图控制。本节先对A2RC算法进行简单介绍,然后再阐述基于A2RC的子阵级波束赋形算法。

2.1 A2 RC算法

由阵列自适应理论可知,在最大化信干噪比(SINR)情况下的最优权向量为

式中,α为与SINR无关的因子,为噪声加干扰协方差矩阵。考虑单个干扰以及白噪声的情况,Rn+i可以表示为

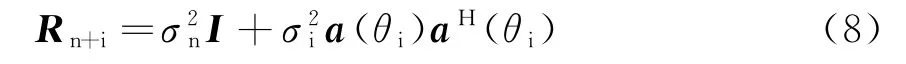
式中,a(θ0)和a(θi)分别为信号和干扰导向矢量,分别为干扰和噪声功率。

将式(8)代入式(7),并结合矩阵求逆引理,可得

式中,‖·‖2表示欧几里得范数为一个常数,可忽略不计。由此,最优权向量可简化为下面形式:

式中,w0定义为初始权向量,为

而其中μ是一个复数,推出为

对于在阵列波束赋形时需要控制多个方向角度的阵列响应,权向量对每个角度都需要迭代更新,其更新迭代表达式为

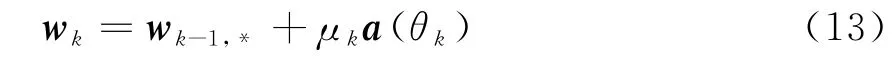
式中,wk-1为第k-1步最优权向量,θk为第k步需要控制响应的角度。定义归一化响应为

要使第k个角度θk的响应为期望值ρk,即

满足式(15)的复数μk在复数平面上的轨迹为以cμ为圆心、以rμ为半径的圆,如图2所示。图中,cμ与rμ皆由a(θ0),a(θk),wk-1和ρk确定。文献[15]证明了为使方向图偏差最小,取μk的模值

图2 μk在复平面分布

最小时,也即是最优的取值为

定义g(v)=v(1)+jv(2)表示将2×1维的向量第一、第二项表示分别为对应为实部和虚部的复数。式(16)中:

式中,Qk(i,j)表示矩阵Qk第i行、第j列对应的元素。Qk可由将式(14)代入式(15)后,即得到式(19)计算:

至此,所求的第k步时,使归一化响应波束方向图的角度θk响应值为ρk的最优权向量为

由式(26)求出的最优权向量即可精确控制阵列响应。

从上述分析可知,A2RC算法能够精确控制任意角度方向的阵列响应,算法简单且具有较强灵活性。下面将阐述借助A2RC算法来实现子阵的波束赋形的算法。

2.2 子阵A2 RC波束赋形原理

基于子阵的波束赋形问题是通过设计合适的子阵级权向量wsub来使得划分子阵后输出的方向图能够满足给定的期望的方向图。本文考虑均匀划分的均匀线阵,其模型结构如图1所示。将均匀线阵均匀划分为L个子阵,则第l个子阵包含Nl个阵元。子阵阵列中单个子阵正好是一个阵元间隔为半波长的均匀线阵,其导向矢量为

当波束指向为θ0时,单个子阵的静态权向量为

由此可以定义单个子阵的阵元的静态归一化方向图:

阵列划分为子阵后的通道阵列也是一个阵元间隔为Nl个半波长的均匀线阵,用此通道阵列直接接收信号时的导向矢量为

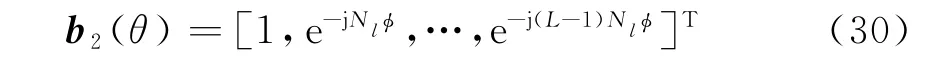
同样地,波束指向为θ0时,阵列的静态权向量为

定义此通道阵列的归一化方向图为

从整个阵列划分子阵来看,L个单一子阵接收信号叠加后,再经L个子阵级的权向量加权,最终得到阵列输出。在这里,令子阵输出的归一化方向图为

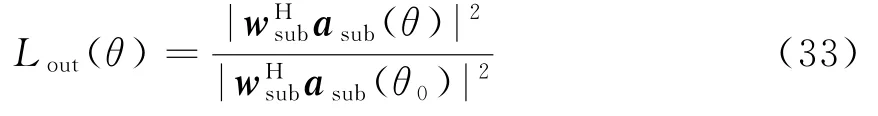
由第1节可知,子阵级导向矢量asub(θ)可由下式得出:

而其中:

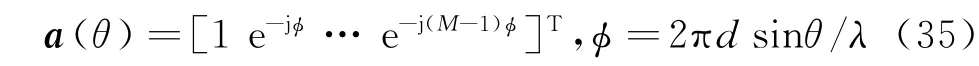
为阵元级阵元导向矢量。将T0,wele,a(θ)代入式(34)中可得

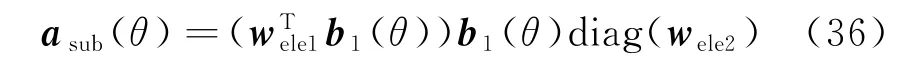
由矩阵理论可知,diag(wele2)(diag(wele2))H=EL×L,EL×L为L×L维单位矩阵;又由wele1,b1(θ)分别为单个子阵中阵元静态权向量、导向矢量,此两项内积亦为一个复数。将式(36)代入式(33)中,可得

由式(37)可以看出,子阵输出归一化方向图可由单个子阵中阵元的归一化方向图和子阵级的归一化方向图表示。只要选择合适的子阵级权向量就可以得到划分子阵后输出归一化方向图。

通过合适的子阵划分,式(37)中左边项为给定的阵列输出期望归一化方向图Ldes(θ);右边第一项L0(θ)由划分子阵结构确定的单个子阵的静态方向图,且为已知;右边第二项为可求项,求出的为子阵级期望归一化方向图,记作Lsub-des(θ)。将子阵级静态方向图调整到能够满足式(32)确定的Lsub-des(θ)即可在输出端得到满足给定的期望归一化方向图,即把在输出端得到归一化期望方向图转化为求满足子阵级归一化期望方向图的子阵级权向量的问题。而子阵级静态归一化方向图由式(38)给定:

在第k步中,从中判断出第k次需要控制的角度及其对应的期望响应值ρk。则其角度对应的子阵级导向矢量为

式中,ϕk=2πdsinθk/λ。利用式(16)可以确定μk,∗,进而可求出第k次最优权向量:

均匀线阵均匀的划分子阵后,对子阵输出波束赋形,只需通过A2RC算法设计出能够满足子阵级期望归一化波束方向图的子阵级权向量wsub即可。表1为子阵级A2RC算法主要步骤。

表1 子阵级A2 RC波束赋形算法步骤

3 仿真

本节对所提算法进行仿真验证,首先针对均匀旁瓣赋形问题,设计了一个旁瓣均匀的输出期望归一化方向图,通过使用所提算法使输出归一化方向图满足了期望要求,简述了算法仿真过程,验证了所提算法的有效性。另外,为了说明所提算法的通用性,考虑了非均匀旁瓣的赋形。

实验一:子阵级A2RC算法原理仿真

假设阵列为均匀线阵,其阵元个数为60,阵元间距为0.5λ,λ为信号波长;将此均匀线阵均匀不重叠的划分为15个子阵,则每个子阵包含阵元个数为4;波束指向为0,其归一化期望方向图的副瓣为均匀副瓣,且不超过-30 d B;初始权向量为b2(θ0)。图3给出了子阵级A2RC算法过程。

首先,从输出归一化期望方向图和划分的单个子阵归一化静态方向图求出子阵级的归一化期望方向图,如图3(a)所示。

然后,开始进入A2RC算法迭代求解合适的子阵级权向量过程。第1步迭代为从子阵级静态方向图中旁瓣值选出高出子阵级归一化期望方向图最大的对应角度值,假设其为θ1,在此实验中θ1=-2.7°。从图3(b)中可以看出,处理的方向图在角度θ1的响应值等于子阵归一化期望方向图对应值。第2步迭代为从上一步中得到的处理的方向图中找到比子阵级归一化期望方向图高的最大旁瓣值所对应的角度值,设其为θ2,此步中θ2=2.8°。从图3(c)中可以看出,在此次处理后的方向图所选中角度处的旁瓣值正好为子阵归一化期望方向图对应角度的旁瓣幅度值。经过10步迭代后,方向图的原本高旁瓣都相对趋于子阵归一化期望方向图旁瓣水平,如图3(d)所示;经过45步迭代后处理的方向图所有旁瓣均不高于子阵归一化期望方向图,达到了较好的效果,如图3(e)所示。

最后,由处理的子阵级归一化方向图和单个子阵方向图即可求得最后输出方向图,如图3(f)所示。

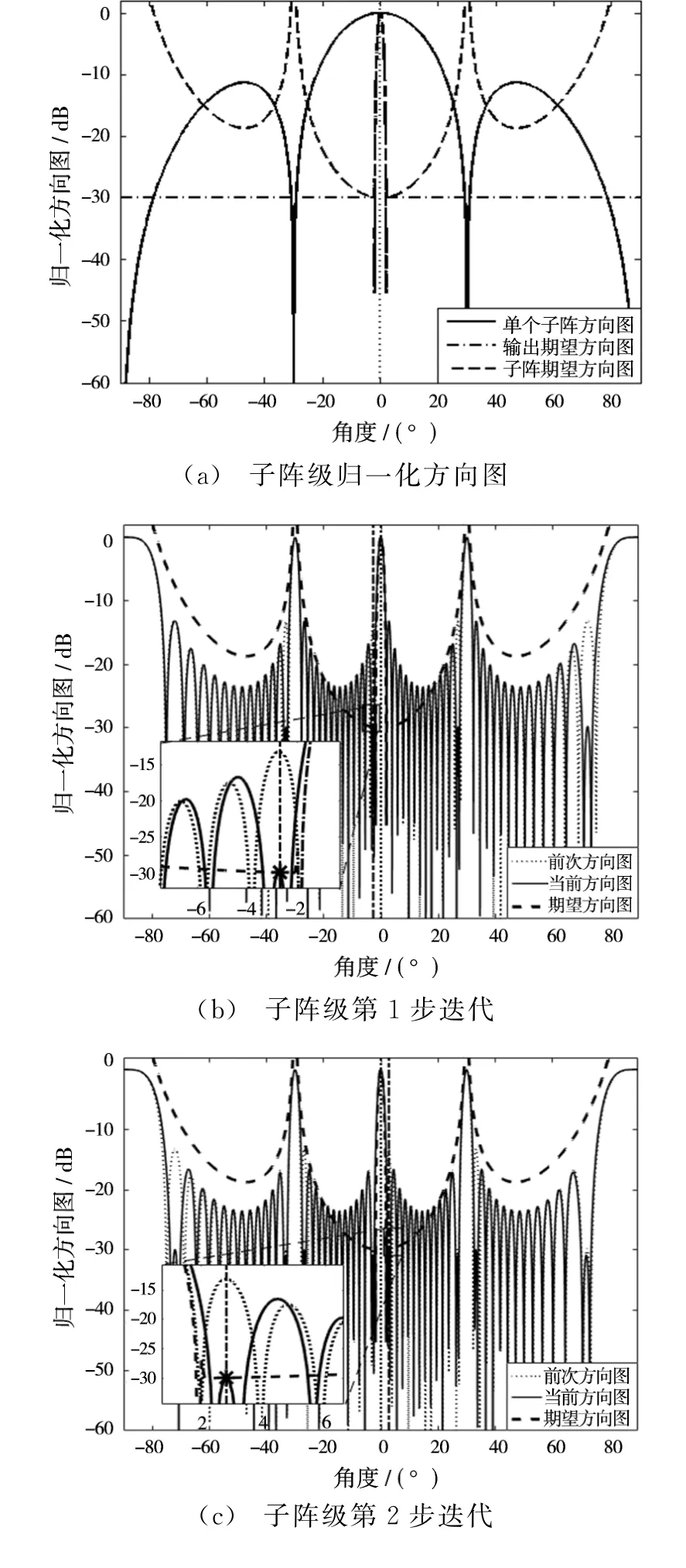
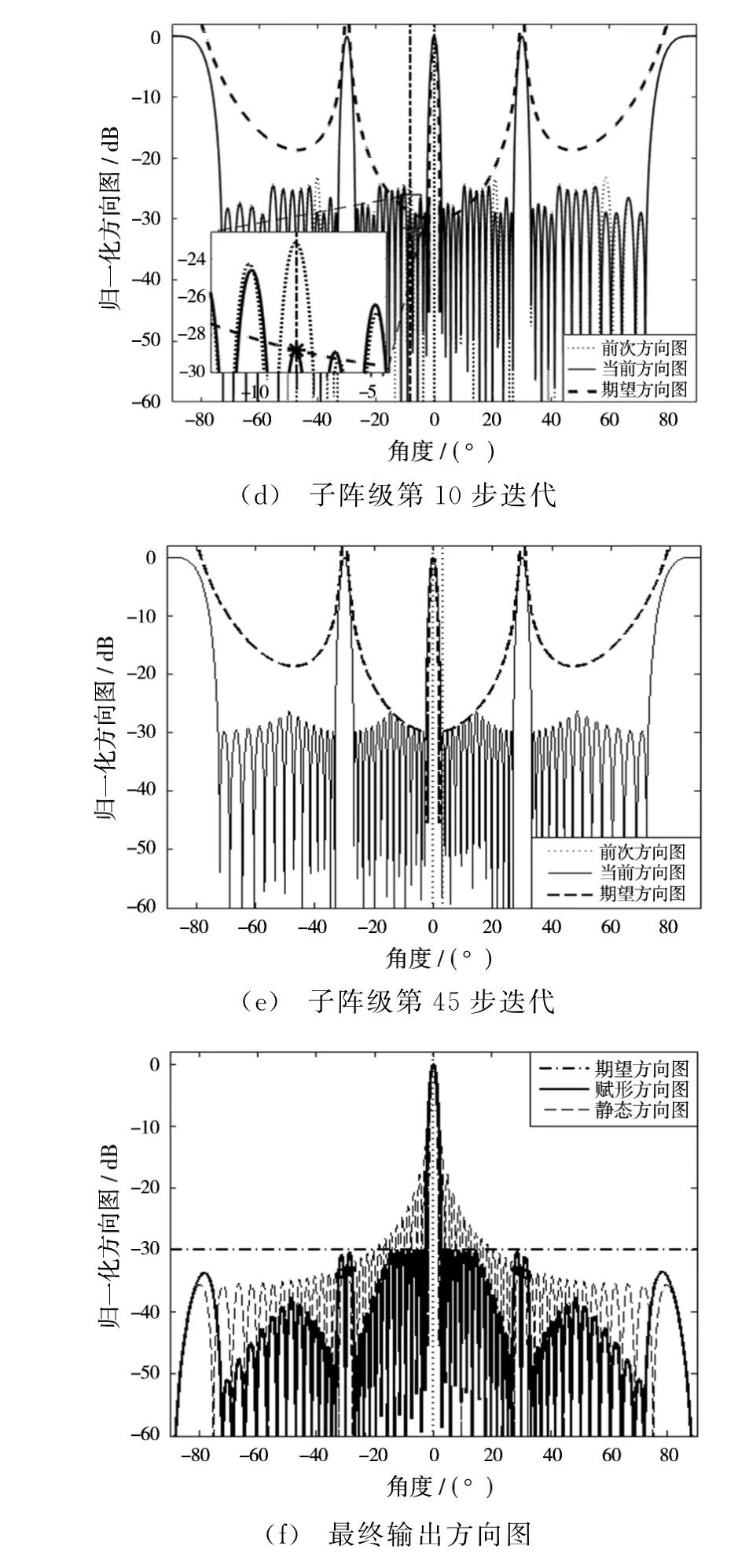
图3 子阵A2 RC算法仿真过程

实验二:非均匀旁瓣控制

假设阵列均匀线阵,其阵元个数为64,阵元间距为0.5λ,λ为信号波长;将此均匀线阵均匀不重叠地划分为16个子阵,则每个子阵包含4个阵元;波束指向为10°;其归一化期望方向图的旁瓣为非均匀旁瓣,在15°～25°之间副瓣不超过-35 d B,旁瓣其他位置不超过-30 dB;初始权向量为b2(θ0)。则其经过子阵A2RC算法波束赋形后,其效果如图4所示。

从图4可以看出,在随机取得波束指向θ0=10°下,非均匀旁瓣在15°～25°角度范围内,其旁瓣幅度值仍然低于期望值,整个波束方向图能够满足给定的期望方向图。本文所提算法在不同波束指向情况下能够有效地控制旁瓣,并且可以满足随意设计的非均匀旁瓣,能够适用不同需求的波束赋形,具有一定的通用性。

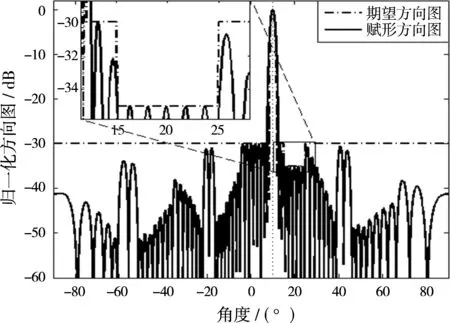
图4 非均匀旁瓣赋形

4 结束语

本文基于A2RC算法提出了一种可以应用于均匀划分子阵的波束赋形方法。该算法把在输出端设计合适权向量满足输出归一化期望方向图问题转化为求取满足子阵级归一化期望方向图的子阵级权向量的问题,借助精确控制阵列响应算法,精确控制子阵级方向图来达到子阵级期望方向图,最终达到子阵输出波束赋形目的。本文所提算法能够在任意波束指向下控制阵列响应,以满足多种复杂旁瓣的期望波束,具有广泛通用性。亦弥补了对均匀划分子阵波束赋形的空白,因均匀划分子阵减少了通道数,此算法具有较高工程应用价值。

[1]PILLAI S U,BURRUS C S.Array Signal Processing[M].New York:Springer-Verlag,1989.

[2]SCHOLNIK D P.A Parameterized Pattern-Error Objective for Large-Scale Phase-Only Array Pattern Design[J].IEEE Trans on Antennas and Propagation,2016,64(1):89-98.

[3]SAFAAI-JAZI A,STUTZMAN W L.A New Low-Sidelobe Pattern Synthesis Technique for Equally Spaced Linear Arrays[J].IEEE Trans on Antennas and Propagation,2016,64(4):1317-1324.

[4]PALMA L D,CLEMENTE A,DUSSOPT L,et al.Radiation Pattern Synthesis for Monopulse Radar Ap-plications with a Reconfigurable Transmitarray Antenna[J].IEEE Trans on Antennas and Propagation,2016,64(9):4148-4154.

[5]LI Longjun,WANG Buhong.Reducing the Number of Elements in a Pattern Reconfigurable Antenna Array by the Multi-Task Learning[J].IET Radar,Sonar&Navigation,2016,10(6):1127-1135.

[6]KWAK S,CHUN J,PARK D,et al.Asymmetric Sum and Difference Beam Pattern Synthesis with a Common Weight Vector[J].IEEE Antennas and Wireless Propagation Letters,2016,15(1):1622-1625.

[7]FUCHS B,RONDINEAU S.Array Pattern Synthesis with Excitation Control via Norm Minimization[J].IEEE Trans on Antennas and Propagation,2016,64(10):4228-4234.

[8]ECHEVESTE J I,GONZÁLEZ DE AZA M A,ZAPATA J.Array Pattern Synthesis of Real Antennas Using the Infinite-Array Approach and Linear Programming[J].IEEE Trans on Antennas and Propagation,2015,63(12):5417-5424.

[9]LIU Yanhui,CHEN Shulin,ZHANG Liang,et al.Determining the Firstnull Mainlobe Region of an Arbitrary Pattern for 2-D Numerical Pattern Synthesis Algorithm[J].IEEE Trans on Antennas and Propagation,2016,64(3):1130-1136.

[10]DOLPH C L.A Current Distribution for Broadside Arrays Which Optimizes the Relationship Between Beam Width and Side-Lobe Level[J].Proceedings of the IRE,1946,34(6):335-348.

[11]HA B V,MUSSETTA M,PIRINOLI P,et al.Modified Compact Genetic Algorithm for Thinned Array Synthesis[J].IEEE Antennas and Wireless Propagation Letters,2016(15):1105-1108.

[12]BOERINGER D W,WERNER D H.Particle Swarm Optimization Versus Genetic Algorithms for Phased Array Synthesis[J].IEEE Trans on Antennas and Propagation,2004,52(3):771-779.

[13]MURINO V,TRUCCO A,REGAZAONI C S.Synthesis of Unequally Spaced Arrays by Simulated Annealing[J].IEEE Trans on Signal Processing,1996,44(1):119-122.

[14]WANG Fan,BALAKRISHNAN V,ZHOU Yuan

ping,et al.Optimal Array Pattern Synthesis Using Semidefinite Programming[J].IEEE Trans on Signal Processing,2003,51(5):1172-1183.

[15]ZHANG Xuejing,HE Zishu,LIAO Bin,et al.A2RC:An Accurate Array Response Control Algorithm for Pattern Synthesis[J].IEEE Trans on Signal Processing,2017,65(7):1810-1824.

[16]高瑜翔,何子述,徐继麟,等.基于旁瓣电平和主瓣偏移的光控线性相控阵列子阵数确定方法[J].电子与信息学报,2005,27(8):1222-1225.

[17]王文昌,李雷,刘春静,等.基于粒子群优化算法的非均匀子阵波束形成技术[J].电子信息对抗技术,2010,25(1):36-40.

[18]江禹生,周勋,刘枫.基于遗传算法的均匀子阵数字多波束形成研究[J].系统仿真技术,2008,4(2):102-106.