混合MIMO 相控阵雷达反向非均匀重叠子阵分割方法*

程天昊，王布宏，李 夏

（空军工程大学信息与导航学院，西安 710077）

0 引言

近年来，混合MIMO 相控阵雷达受到越来越多专家学者的关注［1-2］。作为传统相控阵雷达和MIMO雷达的混合模式，它有效地实现了发射相干处理增益和波形分集增益两者的折中，为平衡两种雷达的性能提供了可行的解决方案。

如何在不增加复杂度的前提下，通过寻求更优的子阵结构和孔径分布，充分发挥两种雷达的性能优势，实现传输相干增益和波形分集增益的最佳折中，是学者们在雷达应用领域研究的热点。文献［3-9］通过对MIMO 雷达发射波形协方差矩阵的设计，从发射信号设计的角度来实现天线方向图的聚焦，但是此类设计往往会导致复杂的约束优化问题，通常没有闭合的解析解。而且与正交波形设计类似，相关波形的常模特性、自相关和互相关特性在实际中往往难以满足要求，同时给系统实现过程中的信号合成和功率放大带来较大的困难。

为了避开复杂的数学优化问题，部分学者提出了混合MIMO 相控阵雷达子阵分割的方法，通过寻求灵活的子阵分割方式，在系统的波形分集增益和发射相干增益之间获得理想折中，其本质上是发射波形协方差矩阵的一种特殊设计方法。对混合MIMO 相控阵雷达而言，阵列结构设计中的子阵分割模式是将两种雷达体制进行结合的基础。发射阵列进行子阵分割，每个发射单元所发射的信号为若干正交波形的线性叠加，可以等价于发射阵列单元信号为特殊的相关信号；再者，混合MIMO 相控阵雷达可以等效为具有聚焦发射方向图的MIMO 雷达。通过发射子阵个数的选择，可以灵活选择发射相干增益和波形分集增益之间的折中程度，进而对雷达性能产生影响。子阵个数越多，发射的正交波形的个数越多，系统的波形分集增益就越强；但是对应的子阵孔径就越小，发射相干增益越弱。反之亦然。

文献［10-12］将阵列划分为几个相同孔径的不重叠子阵，可以等效为若干个相控阵并行工作。这样的阵列结构虽然简单易行，但是子阵孔径会较大幅度地减小，发射相干处理增益会相应降低。为了进一步优化这种结构，文献［1，13-14］将混合MIMO相控阵雷达划分为几个相互重叠的相等孔径子阵（Hybrid Phased-MIMO Radar with Equal Subarrays，HPMR-ES），这样划分的优点是结构相对简单，子阵孔径增大，发射相干增益有了一定幅度的提高。为了进一步扩展子阵孔径，文献［15-17］提出了非均匀重叠子阵分割（Hybrid Phased-MIMO Radar with Unequal Subarrays，HPMR-US）的思路，相比于前两种思路，这种方法不仅能够改善整体方向图，还可以提高信干噪比（Signal to Interference plus Noise Ratio，SINR）。其性能提升的本质在于通过阵元层叠来获取更大的子阵孔径，进而提高发射相干增益，但另一方面，由于所有子阵的首阵元重合，会丢失波形分集增益。而且文中仅仅通过仿真验证了所提方法的优越性，缺乏严谨的理论推导。因此，提出一种反向非均匀重叠子阵分割方法（Hybrid Phased-MIMO Radar with Reversed Unequal Subarrays，HPMR-RUS），在共址MIMO 雷达的基础上，将第一个子阵设置为满阵，后续子阵依次右移，且阵元个数依次减少。这种方法既增强了发射相干处理增益，又保留了波形分集增益，通过公式推导和仿真实验，证明了该方法可以使方向图旁瓣降低、输出信干噪比增大、DOA 估计精度提高。

1 混合MIMO 相控阵雷达传统的重叠分割模式

目前，对于混合MIMO 相控阵雷达线阵来说，重叠分割方式的孔径利用率较高，各个子阵发射互相正交的信号，每个阵元的发射信号为若干正交信号的线性叠加，等价于发射端阵元发射相干信号的共址MIMO 雷达，同时避免了复杂的相关波形设计，降低了系统的实现难度和成本。因此，近年来重叠的子阵分割方式受到越来越多的关注。

1.1 均匀重叠的子阵分割模式

图1 混合MIMO 相控阵雷达均匀重叠子阵分割模式

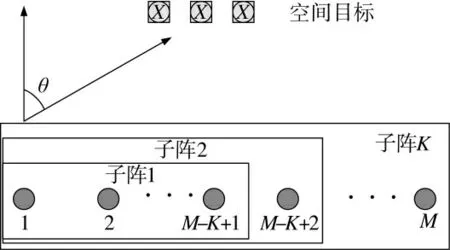
图2 混合MIMO 相控阵雷达非均匀重叠子阵分割模式

由于这种子阵分割方式简单易操作，所以已经被广泛应用于混合MIMO 相控阵雷达的研究。其虚拟导向矢量u（θ）包含相干处理矢量c（θ）、波形分集矢量d（θ）和接收导向矢量b（θ）3 部分。但是随着子阵个数K 的增加，子阵孔径随之减小，造成发射相干处理增益的降低。对于孔径的利用率不足，因此，这种方法正逐渐被非均匀的子阵分割方式取代。

1.2 非均匀重叠的子阵分割模式

我们考虑一个由M 个发射阵元和N 个接收阵元组成的混合MIMO 相控阵雷达系统，阵元间距为半波长，子阵个数为K。按照非均匀重叠子阵模式对发射阵列进行子阵划分。每个子阵发射功率相同。那么虚拟导向矢量u（θ）可以用Kronecker 积⊗表示为：

2 反向非均匀重叠的混合MIMO 相控阵雷达分割模式

2.1 信号模型

针对非均匀重叠子阵分割方法带来的波形分集增益损失问题，如何在保留已有高相干增益的基础上，通过设计一种合理的子阵分割方法，使雷达系统获得较高的波形分集增益，是解决现有子阵分割方法瓶颈问题的关键。基于上述考虑，提出了一种反向的非均匀重叠子阵分割方法。

考虑由M 个发射阵元和N 个接收阵元组成的混合MIMO 相控阵雷达系统，具体如图3 所示。

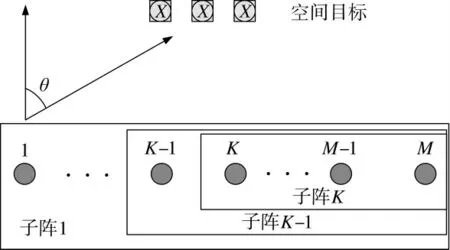
图3 混合MIMO 相控阵雷达的反向非均匀重叠子阵分割模式

其中，wk代表第k 个子阵的M×1 维归一化发射波束权值复矢量，每个wk的第1 到第k 个元素都不相同，可以通过对其赋值来实现子阵波束的聚焦。进而在方位角为θ 处的目标反射信号可以表示为：

对于空间中位于方位角为θs处的目标，以及D个干扰源，N×1 维接收信号可以表示为：

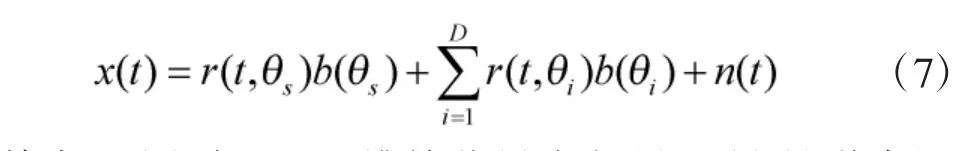
其中，b（θ）为N×1 维接收导向矢量，n（t）是噪声矩阵对接收信号的影响。进一步匹配滤波之后，KN×1维虚拟数据矩阵为：

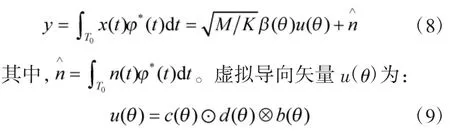
这种反向分割模式所产生的虚拟导向矢量，相比于非均匀重叠子阵分割方法，增加了波形分集矢量d（θ）。虽然在维度上并没有变化，但是由于Hadamard 乘积的作用，使得虚拟导向矢量u（θ）的内部的值发生了变化，从后续的分析中可以看出，u（θ）的改变起到了提升阵列整体性能的作用。

2.2 波束形成和SINR

在阵列权值矩阵的设计上，对于混合MIMO相控阵雷达而言，可以采用常规和自适应波束形成算法。

在发射端，上行波束形成权值矢量可以定义为：

2.3 方向图分析

归一化综合方向图可以表示为：

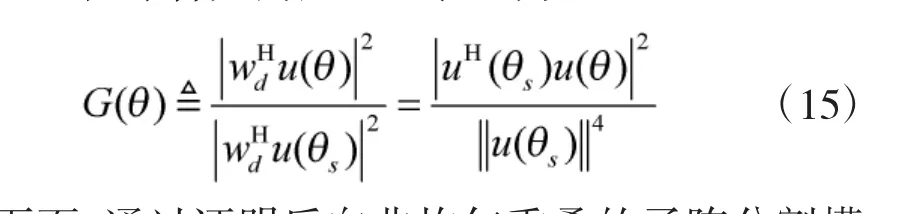
下面，通过证明反向非均匀重叠的子阵分割模式下，总体方向图的最高旁瓣低于非均匀重叠的子阵分割模式下的最高旁瓣，从而证明本文提出算法的优越性。也就是要证：

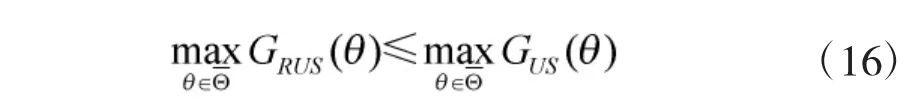
即：

而对于非均匀和反向非均匀重叠分割的混合MIMO 相控阵线阵来说，子阵的不同会带来发射导向矢量和子阵元数目的不一致，进而带来发射相干方向图和分集方向图的不同，因此，在此需要分别对K 个子阵的发射方向图求和。即：

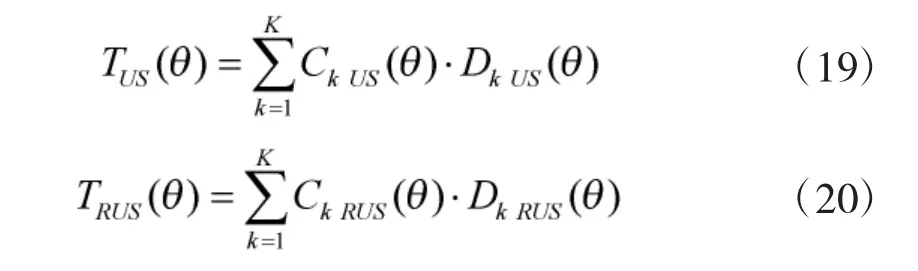
在不等式（17）右侧，非均匀重叠子阵分割的情况下，第k 个子阵的发射相干方向图为：

观察可知是一个等比数列的求和式，因此，式（23）可化简为：

对比非均匀和反向非均匀情况下的分集方向图：

通过分析可以看出，从另一个角度来看，可以认为反向非均匀重叠的子阵分割与非均匀重叠的子阵分割在结构上是一致的，不同的是，在非均匀分割方式中，从小孔径子阵到大孔径子阵，信号的相位依次增大；在反向非均匀分割方式中，从小孔径子阵到大孔径子阵，信号的相位依次减小。由于输入信号的不同，带来了不同的阵列性能。

3 验证

表1 单个子阵发射方向图随值变化的对比表

采用传统波束形成的3 种子阵分割方式的方向图如图4 所示。结果表明，由于发射孔径的扩展，HPMR-RUS 以及HPMR-US 方式获得的最大发射增益优于HPMR-ES 方式。图4 给出了用于3 种子阵分割模式下的总体方向图。可以看出，由于非均匀重叠的方式在发射端获得了更高的相干处理增益，与均匀重叠的子阵分割方式相比，HPMR-RUS以及HPMR-US 的子阵分割方式的整体方向图具有更低的旁瓣和更窄的主瓣。

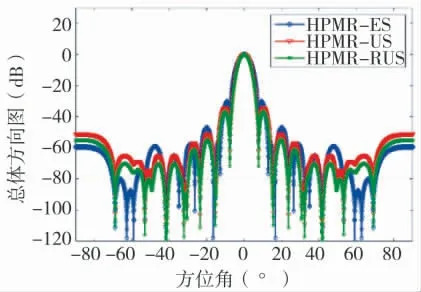
图4 采用传统波束形成算法的波束方向图

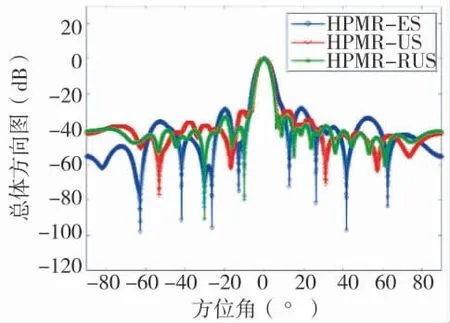
图5 采用MVDR 波束形成算法的波束方向图

MVDR 波束形成的结果如图5 所示。可以看出采用反向非均匀重叠分割方式的雷达在旁瓣区域的表现优于另外两种方式，且相比于HPMR-US 方式具有较好的干扰抑制能力。这种性能上的提高是由于发射端子阵孔径增大，带来更好的波束聚焦能力，同时没有损失波形分集增益，从而使得方向图效果最佳。

图6 采用传统和MVDR 波束形成算法的输出SINR 曲线图

在图6 中，给出了3 种方案的输出信干噪比随信噪比的变化曲线，可以看出，无论是在传统还是MVDR 波束形成算法下，输出SINR 的值总是遵循HPMR-RUS 优于HPMR-US，更优于HPMR-ES 的规律。这是在HPMR-RUS 情况下，两种增益增大所带来的结果。

图7 3种DOA 估计的RMSE 对比图

最后，给定空间中位于-10°，0°，10°的3 个目标进行MUSIC 谱估计［8，19］，所得的均方根误差（Root-Mean-Sequare Error，RMSE）曲线图（该曲线为3 个目标的RMSE 平均值）如图7 所示。可以看出，使用HPMR-RUS 分割模式雷达的DOA 估计精度优于使用HPMR-US 分割模式的雷达，更优于使用HPMR-ES 分割模式的雷达。因此，可以认为所提出的这种子阵分割方法能有效提高阵列的DOA 估计精度。

在实际应用中，相比于HPMR-ES 的子阵分割，HPMR-US 的子阵内包含更多的阵元，也就意味着每个阵元发射的叠加的正交信号数目更多，因此，设计复杂度稍有增加。我们所提出的这种HPMR-RUS 结构是对HPMR-US 结构的翻转，相比于HPMR-ES 更为复杂一些，但是和HPMR-US 的复杂度完全相同，虽然看似两者结构类似，但是在波形分集增益上有着本质的差别。

4 结论

本文提出了一种反向非均匀重叠子阵分割方法，它将子阵分为完全重叠且孔径不同的若干子阵。每个子阵发射相互正交的波形，子阵内部工作在相控阵模式。这种HPMR-RUS 方法相比于HPMR-ES 方法，拥有相同的分集增益和更高的相干处理增益；与HPMR-US 方法相比，拥有相同的相干处理增益和波形分集增益。因此，是一种可以同时兼顾两种增益的子阵分割方式。由于两种发射端增益的优化，能够降低方向图旁瓣电平，提高输出信干噪比，以及提高DOA 估计精度。仿真结果验证了提出的HPMR-RUS 方法的优越性。