考虑感染期的院内抗生素耐药菌传播模型及其稳定性分析

冯丹丹， 薛亚奎

(中北大学 理学院， 山西 太原 030051)

考虑感染期的院内抗生素耐药菌传播模型及其稳定性分析

冯丹丹， 薛亚奎

(中北大学 理学院， 山西 太原 030051)

针对感染期对院内抗生素耐药菌传播的影响, 结合院内感染的特性， 建立了一类带有感染期时滞， 同时考虑患者间直接传播及医患间间接传播抗生素耐药菌的传染病模型. 引入感染期时滞的同时， 考虑患者经过感染期后仍在院内的概率为e-μτ. 运用确定疾病暴发阈值R0、 Routh-Hurwitz判据、 Lasalle-Liapunov不变集原理等经典方法， 证明了当R0<1时， 对于任意的时滞τ≠0， 无病平衡点是局部以及全局渐近稳定的； 当R0>1时， 地方病平衡点存在且唯一， 对于任意的时滞τ≠0， 地方病平衡点是局部以及全局渐近稳定的. 即在该模型中感染期时滞并不影响平衡点的稳定性， 并通过数值模拟验证了结论的正确性.

时滞模型； 抗生素耐药性； 医媒； 感染期

0 引 言

对于院内感染的研究， 最早开始于Homels提出由医生带给产妇的感染； 19世纪中叶， Lister阐明了细菌与感染之间的关系， 并首次提出消毒的概念； 之后南丁格尔创始了目前还在使用的无菌技术， 医院感染才得到有效地控制[1]. 国内对院内感染方面的研究始于1986年， 提出了院内感染管理， 并在2003年“SARS”事件后得到加强. 目前， 世界各国院内感染的发生率一般在5%～15%， 且随国家经济水平差异而有所不同. 根据2009年中国医院感染监测网显示的调查结果， 我国院内感染发生率约为9.7%. 医院感染已成为住院病人死亡的重要病因之一， 住院病人中1/3～1/4 直接死于医院感染， 并造成医疗花费的增加[2]. 然而， 在引起院内感染的众多病菌中， 抗生素耐药菌是其中重要的部分. 由于抗生素的不合理使用甚至滥用、 新抗生素的研发进展缓慢等现状， 细菌耐药的问题越来越突出， “超级菌”也接连不断地出现. 联合国卫生组织在2014年6月发文称“不控制细菌耐药， 可能无药可用”， 可见抗生素耐药菌成为引起院内感染的十分危险的部分. 预防和控制抗生素耐药菌在院内的传播， 不仅是保障住院患者安全、 提高医疗质量以及维护医务人员职业健康的一项重要工作， 也是现代医院管理中的一项重大课题.

运用数学模型研究抗生素耐药菌在医院内的传播机制、 控制要素、 预防措施等， 一直是院内感染研究的一个重要方法[3-8]. 近10年内的相关文献， 主要分为3类： 一类是综述型文献， 一些学者将前人的经典模型进行系统地罗列和总结[3-5]； 一类是完善型文献， 由于院内抗生素耐药性传播仓室模型具有高维度、 多参数的特点， 受到当时数理论证水平的局限， 前人所建模型能够进行完整稳定性分析的非常少， 因此一些学者专注于完善模型数理论证的工作； 另一类是改进型文献， 一些学者将前人的模型根据院内感染现状进行改进， 有针对性地对模型进行数理论证， 为院内感染控制提出具体建议. 如D’Agata E M C将医护人员分为未携带、 只携带非耐药菌、 同时携带非耐药菌和耐药菌、 只携带耐药菌等4类， 将病人分为未感染、 仅感染了非耐药菌、 感染的非耐药菌转化为耐药菌、 同时感染了非耐药和耐药菌、 仅感染了耐药菌等5类， 建立了随机点对点(Individual-based Models， IBM)模型[6], 突破了仓室模型高度一般化的状况， 并最终通过数值模拟的方法得出早期治疗可以缩短患病期的结论. 此外， S. Bonhoeffer分别建立了运用单一抗生素疗法治疗和运用多重抗生素疗法治疗抗生素耐药性的两种仓室模型， 开启了运用数学模型论证不同疗法对疾病传播影响的研究[7]. 13年后Hong-Rui Sun等运用常微分方程的定性及稳定性理论对S. Bonhoeffer的数学模型进行了量化分析， 通过严密的数学论证支撑了S. Bonhoeffer得出的结论——多重抗生素疗法对疾病的控制比单一循环疗法的效果好得多[8].

然而S. Bonhoeffer 的模型将患者之间的直接传播认为是抗生素耐药菌的唯一传播途径， 忽略了医护人员作为媒介在抗生素耐药菌传播过程中的重要作用， 这与医院内传染的特点不相符. 因此本文建立了一类同时考虑病人间的直接传染和医患间的间接传染模型[9]， 并运用文献[10-14]中的平衡点稳定性的论证方法， 来研究感染期在模型中对抗生素耐药菌传播的影响， 希望能从感染期这个角度为现下预防抗生素耐药菌在医院内传播工作提供理论参考.

1 时滞模型的建立

本文将患者从感染抗生素耐药菌后到被检测出或者表现出感染症状的时间段称为感染期， 用τ表示. 由于所研究的患者均为住院患者， 而经过感染期后存在有患者已经出院的可能， 因此我们需要考虑经过感染期后， 病人仍在医院内的概率e-μτ， 其中μ表示住院患者的出院率.我们将住院患者分为3类， 分别为： 未感染抗生素耐药菌的病人， 用Xp表示， 又称易感者； 感染了抗生素耐药菌的病人， 用Yp表示， 又称染病者； 其抗生素耐药性已经被治愈的病人， 用R表示， 又称恢复者， 住院患者的总和用Np表示. 我们将医护人员分为2类， 分别为： 未携带抗生素耐药菌的医护工作者， 用Xh表示， 又称未携带病菌医护人员； 携带了抗生素耐药菌的医护工作者， 用Yh表示， 又称携带病菌医护人员， 医护工作者的总合用Nh表示. 鉴于实际中对从事医护工作的职业技能要求很高， 故这里假设单位时间内医护人员的数量不变. 用Λ表示单位时间内医院新增的病人数.β1表示易感者与携带病菌医护人员接触后被感染的概率， 又称感染率；β2表示未携带病菌医护人员与染病者接触后携带抗生素耐药菌的概率， 又称携带率；p表示染病者被治愈的概率， 又称治愈率；q表示感染者的平均治疗时间；d表示携带病菌医护人员脱离抗生素耐药菌的概率， 又称脱菌率. 研究表明，t时刻抗生素耐药菌感染者的数量依赖于τ个时间单位前未感染抗生素耐药菌的病人数量和接触过这些易感者的携带抗生素耐药菌的医护工作者数量[14]， 因此感染抗生素耐药菌病人的感染项可以表示为β1e-μτXp(t-τ)Yh(t-τ). 然后建立如下时滞模型

考虑到实际情况, 模型中所有的参数都应为正数, 所以设初始条件为

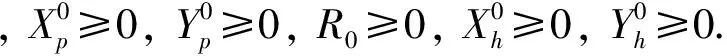
通过求解如下方程

可解得

当且仅当R0>1时, 系统(2)的地方病平衡点E*存在且唯一.

2 平衡点稳定性分析

定理 1 当R0<1时, 对于任意的时滞τ≥0， 系统(2)的无病平衡点E0局部渐近稳定; 当R0>1时,E0不稳定.

证明 如下是系统(2)在无病平衡点处的Jacobian矩阵

对应的基本特征方程为

(λ+μ)[λ2+(d+c)λ+cd-dcR0e-λτ]=0,

显然λ1=-μ为特征方程的负实根, 所有其他的根由方程(3)决定.

化为

1) 当τ=0时, 将方程(4)的两个根分别记作λ2和λ3, 由韦达定理可知

λ2+λ3=-(d+c)<0,λ2×λ3=dc(1-R0),

则当R0<1时特征根均具有负实部， 由Hurwitz判矩可得此时无病平衡点局部稳定. 反之，R0>1时， 无病平衡点不稳定.

2) 当τ≠0时, 将方程(4)经过移项变号后得

记

F(λ)=λ2+(d+c)λ,

这里F(0)=0,G(0)=cd(R0-1). 当R0>1时，G(λ) 的函数曲线与抛物线F(λ)交于第一象限， 因此当R0>1时， 方程(5)一定有一个正实根, 此时系统(2)的无病平衡点不稳定; 当R0<1时, 同理可知方程(5)无非负实根.

现假设方程(5)有具有非负实部的复数根, 则从τ=0到τ>0的过程中必存在一个τ*>0, 使得方程(5)有一对纯虚根. 不妨设λ=ωi (ω>0) 是方程(5)的一个纯虚根, 代入方程(5)得

-ω2+(d+c)ωi=cd[R0cos(ωτ)-1]-

cdR0sin(ωτ)i.

分离实虚部得

(d+c)ω=-dcR0sin(ωτ).

对方程(6)和(7)两边平方消去三角函数, 得到一个关于ω的四次方程

令z=ω2, 则可得

综上可得,R0<1时,E0在可行域内是局部渐近稳定，R0>1时，E0在可行域内不稳定.

定理 2 当R0≤1时, 对任意的时滞τ≥0， 系统(2)的无病平衡点在可行域内是全局渐近稳定的.

证明 首先, 把系统(2)的解转化为xt,xt=(Xp(t+θ),Yp(t+θ),Yh(t+θ)), 其中σ∈[-τ,0].

定义 Liapunov 函数如下

V1(xt)=β2KYp(t)+cYh(t)+

β1β2Ke-μτXp(t)Yh(t)<-β2cYh(t)Yp(t)-

-(β2c+β1β2Ke-μτ)Yh(t)Yp(t)+

定理 3 当R0>1时， 对于任意的时滞τ≥0， 系统(2)的地方病平衡点E*局部渐近稳定.

证明 同定理1的证明， 如下是系统(2)在地方病平衡点处的Jacobian矩阵

对应的特征方程形式为

λ3+P1λ2+P2λ+P3=

其中：

1) 当τ=0时, 方程(9)可化为

λ3+(P1-Q1)λ2+(P2-Q2)λ+

其中：

(P3-Q3)=cμd+cμβ2>0,

则在E*处特征方程(10)没有非负实部的特征根, 系统(2)在地方病平衡点E*处局部渐近稳定.

2) 当τ≠0时, 假设特征方程(9)有纯虚根λ=ϖi， 代入方程(9)中得

-ϖ3i-P1ϖ2+P2ϖi+P3=

(-Q1ϖ2+Q2ϖi+Q3)e-μτ[cos(ϖτ)-sin(ϖτ)i],

将上式分离实部和虚部， 并将得到的两个式子做平方和运算得到如下方程

其中：

设式(11)中ϖ2=z, 则式(11)可化简成

经化简可得

c2+μ2>0,

根据韦达定理可知不存在ϖ使得ϖ2=z. 综上可得, 系统(2)在地方病平衡点E*处局部渐近稳定.

定理 4 当R0>1时， 对于任意的时滞τ≥0， 系统(2)的地方病平衡点E*全局渐近稳定.

证明 构造Liapunov函数

令a1=a2, 则

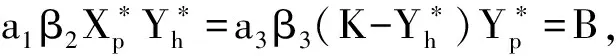
综上得证系统(2)的地方病平衡点, 对于任意τ≥0， 全局渐近稳定.

3 数值模拟

为了验证上文得到的系统(2)平衡点是全局渐近稳定的结论， 应用MATLAB对系统(2)进行数值模拟， 结果如图 1， 图 2 所示.

由图 1 和图 2 可以看到随着时间的逐渐推移， 感染抗生素耐药菌的患者人数逐步达到一个稳定的数值后不再波动. 可见系统(2)在R0满足一定条件时， 无病平衡点和地方病平衡点对于任意的τ≥0都是全局渐近稳定的， 说明上文得出的稳定性结论是正确的.

为了了解患者的出院率μ, 患者的感染率β1, 医护工作者的携带率β2对感染抗生素耐药菌患者人数的影响， 以及β1,β2对基本再生数R0的影响， 分别做了4幅模拟图， 如图 3 所示.

图3(a)中显示，Yp的值随出院率的增加呈下降趋势， 下降速度先快后慢； 图3(b)中显示，Yp的值随患者感染率的增加呈上升趋势， 上升速度先快后慢； 图3(c)中显示， 不论医护人员的携带率高低， 对Yp的值的影响是基本相同的.

图 1 R0<1时, 系统(2)在无病平衡点处全局渐近稳定Fig.1 When R0<1, the system (2) is global stability at the disease-free equilibrium

图 2 R0>1时, 系统(2)在地方病平衡点处全局渐近稳定Fig.2 When R0>1, the system (2) is global stability at the endemic equilibrium

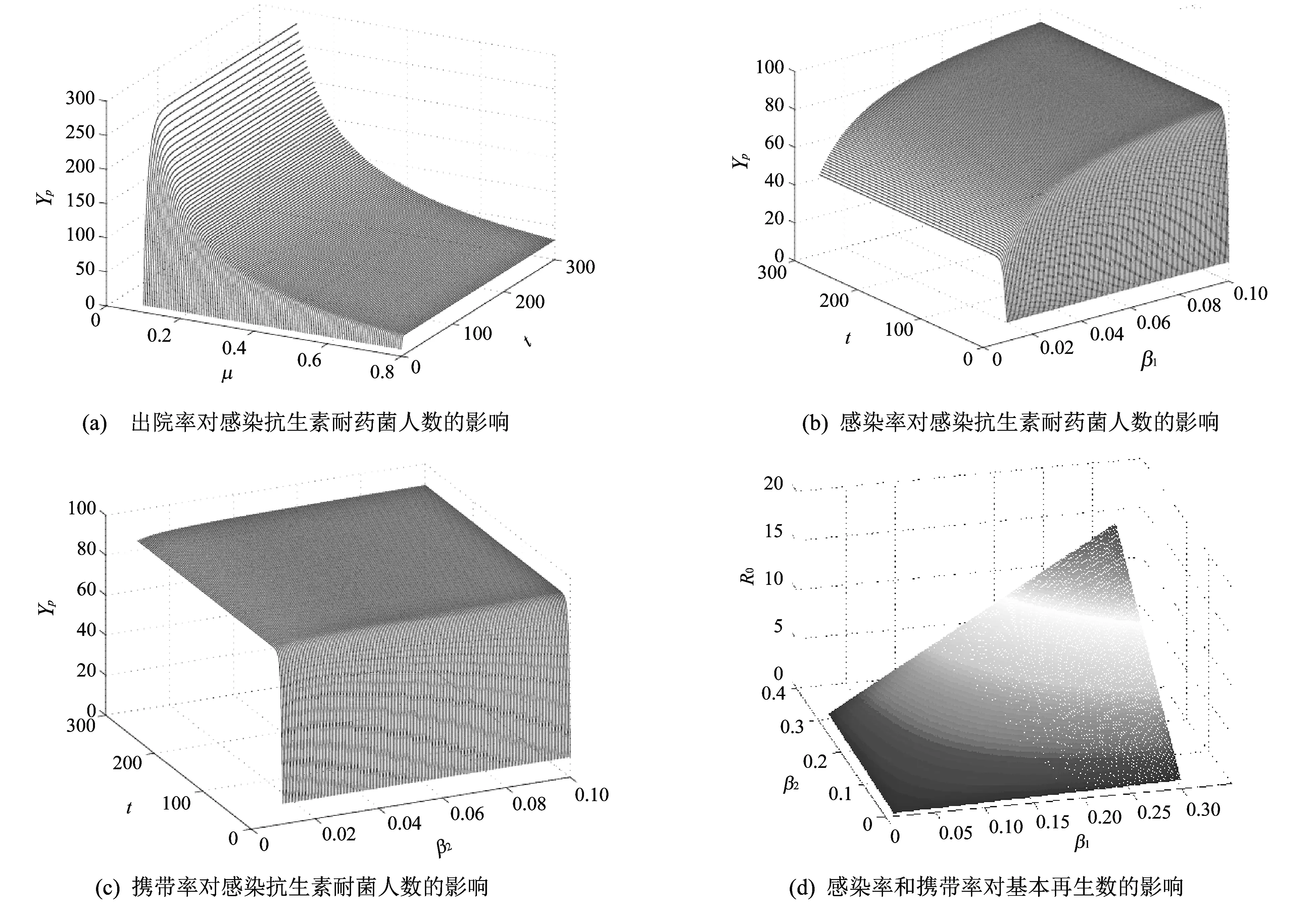
图 3 部分参数的敏感性分析图Fig.3 The figure of part parameter sensitivity analysis

4 结 论

通过泛函微分方程组的稳定性分析及MATLAB数值模拟验证， 本文得出当R0<1时， 该模型的无病平衡点是全局渐近稳定的； 当R0>1时， 该模型的地方病平衡点存在且唯一， 且全局渐近稳定. 可见在这类院内抗生素耐药菌传播模型中， 感染期时滞的存在并不影响整个模型的稳定性. 但是从数值模拟结果中可以看出， 感染期时滞的长短会影响抗生素耐药菌传播峰值出现的时间. 高出院率也有助于控制疾病传播. 因此在医疗条件有限的情况下， 即使不能把出院率保持在一个很高的水平， 也一定要重视出院率的提高， 合理缩短患者住院时间， 住院治疗与回家疗养相结合. 坚持按照病情将住院区划分的原则， 减少病人流动. 即使医护人员对病菌的携带率再低， 对整个疾病的爆发影响都很大， 因此医护人员要高度重视落实消毒、 更换衣物、 减少医护人员跨诊室调动等降低携带率的措施， 以便控制抗生素耐药菌在院内的传播.

[1]马成云, 李波, 李文君, 等. 医院感染的预防和控制[J]. 中华医院感染学杂志, 2005, 15(5)： 550-552. Ma Chengyun, Li Bo, Li Wenjun, et al. Prevention and control of hospital infection [J]. Chinese Journal of Hospital Infection, 2005, 15(5)： 550-552. (in Chinese)

[2]王醒, 蒋华, 吕海, 等. 院内感染控制现状及若干新技术途径[J]. 东南大学学报(医院版), 2013, 32(3)： 361-363. Wang Xing, Jiang Hua, Lü Hai, et al. The nosocomial infection control present situation and some new technology way [J]. Journal of Southeast University (Hospital), 2013, 32(3)： 361-363.(in Chinese)

[3]Spicknall I H, Foxman B, Marrs C F, et al. A modeling framework for the evolution and spread of antibiotic resistance： literature review and model categorization[J]. American Journal of Epidemiology, 2013, 178(4)： 508-520.

[4]Pei R. Revised model for antibiotic resistance in a Hospital[D]. Johnson City: East Tennessee State University, 2015.

[5]Webb G F, D'Agata E M C, Magal P, et al. A model of antibiotic-resistant bacterial epidemics in hospitals[J]. Proceedings of the National Academy of Sciences of the United States of America, 2005, 102(37)： 13343-13348.

[6]D’Agata E M C, Magal P, Olivier D, et al. Modeling antibiotic resistance in hospitals： the impact of minimizing treatment duration[J]. Journal of Theoretical Biology, 2007, 249(3)： 487-499.

[7] Bonhoeffer S, Lipsitch M, Levin B R. Evaluating treatment protocols to prevent antibiotic resistance[J]. Proceedings of the National Academy of Sciences of the United States of America, 1997, 94(22): 12106-12111.

[8]Sun H R, Lu X, Ruan S. Qualitative analysis of models with different treatment protocols to prevent antibiotic resistance[J]. Mathematical Biosciences, 2010, 227(1)： 56-67

[9]Wei H M, Li X Z, Martcheva M. An epidemic model of a vector-borne disease with direct transmission and time delay[J]. Journal of Mathematical Analysis and Applications, 2008, 342(2)： 895-908.

[10]李甜甜. 几类带有时滞的传染病模型稳定性分析[D]. 太原： 中北大学, 2014.

[11]Xue Y K, Li T Y. Stability and Hopf bifurcation for a delayed SIR epidemic model with logistic growth[J]. Abstract and Applied Analysis, 2013(4): 764-787.

[12]Xue Y K, Wang X Q. Stability and local hopf bifurcation for a predator-prey model with delay[J]. Discrete Dynamics in Nature and Society, 2012(2): 742-766.

[13]Xu R. Global dynamics of an SEIS epidemiological model with time delay describing a latent period[J]. Mathematics and Computers in Simulation, 2012, 85： 90-102.

[14]马佳辉, 薛亚奎. 医院内抗生素耐药性传染的稳定性与 Hopf 分支[J].中北大学学报(自然科学版), 2015, 36(3)： 261-267. Ma Jiahui, Xue Yakui. Stability and Hopf branch of antibiotic resistance in hospital infection[J]. Journal of North University (Natural Science Edition), 2015, 36(3)： 261-267. (in Chinese)

An Antibiotic Resistance Epidemic Model with the Time Delay and the Stability Analysis of the Model

FENG Dan-dan, XUE Ya-kui

(School of Science, North Universtiy of China, Taiyuan 030051, China)

In view of the influence of nosocomial infection on antibiotic resistant bacteria spread, combined with the characteristics of nosocomial infection and considering the direct communication between doctors and patients and the indirect spread of antibiotic resistant bacteria among patients, a type of infectious disease model with infection delay was set up. Anantibiotic resistance model in hospitals with delay was investigated. The probability of infected-patients was still in the hospital after the moment ofτhas been considered. A basic reproduction number which determines the outbreak of infectious disease was found. Through using Routh-Hurwitz criterion and Lasalle-Liapunov invariant set principle obtained that ifR0<1 the disease-free equilibrium was locally and globally asymptotically stable for anyτ≠0; ifR0>1, the endemic equilibriums of the model was exist and unique, it was locally and globally asymptotically stable for anyτ≠0. The time delayτhas no effect on the stability of the equilibria. Finally, a series of numerical simulations are presented to illustrate the mathematical findings.

delay model; antibiotic resistance; medium of health care workers; time of infection

2016-08-31

国家自然科学基金资助项目(11301491)； 山西省自然科学基金资助项目(2015011009)

冯丹丹(1990-)， 女， 硕士生， 主要从事生物数学的研究.

薛亚奎(1970-)， 男， 教授， 博士， 主要从事生物数学的研究.

1673-3193(2017)02-0103-07

O29

A

10.3969/j.issn.1673-3193.2017.02.002