邻域嵌入的张量学习*
2017-07-31李凡长
路 梅,李凡长
1.苏州大学 计算机学院,江苏 苏州 215006
2.江苏师范大学 计算机学院,江苏 徐州 221116
邻域嵌入的张量学习*
路 梅1,2,李凡长1+
1.苏州大学 计算机学院,江苏 苏州 215006
2.江苏师范大学 计算机学院,江苏 徐州 221116
+Corresponding author:E-mail:lfzh@suda.edu.cn
LU M ei,LI Fanzhang.Neighborhood-embedded tensor learning.Journal of Frontiers of Computer Science and Technology,2017,11(7):1102-1113.
传统的机器学习算法把数据表示成向量的形式进行处理,而现实世界许多应用中的数据都是以张量形式存在的,如图像、视频数据等,如果将这些本质上非向量形式的数据强制转换成向量表示,不仅会产生维数灾难和和小样本问题,而且会破坏数据本身的内部空间排列结构,不利于发现数据的好的低维表示。判别邻域嵌入(discrim inant neighborhood embedding,DNE)是比较流行的面向向量的判别分析方法,在改进DNE算法的基础上,提出了面向张量数据的局部一致保持的邻域嵌入张量判别学习(neighborhood-embedded tensor learning,NTL)算法。NTL算法不仅克服了DNE面向向量的缺点,而且弥补了DNE方法偏重数据的邻域点而忽略数据的非邻域点影响的不足,通过精心设计目标函数(嵌入3个图:同类结点的邻接图、不同类结点的邻接图、其他结点的关联图),使投影空间的同类结点更加紧凑,不同类结点更加疏远,从而增强了算法的判别能力。3个公开数据库(ORL、PIE和COIL20)上的实验验证了NTL拥有更高的识别率,同时也拥有更高的算法效率。
判别邻域嵌入(DNE);张量子空间分析(TSA);维数约简;判别分析;张量学习
1 引言
随着科学技术的飞速发展,越来越多的应用研究需要处理大量的高维数据,如图像检索、文本分类、语音识别和基因表示等。为了有效地表示和识别高维数据,传统的机器学习算法[1-16]把原始的高维数据投影到低维向量空间进行降维和特征提取,最大限度地保留其内在信息的同时得到高维数据的低维表示。维数约简对于处理高维数据非常重要。目前较为流行的降维算法有主成分分析(principal componentanalysis,PCA)[7,12]、半监督降维方法(sem isupervised dimensionality reduction,SSDR)[13,17]、边界Fisher分析(marginal Fisher analysis,MFA)[13]、局部保持投影(locality preserving projections,LPP)[10]、判别邻域嵌入(discriminantneighborhood embedding,DNE)[14]等。PCA方法广泛应用于图像检索和特征提取中,是经典的降维方法。PCA通过最大化代表原始图像的协方差矩阵,以达到最小化重建样本误差,最大限度保留数据的全局结构信息的目的。PCA方法是一种无监督的方法,只能解释两个特征集合之间的全局相关关系,而且只能作用于向量表示的数据。为了得到数据更合理的低维表示,降维过程中充分利用有标记信息以及保留样本点的判别信息和局部结构信息非常重要。SSDR是一种半监督的降维方法,能够充分利用有监督信息和无类别标记信息降维。MFA方法考虑到样本数据的判别信息,构建类内邻接图和边界点的类间邻接图,通过最小化类内距离之和与类间距离之和的比值寻找最优投影方向。LPP方法是拉普拉斯映射的一种线性近似,同时具有流形学习方法和线性降维方法的一些优点,但是LPP方法是无监督学习方法,没有有效地利用已知训练点的分类信息。
与PCA方法类似,SSDR、MFA、LPP和DNE方法也都是面向向量的降维方法。但是现实世界的许多应用中,数据都表示成张量形式。例如,图像可以表示成二阶张量,视频可以表示成三阶张量。如果将这些本质上非向量形式的数据强制转换成向量表示,会产生维数灾难和小样本问题。具体来说,将矩阵或者更高阶的数据表示成一阶向量,形成了高维的向量空间,面向向量的降维方法在求解投影向量时需计算解特征值问题,计算过程由于维数太高过于耗时,从而产生维数灾难。同时,样本数目常常小于向量空间的维数,因此需求解特征值的矩阵奇异。为解决此类问题,面向向量的降维方法通常先用PCA降维,但是这一过程常常会丢失某些有用的判别信息。除此之外,基于向量的表示破坏了图像、视频等多维数据本身的内部空间排列结构,在寻找投影向量的过程中不考虑数据本身在空间排列上的约束,因此不利于发现数据的低维表示。为了克服上述缺点,在传统机器学习算法的基础上延伸了许多面向张量的学习算法[18-24]。基于张量的降维方法可以直接处理张量数据,避免了直接处理向量所带来的一系列问题。He等人提出的张量子空间分析(tensor subspace analysis,TSA)方法可以看成是LPP算法在张量上的拓展[20]。
本文对DNE方法进行改进,并和张量表示结合,提出了一种新的算法——领域嵌入的张量判别学习(neighborhood-embedded tensor learning,NTL)方法。在DNE中,大小为n1×n2的图像表示成向量空间数据点,DNE的线性转换表示为Y=PTX,其中P是n×n的投影矩阵,因此DNE有n个待估计的参数。在本文方法中,图像表示成二阶张量,张量子空间的线性转换为Y=UTXV,其中U和V分别是大小为n1×d1(d1<n1)和 n2×d2(d2<n2)的矩阵,共有 2(d1+d2)个待估计的参数,远远小于DNE算法需要估计的参数。NTL方法通过构造3个图(同类结点的邻接图、不同类结点的邻接图、其他结点的关联图),精心设计目标函数,通过最小化目标函数使得同类结点更加紧凑,不同类结点更加疏远。
NTL方法在以下几方面值得关注:
(1)传统的机器学习方法如PCA、MFA、DNE等方法都是面向向量的维数约简算法,都是通过找到一个从高维到低维的映射实现降维。NTL方法通过寻找映射l2<n2)实现降维。
(2)NTL方法的计算比较简单,通过计算两个特征值问题即可。因为求解特征值的矩阵大小为n1×n1以及n2×n2,远远小于面向向量算法的求解特征值的矩阵大小,所以NTL的存储空间和时间复杂度相对较小。
(3)NTL方法不仅关注了结点的相邻关系对低维空间数据点关系的影响,同时也考虑了结点的不相邻关系对低维空间数据点关系的影响,因此和DNE相比具有更强的判别性能。
(4)本文主要考虑二阶张量的学习问题,NTL方法也可以推广到更高阶的张量学习中。
本文组织结构如下:第2章是张量和DNE方法的相关知识的简单介绍;第3章提出邻域嵌入的张量学习方法,给出目标函数和优化算法;第4章通过若干个分类方法的对比实验,验证本文方法的有效性;第5章是总结和展望。
2 相关知识介绍
2.1 张量
2.1.1 张量代数
定义1(N阶张量)被称为p阶逆变、q阶协变的N阶张量,若在坐标变换时,其分量按如下方式变换:
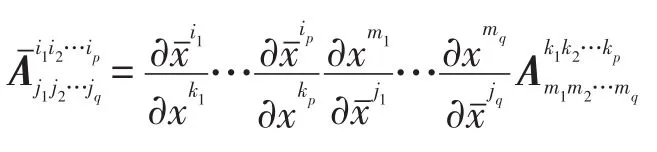
其中,N=p+q。
张量A的每一维称作一个模式(mode),高阶张量又称多模态数据、多重线性代数。如,N阶张量共有N个模式,维I1,I2,…,IN分别叫作第一模式,第二模式,…,第N模式。
人们熟知的标量是零阶张量,向量是一阶张量,矩阵是二阶张量。
定义2(张量的n-mode展开)张量的模式 n 展开为,其元素的行坐标为 in,列坐标为 (in+1-1)In+2In+3…INI1I2…In-1+(in+2-1)In+3In+4…INI1I2…In-1+(iN-1)I1I2…In-1+(i1-1)I2I3…In-1+(i2-1)I3I4…In-1+ …+in-1。
张量的n-mode展开实质上是把高阶张量展开成矩阵集合的形式,又叫张量矩阵化。
例如,三阶张量按第一模式有两种展开方式,如图1所示。
定义 3(张量乘法) 设是n-阶张量,是矩阵,则张量A和矩阵U的乘积是一个 I1×I2×…×In-1×J×A×In+1×…×IN张量,又叫nmode积,表示如下:

张量乘法用张量展开式表示如下:

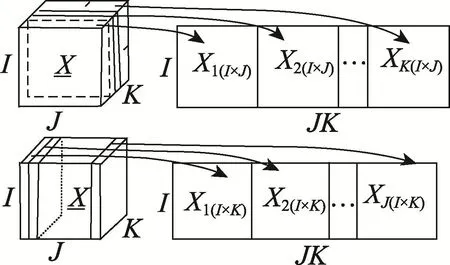
Fig.1 Two kindsof three-order tensorunfolding图1 三阶张量按照第一模式展开的两种方式
2.1.2 张量学习过程
图2给出了数据的张量表示的机器学习过程。由若干个张量表示的训练样本组成训练样本集合,使用张量学习方法,如TSA等,把训练样本TS投影到由基向量U(1)×U(2)×…×U(N)张成的空间,得到训练样例的低维表示GS,然后利用基向量U(1),U(2),…,U(N)把张量表示的测试样例TT投影到基向量张成的空间得到测试样例的低维表示GT,最后可以使用KNN、SVM等方法实现分类、检索等应用。
2.2 DNE算法
DNE算法是有监督子空间学习方法。利用邻域信息和类别信息,DNE算法使得数据样本在低维空间的投影保持了原来的邻域关系,同类样本的低维投影形成紧凑的子流形,不同类的样本投影尽可能地分开。
印刷行业的生产过程中,难免会由于溶剂型油墨的挥发而产生VOCs,因洗车水、润版液、清洗橡皮布等产生废液,从而对环境产生影响。当问及多家企业对于政府下达的如此严苛的环保政策的看法时,回答多是:企业的立场应与政府保持一致,如此严苛的环保要求一定程度上对企业来说是一种约束与鞭策,它能更好地促进企业规范化、可持续化、绿色化发展。客观上也解决了印刷行业供给侧改革问题,即要求清理僵尸企业,淘汰落后产能,将企业的发展方向锁定为新兴领域、创新领域,创造新的经济增长点。在严峻的政策环境下,只以价格取胜而不顾及质量、环保要求的企业被关闭,印刷市场更加规范,客观上增加了符合要求企业的活源。
DNE算法的目标函数如下所示,

其中,I是单位矩阵;P是投影矩阵。

3 邻域嵌入的张量学习
3.1 邻域嵌入的张量学习方法及目标函数是二阶张量,li∈{1,2,…,c}是Xi的类别标记,N是样本的个数,n1和n2分别是Xi的第一模式和第二模式的维数,c是
DNE方法是一种有监督的学习方法,面向的是向量形式的数据。如果要处理的数据是图像,则使用DNE方法分类时,首先要把图像数据转换成向量,然后才能使用DNE方法进行处理。许多已有的降维方法都是以这种方式处理图像数据的,但是文献[25]指出这样的处理方式对图像数据而言并不是十分有效。本文提出一种新颖的面向张量数据的子空间学习方法,叫作邻域嵌入的张量学习方法NTL。NTL方法可以看作是对DNE方法改进,并将其拓展到张量空间的学习上。
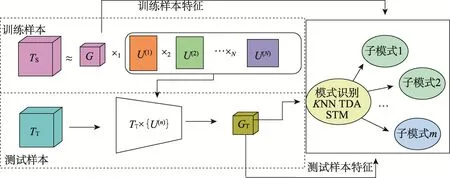
Fig.2 Tensor-data-basedmachine learning process图2 数据张量表示的机器学习过程
NTL方法描述如下:依据给定的数据集和类别标记,对DNE稍作改进。把所有的结点分成3类,第一类是同类的k近邻结点,第二类是不同类的k近邻结点,第三类是除了第一类、第二类以外的其他结点。对于第一类结点,通过降维以后,希望这些结点更加紧凑;对于第二类结点,希望降维后的结点更加疏远;对于第三类结点,根据这些结点的邻域链接情况,使用类似于PCA的方法确定其和邻域点的远近关系。由此,按照如下方式构造图G1、G2和G3。
G1=<V,E1,F1>:数据集上的所有数据构成图G1的顶点V={X1,X2,…,XN};若数据 Xi和 Xj属于同一类,并且 Xi是 Xj的 k1-邻近点,或者 Xj是 Xi的 k1-邻近点,则在结点Xi和Xj之间连一条线;若数据Xi和Xj不属于同一类,并且Xi是Xj的k2-邻近点,或者Xj是Xi的k2-邻近点,则在结点Xi和Xj之间连一条线.图G1的权重F1可以按如下方式定义:

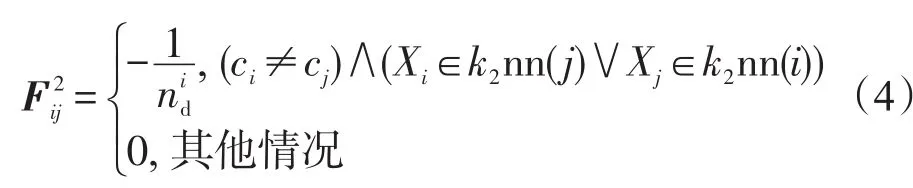
G3=<V,E3,F3>:数据集上的所有数据构成图G3的顶点V={X1,X2,…,XN};若数据 Xi和 Xj属于同一类,并且 Xi不是 Xj的k1-邻近点,或者 Xj不是 Xi的k1-邻近点,则在结点Xi和Xj之间连一条线;若数据Xi和 Xj不属于同一类,并且 Xi不是 Xj的k2-邻近点,或者Xj不是Xi的k2-邻近点,则在结点Xi和 Xj之间连一条线。图G3的权重F3按如下方式定义:
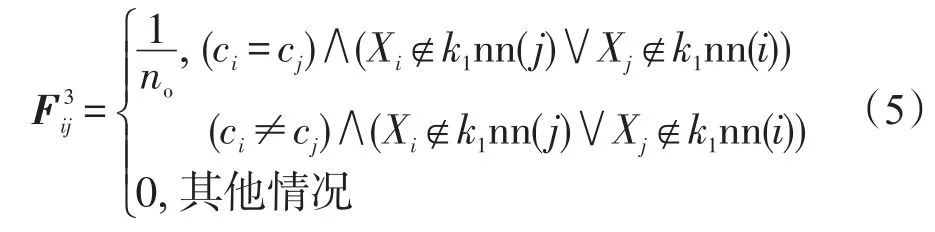
其中,no=N2-ns-nd。
投影后的类内紧凑程度为:

投影后的类间分离程度为:

同时,希望投影后第三类结点均方差尽可能大,则得到目标函数为:

3.2 目标函数的优化
先进行如下的化简:


3),“tr”表示矩阵的迹。又由于||A||2=tr(ATA),类似的,可以得到:

注意到上述两个函数的优化彼此相互依赖,因此U和V不能单独求解。为了求解上述优化问题,先固定矩阵V(满足条件VTV=Il1),则根据,可以计算出和的值,带入优化公式(1)。优化问题转化为求解的特征值问题。设d是的特征值的个数,不失一般性,设特征值为λ1≥λ2≥…≥λd,其对应的特征向量分别为u1,u2,…,ud,取d1个最大的特征值对应的特质向量构成特征矩阵U。
4 实验结果
为了验证NTL算法的有效性,将其应用在3个公开数据库中,即ORL数据库(http://www.uk.research.att.com/facedatabase.htm l)、PIE数据库(http://mu.edu/projects/project_418.htm l)以及COIL20数据库(http://www.cs.columbia.edu/CAVE/software/softlib/coil-20.php),并与PCA、MFA、DNE、TSA等算法进行比较。每张图像数字化并归一化,其灰度值为0~255。为了有效地计算,所有图像都缩放为32×32像素。实验中,PCA、MFA和DNE算法处理的图像数据都表示成1 024维的向量形式,TSA和NTL算法处理的图像数据表示成(32×32)-维的二阶张量形式。为了避免小样本问题,MFA和DNE算法采用二次降维,另外由于PCA降维能去除噪声,为了测试在不去除噪声情况下算法的性能,采用随机降维,降到100维。设置NTL的参数α=20。随机选取训练集和测试集,利用计算得到的投影矩阵把训练集和测试集投影到低维空间,采用最近邻分类器进行分类,识别率为20次实验的平均值。实验中,设置TSA和NTL算法的迭代次数为2次。
4.1 ORL人脸数据库
ORL人脸数据库包含40人的400张人脸图像,每个人的图片总数为10张。其中一些人脸的图像是在不同时期拍摄的。人的脸部表情和脸部细节有着不同程度的变化,比如睁眼或闭眼、笑或非笑,以及戴眼镜或不戴眼镜;人脸姿态也有相当程度的变化,深度旋转和平面旋转可达20°。随机从每个个体集合中选取l(l=3,4,5,6,7,8),选择60%样本作为训练集,其余的40%作为测试集。
各算法在ORL数据集上的实验结果在表1、表2和图3中给出。表1给出了各算法作用在ORL数据集上的最好识别率,括号内的值是相应算法取得最好值时的判别子空间的维度。表2给出了各算法作用在ORL数据集上的最优识别结果(包括平均识别率及其对应的标准差)。图3给出了ORL数据集随机选取l=3和l=5时各算法随维度增加的识别率。

Table 1 Optimalaccuracy and cost time of allmethodson ORL database表1 ORL数据集上各算法最佳识别率和耗费时间

Table2 Averageaccuracy,mean varianceand optimalembedded dimension of allmethodson ORL database表2 ORL数据集上各算法平均识别率、均方差和最优嵌入维数

Fig.3 Accuracy ofallmethodsvs.dimension on ORL database图3 各算法在ORL数据集上随维度增加的识别率
从表1、表2以及图3中可以看到:
(1)对于ORL数据集上的每个l,NTL算法与原来的DNE算法相比,最佳算法识别率最高提升了24.7%(l=4),最低提升了6.9%(l=8),平均提升了12.3%。NTL算法的性能比PCA、MFA和DNE算法好,NTL算法略好于TSA算法。出现这种结果的主要原因是PCA、MFA和DNE算法都是面向向量表示形式的数据,NTL和TSA算法是面向张量表示形式的数据,因为张量表示的数据最大限度地保留了数据内在的结构,同时也克服了传统面向向量的算法存在的维数灾难、小样本等问题,所以与PCA、MFA和DNE算法相比,NTL算法和TSA算法能更好地保留数据的内在几何结构,获得数据更好的低维表示,从而取得较好的识别性能。
(2)从表1中可以看出,PCA算法耗费时间最少,NTL算法和TSA算法相当,但是比MFA和DNE算法耗费时间少。NTL算法不仅在识别率上而且在时间上都优于MFA和DNE算法。所有算法都运行在Intel Core i5-2520M 2.50 GHz,8 GB内存的个人电脑上,使用Matlab7.0编程实现。
(3)对于ORL数据集上的每个l,NTL算法的最好性能在较低维就能达到。在维数较低的时候,NTL算法的平均识别率随着张量子空间维数的增加迅速提升。当张量子空间的维数达到一定数值时,NTL算法的性能趋于平稳,提升幅度较小。
4.2CMUPIE人脸库
本文采用卡耐基梅隆大学的PIE人脸库,PIE是姿态(Pose)、光照(Illum ination)和表情(Expression)的缩写。CMU PIE人脸库建立于2000年11月,它来自68个人的40 000张照片,其中包括了每个人的13种姿态条件、43种光照条件和4种表情下的照片。随机从每个个体集合中选取l(l=5,10,20,30),选择60%样本作为训练集,其余的40%作为测试集。
各算法在PIE数据集上的实验结果在表3、表4和图4中给出。表3给出了各算法作用在PIE数据集上的最佳识别率和耗费时间。表4给出了各算法作用在PIE数据集上的最优识别结果(包括平均识别率及其对应的标准差),括号内的值是相应算法取得最好值时的判别子空间的维度。图4出了PIE数据集随机选取l=5和l=20时各算法随维度增加的识别率。

Table3 Optimalaccuracy and cost timeofallmethodson PIE database表3 PIE数据集上各算法最佳识别率和耗费时间

Table 4 Average accuracy,mean variance and optimalembedded dimension of allmethodson PIE database表4 PIE数据集上各算法平均识别率、均方差和最优嵌入维数

Fig.4 Accuracy of allmethodsvs.dimension on PIE database图4 各算法在PIE数据集上随维度增加的识别率
从表3、表4以及图4中可以看到:
(1)相对于上面的ORL数据库而言,PIE数据库较为复杂。当l值较小也就是训练样本较少时,PCA、DNE和MFA算法性能不是特别理想,随着l的增加,MFA算法性能有较大的提升。总的来说,对于PIE数据集上的每个l,NTL算法与原来的DNE算法相比,最佳算法识别率最高提升了62.6%(l=5),最低提升了31.9%(l=30),平均提升了51.3%。NTL算法的性能比PCA、MFA和DNE算法好,NTL算法略好于TSA算法。因为张量表示的数据最大限度地保留了数据内在的结构,同时面向张量表示数据的算法克服了维数灾难、小样本等问题,所以与面向向量表示数据的PCA、MFA和DNE算法相比,NTL和TSA算法能更好地保留数据的内在结构,获得数据更好的低维表示,从而取得较好的识别性能。
(2)从表3中可以看出,NTL算法耗费的时间远远小于传统的PCA、MFA和DNE算法,识别率却高于这些算法。NTL算法的耗费和TSA相当,识别率略高于TSA算法。和运行在ORL数据库的结果相比,NTL算法的时间耗费大大降低,原因可能是PIE数据库相对更大更复杂,NTL作为面向张量数据的算法,极大限度地关注数据内在的结构,在处理大数据上具有更强的能力。所有算法都运行在IntelCore i5-2520M 2.50 GHz,8 GB内存的个人电脑上,使用Matlab7.0编程实现。
(3)对于PIE数据集上的每个l,NTL算法的最好性能在较低维就能达到。在维数较低的时候,NTL算法的平均识别率随着张量子空间维数的增加迅速提升。当张量子空间的维数达到一定的数值时,NTL算法的性能趋于平稳,提升幅度较小。
4.3 各算法性能随着训练数据增加的变化情况
一个好的分类算法应当随着训练数据的增加,其分类精度也相应增加。本实验在哥伦比亚图像数据库COIL20上验证本文算法的有效性。哥伦比亚图像数据库包含20个对象,每个对象在水平上旋转360°,每隔5°拍摄一张照片,因此每个对象共72幅图,一共1 440幅图片。实验中按照5∶95,1∶9,2∶8,3∶7和4∶6的比例随机抽取训练样本集和测试样本集,实验进行20次,实验结果为其平均值。图5给出了训练样本和测试样本比例为5∶95,1∶9,2∶8以及3∶7时各算法随纬度增加的识别率。图6给出了各算法的最佳识别率随着训练样本和测试样本比率递增的实验结果。
从图5中可以看出,当训练样本数与测试样本数的比率较小时(如二者的比率为5∶95时),这些算法的性能有较大的差距。MFA算法的性能相对较差,其次是PCA和DNE算法,这3个算法都是面向向量的算法;然后是TSA算法,NTL算法性能最好,这两种算法都是面向张量的算法。这说明即使当训练样本数较少时,面向张量的算法因为保持着数据的内部几何结构性质,所以能在低维空间更好地表征原始数据。因此在训练样本数据较少时,张量表示的学习方法相对于传统的面向向量的学习方法在性能上更具有优势。随着训练样本数和测试样本数比率的提升(如二者的比率是3∶7时),这几种算法的性能几乎相当。从图6中可以看出,随着训练数据的增加,各算法的性能都得到了不同程度的提升。除此之外,还可以看出NTL算法的性能始终要优于PCA、MFA、DNE和TSA算法。
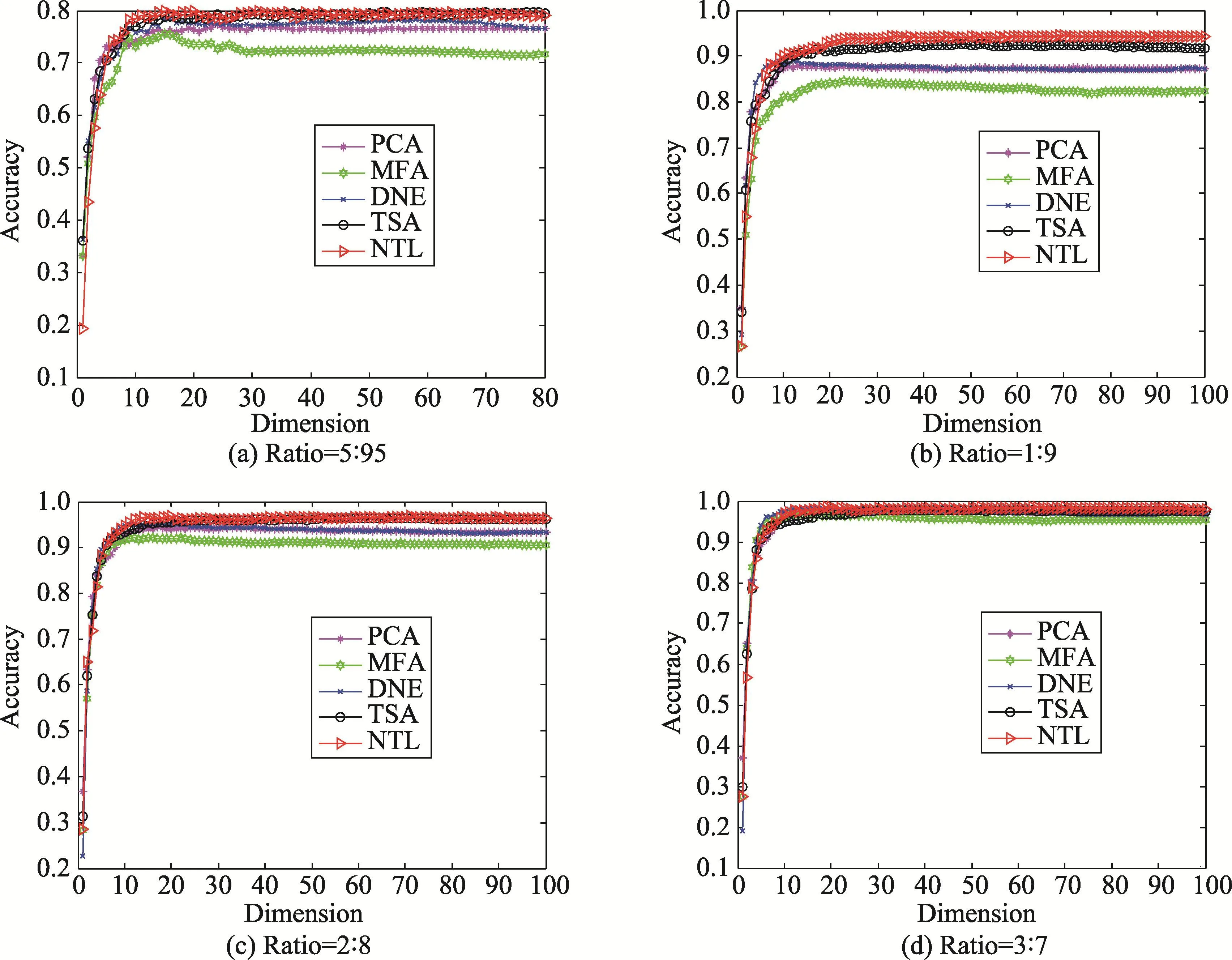
Fig.5 Accuracy of allmethodsvs.dimension on COIL20 database图5 各算法在COIL20数据集上识别率随维度增加的变化情况

Fig.6 Accuracy of allmethodsvs.ratio of training samplesand testing sampleson COIL20 database图6 各算法在COIL20数据集上识别率随训练样本和测试样本比率增加的变化情况
5 结论和展望
本文在改进的判别邻域嵌入(DNE)方法的基础上提出了新的面向张量数据的邻域嵌入的张量学习(NTL)方法。由于传统的机器学习算法把数据表示成向量的形式进行处理,现实世界以张量形式存在的诸多数据如图像、视频数据,如果被强制转换成向量表示,不仅会产生维数灾难和小样本问题,而且会破坏数据本身的内部空间排列结构,不利于发现数据好的低维表示。除此之外,DNE算法只是利用了数据之间的邻域关系,却忽略了非邻域关系对算法判别性能的影响。本文提出的NTL算法面向张量数据,解决了DNE算法存在的上述问题,通过实验也验证了NTL算法不仅提升了识别率,而且还提高了算法学习的效率,在处理更为复杂的数据上,NTL算法具有更强的能力。
[1]Batur A U,Hayes IIIM H.Linear subspaces for illumination robust face recognition[C]//Proceedings of the 2001 Conference on Computer Vision and Pattern Recognition,Kauai,USA,Dec 8-14,2001.Washington:IEEEComputer Society,2001:296-301.
[2]Belhumeur PN,Hespanha JP,Kriegman D J.Eigenfaces vs.fisherfaces:recognition using class specific linear projection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1997,19(7):711-720.
[3]Belkin M,NiyogiP.Laplacian eigenmaps and spectral techniques for embedding and clustering[C]//Proceedings of the 14th International Conference on Neural Information Processing Systems:Natural and Synthetic,Vancouver,Canada,Dec 3-8,2001.Cambridge,USA:M ITPress,2001:585-591.
[4]CaiDeng,He Xiaofei,Han Jiawei.SRDA:an efficientalgorithm for large-scale discrim inant analysis[J].IEEE Transactions on Know ledge and Data Engineering,2008,20(1):1-12.
[5]CaiDeng,He Xiaofei,Han Jiawei,etal.Orthogonal Laplacianfaces for face recognition[J].IEEETransactions on Image Processing,2006,15(11):3608-3814.
[6]He Ran,Zheng Weishi,Hu Baogang,et al.Nonnegative sparse coding for discriminative sem i-supervised learning[C]//Proceedings of the 2011 Conference on Computer Vision and Pattern Recognition,Colorado Springs,USA,Jun 20-25,2011.Washington:IEEEComputer Society,2011:2849-2856.
[7]Levin A,Shashua A.Principal component analysis over continuous subspaces and intersection of half-spaces[C]//LNCS 2352:Proceedings of the 7th European Conference on Computer Vision,Copenhagen,May 28-31,2002.Berlin,Heidelberg:Springer,2002:635-650.
[8]Li Ping,Bu Jiajun,Yang Yi,etal.Discriminative orthogonal nonnegative matrix factorization w ith flexibility for data representation[J].Expert Systems w ith Applications,2014,41(4):1283-1293.
[9]LiWei,Prasad S,Fow ler JE,et al.Locality-preserving dimensionality reduction and classification for hyperspectral image analysis[J].IEEE Transactions on Geoscience and Remote Sensing,2012,50(4):1185-1198.
[10]He Xiaofei,Niyogi P.Locality preserving projections[C]//Advances in Neural Information Processing Systems 16,Vancouver,Canada,Dec 8-13,2003.Cambridge,USA:MIT Press,2003:153-160.
[11]Shi Jun,Jiang Qikun,Zhang Qi,etal.Sparse kernelentropy componentanalysis for dimensionality reduction of biomedicaldata[J].Neurocomputing,2015,168(C):930-940.
[12]CaiDeng,He Xiaofei,Han Jiawei.Document clustering using locality preserving indexing[J].IEEE Transactions on Know ledgeand Data Engineering,2005,17(12):1624-1637.
[13]Yan Shuicheng,Xu Dong,Zhang Benyu,et al.Graph embedding and extension:a general framework for dimensionality reduction[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(1):40-51.
[14]Zhang Wei,Xue Xiangyang,Lu Hong,et al.Discrim inant neighborhood embedding for classification[J].Pattern Recognition,2006,39(11):2240-2243.
[15]Lu Mei,Zhao Xiangjun,Zhang Li,et al.Sem i-supervised concept factorization for document clustering[J].Information Sciences:an International Journal,2016,331(C):86-98.
[16]Yang Xibei,Qian Yuhua,Yang Jingyu.Hierarchical structures on multigranulation spaces[J].Journal of Computer Scienceand Technology,2012,27(6):1169-1183.
[17]Zhang Daoqiang,Zhou Zhihua,Chen Songcan.Semi-supervised dimensionality reduction[C]//Proceedings of the 7th SIAM International Conference on Data M ining,M inneapolis,M innesota,USA,Apr 26-28,2007.Philadelphia,USA:SIAM,2007:629-634.
[18]De Lathauwer L,Vandewalle J.Dimensionality reduction in higher-order signalprocessing and rank-(R1,R2,…,RN)reduction inmultilinearalgebra[J].LinearA lgebra and ItsApplications,2004,391(1):31-55.
[19]Hall A,Qu G,Sethi IK,Hartrick C.Tensor-based temporal behavior analysis in pain medicine[C]//Proceedings of the 11th International Conference on Machine Learning and Applications,Florida,USA,Dec 12-15,2012.Washington:IEEEComputer Society,2012:626-629.
[20]He Xiaofei,Cai Deng,Niyogi P.Tensor subspace analysis[C]//Advances in Neural Information Processing Systems 18,Vancouver,Canada,Dec 5-8,2005.Cambridge,USA:M ITPress,2005:499-506.
[21]Ye Jieping,Janardan R,LiQi.Two-dimensional linear discrim inantanalysis[C]//Advances in Neural Information Processing Systems 17,Vancouver,Canada,Dec 13-18,2004.Cambridge,USA:M ITPress,2004:1569-1576.
[22]Sun Jiantao,Zeng Huajun,Liu Huan,etal.CubeSVD:a novel approach to personalized Web search[C]//Proceedings of the 14th InternationalConference onWorldWideWeb,Chiba,Japan,May 10-14,2005.New York:ACM,2005:382-390.
[23]ShashuaA,ZassR,Hazan T.Multi-way clustering using supersymmetric non-negative tensor factorization[C]//LNCS 3954:Proceedings of the 9th European Conference on Computer Vision,Graz,Austria,May 7-13,2006.Berlin,Heidelberg:Springer,2006:595-608.
[24]Ishteva M,De Lathauwer L,Absil P,et al.Dimensionality reduction for higher-order tensors:algorithms and applications[J].International Journal of Pure and Applied Mathematics,2008,42(3):337-343.
[25]Chen Songcan,Zhu Yulian,Zhang Daoqiang,et al.Feature extraction approaches based on matrix pattern:MatPCA and MatFLDA[J].Pattern Recognition Letters,2005,26(8):1157-1167.

LU Meiwas born in 1976.She isa Ph.D.candidate at Soochow University.Her research interests includemachine learning,pattern recognition and artificial intelligence,etc.
路梅(1976—),女,江苏徐州人,苏州大学计算机科学与技术学院博士研究生,主要研究领域为机器学习,模式识别,人工智能等。

李凡长(1964—),男,云南宣威人,1995年于中国科技大学获得硕士学位,现为苏州大学教授、博士生导师,主要研究领域为人工智能,机器学习等。
Neighborhood-Embedded Tensor Learning*
LUMei1,2,LIFanzhang1+
1.Collegeof Computer Science and Technology,Soochow University,Suzhou,Jiangsu 215006,China
2.College of Computer Science and Technology,Jiangsu NormalUniversity,Xuzhou,Jiangsu 221116,China
Mostof traditionalmachine learning algorithms process vectorized data,while in realworld a lotof data exist in the form of tensor,such as images and video.If these tensor data are forced to be vectorized,the so called“curse of dimensionality”and“small sample size problem”w ill be encountered as well as the intrinsic structure w illbe destroyed.Thus,thegood lower dimensional representation of theoriginaldata can notbe captured.Discriminant neighborhood embedding(DNE)is a popular discrim inant analysismethod but based on vectorized data.To address this issue,this paper proposes a novel neighborhood-embedded tensor learning(NTL)which inherits the power of DNE.In addition,NTL overcomes another lim itation of DNE that it neglects the role of the points out of the neighborhood of a data point.By designing an objective function elaborately(three graphs are encoded in the object function:intraclass graph,interclass graph and other points association graph),NTLmaps the data into a low dimension subspacewhere the data in the same classw illbemore compactand the data in the differentclassw illbe more separable.The experimental results on three public data bases(ORL,PIE and COIL20)demonstrate thatNTL achievesbetter recognition rate,whilebeingmuchmore efficient.
discrim inant neighborhood embedding(DNE);tensor subspace analysis(TSA);dimensionality reduc-tion;discrim inantanalysis;tensor learning
g was born in 1964.He
the M.S.degree in computer science and technology from University of Science and Technology of China in 1995.Now he is a professor and Ph.D.supervisor at Soochow University.His research interests include artificial intelligence andmachine learning,etc.
A
:TP181
*The NationalNatural Science Foundation of ChinaunderGrantNos.61033013,61402207,61272297(国家自然科学基金).
Received 2016-05,Accepted 2016-07.
CNKI网络优先出版:2016-07-14,http://www.cnki.net/kcms/detail/11.5602.TP.20160714.1616.004.htm l
