面向可视化的全局自适应等距映射算法*
2017-07-31王曦杨程春玲陈兴国
王曦杨,程春玲,陈兴国
南京邮电大学 计算机学院,南京 210003
面向可视化的全局自适应等距映射算法*
王曦杨,程春玲+,陈兴国
南京邮电大学 计算机学院,南京 210003
+Corresponding author:E-mail:chengcl@njupt.edu.cn
WANG Xiyang,CHENG Chunling,CHEN Xingguo.Globaladaptive isometricmapping algorithm for visualization.Journalof Frontiersof Computer Scienceand Technology,2017,11(7):1092-1101.
等距映射;数据可视化;拓扑稳定;数据流形
1 引言
在数据的可视查询与分析过程中,不可避免地会遇到大量高维的数据,如全球气候数据、基因分布数据、金融交易数据等,若直接对原始数据进行处理,很难保证数据可视化的质量以及响应速度[1],迫切需要合适的数据约简技术,提取有效而又合理的特征数据并用于可视化应用中。近几年,美国俄亥俄大学以及斯坦福和华盛顿大学成立的交互式数据实验室(Interactive Data Lab)在这方面的研究取得了较大进展,其面向数据可视化的约简技术包括过滤采样[1](filtering&sampling)、数据聚合[2](data aggregation)和混合约简[3](hybrid reduction)3种方式。然而这些方法针对特定数据和实际系统需求而设计,虽对特定数据有很好的处理效果,但通用性并不理想。相比之下,数据的降维映射作为一种传统的底层的数据约简策略,具有较高的普适性,可为数据可视化提供很好的技术支持,非常具有研究意义。
降维映射的目标就是将对象数据映射到一个二维或者三维空间,并且保留尽可能多的数据间的本质结构[4]。代表方法有保留局部特征的局部线性嵌入(locally linearembedding,LLE)[5]、拉普拉斯特征映射[6](Laplacian eigenmaps,LE)和局部切空间排列[6](local tangentspace alignment,LTSA);保留全局特征的多维尺度变换[4](multidimensionalscaling,MDS)和等距映射[7](isometricmapping,Isomap)。仅保留局部特征的方法具有更快的运算速度,但映射后难以保证数据对象之间的测度,从而对数据结构及其内在规律的分析造成负面影响。MDS在数据可视化方面已有广泛的应用,但它并不能对非线性分布的数据进行降维。作为MDS的有效扩展,基于数据流形的Isomap算法[5]采用能有效表征数据全局几何结构的近邻图和测地距离对数据进行降维可视化处理,考虑到了较大规模、非线性数据结构的整体性。然而,Isomap算法极大依赖于难以有效选取的邻域大小,极易造成数据拓扑不稳定的情况[6];另外,Isomap算法的复杂度非常高,实际计算量很大[6]。在高度交互式的可视化实际应用背景下,很难满足交互实时性和可视化准确性的需求,极大限制了该类算法的实际应用。
针对以上两个问题,本文总结了现有改进方法的优劣,基于Isomap的核心思想,提出了具有全局自适应性的GA-Isomap(globaladaptive-Isomap)算法。主要工作在于:(1)引入数据区域密度作为唯一评估指标,提出数据区域密度的衡量方式和区域划分方式;(2)基于区域密度和数据点连通性,提出渐进式的邻域构建方法和基于区域的地标选取方法;(3)提出基于双层图的降维映射策略,利用邻域图和仅由地标构造出的框架图提高映射准确性;(4)通过实验将本文算法与现有算法进行比较分析。
2 相关工作
Isomap算法采用图模型思想,通过捕捉原始数据集的内在流形结构,获得观测数据集在低维空间的相应描述[7]。目前对Isomap的研究主要包括邻域图构建方法、路径计算方法和快速降维映射三方面,可从拓扑稳定性和算法效率两方面展开。
为提高Isomap方法的拓扑稳定性,主要采用基于映射质量反馈的方法、删除短路边的方法以及动态邻域构建方法。
基于结果反馈的方法就是对运行结果进行评估,从而进行相应优化策略。典型的有基于“残差”的评估优化方法[8],利用目标残差和实际残差的差值来递增或递减地调整近邻值;还有Agarwal等人提出的PLACECENTER[9]以及Choi等人提出的ParallelGTM(generative topographicmapping)[10]优化框架,根据映射结果的误差来调整矩阵的分解方式。这类方法为了将误差值控制在一个较小阈值当中,需不断迭代处理先前的结果,很难控制运行时间。
删除“短路”边的方法可避免数据流形上本不相邻的两数据点相连,因而可有效保证邻域图的准确性和拓扑稳定性。孟德宇等人提出流形重构法[11],利用流形空间与低维表示空间之间的显式映射关系矩阵,将原有点对点的映射扩展至局部空间到空间的快速映射。邵超等人提出的P-Isomap算法[12],通过分配权重值抑制由邻域大小不合适而产生的“短路”边对距离保持的影响。Gao等人提出judgeShortCircuits算法[13],根据“短路”边途经低密度区域的特点,利用基于高斯核函数的核密度估计法,取一条边上的3个四分位点的平均局部密度来近似区域密度,以此鉴别并删除邻域图中可能的“短路”边。然而,这类方法只是在原有算法的基础上简单增加了判断和删除的步骤,不可避免地增加了计算量,且依旧受静态参数的影响。
动态邻域构建方法使得近邻图的构建摆脱了静态参数的限制,降低了算法敏感度。Zhan等人提出Isomap w ith dynam ic neighbor[14],基于切空间向量评估数据点分布情况和距离远近,动态选取近邻。此外,Mekuz[15]、Gao[16]等人也提出类似方法,只是数据点向切空间的投影方式以及评估指标稍有不同。Yang提出利用最小代价生成树和贪心算法的思想来构建邻域图[17],可保证邻域图的准确性和连通性。İnkaya等人提出了Isomap w ith NC算法[18],使用加布里埃尔图(Gabriel graph)来计算数据点的区域连通性和近似关系,从而为每个数据点分配特定的近邻。然而,基于切空间的评估法对数据有较高要求,其内部参数必须在有足够的采样数据、相对恒定的曲率和相对均匀的分布密度前提下才可计算得到。利用最小代价生成树和使用加布里埃尔图的方法,其中临界节点的判断逻辑增加了算法复杂度。为提高算法运算速度,目前主要是设计快速映射方法,主要措施有基于地标的映射方法和基于约简距离矩阵的映射方法。地标的概念以及经典的L-Isomap算法[19]由Isomap创始人Tenenbaum提出,通过固定地标,仅计算每个数据点与地标点的距离,从而减少距离矩阵的计算量,但仍面临拓扑稳定性的问题。为此,Orsenigo提出L-IsomapSC算法[20],引入“亲密度”和“类同性质”两个新指标来确定地标点集的权重,最终找出能够覆盖所有数据点的地标点集合。其结果虽然提高了数据拓扑稳定性,但寻找最大权重点集增加了较大的时间开销,且其地标所占比仍需人为控制。
基于约简距离矩阵的映射是相对新颖的优化方法,代表性的有Dzw inel等人提出的快速nr-MDS算法[21],对距离矩阵进行奇异值分解,利用约简的相异矩阵进行运算,使得映射过程的空间复杂度仅为线性。还有Yang等人提出的MMD-Isomap(multi-manifold discrim inant Isomap)算法[22],基于不同的数据流形区域,对原始数据的距离矩阵进行分割,再分别对每个矩阵进行降维映射计算。该类方法虽降低了计算复杂度,但其映射结果并不稳定,会出现数据“拥挤”现象,即多个数据点重叠。
3 GA-Isomap算法设计
理想的等距映射方法应摆脱邻域半径、近邻值、地标所占比等静态参数影响,提高拓扑稳定性的同时尽量减少时间开销。若算法能主动适应原始数据的分布特征,则可以摆脱静态参数的人为设置,更加准确有效地抓取原始数据流形,进而确定每个数据点的近邻,构建邻域图。此时,如果可以采用一个简单且实用的评估指标,统筹考虑近邻和地标的选择,将大大简化处理流程。数据密度作为一个典型特征,可直观反映原始数据之间的关系,因此本文将原始数据区域密度作为唯一指标,以此判断出每个数据点的近邻,划分其所处区域,完成邻域图的构建,并根据区域选择出地标。在最终映射计算时,由于这里的地标是根据区域选取的,可利用地标点之间构成的完全连通图作为后续数据点的映射框架,设计基于双层图的映射,尽量确保数据点之间的相对位置关系,也遵循等距映射方式最基本的目标。
3.1 原始数据区域划分
通过数据的分布密度可以直观量化出原始数据的分布情况,从而为每个数据点的近邻选择和区域地标点选择提供参考依据。但由于高维空间的区域大小不易确定,且这里只需对数据分布区域进行区分,根据数据流形中的局部线性特征[5],可统一用线密度作为一个衡量指标。为简化计算,本文引入核心近邻和密度近邻的概念。文献[17]同样提到这样的概念,但只是通过连接距离的远近进行简单区分,对其定义并不明确,为使得后续邻域图尽量只包含短边以便遵循数据流形,这里对其进行重新定义。
定义1(核心近邻)原始数据构成的连通图中,与数据点xi直接相连的点即为点xi的核心近邻。
定义2(密度近邻)原始空间中,与数据点xi处于同一密度区域的数据点即为点xi的密度近邻。
定义3(区域密度)数据点xi所处区域的密度值为其对应密度近邻集合中数据点个数与相距最远的两点间距离的比值。
数据点xi的核心近邻构成核心近邻集合CNi,其密度近邻构成密度近邻集合DNi,通过构建密度近邻集合即可实现不同密度区域的划分。基于最小连通图,将未与点xi直接相连的点按欧式距离的非递减顺序排序,构成有序点集Pi;依次考虑Pi中的数据点Pi[j],加入DNi集合计算区域密度,即DNi={Pi[j]}⋃{xi}⋃CNi。令density()为数据集合的密度计算函数,任意两点 xm,xn∈DNi的欧式距离为 δmn,则密度计算公式可写为:

确定密度近邻的过程为:若密度值保持不变或是增加,则将该点看作数据点xi的近邻;若DNi的密度下降,则预示着一个不同密度区域的开始,将该点称为离点xi最近的区域断点,并从DNi中删除。
3.2 邻域图构建
现有的动态近邻构建法提供了很好的思路,但其构建完整图再删除边的做法造成了很多计算浪费。为提高构建的准确性和速度,本文的邻域图构建将基于区域划分的结果,采用逐步增加边的方法完成邻域图的构建,称之为渐进式构建法。可以说,近邻图的构建和区域的划分是同时进行的。
邻域图的构建将从最小连通图开始。最小连通图既能有效地避免“短路”边,也能较好地反映原始数据内在的流形结构,这也是该类算法能够成功运用的必要前提。只需利用k-nn方法从k=1开始递增式构建k近邻图,通过深度优先遍历判断图的连通性,即可得出最小连通邻域图G。
在构建过程中,每当确定一个数据点xi与其相应的密度近邻集合DNi后,增加边使得点xi与DNi中所有点直接相连,更新图G。如此构建将使得后续数据点判断密度近邻的计算量越来越少,因为对后续点,与其直接相连的数据点只会增多,即其初始集合CNi中的点数逐渐变多,由此可避免近邻点之间的重复判断。
3.3 地标点选取
随机选取地标点虽是最快的方法,但易造成数据点的丢失,难以保证完整的数据拓扑。为此,文献[21]提出当地标能够覆盖所有数据点时,可保证结果的准确性。这提供了一个很好的思路。由于本文方法在划分区域时充分考虑到了周围点的疏密分布,可以说一个密度区域中的点是相对紧凑的,因而选择该区域的中心点作为该区域的地标将非常具有代表性。相比于文献[21]所提出的基于类同性质和亲密度的权重覆盖判断方式,更容易理解和实现。
定义4(地标点)在密度近邻集合中,到其余所有点的平均距离最小的点,即是该密度区域的地标点。
令DNi集合中任意一点与其余点之间的平均距离函数为ad(),对任意点xj∈DNi,则该点到其余点的平均距离为:

那么该集合的地标点的选取公式可写为:
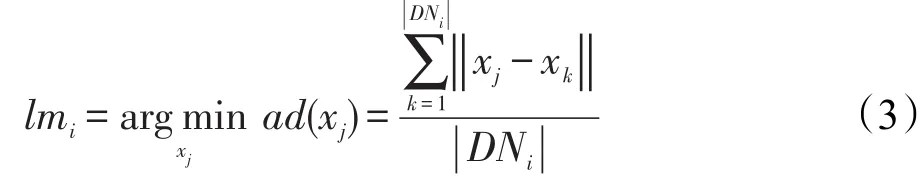
从DNi集合中求出集合中心点作为后续降维映射的地标,这意味着该地标点可代表邻域内的所有点,为避免不必要的选择冲突和数据点的重复判断,必须规定一个密度区域只允许出现一个地标点,其余点将不可能成为地标点。
3.4 基于双层图的降维映射
现有的方法往往只将地标作为一种减少计算量的手段,因而通常在降维映射后发生数据结构遭到破坏的情况,尤其在基于散点图的可视化应用中非常明显。若是利用地标点构成地标框架图GL,依此计算出地标测地距离矩阵DXGL,并将其映射结果作为数据点相对位置的参考,可使得后续数据点的映射更加准确。
此时,采用构建完全连通图的方式构建地标框图GL可极大提高地标测地距离矩阵DXGL的准确性。为尽量保证地标点之间的距离测度,最终基于MDS的映射目标函数可改进为:

其中,dXL(lmi,lmj)表示原始维度空间内地标lmi与lmj两点的测地距离,其值可通过矩阵DXGL获得;dYL(lmi′,lmj′)表示映射目标空间内与其对应的 lmi′与 lmj′两点的欧式距离,由此得出地标点在目标空间的映射坐标点集YL。
在地标映射完成后,只需通过邻域图G计算获得其余点与所有地标点的测地距离矩阵DXG,利用L-MDS[20]算法即可获得其余数据点的低维映射结果。
3.5 算法描述及复杂度分析
基于以上的设计方案和传统Isomap算法框架,可构造一个能够自适应构建邻域和地标的降维映射算法,称之为GA-Isomap算法。
算法GA-Isomap
输入:原始数据点集X={x1,x2,…,xn}
输出:目标空间对应点集Y={y1,y2,…,yn}
步骤1划分区域,构建邻域图

步骤2选取地标,构造地标完全图

步骤3基于双层图的降维映射

表1比较了GA-Isomap算法与传统Isomap[7]、LIsomap[20]、L-IsomapSC[21]和 Isomap w ith NC[18]算法的时间复杂度。
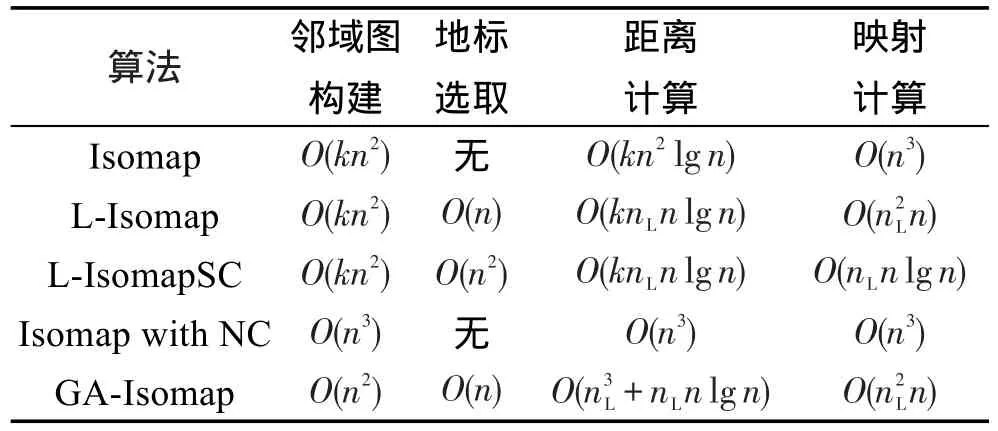
Table1 Complexity comparison of5 algorithms表1 5种算法的时间复杂度比较
不难发现,GA-Isomap在邻域图构建、地标选取和映射计算均达到目前较低的复杂度,且不受静态近邻值k和地标占比的影响。密度区域的划分大大简化了邻域构建和地标选取的过程,选取区域中心作为地标的方式使得新算法既具有传统L-Isomap的线性复杂度,也达到了L-IsomapSC所追求的地标全覆盖的目标。在路径计算方面,因为GA-Isomap为提高映射准确率,单独构建了完全图计算地标与地标的相对位置关系,不可避免地增加了计算复杂度。但在实际运行时,算法中的nL<<n,这将有效控制地标距离矩阵的规模和基于地标的映射计算量,实验结果也说明了本文方法的可行性。
4 实验结果与分析
本文采用函数生成无噪声干扰的sw iss roll标准测试数据集[6],其三维空间分布如图1(a)所示,数据呈卷状分布,其结果可反映出不同算法的流形捕捉性能。这里为更好地测试不同算法的拓扑稳定性,还采用changing-sw iss roll数据[23]进行测试,其三维空间分布如图1(b)所示。本文通过随机数生成器规定changing-sw iss roll局部子空间内的数据点个数,其整体依旧呈卷状分布,但该数据产生明显的疏密分布变化,其中对于数据点分布相对稀疏的局部子空间的映射结果更能切实反映出不同算法的拓扑稳定性。仿真环境为Matlab 2012b,硬件配置为Intel i5-3337u 1.8GHz CPU,8GB内存,操作系统为Windows7。部分测试代码来源于http://isomap.stanford.edu/。

Fig.1 Three-dimensionaldistribution of testdata图1 测试数据三维分布效果图
该实验首先使用2 000个数据点的sw iss roll和changing-sw iss roll数据测试各算法,通过直观的降维映射效果图反映各算法的拓扑稳定性;然后分别使用不同规模的测试数据,测试并比较各算法的运行时间。对比算法分别为 Isomap[6]、L-Isomap[20]、Isomap w ith dynam ic neighbor[14]和 Isomap w ith NC[18]。 由 于Isomap和L-Isomap的映射质量受静态参数影响,为选取较优结果进行比较,其近邻值k取常用的6、8,并将地标所占比设为文献[21]中的建议值0.5。Isomap w ith dynam ic neighbor和Isomap w ith NC算法均按照原文献进行初始参数设置,前者的最小近邻值设为4,后者的最小区域直径初始化为任意两点的最小距离。对于GA-Isomap算法,需将最小连通图构建部分中k-nn算法的k设为初始值1;将密度区域点集DNi最小长度设为2,避免产生空区域或单个孤立的数据点。
4.1 可视化映射效果
首先分别利用5种算法处理测试2 000点的sw iss roll和changing-sw iss roll数据,将其映射至二维平面内,绘制二维散点图。通过简单的颜色编码直观展示各算法对原始数据的邻域结构和整体拓扑结构的保留程度,处理结果如图2和图3所示,X轴表示水平方位,Y轴表示纵向方位。
从图 2(a)、(b)、(c)、(d)和图 3(a)、(b)、(c)、(d)可以看出,Isomap和L-Isomap的处理结果并不理想,数据内部和边缘都存在明显的畸变,对于changingsw iss roll则尤为明显,即使调整邻域参数k值也很难保证拓扑稳定,映射准确。如图2(c)、(d)红圈部分所示,部分区域出现严重空缺,固定近邻数、地标占比的方法导致映射结果具有很强的随机性。其余3个算法对于传统的测试数据均有非常好的映射效果,主要是因为传统sw iss roll的数据分布是相对均匀的。但是对于changing-sw iss roll测试数据,Isomap w ith dynam ic neighbor和Isomap w ith NC这两个算法在数据极为稀疏的区域都产生了严重的畸变,如图3(e)、(f)中红圈所示区域,并不能准确抓取离散区域的数据流形。
相比之下,GA-Isomap对不同分布状态的数据均有非常好的处理效果。因为该算法中的邻域构建充分考虑到了数据的区域特性,区域内的点彼此连通,使得测地距离的计算更加准确。另外,由于达到了地标全覆盖的目标,任意非地标的数据点都可以找到自己所在区域的地标,即使在数据极为稀疏的部分也能准确捕捉数据流形,并通过基于双层图的映射有效反映出原始数据的分布情况。
4.2 运行时间
对于两种数据的测试,每个算法均进行10次运算处理,取时间均值进行比较。时间开销的比较结果分别如图4、图5所示。
在测试数据规模较小(n≤1 500)时,各算法的运行时间差距并不大,但数据规模较大时,Isomap w ith dynam ic neighbor由于采用切空间的映射和评估来构建邻域图,过多的投影计算使其运行时间快速增长,时间开销相比原始Isomap并没有改善。Isomap w ith NC和L-Isomap对于算法运行时长的改善显著,但Isomap w ith NC需要重复判断并更新扩展近邻[18]、临界近邻[18]和最终近邻[18];L-Isomap 中固定地标百分比导致地标数呈线性增长,其计算时长增加也比较明显。另外,随机地标的策略导致其并不适合对小规模、稀疏分布的测试数据进行处理,会发生邻域图无法构建的情况,导致L-Isomap算法无法运行。因此对于changing-sw iss roll,本文未做1 500点以下的时间开销比较。
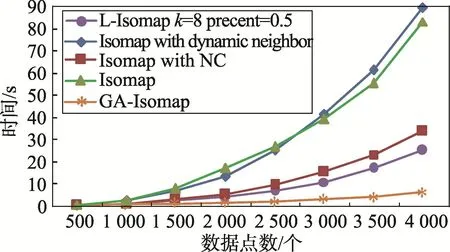
Fig.4 Time comparison by dealingw ith sw iss roll图4 传统sw iss roll数据时间比较

Fig.5 Timecomparison by dealingwith changing-swiss roll图5 changing-sw iss roll数据时间比较
相比之下,GA-Isomap处理两种测试数据时运行时间增量很小,反映出该算法所采用的近邻、地标选取方式和映射计算方式其整体拥有较小的时间开销,也更适合于较大数据量的处理。密度区域内数据点的增多并不会导致地标个数的增加,这可以有效控制地标数量。在数据边界确定时,数据量越大,分布越密集,地标个数越趋于稳定,从而控制了相对地标的映射计算量。即使增加了对地标的测地距离计算和映射处理,对于算法整体的运行效率并没有太大影响。
5 总结与展望
针对数据可视分析应用中视图准确性和结果反馈即时性的需求,本文遵循等距映射的核心思想提出了新的降维映射算法GA-Isomap。本文算法无需任何先验知识和静态参数设置,主动适应数据分布特征,为邻域图构建和地标点选取提出了一个新思路。在进行数据降维可视化时,本文算法兼顾了拓扑稳定性和算法效率,从而能够更准确、迅速地对数据进行可视化。
然而,GA-Isomap为提高计算效率,在划分区域、选取近邻和地标时,需设定额外矩阵或数组记录中间结果,虽避免了后续的重复判断,但导致较大的内存占用。另外,如何有效处理含有噪声的数据也是一个关键问题,因此下一步的工作是研究更加高效的距离测算方式,以及距离矩阵的分解和存储方式,并将所设计的算法用于数据可视化系统开发当中,实际检验本文算法的有效性,并尝试将本文算法用于大数据环境下的可视查询与分析中。
[1]Jiang Lilong,NandiA.SnapToQuery:providing interactive feedback during exploratory query specification[J].Proceedingsof the VLDBEndowment,2015,8(11):1250-1261.
[2]Liu Zhicheng,Jiang Biye,Heer J.imMens:real-time visual querying of big data[C]//Proceedingsof the 15th Eurographics Conference on Visualization,Leipzig,Germany,Jun 17-21,2013.Chichester,UK:The Eurographs Association&John Wiley&Sons,Ltd,2013,32:421-430.
[3]Agarwal S,MozafariB,Panda A,etal.BlinkDB:queriesw ith bounded errors and bounded response times on very large data[C]//Proceedings of the 8th European Conference on Computer Systems,Prague,Apr 15-17,2013.New York:ACM,2013:29-42.
[4]Brehmer M,Sedlmair M,Ingram S,etal.Visualizing dimensionally-reduced data:interviewsw ith analystsand a characterization of task sequences[C]//Proceedings of the 5th Workshop on Beyond Time and Errors:Novel Evaluation Methods for Visualization,Paris,Nov 10,2014.New York:ACM,2014:1-8.
[5]Roweis S T,Saul L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290(5500):2323-2326.
[6]Balasubramanian M,Schwartz E L.The Isomap algorithm and topologicalstability[J].Science,2002,295(5552):7-9.
[7]Tenenbaum JB,De Silva V,Langford JC.A globalgeometric framework for nonlinear dimensionality reduction[J].Science,2000,290(5500):2319-2323.
[8]Samko O,Marshall A D,Rosin PL.Selection of the optimal parameter value for the Isomap algorithm[J].Pattern Recognition Letters,2006,27(9):968-979.
[9]Agarwal A,Phillips JM,Venkatasubramanian S.Universal multi-dimensional scaling[C]//Proceedings of the 16th International Conference on Know ledge Discovery and Data M ining,Washington,Jul25-28,2010.New York:ACM,2010:1149-1158.
[10]Choi JY,Bae SH,Qiu Xiaohong,etal.High performance dimension reduction and visualization for large high-dimensional data analysis[C]//Proceedings of the 10th International Conference on Cluster,Cloud and Grid Computing,Melbourne,Australia,May 17-20,2010.New York:ACM,2010:331-340.
[11]Meng Deyu,Xu Chen,Xu Zongben.A new manifold reconstruction method based on Isomap[J].Chinese Journal of Computers,2010,33(3):545-555.
[12]Shao Chao,Huang Houkuan,Zhao Lianwei.A more topologically stable ISOMAPalgorithm[J].Journal of Software,2007,18(4):869-877.
[13]Gao Xiaofang,Liang Jiye.An improved incrementalnonlinear dimensionality reduction for isometric data embedding[J].Information Processing Letters,2015,115(4):492-501.
[14]Zhan Yubin,Yin Jianping,Long Jun.Dynamic neighborhood selection for nonlinear dimensionality reduction[C]//LNCS 5861:Proceedings of the 6th International Conference on Modeling Decisions for Artificial Intelligence,Awaji Island,Japan,Nov 30-Dec 2,2009.Berlin,Heidelberg:Springer,2009:327-337.
[15]Mekuz N,Tsotsos JK.Parameterless Isomap w ith adaptive neighborhood selection[C]//LNCS 4174:Proceedings of the 28th Symposium of the German Association for Pattern Recognition,Berlin,Sep 12-14,2006.Berlin,Heidelberg:Springer,2006:364-373.
[16]Gao Xiaofang,Liang Jiye.The dynam ical neighborhood selection based on the sampling density and manifold curvature for isometric data embedding[J].Pattern Recognition Letters,2011,32(2):202-209.
[17]Yang Li.Building connected neighborhood graphs for isometric data embedding[C]//Proceedings of the 11th ACM SIGKDD International Conference on Know ledge Discovery in Data M ining,Chicago,USA,Aug 21-24,2005.New York:ACM,2005:722-728.
[18] İnkaya T,Kayalıgil S,Özdemirel N E.An adaptive neighbourhood construction algorithm based on density and connectivity[J].Pattern Recognition Letters,2015,52:17-24.
[19]Silva V D,Tenenbaum JB.Global versus localmethods in nonlinear dimensionality reduction[J].Advances in Neural Information Processing Systems,2002,15:1959-1966.
[20]Orsenigo C.An improved set covering problem for Isomap supervised landmark selection[J].Pattern Recognition Letters,2014,49:131-137.
[21]Dzw inelW,W cisło R.Very fast interactive visualization of large sets of high-dimensional data[J].Procedia Computer Science,2015,51:572-581.
[22]Yang Bo,Xiang M ing,Zhang Yupei.Multi-manifold discrim inant Isomap for visualization and classification[J].Pattern Recognition,2016,55:215-230.
[23]He Jinrong,Ding Lixin,Jiang Lei,etal.Intrinsic dimensionality estimation based on manifold assumption[J].Journal of Visual Communication and Image Representation,2014,25(5):740-747.
附中文参考文献:
[11]孟德宇,徐晨,徐宗本.基于Isomap的流形结构重建方法[J].计算机学报,2010,33(3):545-555.
[12]邵超,黄厚宽,赵连伟.一种更具拓扑稳定性的ISOMAP算法[J].软件学报,2007,18(4):869-877.

WANG Xiyangwasborn in 1992.He isan M.S.candidateatNanjing University of Postsand Telecommunications.His research interest is interactive data visualization and analysis.
王曦杨(1992—),男,江苏南京人,南京邮电大学硕士研究生,主要研究领域为交互式数据可视化与分析。

程春玲(1972—),女,陕西西安人,1996年于南京理工大学获得硕士学位,现为南京邮电大学教授,CCF会员,主要研究领域为数据管理,分布式资源管理和性能优化。

CHEN Xingguo was born in 1984.He received the Ph.D.degree in computer science and technology from Nanjing University in 2014.Now he isa lectureratNanjing University of Posts and Telecommunications.His research interests includemachine learning and reinforcement learning.
陈兴国(1984—),男,江苏南通人,2014年于南京大学获得博士学位,现为南京邮电大学讲师,主要研究领域为机器学习,强化学习。
G lobalAdaptive Isometric M apping A lgorithm for Visualization*
WANG Xiyang,CHENG Chunling+,CHEN Xingguo
School of Computer,Nanjing University of Postsand Telecommunications,Nanjing 210003,China
The Isomap(isometricmapping)and its variant algorithm aremuch influenced by static parameters and thenearestneighbor judgment logic.Asa result,there are problems such as computationalwaste,numericalsensitivity or unstable data topology.In the practicalapplication of interactive data visualization,it is very difficult to fulfill the requirementof real-time interaction and accurate visualization.Therefore,this papermakes an improvementon the original computing framework of isometricmapping,and proposes a globaladaptive algorithm called GA-Isomap(global adaptive-Isomap).In the aspectof neighborhood construction,this paper proposes an incremental construction method and region selection method,by means of the new designed method of local density calculation and the region division.In the aspect of low-dimensional embedding,this paper proposes amapping calculation method based on two-layer graph,which takes the framework graph of landmarksand the relative position relationship into consideration.Compared w ith original Isomap,L-Isomap,Isomap with dynamic neighbor and Isomap w ith NC,simulation results show that the GA-Isomap algorithm can effectively balance the data topology stability and operationalefficiency in visualization.
isometricmapping;data visualization;topologicalstability;datamanifold
nling was born in 1972.She
the M.S.degree in computer application from Nanjing University of Science and Technology in 1996.Now she is a professor at Nanjing University of Posts and Telecommunications,and themember of CCF.Her research interests include datamanagement,distributed resourcemanagement and performanceoptimization.
A
:TP391
摘 要:等距映射(isometric mapping,Isomap)及其衍生的维度约简算法受静态近邻值、地标比重值或近邻判断逻辑的影响,存在计算浪费、数值敏感或数据拓扑不稳定的情况,在数据可视化分析的实际应用中很难满足交互实时性和视图准确性的需求。为此,对等距映射的原始计算框架进行改进,提出了具有全局自适应性的GA-Isomap(global adaptive-Isomap)算法。邻域图构建方面,设计了数据局部密度值计算和区域划分方法,提出了渐进式的邻域图构造方法和区域地标点选取方法;降维映射方面,引入地标框架图并利用相对位置关系,提出了基于双层图的映射计算方式。仿真结果表明,与Isomap、L-Isomap、Isomap w ith dynam ic neighbor和Isomap w ith NC算法相比,该算法在进行数据可视化映射时能有效兼顾数据拓扑稳定性和运行效率。
