滚动轴承性能时间序列的模糊假设检验
2017-07-25栗永非杨彬彬
栗永非,杨彬彬
(新乡职业技术学院,河南 新乡 453006)
滚动轴承的性能指标包括摩擦力矩、振动和噪声等,对轴承的运行具有重要影响[1-6],因此滚动轴承性能时间序列的演化问题成为了研究的热点[7-8]。
目前,传统的假设检验是以已知大量采样数据和概率分布为前提的,对于概率分布未知、趋势未知和小样本的情况,基于经典统计理论的假设检验可能是无效的。为此,以模糊系统的基本原理为依据,提出改进的模糊关系,建立模糊假设检验模型,提出系统属性模糊假设检验的准则、否定域与模糊置信水平,采用Monte Carlo仿真和试验研究验证该模型的有效性。
1 模糊假设检验模型
1.1 基本原理
滚动轴承性能参数的时间序列为
X=(x(1),x(2),…,x(t),…,x(T));
T>5,X⊂R,
(1)
式中:T为数据的个数;R为模糊集。
为评估滚动轴承质量的历史演变,从X中任意取Xi和Xj,可得
Xi=(xi(1),xi(2),…,xi(k),…,xi(K));
Xi⊂Ui;i=1,2,…,
(2)
Xj=(xj(1),xj(2),…,xj(k),…,xj(K));
Xj⊂Uj;j=1,2,…;k=1,2,…,K;2 (3) 式中:k为新数据序列的个数;Ui为Xi的属性集;Uj为Xj的属性集。 由于Xi和Xj是关于下标i和j的时间序列,能够从小到大形成连续的有序对(X1,X2), (X2,X3), (X3,X4),…,因此,可以通过识别这些有序对的多样性实现对滚动轴承质量演变的有效评价。为便于叙述,i和j统一用h表示,则(2)式和(3)式表示为 Xh=(xh(1),xh(2),…,xh(k),…,xh(K)); k=1,2,…,K;Xh⊂Uh;h=i,j, (4) 式中:Xh为K个小样本;Uh为随机的概率分布。在概率分布及趋势规律未知的情况下,研究xi和xj是否具有相同的属性。 在模糊集理论[9-10]中,通过隶属函数研究模糊实体从真到假或从假到真的转变规律。基于乏信息的模糊假设检验,其否定域可以通过对数据信息转折点确立。 设定参考序列为 X0=(x0(1),x0(2),…,x0(k),…,x0(K)), (5) x0(k)=xi(1), (6) 以序列Xi中xi(1) 作为参考点或演化的起点。 根据灰色系统理论,定义隶属函数为 γ0h(k,ξ)= 0<γ0h(k,ξ)≤1, (7) 式中:ξ为分辨系数,ξ∈[0,1]。 隶属度为 (8) 隶属差为 dij(ξ)=|γ0i(ξ)-γ0j(ξ)| , (9) 式中:dij(ξ)为关于ξ的函数且dij(ξ)∈[0,1]。由于很难区分时间序列属性的量变和质变,且量变和质变的转折点是不确定的,因此给定一个重要参数 (10) 式中:ξ*为最优分辨系数;dij max为最优隶属度的绝对差。 当dij=dij max时,时间序列Xi和Xj的差异最大,若仍然存在(Xi,Xj)⊂U(U为属性集),则拒绝I型错误[9-10]。 为了深入研究Xi和Xj之间的属性变化,根据模糊集合理论,模糊关系定义为 (11) rij∈[0,1],为等价系数(或Xi和Xj的隶属度关系),可由以下模型得到 (12) 式中:η为权重系数。 由(9)~(12)式可知i=j,rij=1。 这表明R具有自反性。此外,R具有对称性和传递性,因此,R是一个等价关系。R是对模糊关系的改进,被称为改进等价关系(空间)。 为解决模糊集理论的问题,采用权重来定义经验置信水平。 考虑到dij max∈[0,η],由(12)式得 dij max=(1-rij)η, (13) 使rij=λ,定义经验置信水平为 PE=PE(η)=(1-λη)×100%。 (14) 若给定PE,则 (15) 若 rij≥λ, (16) 则Xi和Xj属性相同,即(Xi,Xj)⊂U; 若 rij<λ, (17) 则Xi和Xj属性不同,即(Xi,Xj)⊄U。 该准则称为基于乏信息的时间序列模糊假设检验准则。 关于集合U的特征函数为 (18) 式中:λ*为最优水平。 在经验置信水平PE下,若Xi和Xj关系密切,则用1表示;若不密切,则用0表示。 给定最优水平 λ*=0.5 , (19) 在转折点,rij=0.5,则由(13)式得dij max=0.5η,该点即dij max的临界点。 由(10)~(19)式可知,经验置信水平引入了分解定理。 定义原(零)假设H0和备择假设H1 H0: (Xi,Xj)⊂U, (20) H1: (Xi,Xj)⊄U, (21) 则(18)式是模糊假设检验的否定域。 设显著水平α∈[0,1],有 PE=(1-α)×100%, (22) 最常用的显著水平为0.05。 使时间序列T=500,借助计算机仿真系统,生成符合正态分布的10个数据序列(其中数学期望E=0,标准偏差s=0.01),即获得Xi和Xj(i=1,2,…,m;j=1,2,…,m;m=10)。那么,可以计算出最大差值,结果见表1。 表1 正态分布的最大差值(T=500) 表1中,有55个数据(不包括主对角线的元素),即N=55。通过0.01的间隔宽度,将这些数据分为8组,可以得到每组数据的数量wl(l=1,2,…,8),见表2。 表2 正态分布的相关结果(T=500) 设频率为 (23) 定义经验概率PT为 (24) 当PT=95%时,这个调查的效率是非常明显的。表2中,第6组数据的中位数δ6=δ=0.055 ,PT=96.4%>95%。由(12),(14)式可得dij max=δ=0 .055,PE=94.5%,相应地,通过(14)式可以得到η=0.11。结果见表3。 表3 各种分布的数据和结果(T=500) 采用同样的方法,进行瑞利分布、三角分布和均匀分布的Monte Carlo仿真,结果见表3。对于这4种分布,当PT=96.4%时,PE在93.5%~97.5%之间变动,PE的平均值为95.4%,与PT值很接近,差值不超过1%。因此,基于Monte Carlo仿真法获得的PE值一致,证明了(14)式的正确性。 另外,一般置信水平为PE=95%,相应地η=0.1。 通过赋予水平λ新的意义,可应用文中定义的经验置信水平来解决置信水平的计算问题,而采用模糊集合理论和统计理论都无法解决。 研究涉及滚动轴承的2个性能参数,即噪声和摩擦力矩。为了验证提出模型的正确性,给定2个检验统计量 (25) (26) 式中:Xm为平均值;s为标准差。这2个检验统计量的变化可认为是估计时间序列的演化,变化越大演化越严重,反之亦然。 试验轴承为圆锥滚子轴承30204,试验转速为1 800 r/min,加载60 N的轴向载荷,随机抽取100套轴承采用传声器4165测量轴承的噪声时间序列,测得100个时间序列,如图1所示。 图1 圆锥滚子轴承的噪声时间序列 描述1:从表面上看,对于噪声时间序列X,当1≤t≤10时,噪声处于低且平稳过程,当10 采用提出的模糊假设检验模型来评估演化历史,为了研究方便,将时间序列X分成子序列 X1=(x1(1),x1(2),…,x1(10));1≤t≤10, X2=(x2(1),x2(2),…,x2(10));11≤t≤20, X3=(x3(1),x3(2),…,x2(40));21≤t≤60, X4=(x4(1),x4(2),…,x4(40));61≤t≤100。 令α=0.05,则PE=95%,η=0.1。检验结果如下: 检验1)H0:(X1,X2)⊂U对H1:(X1,X2)⊄U。 考虑到X1和X2的关系,采用模糊假设检验模型获得如下结果:x0(k)=40 dB,ξ*=0.250 1,γ01(ξ*)=0.547 3,γ02(ξ*)=0.242 2,d12max=0.305 1,r12=r21=0。显然,r12=0<0.5满足(18)式条件,则H0被拒绝,表明在PE=95%下,时间序列从X1到X2发生了重大变化(当1≤t≤20时,噪声处于非平稳过程),与描述1一致。 检验2)H0:(X2,X3)⊂U对H1:(X2,X3)⊄U。 考虑到X2和X3的关系,采用模糊假设检验模型获得如下结果:x0(k)=49 dB,ξ*=0.100 1,γ03(ξ*)=0.348 2,γ04(ξ*)=0.312 9,d34max=0.035 3,r34=r43=0.647。显然,r43=0.647>0.5不满足(18)式条件,则H0被接受,表明在PE=95%下,时间序列从X2到X3没有发生重大变化(当21≤t≤60时,噪声处于平稳过程,与描述1一致。 检验3)H0:(X3,X4)⊂U对H1:(X3,X4)⊄U。 考虑到X3和X4的关系,采用模糊假设检验模型获得如下结果:x0(k)=49 dB,ξ*=0.100 1,γ03(ξ*)=0.348 2,γ04(ξ*)=0.312 9,d34max=0.035 3,r34=r43=0.647。显然,r43=0.647>0.5不满足(18)式条件,则H0被接受,表明在PE=95%下,时间序列从X3到X4没有发生重大变化(当60≤t≤100时,噪声处于平稳的过程),与描述1一致。 从检验1~3中可以看出,在95%的置信水平下,提出的推理模型是正确的,与事实相符,这也可以通过校验统计学进行证明。 根据(25)式和(26)式,子序列X1,X2,X3,X4的均值和标准差分别如图2和图3所示。 当1≤t≤10(h=1)时,Xm=43 dB,s=2.684 dB;当11≤t≤20(h=2)时,Xm=48.333 dB,s= 图2 圆锥滚子轴承噪声子序列Xh的均值 图3 圆锥滚子轴承噪声子序列Xh的标准差 1.699 dB。X1和X2的均值和标准差均相差很大,这表明时间序列从X1到X2发生了重大变化;当21≤t≤60(h=3)时,Xm=47.942 dB ,s=2.175 dB;X2和X3的均值和标准差相差不大,这表明时间序列从X2到X3没有发生重大变化;当61≤t≤100(h=4)时,Xm=47.258 dB,s=2.25 dB,X3和X4的均值标准差相差很小,这表明时间序列从X3到X4没有发生重大变化。 模糊假设检验模型被证明。 试验轴承为7000型角接触球轴承。其动态摩擦力矩试验装置主要包括SS1798B直流稳压电源、反作用飞轮控制箱和真空试验装置等。按设定秒为单位输出电信号,并按设定的30 min为单位间隔均匀采集了T=200个数据,试验获得摩擦力矩的时间序列为X,如图4所示。 图4 滚动轴承摩擦力矩时间序列 描述2:从表面上看,对于时间序列X,当1≤t≤50时,摩擦力矩逐渐增大;当51≤t≤100时,摩擦力矩逐渐减小;当101≤t≤200时,摩擦力矩处于平稳过程,因此,摩擦力矩时间序列X经历了复杂的时间演变,在演变过程中,可能导致轴承的初始磨损[2]。 采用提出的模糊假设检验模型来评估上面的演化历史,为了研究方便,将时间序列X分成子序列 X1=(x1(1),x1(2),…,x1(50));1≤t≤50, X2=(x2(1),x2(2),…,x2(50));51≤t≤100, X3=(x3(1),x3(2),…,x3(50));101≤t≤150, X4=(x4(1),x4(2),…,x4(50));151≤t≤200。 使α=0.05,则PE=95%,η=0.1。检验结果如下: 检验4)H0:(X1,X2)⊂U对H1:(X1,X2)⊄U。 考虑到X1和X2的关系,采用模糊假设检验模型获得如下结果:x0(k)=143 mA,ξ*=0.250 1,γ01(ξ*)=0.520 8,γ02(ξ*)=0.461 7,d12max=0.059 1,r12=r21=0.409。显然,r12=0.409<0.5满足(18)式条件,则H0被拒绝,表明在PE=95%下,时间序列从X1到X2发生了重大变化(当1≤t≤50时,摩擦力矩处于非平稳过程),与描述2一致。 检验5)H0:(X2,X3)⊂U对H1:(X2,X3)⊄U。 考虑到X2和X3的关系,采用模糊假设检验模型获得如下结果:x0(k)=142.9 mA,ξ*=0.000 1,γ02(ξ*)=0.080 5,γ03(ξ*)=0.000 6,d23max=0.079 9,r23=r32=0.201。显然,r32=0.201<0.5满足(18)式条件,则H0被拒绝,表明在PE=95%下,时间序列从X2到X3发生了重大变化(当51≤t≤150时,摩擦力矩处于非平稳的过程),与描述2一致。 检验6)H0:(X3,X4)⊂U对H1:(X3,X4)⊄U。 考虑到X3和X4的关系,采用模糊假设检验模型获得如下结果:x0(k)=143.2 mA,ξ*=0.200 1,γ03(ξ*)=0.416 8,γ04(ξ*)=0.411 1,d34max=0.005 7,r34=r43=0.942。显然,r34=0.942>0.5不满足(18)式条件,则H0被接受,表明在PE=95%下,时间序列从X3到X4没有发生重大变化(当101≤t≤200时,摩擦力矩处于平稳的过程),与描述2一致。 从检验4~6可以看出,在95%的置信水平下,提出的推理模型是正确的,与事实相符,这也可以通过校验统计学进行证明。 根据(25)式和(26)式,子序列X1,X2,X3,X4的均值和标准差分别如图5和图6所示。 图5 滚动轴承摩擦力矩子序列Xh的均值 图6 滚动轴承摩擦力矩子序列Xh的标准差 当1≤t≤50(h=1)时,Xm=142.992 mA,s=0.521 mA;当 (即h=2)时,Xm=142.898 mA,s=0.622 mA。X1和X2的均值相差很小,但标准差相差很大,这表明时间序列从X1到X2发生了重大变化。 当101≤t≤150(h=3)时,Xm=142.568 mA,s=0.523 mA。X2,X3的均值和标准差均相差很大,这表明时间序列从X1到X2发生了重大变化。 当151≤t≤200(h=4)时,Xm=142.536 mA,s=0.466 mA。X3,X4的均值和标准差均相差很小,这表明时间序列从X3到X4没有发生重大变化。 模糊假设检验模型被证明。 通过在模糊假设检验拒绝域中引入权重,确定了改进的等价关系和经验置信水平之间的关系,同时将经验置信水平引入模糊集合理论的分解定理,为乏信息系统的模糊决策奠定了新的基础。Monte Carlo仿真证明,在95%的经验置信水平下,提出的模糊假设检验模型能够应用于正态分布、瑞利分布、三角分布和均匀分布4种典型概率分布。滚动轴承性能时间序列演化的试验研究表明,在乏信息条件下该模型能够很好地评估模型的历史演化平稳和非平稳的过程。1.2 改进的模糊关系
1.3 经验置信水平
1.4 模糊假设检验准则
1.5 否定域
2 经验置信水平的Monte Carlo仿真



3 滚动轴承性能时间序列的试验研究
3.1 滚动轴承噪声的演化评估
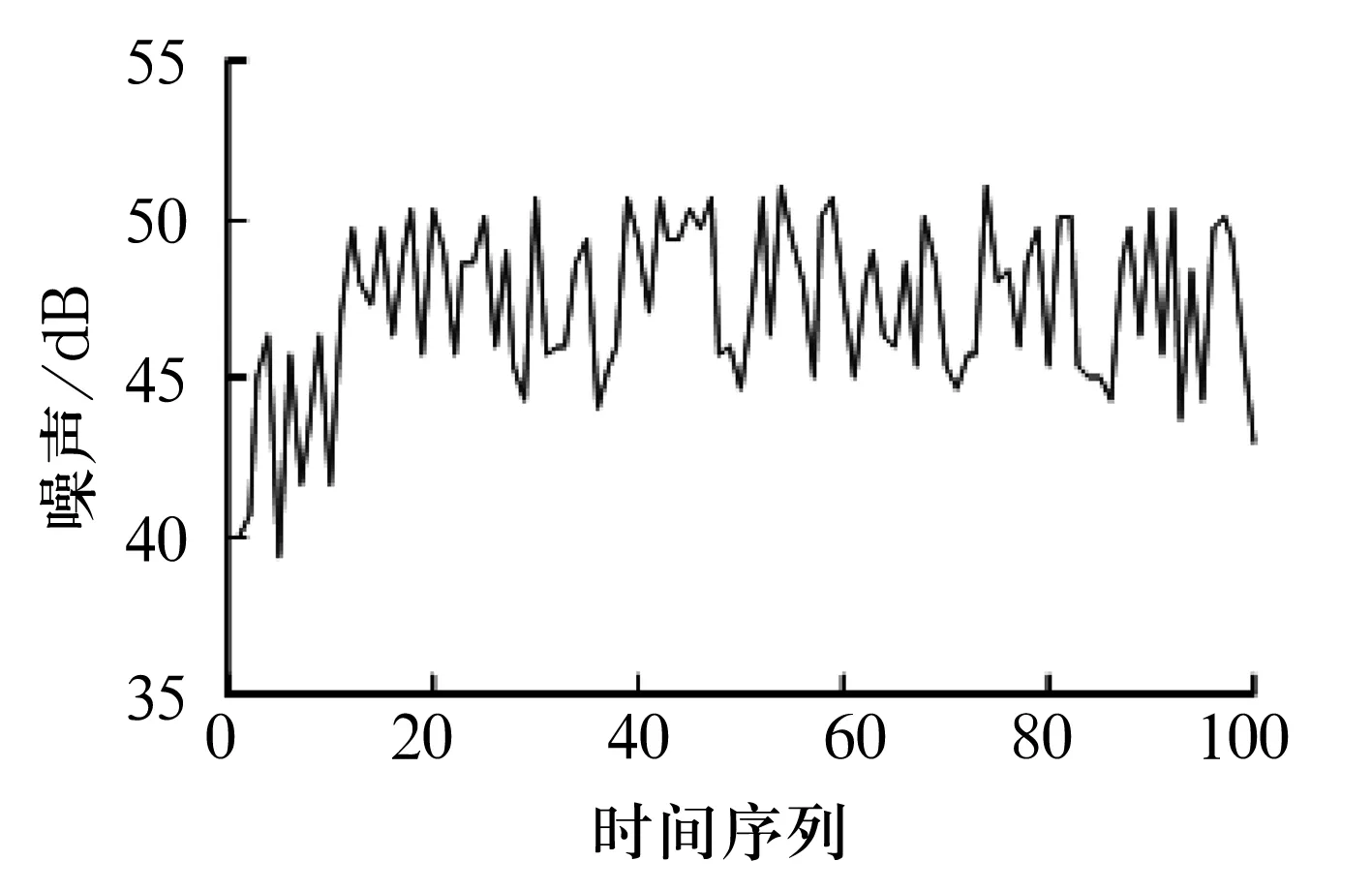
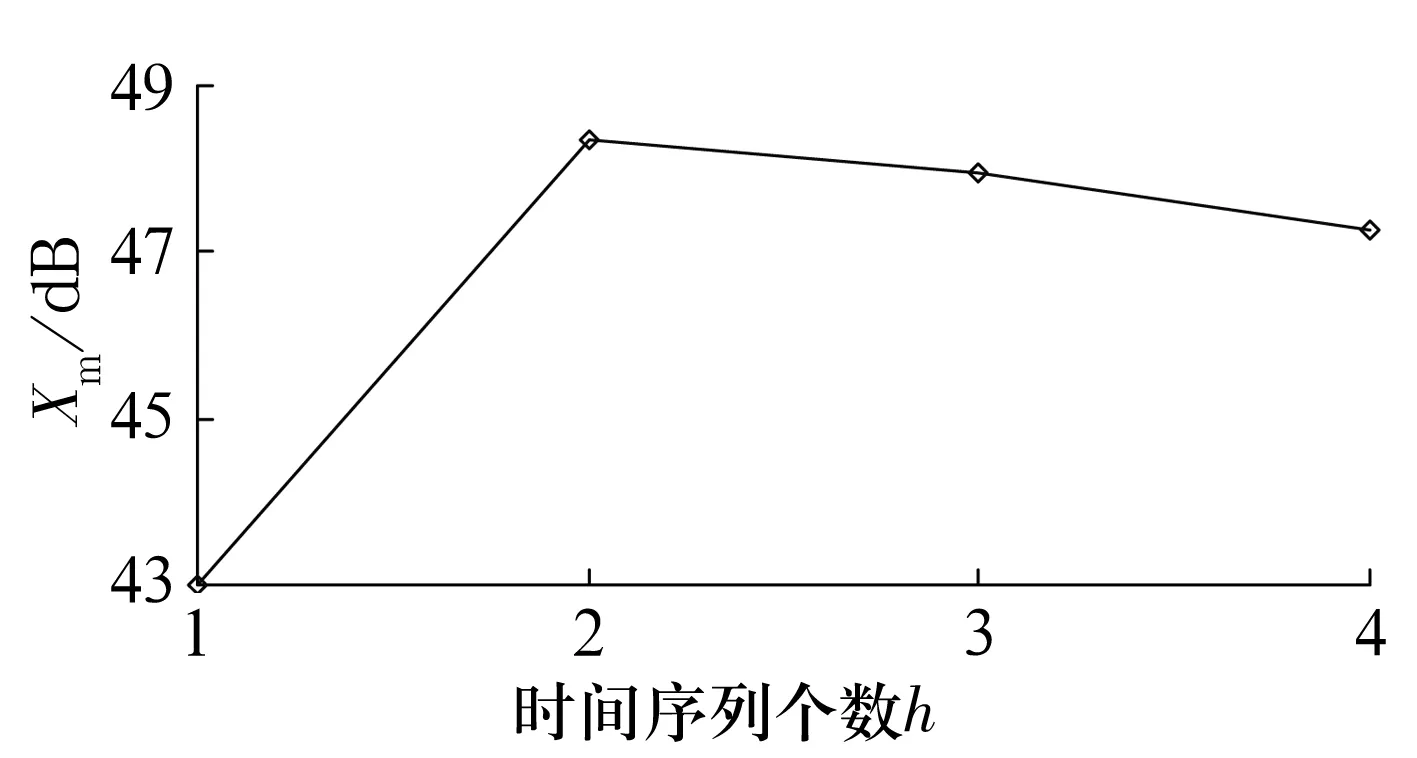

3.2 滚动轴承摩擦力矩的演化评估
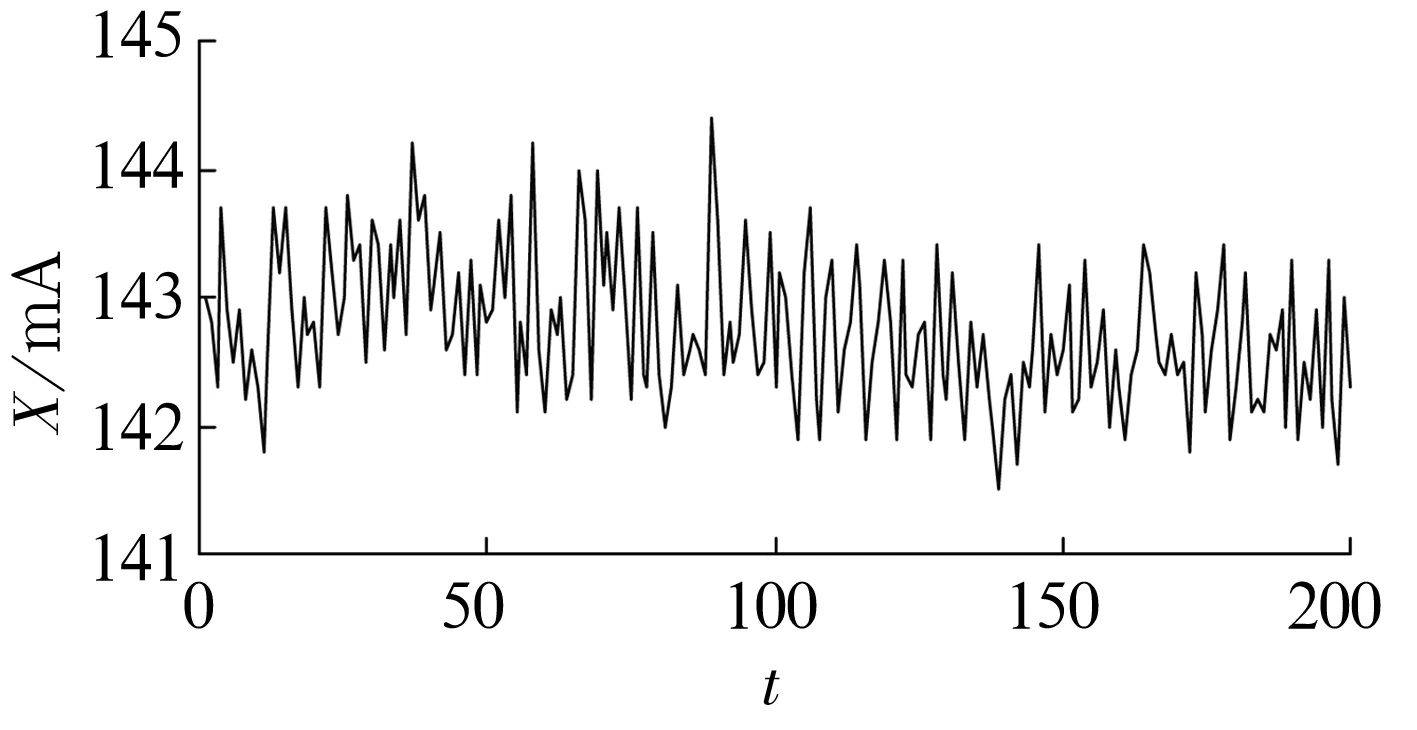
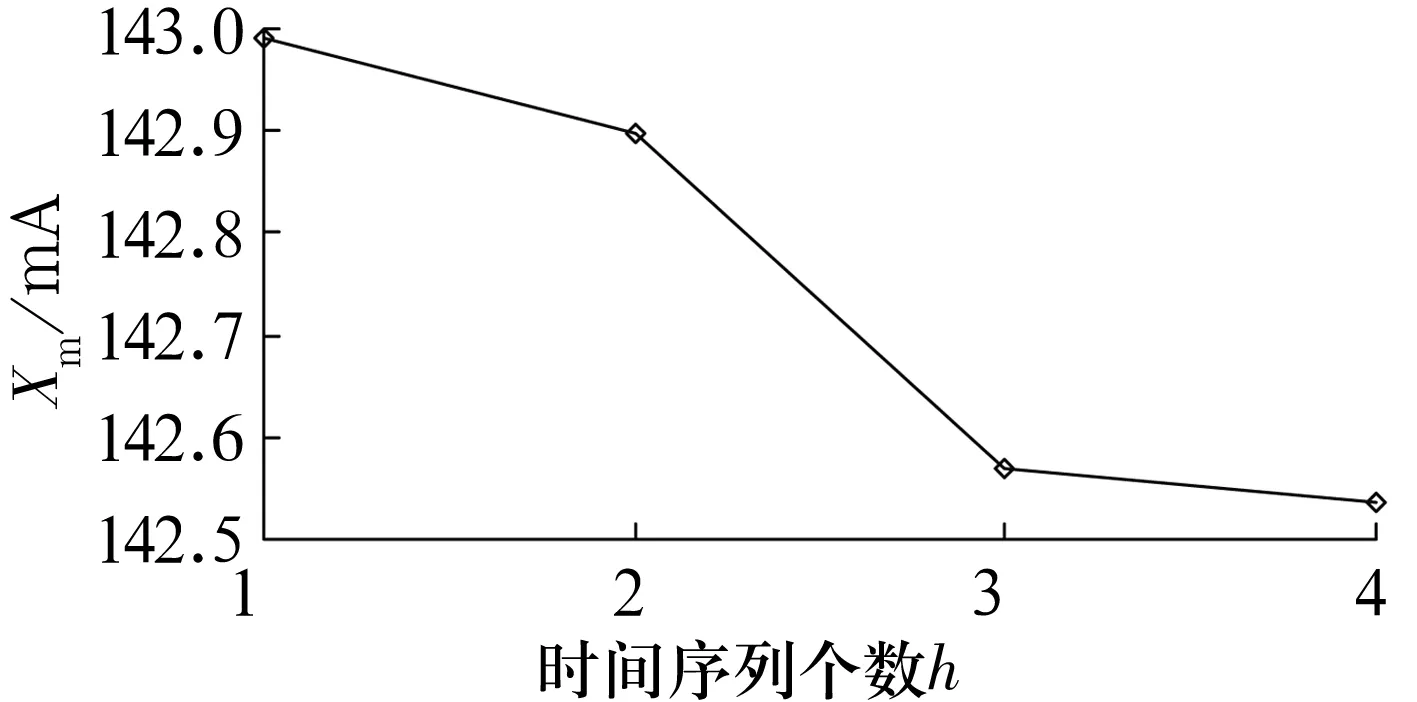

4 结束语
