基于ABAQUS的汽车轮毂轴承套圈早期裂纹动力学分析

2017-07-25马君达颉潭成孙立明徐彦伟

轴承 2017年7期

马君达，颉潭成，孙立明,2，徐彦伟

(1.河南科技大学机电工程学院，河南洛阳 471003;2.洛阳轴研科技股份有限公司，河南洛阳 471039)

轮毂轴承是车辆的重要支承和传动部件。若轮毂轴承出现故障，将影响到汽车的安全性[1]。滚动面表面裂纹是轴承故障的重要原因之一，裂纹起源于滚动面表面，当表面存在原始缺陷如微小预裂纹、划伤、加工刀痕、粗糙凸峰等时，在滚动过程中由于接触应力的反复作用产生小裂纹，进而向表面下扩展导致疲劳剥落[2-3]，从而影响轴承表面的接触特性和振动特性，故有必要对含裂纹轴承进行动力学分析[4]。

有限元法为轴承的设计制造及故障分析提供了强有力地支持。文献[5]通过有限元法研究了圆柱滚子轴承在静力下内、外圈的应力和位移分布；文献[6]通过建立滚动轴承的混合模型提出了一种计算存在表面缺陷的滚动轴承滚道上接触应力、接触角的新方法；文献[7]通过选用双线性等强化模型和双线性随动强化模型2种材料塑性变形模型分析了塑性变形对轴承内部应力的影响；文献[8]基于显式动力学建立了滚动体故障和点蚀故障的轴承故障模型，分析了有、无故障时轴承的不同特性。上述研究分别从静力学和动力学对轴承的应力状态、材料性能、缺陷故障等进行分析，但对轴承早期裂纹的有限元分析较少。鉴于此，建立含滚动表面裂纹的轮毂轴承的多体动力学接触有限元模型，基于ABAQUS对轮毂轴承早期裂纹进行显式动力学分析。

1 显式动力学

1.1 求解器选择

轴承接触应力与接触区域相互影响，具有高度非线性的特质，轴承零件之间的接触关系时刻变化，且受内部载荷分布、润滑及材料性能的影响，接触工况复杂。基于ABAQUS使用隐式求解法可以建立平稳的接触关系，减小由冲击效应产生的应力波的影响，但Newton-Raphson求解法[9-10]在每个增量步中都进行迭代，需要的存储空间大，较大的位移和转动会使模型难以收敛，而ABAQUS/Explicit是高效求解复杂非线性问题的计算工具，显式求解不需要进行迭代计算，且接触方式简单，不存在收敛问题。

1.2 动力学基本理论

系统求解方程为

(1)

ABAQUS/Explicit采用中心差分法求解，加速度和速度为

(2)

(3)

式中：Δt为时间间隔。

将(2)，(3)式代入(1)式可得各离散点的时间点解递推公式为

(4)

由于中心差分法是条件稳定算法，其稳定条件为

(5)

式中：Tn为有限元系统最小固有振动周期；Δtcr为某个临界值，如采用壳单元时，

(6)

式中：lmin为最小单元长度；E为材料弹性模量；ρ为材料密度；ν为泊松比。

2 含裂纹轴承的显式动力学模型

重载汽车后桥轮毂轴承为成对单列圆锥滚子轴承，型号为32218，仅对其中的一套进行建模分析，其基本结构参数见表1。

表1 结构参数

2.1 材料选择

根据结构参数建立模型，忽略倒角，径向游隙设置为0，轮毂轴承的套圈及滚子材料为GCr15SiMn，弹性模量E=216 GPa，泊松比ν=0.3，密度ρ=7.82×103kg/m3。

2.2 分析步及相互作用

模型设置为2个step，每个step为10 ms，step1用来施加载荷，静摩擦因数μ=0.01；模型稳定后，step2施加转速并采用动摩擦因数μ=0.005。接触类型为通用接触，显式计算中的通用接触模式可以方便地建立接触关系，且不存在收敛问题。保持架不影响文中的研究对象，为减少计算，将保持架设为刚体并约束其周向运动。

2.3 载荷及边界条件

轴承外圈固定，约束外表面6个方向自由度；对耦合点RP1施加沿y轴的集中载荷270 kN，模拟轴承的径向加载；施加x轴方向的旋转角速度3 000 r/min，即轴承额定转速；ABAQUS/Explicit分析模型中的边界条件不允许出现跳跃式的突然变化，跳跃处的加速度无限大，定义幅值曲线避免跳跃，如图1所示。

图1 幅值曲线

2.4 网格划分

滚子与轴承内、外圈及保持架均有接触，接触区网格越密集，计算结果越精确，但为减小计算量，需对模型进行分割，使接触区域网格密度增大，而非接触区域网格疏化，且满足接触区域网格宽度小于轴承接触椭圆区短轴半宽的一半；单元类型选择线性缩减积分单元C3D8R，缩减积分单元可以缓解完全积分单元可能导致的单元过于刚硬和计算挠度偏小的问题[11]，单元形状为六面体，扫略形成网格，模型整体单元数目为861 372，节点数目为944 497。

2.5 裂纹预制

通过预制表面线条状细小缺口，模拟轴承外圈滚道面的初始裂纹缺陷，分析其对应力分布及振动特性的影响，轴承载荷分布如图2所示，外圈上受力最大处在径向载荷的正下方，在外滚道受力最大处表面沿接触线方向去除材料，缺口形状为等边倒三角形，深度均为0.01 mm，顶尖角度为20°，则裂纹宽度为0.003 5 mm，长度方向贯穿两端面，以实现裂纹尖端的模拟。裂纹表面网格比正常接触表面划分网格更密集，最小单元尺寸宽度为0.003 12 mm，小于裂纹宽度，轴承有限元离散结构如图3所示。

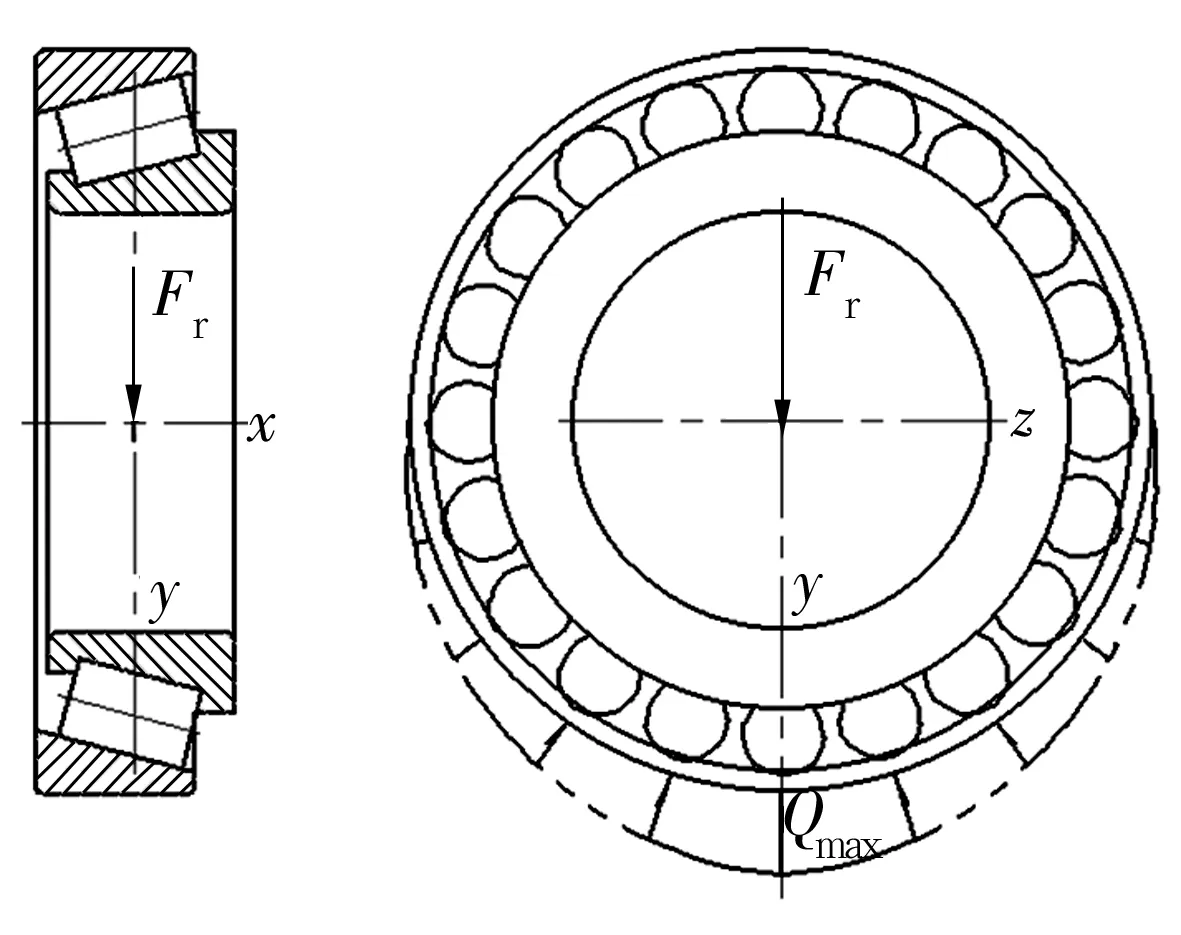
图2 载荷分布图

图3 轴承有限元离散结构

3 仿真结果及分析

3.1 应力分析

1)在载荷270 kN、转速3 000 r/min下，沿载荷方向的下半部分为受载区域，在10 ms时正常轴承外圈的接触应力云图如图4a所示，滚子与外圈接触区域呈椭圆形，接触应力最大处在外滚道最低处，且应力从中间向两端减小；含裂纹轴承在10 ms时外圈的接触应力云图如图4b所示，从图中可看出，接触区域呈线性椭圆分布，最大接触应力从1 443 MPa增大到5 457 MPa，较大的接触应力会造成轴承外圈裂纹扩展甚至断裂。

图4 外圈接触应力云图

2)轴承在整个运动中外圈滚道最低点的等效应力如图5所示，在step1阶段，正常轴承加载时间为1 ms，之后载荷大小保持不变，等效应力表现为加载过程呈线性，加载完之后在小范围内振荡；而含裂纹轴承在加载瞬间，等效应力突然增大，在1 ms内存在多次波动，呈非线性变化，之后维持在小范围内振荡，应力值大于正常轴承。在step2转动阶段，正常轴承与含裂纹轴承的应力循环周期相同，含裂纹轴承整体平均应力水平比正常轴承高很多，正常轴承滚道不与滚子接触时等效应力基本为零，说明滚道表面未变形，而含裂纹轴承的等效应力约为500 MPa，且不随接触载荷的消失而减小，说明表面已发生变形。

图5 轴承等效应力随时间变化

3)在转速3 000 r/min条件下，分别对含裂纹轴承施加10，100，270 kN载荷，外圈滚道最低点的等效应力如图6所示。

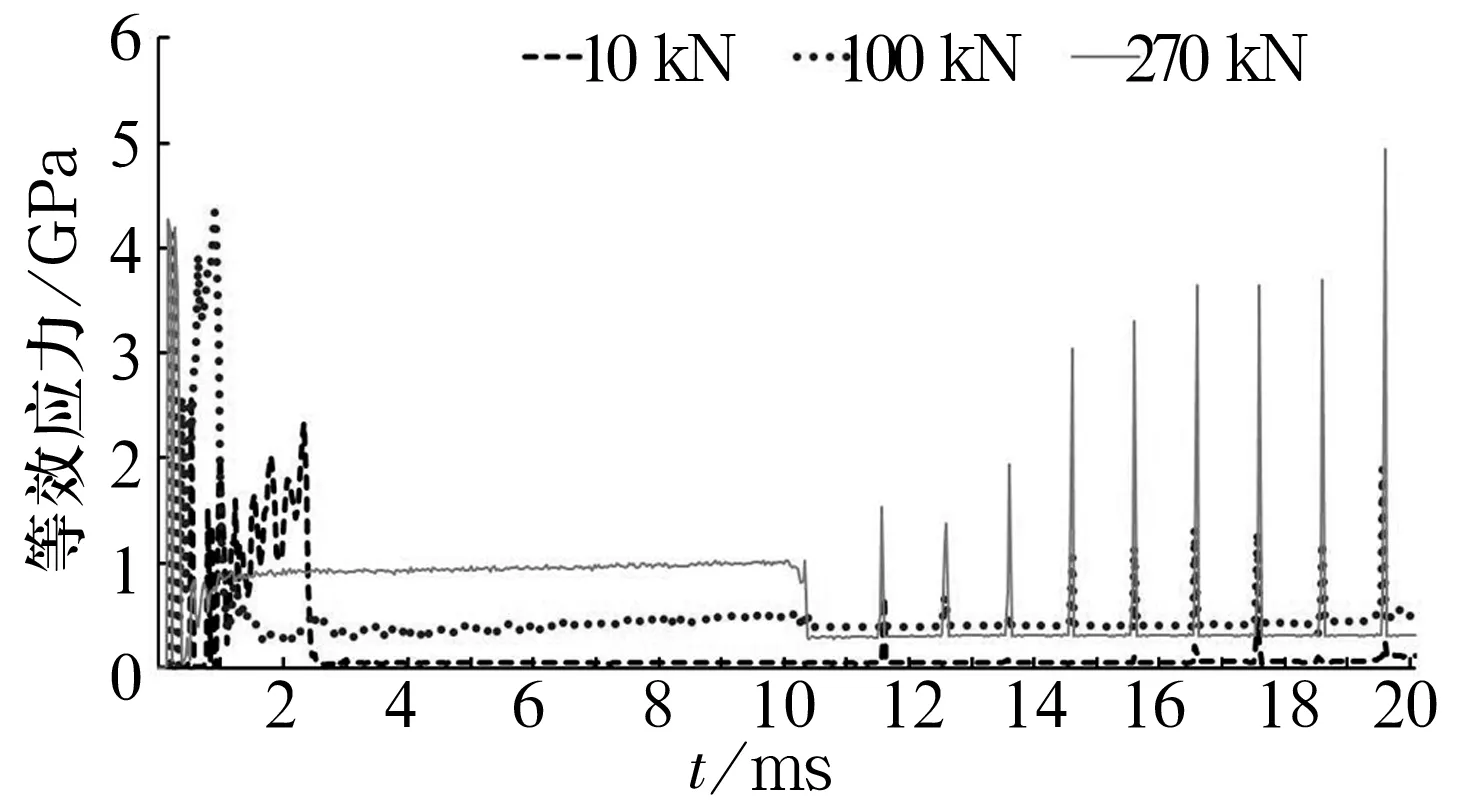
图6 不同载荷下含裂纹轴承等效应力随时间的变化

在step1阶段，不同载荷下应力达到稳定的时间不同，随载荷增大，等效应力达到稳定的时间反而缩短；且随载荷增大，应力波动情况也发生变化，载荷越大，应力波动情况出现的越早，应力的波动范围也越大。

在step2阶段，转速相同，应力循环周期基本不变，应力值不同。在10 kN载荷时，除滚子与滚道接触时应力值变化，在非承载时应力基本为零，与正常轴承相同，说明轴承表面未发生变化；在100，270 kN载荷作用下，在非承载时轴承应力并未恢复到很小，说明裂纹处单元应力在超越屈服应力之后已出现不可恢复的塑性变形，在材料内部有残余应力，这将导致表面裂纹向深处扩展；随载荷增加，在接触时单元的应力也随之增加，这将加速轴承滚道和滚子的破坏。

3.2 振动特性分析

为准确分析表面裂纹对轴承运动特性的影响，对滚子在y方向加速度进行分析。模型在step2施加转速，为避免转速跳跃，前1 ms为转速的持续增加阶段，之后9 ms转速稳定。分别在正常轴承和含裂纹轴承选取滚子节点93，加载10，100，270 kN，分析y方向加速度随时间的变化。

滚子节点93位于与裂纹接触的第2个滚子表面宽度中心处，节点位置如图7所示。转速相同，在270 kN载荷作用下，正常轴承加速度曲线如图8所示，不同载荷下含裂纹轴承加速度曲线如图9所示。

图7 节点位置

图8 正常轴承滚子节点加速度曲线(270 kN)

由图9可知：1)在滚子受载期间，随载荷变化，y轴方向加速度不断变化，影响到轴承的整体振动；在该滚子离开受载区后，加速度值保持在很小的范围内波动，可忽略不计。2)在不同载荷作用下，存在裂纹使得加速度有不同程度的变化，在10 kN载荷作用下，加速度基本上不受影响，这也证明了加速度传感器对于早期轴承故障的不敏感;随载荷增大，加速度波动范围也增大，且持续时间增长，说明随载荷增加，受载滚子个数增加。3)在载荷270 kN作用下，正常轴承和含裂纹轴承加速度差别较大，裂纹轴承加速度比正常轴承大4～6倍，在滚子经过裂纹时，加速度从5×109mm/s2增大到120×109mm/s2，加速度变化会造成轴承的振动冲击，影响车辆的稳定行驶并伴随着严重噪声。