基于有限元分析内部裂纹对球轴承外圈振动特征的影响

叶九龙, 张杰

(1.成都工业职业技术学院 汽车工程系，成都 610061；2.西南交通大学 牵引动力国家重点实验室，成都 610031)

滚动轴承在航空航天、机械装备等领域广泛应用[1]。在交变载荷下，轴承套圈易出现表面裂纹和内部裂纹[2]。当出现表面裂纹和内部裂纹时，套圈局部刚度改变，会影响其结构的模态参数和振动特征[2],故可通过监测结构刚度的变化实现对轴承套圈损伤的检测。

通过开展裂纹引起的轴承套圈振动特征变化的研究，可诊断和识别套圈的裂纹失效形式。国内外学者进行了大量研究，文献[1]推导了圆环弯扭振动的表达式，计算了不同边界条件的圆环特征值；文献[3]研究了轴对称圆环的平面弯曲振动特征，得到圆环面内弯曲振动的固有表达式。若选取合适的轴承套圈参数时，轴承套圈存在频率接近为0的近似正交模态；文献[4]研究了轴向极化压电陶瓷薄圆环的径向振动特征，推导了其机电等效电路，获得了圆环振子的共振与反共振频率方程，并对其结果进行了试验验证；文献[5]采用有限元法对系列均质平面圆环的振动特征进行了分析，研究了叠层平面圆环的振动特征以及叠层对其振动的影响，并进行试验研究；文献[6]基于有限元法仿真分析了圆环的谐振频率；文献[7]研究了正常圆环和圆环梁结构的自由振动特征。

大多数研究主要集中在正常轴承套圈的振动特征[1-12]，而对裂纹引起的轴承外圈的振动特征变化研究较少，尤其是内部裂纹引起的振动特征变化。鉴于此，以含内部裂纹的轴承外圈为研究对象，基于有限元法建立正常轴承外圈和含内部裂纹轴承外圈的有限元模型，仿真分析内部裂纹对外圈固有频率、模态振型及模态振型曲率的影响。

1 理论分析

1.1 球轴承外圈的振动特征

自由支承条件下，轴承外圈存在径向和轴向弯曲振动，径向弯曲振动的n-1阶固有频率为[12]

(1)

式中：n为固有频率的阶次；E为弹性模量；ρ为密度；S为横截面积；Ia为截面惯性矩；R为中径半径。

基于有限元法的轴承外圈自由模态仿真分析，首先采用有限元法对外圈进行单元离散，再构建外圈的数学模型，求解外圈的特征值与特征向量，得到的特征值为外圈的固有频率，特征向量为外圈的振型。

以广义坐标x描述n个自由度的受迫振动系统，在外载荷的作用下，通过动力学理论得到外圈的运动微分方程为[11]

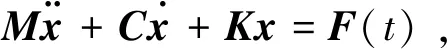
(2)

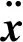
模态分析为轴承外圈的固有特性，与所受外载荷无关，且在求解外圈的固有特性时，阻尼对外圈的固有特性影响较小。故(2)式转化为[11]

(3)

令

x=Asinω(t-t0)，

(4)

式中：A为第n阶位移向量x的幅值向量，即振型；ω为与向量A对应的自然频率；t为时间；t0为初始条件确定的时间常数。

将(4)式代入(3)式得系统的广义坐标方程为

(K-ω2M)A=0，

(5)

1.2 球轴承外圈模态振型曲率[13-14]

假设通过有限元法得到轴承外圈的模态振型矢量为φ，根据差分原理，计算外圈的曲率模态矩阵，令Sij为矩阵φ的元素，则外圈的曲率模态矩阵为

(6)

式中：i为外圈有限元模型的节点号，i= 1，2，…，n；j为模态频率的阶次,j=1，2，…，6 ；li为外圈有限元模型的单元长度。

2 模型建立

正常轴承外圈如图1所示，R1为外圈内半径，R2为外圈外半径，T为厚度。含内部裂纹的轴承结构如图2所示，L为裂纹的长度，H2为宽度，H1为裂纹下表面距离轴承外圈内表面的距离，该裂纹为轴向内部裂纹。裂纹尖端区域有限元模型如图3所示。为准确描述裂纹特性，对裂纹尖端区域采用奇异单元进行离散。为简化有限元模型，假设轴承外圈为理想圆环结构，但要保证其弹性模量、密度、横截面积、截面惯性矩和中径半径与理论模型一致。为减少计算和提高计算精度，对正常外圈和含内部裂纹外圈的有限元模型采用高质量的四边形壳平面应变单元进行网格划分，以满足计算精度要求。轴承外圈整体有限元的单元总数为10 560，节点总数为11 220。球轴承外圈的两端面为自由端面或被刚性光滑面所固定，不发生纵向位移，采用二维平面应变单元对外圈建模[15]。

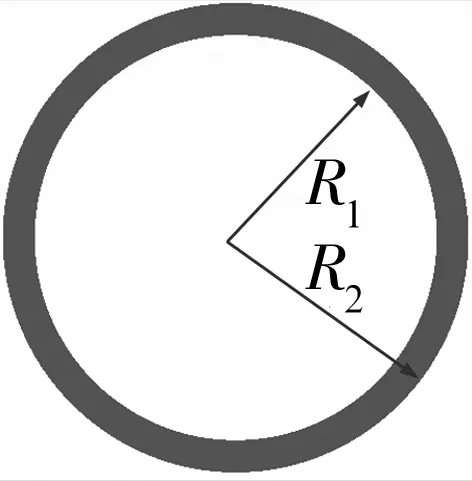
图1 正常轴承外圈

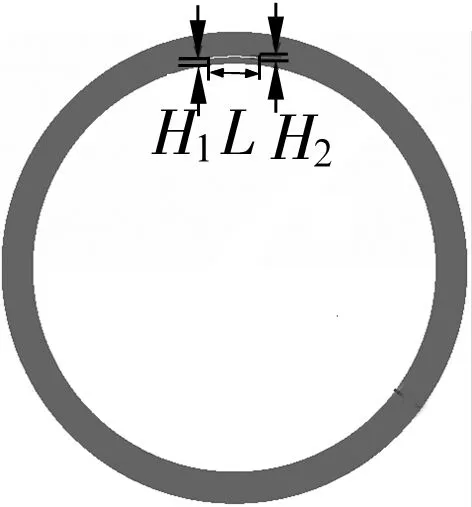
图2 含裂纹轴承外圈

图3 裂纹尖端模型

选取R1为62.5 mm，R2为72 mm，T为19 mm，L为8 mm，H2为0.3 mm，H1为1 mm。轴承外圈材料为GCr15钢，弹性模量为210 GPa，密度为7 800 kg/m3，泊松比为0.3。

3 结果与分析

通过有限元法对正常轴承外圈和含内部裂纹的轴承外圈进行自由模态分析[16]，提取前6阶固有频率和模态振型及其曲率进行分析。正常和含内部裂纹的轴承外圈固有频率见表1。通过(1)式得到轴承外圈的前6阶频率分别为2 610，7 300，13 230，20 670，29 896，39 670 Hz。由表1可以看出，有限元法和理论计算法计算基本一致，说明有限元法的模型正确。

由表1可知，内部裂纹使轴承外圈的前6阶固有频率减小，但减小幅度降低，仅通过固有频率的变化对外圈的内部裂纹进行诊断和识别比较困难。

表1 有限元分析结果

正常和含内部裂纹轴承外圈的前6阶模态振型分别如图4和图5所示。由图可知，内部裂纹对外圈模态振型的整体形态影响较小，由于裂纹区域局部刚度变化，在裂纹区域引起的局部模态变化较为明显。前6阶模态中，裂纹存在闭合和张开2种模态振型；第1，2和3阶，裂纹区域为闭合模态振型；第4，5和6阶，存在闭合和张开2种模态振型。

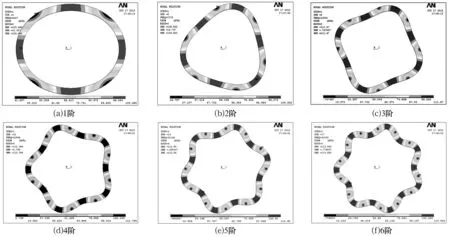
图4 正常轴承外圈模态振型

含内部裂纹轴承外圈前6阶模态振型曲率如图6所示,由图可知，正常轴承外圈模态振型曲率(曲线1)为光滑曲线，而含内部裂纹的轴承外圈模态振型曲率(曲线2)在裂纹区域存在明显的突变现象。内部裂纹会对外圈模态振型曲率产生较大的影响，且其影响区域即为裂纹所在的区域，故可通过诊断和识别外圈模态振型的曲率得到内部裂纹所在位置。

由于模态振型存在特殊节点，即振幅为0的节点，模态振型曲率可能出现对于特殊节点或其他影响而导致无突变的情况。内部裂纹长度对轴承外圈第4阶模态振动曲率的影响如图7所示。3种裂纹工况的高度和深度分别为0.3，1 mm。由图7可知，对于不同长度尺寸的内部裂纹，模态曲率方法也同样适用。

图5 含内部裂纹轴承外圈模态振型

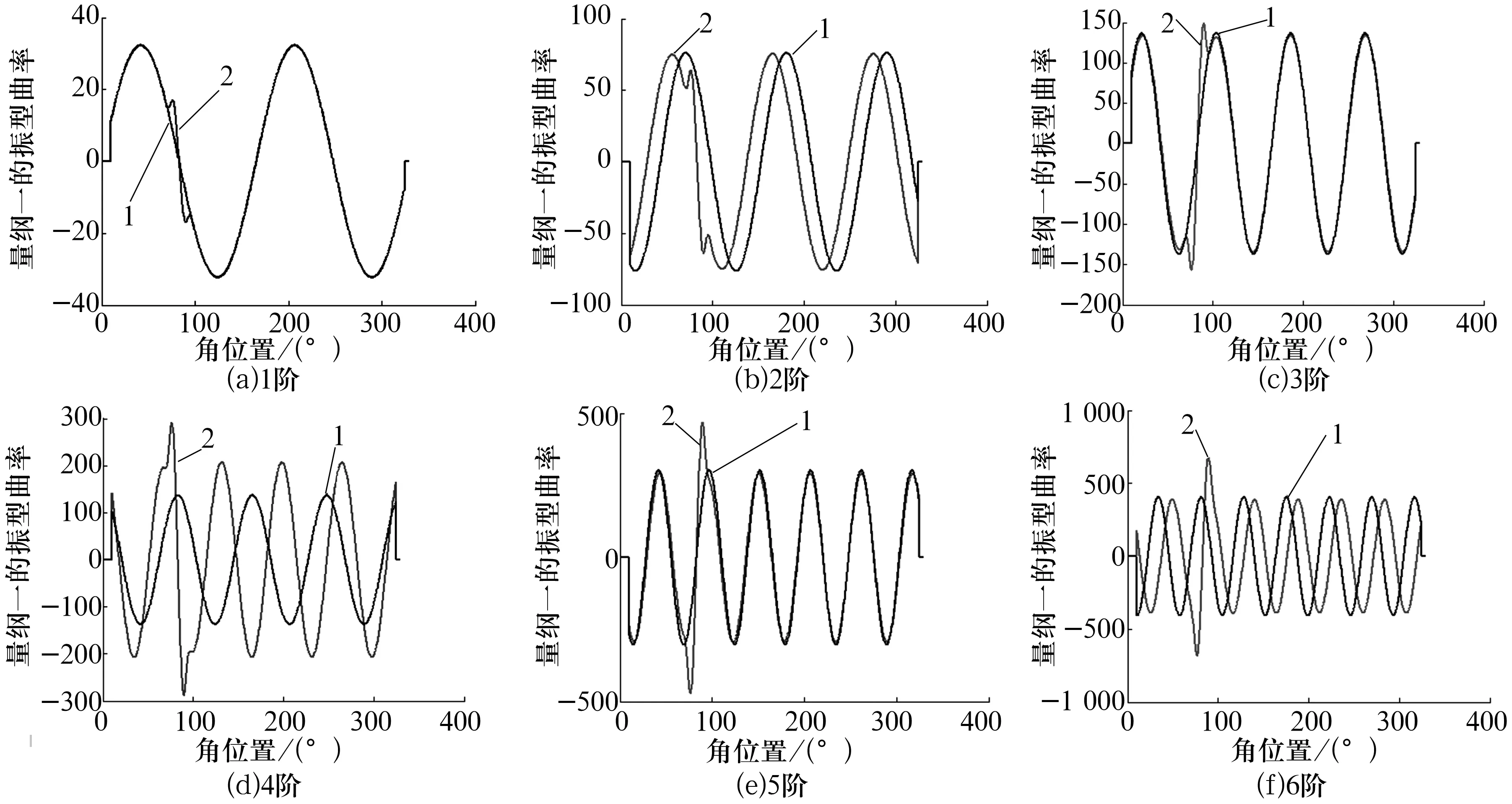
图6 轴承外圈模态振型曲率

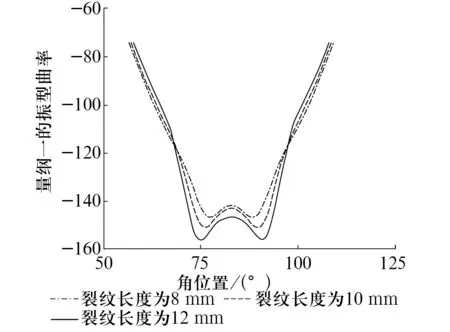
图7 内部裂纹长度对轴承外圈第4阶模态振型曲率的影响

4 结论

1)内部裂纹会使轴承外圈固有频率减小，但减小幅度较小；只采用固有频率的变化对外圈的内部裂纹进行诊断和识别比较困难。

2)内部裂纹对轴承外圈模态振型的整体形态影响较小，但在裂纹存在的区域引起的局部模态变化较为明显。

3)内部裂纹对外圈模态振型曲率有较大影响，影响区域即为裂纹所在区域，可通过分析外圈模态振型的曲率来诊断和识别内部裂纹所在位置。