形态学多尺度广义分形矩阵在轴承故障诊断中的应用
2017-07-25于忠德刘东升王锋李兵
于忠德,刘东升,王锋,李兵
(1.沈阳职业技术学院,沈阳 110000;2.军械工程学院 四系,石家庄 050003)
轴承的振动信号中包含了丰富的运行状态信息,而且能够在设备运转状态下采集,因此广泛采用振动信号对轴承进行故障分析与诊断[1-3]。大量研究表明,机械系统的振动信号具有较强的非线性特性,研究振动信号的非线性特征提取技术是轴承故障诊断的关键[4-6]。近年来,分形理论在很多涉及非线性分析的领域获得了广泛应用,在振动信号分析中的应用研究也取得了大量成果[7-9]。
分形理论对分析对象的一个重要假设是其具有严格的自相似性,但该性质在实际信号中很难满足。这种非严格自相似性体现在2个层面:1)空间分布上的非严格自相似性(也叫非均匀性),一般采用多重分形或广义分形维数理论处理;2)尺度上的非严格自相似性,可采用多尺度分形理论处理。然而,广义分形维数考虑了信号在空间分布上的非严格自相似性[8],但没有考虑信号在尺度上的非严格自相似性;多尺度分形考虑了信号在尺度上的非严格自相似性[10],但没有考虑信号在空间分布上的非均匀性。因此,提出采用多尺度广义分形矩阵表征轴承振动信号,同时考虑信号的空间非严格自相似性和尺度非严格自相似性,以对轴承振动信号的非线性特性进行更加全面和完整的表征。
目前,在信号分形维数估计中应用最广泛的方法是计盒法,但由于其采用了规则划分网格的特性,估计的分形维数有很大的不稳定性,因此,采用形态学覆盖法[8-9]估计轴承振动信号的分形维数,并进行对比验证。
1 形态学分形维数
1.1 数学形态学基本运算
腐蚀和膨胀是数学形态学的基本运算算子,其他数学形态学算子均以这2个基本算子为基础。由于文中只涉及一维振动信号的处理,因此仅给出腐蚀和膨胀在一维函数上的定义。
假设f(n)为定义在F={0,1,2,…,N-1}上的待分析信号,g(m)为定义在G={0,1,2,…,M-1}上的结构元素,其中N为信号点数,M为结构元素的点数,一般情况下N>>M,则f(n)关于g(m)的腐蚀和膨胀分别为
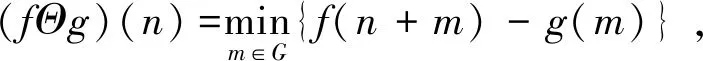
(1)
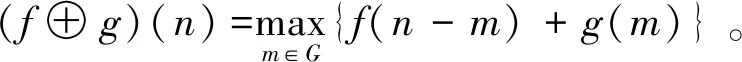
(2)
由以上公式可以看出,腐蚀运算相当于信号在一个滑动滤波窗内的最小值滤波,而膨胀运算相当于信号在滑动滤波窗内的最大值滤波,滑动滤波窗等价于结构元素[8-9]。
1.2 分形维数估计的形态学覆盖法
形态学覆盖法的基础就是前述的多尺度腐蚀和膨胀算子。与计盒法不同,形态学覆盖法计算的测度是腐蚀与膨胀之间的覆盖面积。假设分析尺度为ε,则该尺度下信号的测度为
(3)
εg=g⊕g⊕…⊕g。
根据已有研究,单位结构元素选为g={0,0,0},即长度为3的扁平结构元素,其优点是计算速度更快且不影响分形维数估计的精度。
分析信号的尺度定义为ε=1,2,…,εmax,最大分析尺度满足εmax≤N/2。根据分形测度理论,各尺度下的测度Ag(ε)应满足
(4)
对log(Ag(ε)/ε2)和log(1/ε)进行最小二乘拟合,估计的斜率DM即信号的形态学分形维数。
2 形态学多尺度广义分形矩阵
2.1 形态学广义分形维数
在形态学覆盖面积的基础上,可定义一个计算局部度量的分布函数ui(ε),即
(5)
(5)式中的f⊕εg(n)-fΘεg(n)反映的是信号膨胀与腐蚀间的差异,与计盒法相比,其作用相当于单个网格上盒子数,根据(5)式的定义,ui(ε)计算了这种差异的分布。而信号在空间上的不均匀性则通过分布函数高阶矩的奇异性得到了描述。
信号在尺度ε下的q阶度量定义为
(6)
由(5)式可发现,形态学覆盖法的网格划分是固定的,与尺度无关,均为分析信号的采样点数,即计盒法中尺度ε下的盒子个数N(ε)=N。与计盒法相比,形态学覆盖法中的Ag(ε)相当于盒数N(ε)与单位盒面积ε2的乘积,则
(7)
作为一个多重分形度量Kq(ε),与尺度之间必定满足的指数关系为
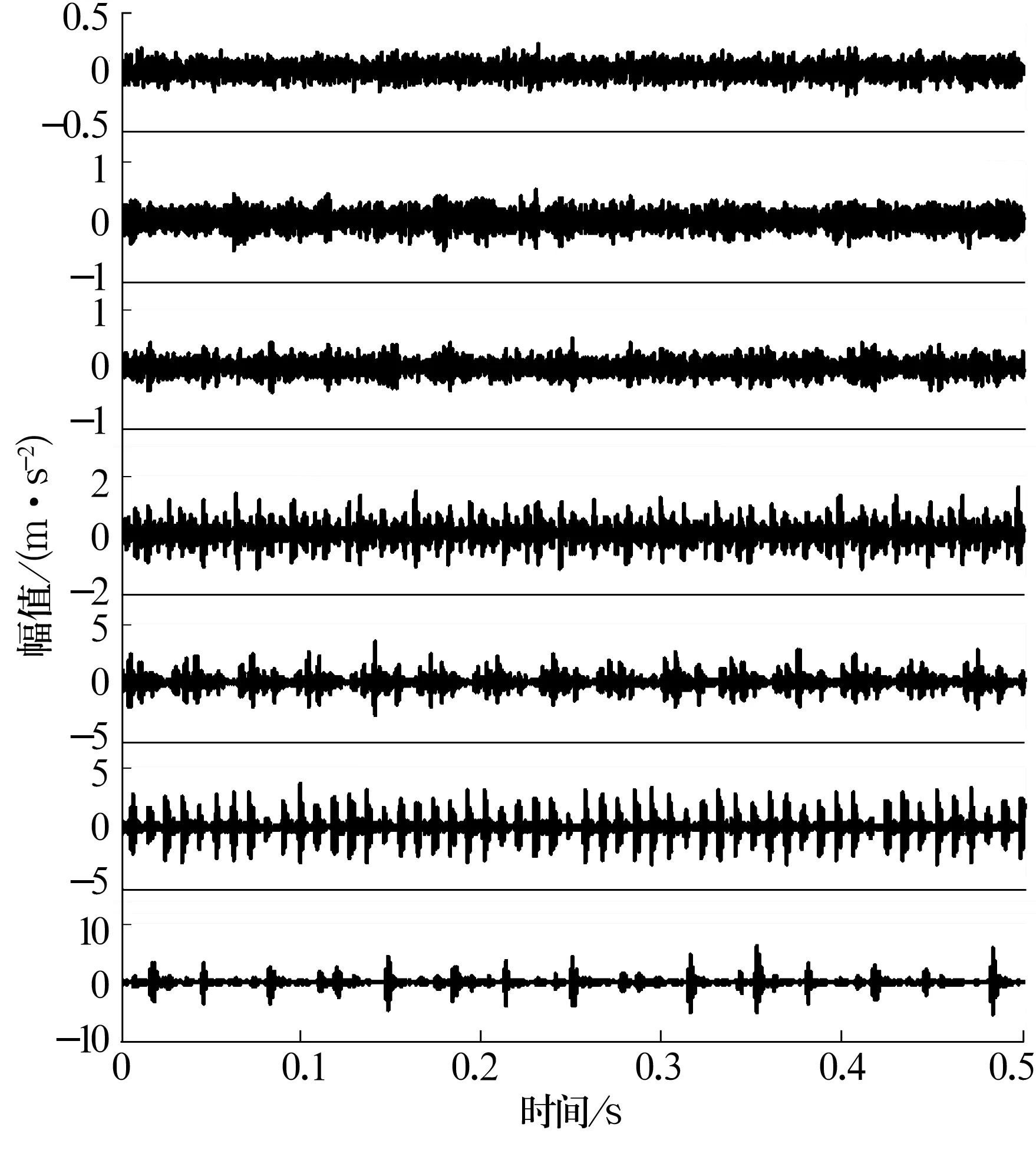
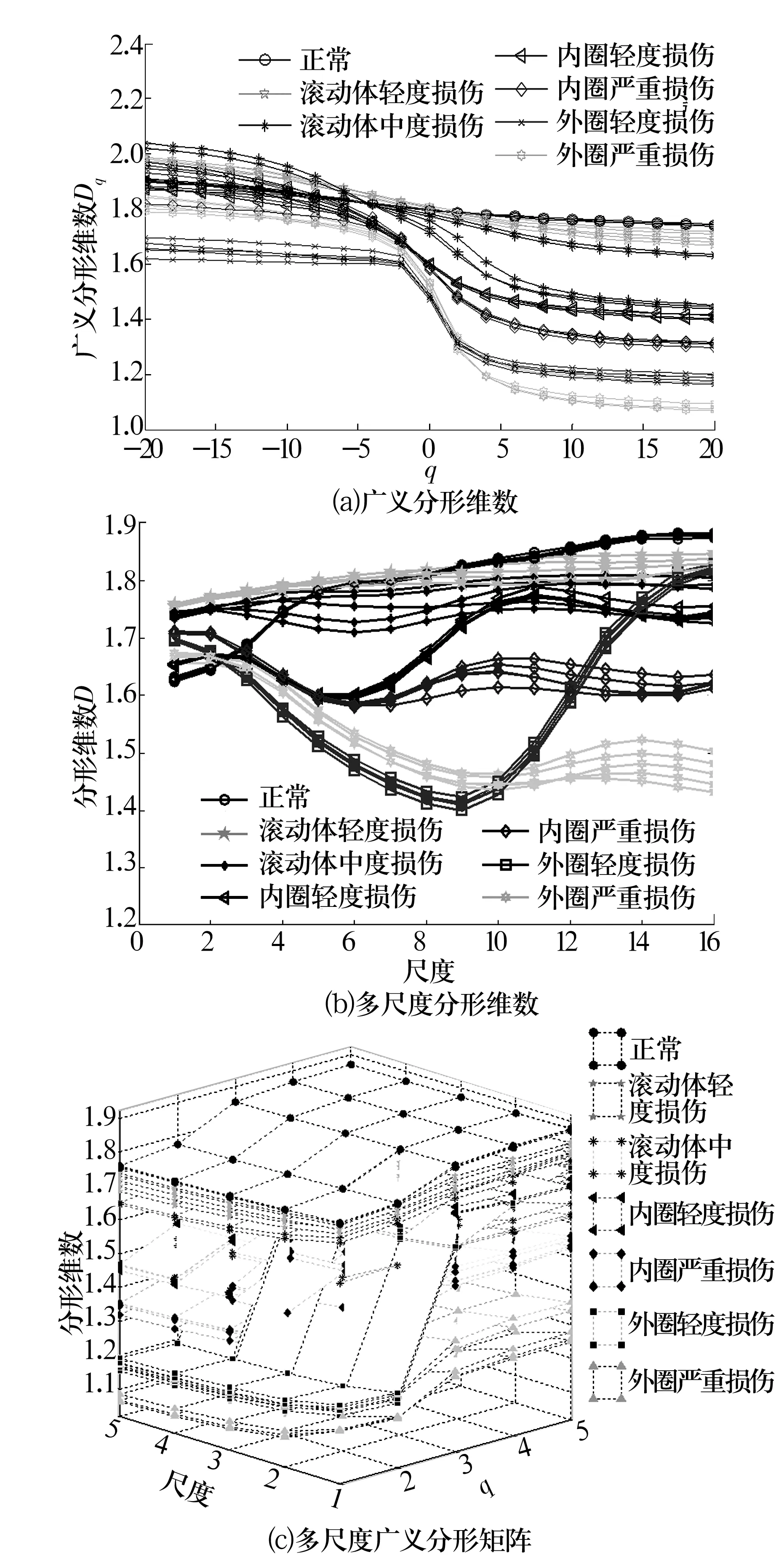
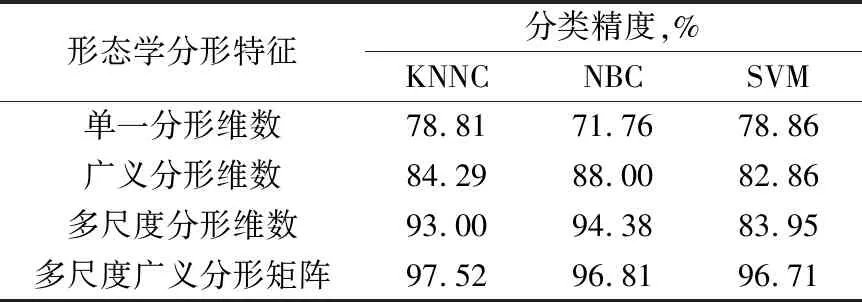
Kq(ε)∝ε-Dq;-∞ (8) 则基于数学形态学的多重分形维数为 (9) 实际计算中,对Kq(ε)和lnε进行最小二乘线性拟合得到对广义分形维数Dq的估计。可以证明:当q=0时,K0(ε)=-ln[Ag(ε)/ε2],则广义分形维数Dq退化为基于数学形态学的单一分形维数。 虽然广义分形维数反映了信号在空间上的非严格自相似性,但却不能反映信号在尺度上的非严格自相似性,而在现实中,在尺度上满足严格自相似的信号是不存在的,存在的只是在统计意义上的自相似。 如果待分析信号是严格自相似的,即满足尺度不变性,则在不同观测尺度下信号的分形维数是不变的;然而,轴承振动信号只满足统计意义的自相似,在不同观测尺度下,其分形维数存在一定的差异。因此,在形态学单一分形维数基础上,引入了形态学多尺度分形维数的计算方法[10]。 采用分段拟合的方式,其具体计算方法为:设分析信号的尺度为ε=[ε1,ε2,…,εL],则定义在局部尺度εi下的局部分形维数为[εi,εi+1,…,εi+w-1]窗内的最小二乘拟合值,其中w为窗的宽度值。从尺度ε1依次移动窗的位置,可以得到L-w+1个分形维数值。 轴承故障信号作为一种统计意义上的分形体,需要同时考虑其在空间和尺度上的非严格自相似性。因此,采用多尺度广义分形矩阵表征轴承故障信号。其主要思想为:在估计信号的广义分形维数时,在每一个参数q下,不再只估计其对应的单一全局分形维数,而是估计信号在各个局部尺度范围[εi,εi+1,…,εi+w-1]内的多个分形维数,即将原来每个q下的单一分形维数用多尺度分形维数代替,从而包含更加全面的信息。 为验证提出的形态学多尺度广义分形矩阵的有效性,采用实测的轴承故障信号计算各种分形维数并进行对比,轴承故障信号数据来自于美国Case Western Reserve University轴承数据中心[11]。试验轴承为SKF 6205,电动机转速为1 797 r/min,采样频率为12 kHz,采样点数为6 000。选择轴承正常状态及钢球、内圈、外圈的轻微(损伤直径0.178 mm)、严重(损伤直径0.533 mm)损伤共7种状态进行分析,7种状态下轴承振动信号的时域波形如图1所示。 图1 轴承7种状态下振动信号时域波形 采用形态学覆盖法计算各种分形维数,具体参数为:分析尺度ε=[1,2,4,8∶4∶72],共20个尺度;单位结构元素是长度为3的扁平结构元素;广义分形维数参数q选择为q=[-20∶2∶20];多尺度分形维数窗宽w选择为5。 轴承在不同状态下振动信号的形态学广义分形维数、多尺度分形维数及多尺度广义分形矩阵分别如图2所示,从图中可以看出: 图2 轴承不同状态下振动信号的形态学分布 1)在参数q<0时,形态学广义分形维数的分布十分混乱,不具有可分性;而在q>0时,相同状态下信号的形态学广义分形维数比较相近,具有一定的可分性,但是部分状态的形态学广义分形维数依然存在着一定的重叠区域。 2)形态学多尺度分形维数能够很好地区分轴承的7种状态,但在某些尺度下,轴承的各种状态之间依然存在部分的重叠。 3)形态学多尺度广义分形矩阵克服了前2种分形维数存在部分状态分形维数重叠的问题,能够更有效地区分轴承的7种状态。 为测试各种分形维数在轴承故障诊断中的效果,采用最近邻分类器(KNNC)、朴素贝叶斯分类器(NBC)和支持向量机分类器(SVM),采用上述的各种分形维数作为特征参数对轴承的7种状态进行分类。试验中,每种轴承状态采集20个样本(共140个样本),计算每个样本的各种形态学分形维数。然后在每种状态下随机选择10个样本作为训练样本,剩余样本作为测试样本。为保证结果的稳定和有效性,重复此随机选择过程50次并取平均值作为最终结果。 不同形态学分形维数在轴承振动信号中的分类精度见表1,由表可知:形态学多尺度广义分形矩阵在3种分类器上均获得了最高的识别率,说明其能够对轴承故障信号进行更全面和完整的表征,从而有效区分轴承的故障状态。 表1 各种分形维数的分类精度 针对轴承故障信号在空间分布与尺度分布上都具有非严格自相似性的特性,通过对形态学分形基本计算方法及广义分形维数和多尺度分形维数形态学覆盖计算方法的分析,引出了形态学多尺度广义分形矩阵的概念,并采用实测轴承故障信号对各种分形维数的故障分类效果进行了验证,试验结果表明,形态学多尺度广义分形矩阵能够对轴承振动信号进行更加全面的表征,提供更加丰富的故障诊断信息,从而获得较高的故障诊断精度。2.2 形态学多尺度分形维数
2.3 多尺度广义分形矩阵
3 轴承故障信号分析
4 结束语
