球环分隔式角接触球轴承游隙与偏差

刘建志，黄振，祁百龙

(常州东风轴承有限公司，江苏 常州 213022)

符号说明

Bi——内圈两沟道中心距

ΔBi——Bi的偏差

Ce——承载球与外沟道接触点所在径向平面到外圈窄端面的距离

ΔCe——Ce的偏差

d——轴承内径

do——与轴承内圈配合轴的内孔直径(空心轴内径)

di——内沟道直径

Δdi——di的偏差

Dk——轴承座直径

D——轴承外径

De——外沟道直径

ΔDe——De的偏差

Dw——承载球球径

ΔDw——Dw的偏差

Dbw——分隔球球径

ΔDbw——Dbw的偏差

Dbe——保持环沟底直径

Dfw——分隔球组外接圆直径

ΔDfw——Dfw的偏差

fi，fe——内、外沟曲率半径系数

Δfe——外圈与轴承座配合的过盈量

Δfi——内圈与轴配合的过盈量

Gaoj——内外圈沟径偏差和承载球球径偏差引起轴向游隙的变化量

Groj——内外圈沟径偏差和承载球球径偏差引起径向游隙的变化量

Gaoz——内外沟道距离偏差引起轴向游隙的变化量

Grou——分隔球组与保持环沟道过盈配合量引起径向游隙的变化量

Gaou——分隔球组与保持环沟道过盈配合量引起轴向游隙的变化量

Gau——轴承安装后内沟道膨胀量和外沟道收缩量引起轴向游隙的变化量

Gru——轴承安装后内沟道膨胀量和外沟道收缩量引起径向游隙的变化量

Gaz——轴承安装后的轴向工作游隙

Gao——轴承初始轴向游隙

Kf——与承载球球径和内外圈沟曲率半径系数有关的常数

Lx——同列相邻两承载球球心的周向距离

ΔLx——Lx的偏差

Ly——两列承载球组中心距

ΔLy——Ly的偏差

ΔLyu——分隔球组与保持环沟道过盈配合量引起Ly的变化量

M——与分隔球相切的4个承载球球心所在平面到轴承轴线的2倍距离(承载球平面距离)

ΔM——M的偏差

ΔMu——轴承安装后内沟道膨胀量和外沟道收缩量引起承载球平面距离的变化量

N——分隔球球心到4承载球球心平面距离的两倍(分隔球球心距离)

ΔN——N的偏差

ΔN1——承载球和分隔球球径偏差引起分隔球球心距离的偏差

ΔN2——内外圈沟径偏差引起分隔球球心距离偏差

ΔN3——两列承载球中心距离偏差引起分隔球球心距偏差

ΔN2u——轴承安装后内沟道膨胀量和外沟道收缩量引起分隔球球心距的变化量

Ufb——分隔球组与保持环沟道过盈配合量

Ufi——内沟道膨胀量

Ufe——外沟道收缩量

Z——单列承载球数或分隔球数

αi，αe——承载球与内、外沟道接触角

下标

+——上偏差

-——下偏差

max——最大

min——最小

1 游隙与偏差的意义

一般球轴承初始游隙的取值与主机要求的工作游隙及内外圈与轴、轴承座配合后沟道直径的变化量有关，其主要受内外圈沟径偏差和球径偏差的影响。球环分隔式双列角接触球轴承如图1所示，该类轴承初始游隙还受内外沟道距离、分隔球组外接圆直径和保持环沟道过盈配合量的影响，初始游隙的计算方法复杂。

图1 球环分隔式角接触球轴承

球环分隔式双列角接触球轴承安装后，内外沟道直径的变化不仅会引起轴承游隙变化，还会引起分隔球组外接圆直径变化，从而改变分隔球组与保持环沟道的接触状态以及分隔球与承载球、承载球与内、外沟道的接触状态。故需要分析内、外沟道变化量对轴承游隙和分隔球组外接圆直径的影响，以便确定合理的保持环沟径偏差。

球环分隔式双列角接触球轴承零件较多，影响轴承游隙和分隔球组外接圆直径的因素多，各零件相互关系复杂，为得到符合主机要求的产品，需分析轴承游隙与零件尺寸偏差的关系，得到缩小轴承初始游隙公差和分隔球组外接圆直径公差方法。

2 游隙与沟径偏差、球径偏差的关系

角接触球轴承的径向游隙与沟径偏差、球径偏差的关系如图2所示， 球环分隔式双列角接触球轴承内外圈沟径和承载球球径对轴承径向游隙的影响与常规角接触球轴承相同。

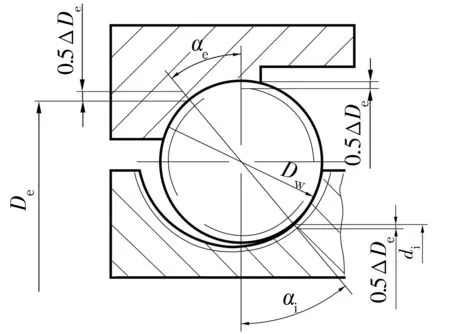
图2 径向游隙与沟径偏差、球径偏差位置关系

一般情况下承载球与内外沟道接触角相等，即

αe=αi=α,

(1)

由几何关系得

Groj=ΔDe-Δdi-2ΔDwcosα。

(2)

角接触球轴承轴向游隙测量方法简单，故常将径向游隙转化为轴向游隙测量。轴向游隙与径向游隙的关系为[1]

(3)

Kf=(fi+fe-1)Dw。

3 游隙与内外沟道距离偏差的关系

轴向游隙与内外沟道距离偏差的位置关系如图3所示，则

Gaoz=ΔCe1+ΔCe2-ΔBi。

(4)

图3 轴向游隙与内外沟道距离偏差的位置关系

在工艺上可使ΔCe1和ΔCe2相等，(4)式可转化为

Gaoz=2ΔCe-ΔBi，

(5)

当2ΔCe-ΔBi≥0时，轴向游隙增大；当2ΔCe-ΔBi≤0时，轴向游隙减少。

4 分隔球组外接圆直径偏差

为确定合理的保持环沟径偏差，讨论分隔球组与保持环的过盈配合对轴承游隙的影响，需计算分隔球组外接圆直径偏差。与分隔球组外接圆直径相关的量较多，为简化计算，采用微分分析法。保持环沟道直径为[2]

Dbe=M+N+Dbw。

(6)

分隔球组外接圆直径与保持环沟道直径相同，但偏差大小和方向不同，为避免混淆，分隔球组外接圆直径用Dfw表示，即

Dfw=M+N+Dbw，

(7)

M=Dpwcosφ，

(8)

(9)

Lx=Dpwsinφ，

(10)

(11)

式中：Dpw为球组节圆直径。

不考虑αe和αi的误差对分隔球外接圆直径的影响，由(1)，(11)式得

(12)

对(7)～(10)，(12)式微分得

dDfw=dM+dN+dDbw，

(13)

dM=dDpwcosφ，

(14)

dN=[(Dw+Dbw)(dDw+dDbw)-

LxdLx-LydLy]N-1，

(15)

dLx=dDpwsinφ，

(16)

(17)

将(17)式代入(14)和(16)式得

(18)

(19)

(19)式代入(15)式得

dN=[(Dw+Dbw)(dDw+dDbw)-

0.5Dpw(dDe+ddi)sin2φ+LydLy]N-1。

(20)

将(13)，(18)，(20)式中的微分用偏差替代得

ΔDfw=ΔM+ΔN+ΔDbw，

(21)

(22)

ΔN=ΔN1-ΔN2-ΔN3，

(23)

(24)

(25)

(26)

由(22)式可知，ΔM仅与内外圈沟径偏差有关。ΔN不仅与内外圈沟径偏差有关，还与承载球球径和分隔球球径偏差及两列承载球中心距偏差有关，ΔN对分隔球组外接圆直径偏差的影响较大。

由(24)～(26)式可以看出，组配轴承时，若承载球球径偏差和分隔球球径偏差符号相反时， ΔN1变小，若两者数值相等， ΔN1为0。ΔN2较小,ΔN3对分隔球球心偏差影响较大。

ΔLy与ΔBi的关系为

ΔLy=ΔBi+ΔDwcosα，

(27)

从(27)式可以看出，ΔBi不仅影响游隙公差，还影响分隔球组外接圆直径。

计算ΔDfw时，各偏差的大小和方向必须与计算轴承游隙时的值保持一致。通过实例计算得到最佳组合状态下ΔDfw的上下偏差为

ΔDfw+=ΔM-+ΔNsz-+ΔDbw-，

(28)

ΔDfw-=ΔM++ΔNxz++ΔDbw+，

(29)

(30)

(31)

ΔNsz-=ΔN1z--ΔN2--ΔN3-，

(32)

ΔNxz+=ΔN1z+-ΔN2+-ΔN3+，

(33)

(34)

(36)

(37)

(38)

(39)

将(35)，(37)，(39)式代入(31)式得

ΔNsz-=[(Dw+Dbw)(ΔDw++ΔDbw-)-

0.5(ΔDe-+Δdi-)sin2φ+LyΔLy-]N-1，

(40)

(34)，(36)，(38)式代入(32)式得

ΔNxz-=[(Dw+Dbw)(ΔDw-+ΔDbw+)-

0.5(ΔDe++Δdi+)sin2φ-LyΔLy+]N-1。

(41)

由(40)，(41)式可知,ΔDe和Δdi方向相同，与后文中游隙偏差方向一致，且承载球和分隔球的偏差方向相反，故(40)，(41)式是使ΔDfw获得最小范围的组配。

5 分隔球组与保持环配合对游隙的影响

当分隔球组与保持环为间隙配合时，保持环和分隔球仅有分隔承载球作用；当分隔球组与保持环为过盈配合时，保持环和分隔球有分隔承载球和微量补偿调节轴承游隙或对轴承适度预紧的作用。

当分隔球组与保持环过盈配合时，保持环有向外膨胀的趋势，保持环在内应力的作用下有向内回复的趋势，存在向内的回复力。回复力通过分隔球传递给承载球，保持环和分隔球对轴承游隙的补偿或调节作用如图4所示，P为分隔球对每个承载球作用力的合力，βg为分隔球与承载球的切向角在轴向剖面上的投影。若轴承中存在径向游隙Gre和径向游隙Gri,在力P作用下，承载球移动，承载球和内外沟道始终接触。由此可知，保持环的回复力能够微量调节轴承游隙或对轴承适度预紧。

图4 保持环和分隔球对轴承的游隙补偿或预紧示意图

根据工况条件，确定分隔球组与保持环沟道的配合形式。间隙配合对轴承游隙无影响，仅分析过盈配合对轴承游隙的影响。

若Dbe

Ufb=Dfw-Dbe,

(42)

若不考虑保持环向外的膨胀量，保持环压迫分隔球，其外接圆直径缩小量ΔDfw=Ufb，代入(21)式得

Ufb=ΔM+ΔN+ΔDbw。

(43)

轴承组装后零件尺寸偏差不变，仅ΔN3改变，即

(44)

由(44)式得

(45)

ΔLy为两列球中心距偏差与分隔球外接圆直径偏差的关系; ΔLyu为过盈量Ufb引起两列承载球中心距的变化量。

从图4可以看出，当承载球球心从O移到O′时，外圈接触角变大，内圈接触角变小，变化量较小，故忽略接触角的影响。为避免接触角给轴承运动带来不利影响，较大的轴承游隙通过调整内外圈沟径偏差和沟道距离偏差来补偿，微量补偿轴承游隙或对轴承适度预紧可通过调整分隔球组与保持环的过盈量实现。

同(5)式， ΔLyu使轴向游隙减少量为

(46)

从(46)式可以看出，Ufb较小，Ly比N大，故Gaou较小，这就是微量补偿调节轴承游隙和对轴承适度预紧的原理。

6 轴承安装过盈量对轴承游隙的影响

内沟道膨胀了Ufi，即内沟道增加了一个直径偏差Δdi=Ufi；外沟道收缩了Ufe，即外沟道减少了一个直径偏差ΔDe=Ufe。内沟道膨胀和外沟道收缩使轴承径向游隙减少，即

Gru=Ufi+Ufe，

(47)

则轴向游隙的减少量为

(48)

7 轴承安装过盈量对分隔球外接圆直径的影响

分隔球组外接圆直径偏差与承载球中心圆直径和内外圈沟径偏差有关，用Ufi和-Ufe替换(22)和(25)式中的Δdi和ΔDe，即

(49)

(50)

分隔球组外接圆直径的变化量为

ΔDfwu=ΔMu+ΔN2u。

(51)

为使(47)和(48)式中的Ufi和Ufe的符号统一，在(49)和(50)式中Ufe前加负号。在(51)式中，若ΔDfwu≥0，分隔球组外接圆直径增大；若ΔDfwu≤0，分隔球组外接圆直径减少。(49)和(50)式忽略了接触角的影响，但满足需求。

分隔球组外接圆直径的变化会改变分隔球组与保持环的配合状态。分隔球组与保持环的过盈量Ufb会引起轴承游隙的变化， ΔDfwu也会引起轴承游隙的变化， ΔDfwu较小，通过(49)～(51)式可计算出ΔDfwu，将ΔDfwu当作Ufb的一部分来计算ΔDfwu对轴承游隙的影响。

8 初始轴向游隙的计算

轴承工作游隙与载荷、转速、温度、旋转精度等条件有关。角接触球轴承一般讨论轴向游隙，故仅讨论初始轴向游隙的计算方法。轴承初始轴向游隙的最大值和最小值分别为

Gao max=Gaz max+Gau max，

(52)

Gao min=Gaz min+Gau min。

(53)

由(48)式得

(54)

(55)

通过文献[3]计算Ufi max，Ufe max时，取最大过盈量Δfi max，Δfe max；计算Ufi min，Ufe min时，取最小过盈量Δfi min，Δfe min。

将(54)式代入(52)式得

(56)

将(55)式代入(53)式得

(57)

内外圈沟径偏差和承载球球径偏差引起轴向游隙的变化量为Gaoj，内外沟道距离偏差引起轴向游隙的变化量为Gaoz，分隔球组与保持环的过盈量引起轴向游隙的减少量为Gaou。轴向游隙在Gao max和Gao min之间，则

Gao max=Gaoj max+Gaoz max+Gaou max，

(58)

Gao min=Gaoj min+Gaoz min+Gaou min，

(59)

由(2)，(3)式得

(60)

(61)

由(5)式可得

Gaoz max=2ΔCe+-ΔBi-，

(62)

Gaoz min=2ΔCe--ΔBi+，

(63)

由(46)式得

(64)

(65)

将(60)，(62)，(65)式代入(57)式得

(66)

将(60)，(62)，(64)式代入(61)式得

(67)

(66)和(67)式中的ΔDe，Δdi，ΔDw的上下偏差与(30)，(31)，(40)，(41)式中的上下偏差一致，故该组配方式符合逻辑。

联立(51)，(57)式得

Gaoj max+Gaoz max+Gaou max=Gaz max+Gau max，

(68)

联立(53),(59)式得

Gaoj min+Gaoz min+Gaou min=Gaz min+Gau min。

(69)

在(68)，(69)式中，等式右边为轴承的轴向游隙规范，等式左边是：为满足轴承的轴向游隙规范，零件尺寸偏差和分隔球组与保持环的过盈量如何选择。为满足(68)，(69)式，等式左边的量要多次计算，分隔球组与保持环过盈量对轴承的径向游隙影响很小，初步计算时暂不考虑，各偏差确定后再考虑。

9 结束语

针对球环分隔式角接触球轴承的结构特点和工作特性，分析了球环分隔式双列角接触球轴承各零件相关尺寸偏差以及分隔球组和保持环沟道的过盈配合量与轴承游隙的关系,讨论了轴承安装后的内沟道膨胀量和外沟道收缩量对轴承工作游隙和分隔球组外接圆直径的影响，并给出了分隔球组外接圆直径偏差与相关零件偏差的关系。虽对球环分隔式角接触球轴承的游隙与偏差关系等进行了分析和计算，但保持环沟道外膨胀量、轴承各零件变位、内外沟曲率偏差、温度的影响还未考虑到，有待进一步研究。