某型圆锥滚子轴承保持架断裂仿真分析

王宇石，邱宝象，铁晓艳，张振潮,4，曾献智

(1.中国航发哈尔滨轴承有限公司 研发中心，哈尔滨 150025；2.万向钱潮股份有限公司，杭州 311215；3.洛阳轴研科技股份有限公司，河南 洛阳 471039；4.河南科技大学，河南 洛阳 471003)

轨道车辆轴箱用圆锥滚子轴承为重要支承件，目前对圆锥滚子轴承的研究较侧重于轴承的应力变化规律和承受载荷大小，对保持架的分析较少。某型轻轨机车在12万公里左右更换润滑油时发现圆锥滚子轴承失效，拆解检查发现部分齿轮箱配套圆锥滚子轴承保持架发生断裂(共配套400多套轴承，失效件30套)。基于此，对圆锥滚子轴承保持架断裂进行失效分析。

1 工况条件

失效轴承为主动轴上的一对圆锥滚子轴承，运行中轴承承受齿轮啮合力的反作用力以及振动加速度引起的冲击载荷。齿轮啮合力的反作用力随斜齿轮的螺旋角和旋转方向而改变方向，振动加速度引起的冲击载荷分为上下、左右、前后方向，大齿轮、小齿轮均在轴承作用点上承受载荷。齿轮啮合力的反作用力和振动加速度可转换为承载区域的合成径向载荷和合成轴向载荷，合成载荷通过内圈大挡边，经滚子传递至外圈，故内圈大挡边压在滚子大端面，小挡边不承受载荷。齿轮箱轴承结构如图1所示，图中各符号的含义及参数值见表1。

图1 齿轮箱轴承结构简图

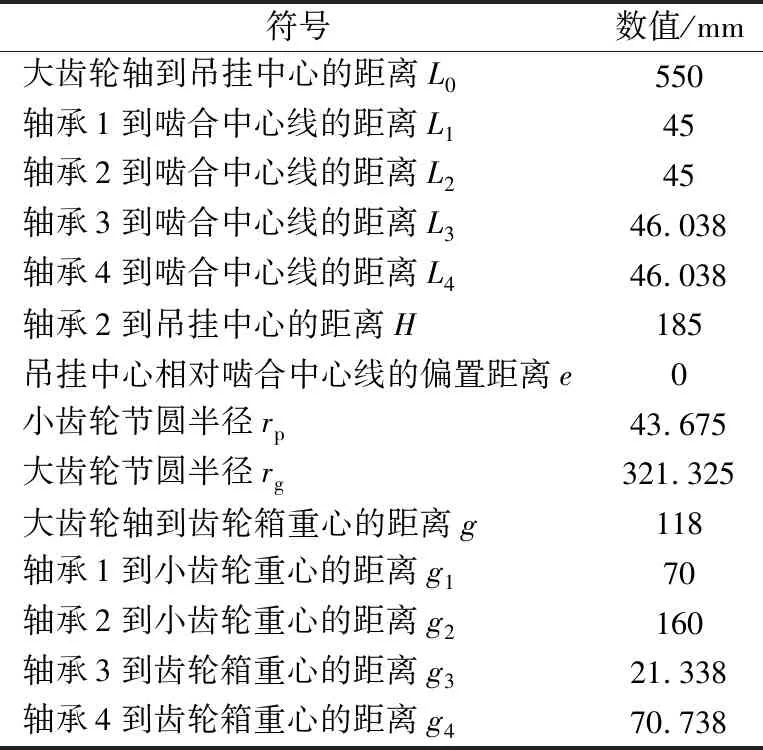
表1 图1中符号说明表

2 轴承载荷计算

保持架理论情况下处于悬浮不受力状态，但实际工作中，由于振动、润滑不均、滚子歪斜等因素造成保持架的非正常受力，所以在对保持架进行受力分析前有必要对轴承的工作载荷进行分析。

2.1 接触应力计算

已知轴承工作温度为60～80 ℃，转速为2 580 r/min，设输入扭矩为705 N·m，选取31315标准圆锥滚子轴承面对面安装，根据运转时轴承受载工况(图2)，并考虑小齿轮自重以及振动的影响，可计算出失效轴承(输入端轴承31315)理论状态下的载荷情况(表2)[1-2]。

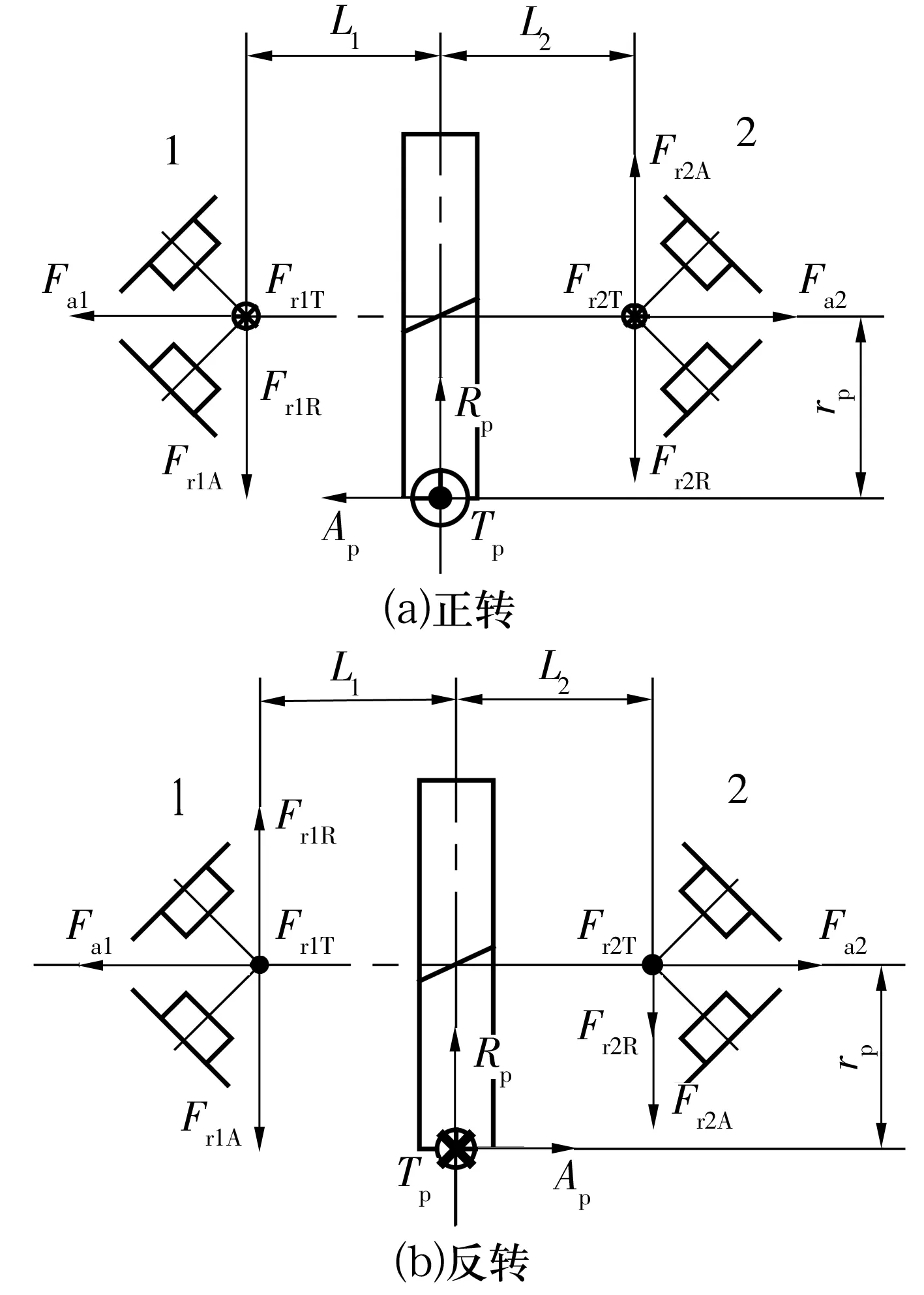
图2 运转时轴承受力分析

图2、表2中：M为额定工况时齿轮轴转矩；Tp为小齿轮切向分力；Rp为小齿轮径向分力；Ap为小齿轮轴向分力；FrT为切线方向分力产生的径向载荷；FrR为径向分力产生的径向载荷；FrA为轴向分力产生的径向载荷；Fa为轴向分力产生的轴向载荷；FaA为轴向分力产生的轴向载荷；FaR为派生轴向载荷；FrV为上下方向振动载荷；FrH为前后方向振动载荷；FaL为左右方向振动载荷；FR为合成径向载荷；FA为合成轴向载荷；Pr为等价径向载荷。

表2 输入端轴承理论状态下载荷

根据表2中正转时轴承1载荷条件(径向载荷15.53 kN、轴向载荷13.09 kN)，采用CobraAhs 6.1软件进行计算，得到轴承内部载荷分布结果(表3)。

表3 正转时轴承1的载荷和应力分布

根据以上载荷分布及应力计算结果可知，正向旋转时轴承1所含的16粒滚子全部承载，且最大接触应力极值均远小于许用接触应力值4 000 MPa，满足使用要求。此时所有滚子及保持架的公转角速度相同，滚子与保持架弹性拖动力及阻尼力均为零，即滚子与保持架间的作用力很微小，可以忽略。

当反向旋转时，由表2可知，此时轴承1仅承受径向载荷13.67 kN，同样采用CobraAhs 6.1软件进行计算，得到轴承内部载荷分布结果见表4。

表4 反转时轴承1的载荷和应力分布

根据以上载荷分布及应力计算结果可知，反向旋转时只有5粒滚子承载，最大接触应力极值仍远小于许用接触应力值4 000 MPa，满足使用要求。

2.2 保持架载荷

保持架理论上是一个绕轴承轴线做定轴转动的非受力零件，轴承的载荷由轴承内部(内外滚道面、内圈大挡边面、滚子滚动面和端面)承受，不直接作用于保持架。实际工作中，保持架不仅承受滚子对其的碰撞力和摩擦力，引导套圈对其的法向力和摩擦力，还承受质量不平衡力、重力和离心力等[3]。将保持架受力分为两部分：一部分是稳态作用力，由滚子与保持架兜孔接触后引起的作用力和滚子与保持架兜孔之间的流体作用力组成；另一部分是瞬态作用，由保持架的转速与滚子的公转角速度不一致而引起的碰撞力和阻尼力组成[4]。根据圆锥滚子轴承工况条件，保持架仅承受由振动加速度引起的滚子对保持架兜孔的撞击力FCP，即瞬态作用力，如图3所示。

图3 保持架承受滚子冲击力

由于滚子与保持架的瞬态作用力有时会导致保持架的加速旋转，有时会导致保持架的减速旋转，因此，此作用力可以看作一个模糊的计算量。根据文献[5]的基本理论，运用存在相对间隙的碰撞副模型，建立滚子与保持架相互作用的等价瞬态动力学模型，如图4所示。

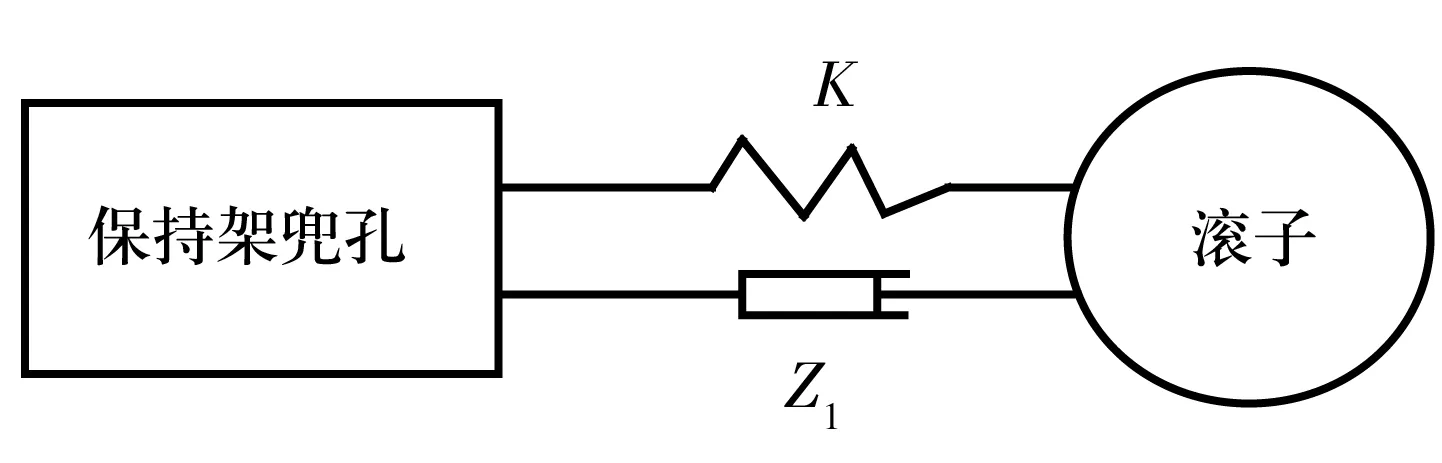
图4 滚子与保持架相互作用的等价瞬态动力学模型

根据该模型，由Hertz公式的变化模型[4]可以得到滚子对保持架的作用力为

FCP=ΔF+Fz=kδ+Z1V，

(1)

式中：ΔF为承载区滚子对保持架的弹性碰撞力，即拖动力；Fz为滚子与保持架兜孔之间的阻尼力；k为间隙碰撞弹性系数；δ为滚子与保持架的相对位移；Z1为滚子与保持架间隙碰撞副黏滞阻尼系数；V为滚子与保持架相对线速度；L为滚子长度；νg，νc分别为滚子和保持架的泊松比；Eg，Ec分别为滚子和保持架的弹性模量；ωg为滚子公转角速度；ωc为保持架角速度；Dpw为滚子组节圆直径；Δt为碰撞时间。

3 保持架断裂失效分析

根据保持架的失效照片(图5)可知，保持架失效形式为滚子端面接触区域明显磨损和窗孔圆角位置发生断裂。圆锥滚子轴承工作过程中振动、滚子歪斜以及滚子非正常接触载荷是导致保持架破坏的主要因素。结合已知失效形式，从保持架模态分析和结构强度2方面进行保持架的断裂分析[6]。

图5 保持架失效形式

3.1 模态分析

31315圆锥滚子轴承保持架结构参数如图6所示，使用Solidworks建立三维实体建模，然后导入ABUQUS进行模态分析(图7)。表5为计算该保持架前10阶的固有频率，其中前6阶为平动模式，频率均为极小值。第7～10阶振型如图8所示。

图6 轴承保持架结构参数

图7 保持架模态分析有限元模型

表5 保持架模态分析结果

图8 保持架7～10阶振型

根据以上分析结果，按照极限转速4 650 r/min进行理论计算，可知其传递载荷频率为1 085 Hz，远低于7阶频率值7 158.9 Hz，因此，可排除共振导致保持架失效的因素。

3.2 结构有限元分析

根据轴承工况条件可知，圆锥滚子轴承处于弯矩作用下，内圈会随着轴的翘曲发生微小的倾斜，滚子发生歪斜，从而导致滚子与滚道接触区域向大端趋近(图9)，同时滚子倾斜与兜孔小端面接触并产生相对摩擦(图10)。因此，结构分析的重点在于通过有限元模型模拟保持架大端面和小端面承受滚子接触载荷时的应力分布，并寻找容易发生失效的结构薄弱点[7-8]。主要从3方面入手：1)滚子与保持架兜孔小端不接触；2)滚子与保持架兜孔小端接触；3)保持架兜孔圆角半径的影响。

图9 失效轴承滚子大端接触痕迹

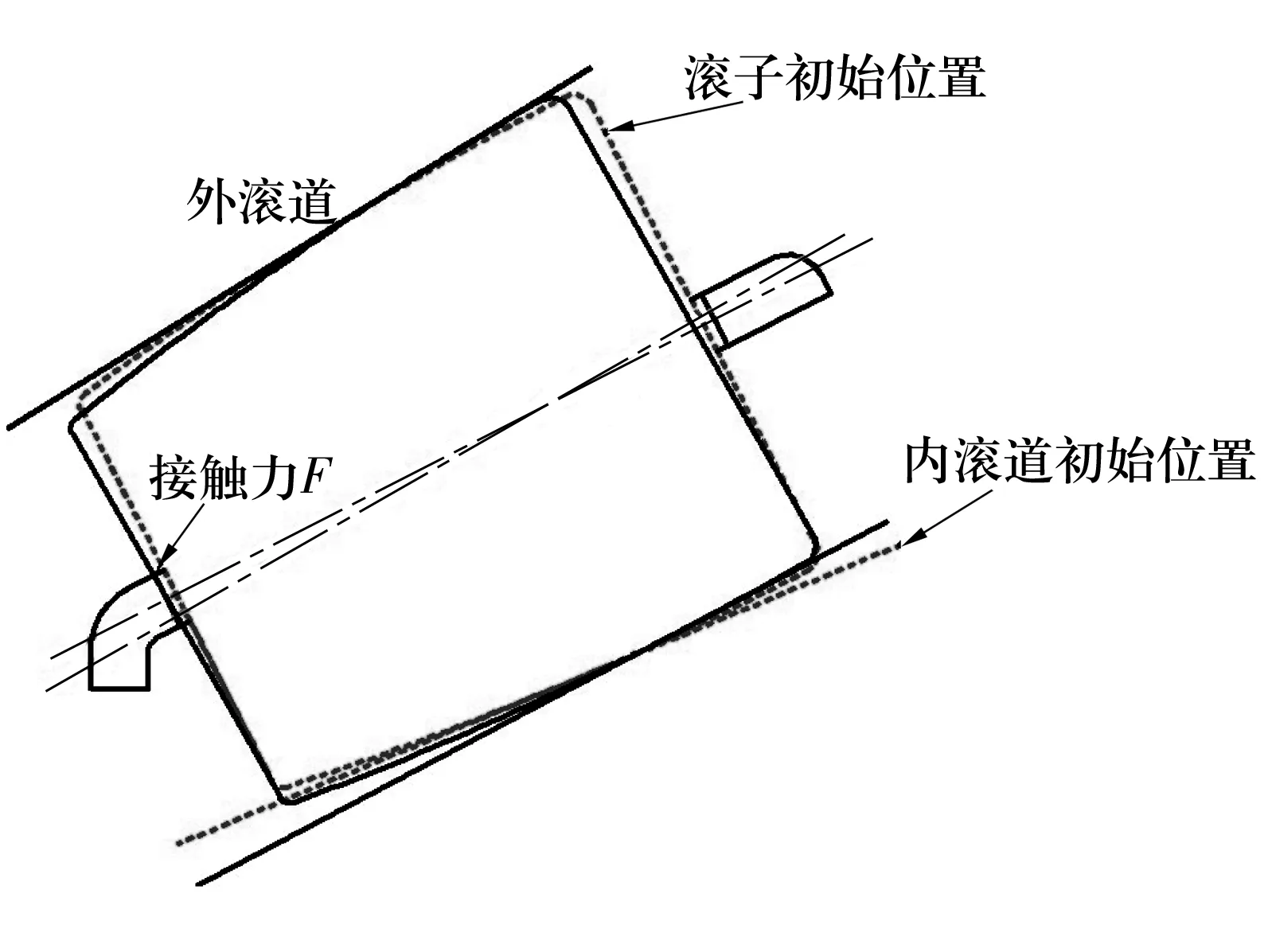
图10 滚子倾斜与保持架接触示意图

根据保持架的结构圆周均布的特点，在原有完整保持架模型的基础上建立单兜孔局部模型，并通过在延伸边梁截面上施加位移约束来模拟保持架剩余部分对其刚性约束(图11)。

图11 单兜孔保持架模型

3.2.1 滚子与保持架兜孔小端不接触

内、外圈同轴，滚子与保持架兜孔小端不接触条件下，保持架仅承受滚子沿圆周切线方向的拖动力。模型中兜孔圆角为R0.5 mm，材料选用10#碳钢，弹性模量为2.1 GPa，泊松比0.28，屈服强度220.6 MPa。约束、载荷条件如图12所示。根据计算结果，当拖动力达到417.5 N时，等效应力极值达到220.6 MPa，超出了材料的屈服强度值，此时应力集中位置主要位于受载过梁的小端圆角内侧和大端圆角外侧，如图13所示。

图13 仅施加圆周切线拖动力时应力分布

3.2.2 滚子与保持架兜孔小端接触

当滚子与保持架小端发生接触后，由于接触载荷与相对旋转运动的影响，会导致产生磨损痕迹(图5)。在模型中，对兜孔小端施加法向压力载荷以模拟滚子的接触作用，约束及载荷条件如图14所示。为便于比较，仍施加周向拖动力417.5 N。当兜孔小端法向压力载荷分别为100，200，300 N时，等效应力极值相应分别增大至251.0，289.6，336.3 MPa(图15)，应力集中位置仍保持不变，但小端圆角处应力极值增幅明显大于大端。

图14 约束及载荷条件

图15 不同兜孔小端载荷下的应力分布

3.2.3 圆角半径影响

兜孔圆角处易产生明显的应力集中并导致断裂失效[9]，为进一步分析圆角尺寸对保持架应力集中的影响，设定拖动力载荷200 N，小端接触载荷200 N条件下，调整模型中兜孔圆角半径，得到等效应力分布如图16所示。由图可知，当圆角半径为0.2，0.3，0.4，0.5 mm时，对应兜孔等效应力极值分别为228.1，209.7，184.4，175.1 MPa，变化比例达30%。

4 结论

通过对31315型圆锥滚子轴承保持架断裂失效形式进行分析和有限元仿真，可知：

1)齿轮箱传动轴刚度不足，导致弯矩作用下轴承内、外圈不同轴，进而引起滚子倾斜并与保持架兜孔小端产生接触压力，这可能是引起保持架兜孔磨损、倒角处断裂失效的主要原因；

2)现有工况下载荷频率不会引起轴承保持架共振；

图16 不同圆角半径时保持架兜孔等效应力分布

3)兜孔圆角的大小对保持架应力集中有明显影响，兜孔圆角越大，兜孔等效应力极值越小。由于模具制造精度和冲压工艺的特点，很难做到兜孔圆角半径0.2 mm或0.3 mm，实际加工中的兜孔圆角半径可能超出图纸规定，因此，提高兜孔加工精度是减小兜孔等效应力极值的有效措施之一。