双横臂独立悬架前轮摆振与陀螺效应的动力学研究
2017-07-21李中好
李中好
(北京汽车研究总院有限公司,北京101300)
双横臂独立悬架前轮摆振与陀螺效应的动力学研究
李中好
(北京汽车研究总院有限公司,北京101300)
应用经典力学理论,将陀螺效应引入双横臂独立悬架动力学模型,结合虚拟样机的CAE仿真,量化分析了陀螺力矩对前轮摆振的影响。结果表明,调整车轮外倾角和前束角的变化率及其匹配关系,可解决陀螺效应引起的前轮摆振问题。
双横臂独立悬架;前轮摆振;陀螺效应
前言
前轮摆振是普遍出现在汽车上的一个相当复杂的振动现象,它对整车的操纵稳定性、舒适性、安全性和轮胎与导向机构部件的疲劳寿命均产生巨大的影响。
文献[1]~文献[5]中从车轮平衡精度、转向系统、悬架的刚度与阻尼、轮胎的侧偏刚度和前轮定位参数等方面,多角度分析了前轮摆振的影响因素。文献[6]中提出了强迫性摆振、自激性摆振、模型参数识别和高速摆振的几个主要研究发展方向。总的来说,前轮摆振的研究越来越聚焦于微观,越来越深入,但对于宏观的陀螺效应有可能产生摆振的研究仅仅停留在非独立悬架结构。文献[2]、文献[7]和文献[8]中均阐述了将陀螺效应引入整体桥来讨论前轮摆振问题,但至今未见到独立悬架引入陀螺效应的研究。
本文中通过比较两款同样结构形式的双横臂独立悬架,引入陀螺效应理论,应用ADAMS软件建立仿真模型,通过仿真计算了两款悬架的陀螺力矩,分析了其中一款悬架易出现前轮摆振的根本原因,提出了一种通过调整悬架参数瞬态变化量解决陀螺效应引起前轮摆振的方法。
1 前悬架陀螺效应的力学公式推导
1.1 悬架结构的说明简图
图1为汽车双横臂式独立悬架结构简图,该系统由5个构件组成,1为车架,2为下控制臂,3为双横臂独立悬架的转向节,4为转向横拉杆,5为上控制臂。
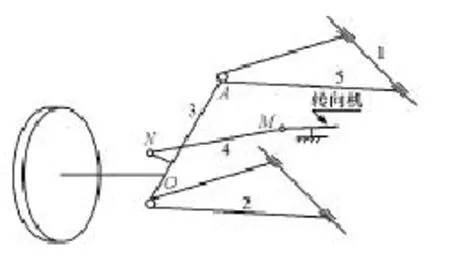
图1 双横臂独立悬架空间结构示意图
1.2 前悬架引入陀螺效应的经典理论推导结果
基于陀螺效应的理论,以左前轮为例建立如图2所示的理论分析模型,以主销轴线与车轮旋转轴线交点为坐标原点(当车轮旋转轴线与主销处于异面直线状态时,把主销轴线沿着X轴平移,对分析过程没有影响,对结果仅仅增加一个当量折算系数即可),建立如图2所示的空间三维坐标系。

图2轮胎受力与主销位置关系及陀螺效应模型示意图
图2 中,主销轴线AO延长交地面于R点。
主销内倾角α=∠BOC;主销后倾角β=∠ODE;主销与x轴夹角δ=∠AOE。令OC=1,则t

同理,主销与z轴夹角θ=∠AOC,则

车轮旋转轴线摆动方向和车轮旋转方向决定了图2中的Mz,Mx,ωx和ωz矢量方向。
陀螺效应:旋转的陀螺轴线在水平位置,其一端被支撑时,此陀螺轴即绕垂直轴缓慢的转动。此转动即为进动,此力矩即为陀螺效应进动力矩,简称陀螺力矩。陀螺效应的现象实质就是角动量定理的一个具体应用。陀螺力矩为

式中:J为车轮对其旋转轴线的转动惯量;为车轮旋转轴线的角速度;v为车辆前进行驶速度;R为车轮作用半径。
陀螺力矩、车轮轴线摆动和车轮的旋转方向符合右手定则(等同于“追矩理论”)。
由于陀螺效应作用,当车轮上下跳动时,外倾角的变化率会产生绕Z轴的陀螺力矩Mz,前束角的变化率会产生绕X轴的陀螺力矩Mx。将这两个力矩全部向主销OA上进行投影求矢量和,该力矩即为这个陀螺力矩对主销产生的旋转力矩。公式具体推导如下:
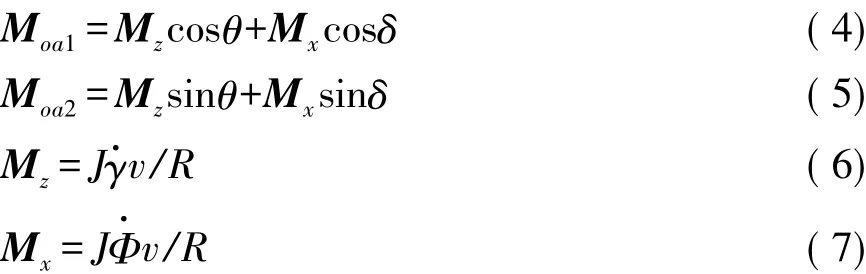
式中:γ为车轮外倾角;Φ为车轮前束角;Moa1为两个陀螺力矩向主销投影的轴向分量和;Moa2为两个陀螺力矩向主销投影的法向分量和o将式(1)、式(2)、式(6)和式(7)代入式(4)得

把式(1)、式(2)、式(6)和式(7)代入式(5)得

Moa2作用在主销上,与主销支反力平衡,对摆振不会产生直接影响。但是Moa1作用在车轮上,驱动车轮绕主销旋转,即为陀螺效应引起前轮摆振的激励源。
根据式(3)和式(8)可知:旋转的车轮加上车轮轴线的摆动就一定产生动态的陀螺力矩,二者缺一不可。车轮跳动一定引起车轮旋转轴线的摆动,车轮跳动的快慢直接影响陀螺力矩的大小。所以车轮上下跳动周期性的变化,就产生同频率的陀螺力矩,其振幅与车轮跳动时车轮旋转轴线摆动角速度的大小成正比。
陀螺力矩的方向与车轮的旋转方向和车轮旋转轴线的摆动方向相关,其方向可以通过右手定则或者是通过“追矩理论”来判断。可见在汽车行驶过程中,轮胎向上跳动和向下跳动会产生方向相反的陀螺力矩,该力矩对整车转向运动趋势的影响分为如下3种情况。
(1)当汽车的左右前轮同时受到同向垂直跳动激励时,左右车轮的陀螺力矩与车轮跳动的频率相同,左右车轮的陀螺力矩相位差180°,方向相反,故陀螺效应产生的整车转向力矩等于二者之差。在理想状态下,由于整车的左右对称、激励对称,因此产生的左右陀螺力矩大小相等,方向相反,对整车的转向运动趋势无影响。
(2)当汽车左右前轮同时受到反向垂直跳动激励时,左右车轮的陀螺力矩与车轮跳动的频率相同,左右车轮的陀螺力矩相位相同,方向相同,陀螺效应产生的整车转向力矩等于二者之和。
(3)当汽车单轮受到垂向跳动激励时,陀螺效应产生的整车转向力矩等于单侧的陀螺力矩。
2 仿真模型的建立与CAE仿真分析
2.1 双横臂独立悬架Adams仿真模型的建立
依据图表1数据,应用ADAMS软件建立两个双横臂式独立悬架动力学模型,如图3所示。
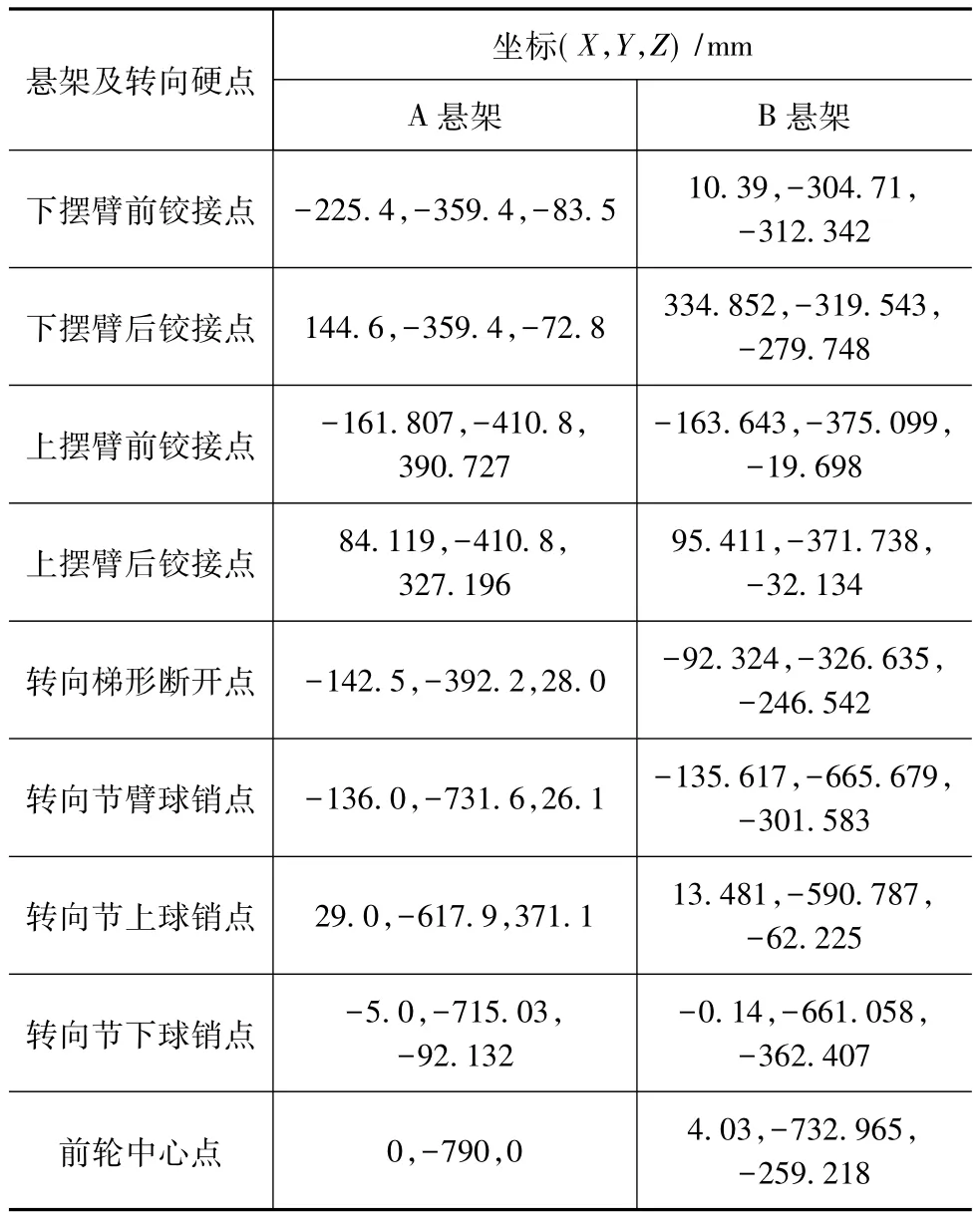
表1 双横臂独立悬架与陀螺效应相关的硬点坐标

图3 双横臂式悬架动力学分析模型
CAE模型上摆臂和下摆臂的内端通过橡胶衬套与车架连接,外端通过球铰链与转向节连接;转向横拉杆外端通过球铰链与转向节相连,内端通过等速万向节铰链与齿轮齿条转向器连接件相连;转向节通过转动铰链与车轮连接;减振器上端与车架连接,下端与下摆臂通过橡胶衬套连接。
2.2 双横臂独立悬架仿真模型计算结果分析
汽车高速行驶(100~120km/h)时前轮摆振,悬架跳动范围较小(取±25mm)。图4为该工况下A和B悬架同向跳动时外倾角与前束角的变化曲线。
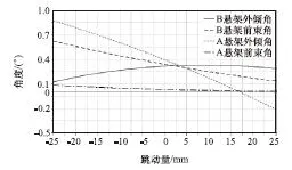
图4A和B悬架外倾角、前束角与车轮跳动曲线
由图4可以看出:(1)A悬架外倾角和前束角均是单调递减函数,它们随着车轮抬高而减小,其中外倾角变化较快,前束角变化较慢,根据上述理论可以判定,外倾角和前束角产生的陀螺力矩在主销轴线上的投影方向相同,处于数值增大的叠加状态;(2) B悬架的外倾角变化较平缓,车轮跳动量从-25到9mm区间倾角单调递增,从9到25mm区间为单调递减,车轮跳动量为9mm时,外倾角达最大值,称该点为极值点,前束角为单调递减,因此在极值点的左侧,B悬架的外倾角和前束角的陀螺力矩在主销轴线上的投影方向相反,处于相互抵消数值减少的状态,在极值点的右侧处于叠加增大状态,优化调整极值点的位置可使整车在高速工况,悬架的跳动工作区域内交变的陀螺力矩最小。
图5为A和B悬架陀螺力矩系数变化曲线,它是根据外倾角和前束角的变化量,按照式(8)计算出的相对结果。在悬架跳动周期相同的情况下,A和B悬架在车轮处于平衡位置的瞬间陀螺力矩系数分别为-21.22和2.49,正负号仅仅表示陀螺力矩方向相反。该结果表明在同样条件下A悬架产生的陀螺力矩为B悬架的8.52倍,即A悬架在车轮上下跳动时,产生的绕主销旋转的驱动激励力矩为B悬架的8.52倍。也即A悬架的摆振能量约比B悬架大8倍。

图5A和B悬架陀螺力矩系数变化曲线图
2.3 陀螺力矩对双横臂独立悬架前轮摆振的影响分析
由文献[9]可知:

式中:ζ为相对阻尼系数;v为车辆前进行驶速度;l为整车轴距;C1为前轮侧偏刚度系数(侧偏刚度与轴荷之比);C2为后轮侧偏刚度系数(侧偏刚度与轴荷之比)。
高速行驶的汽车,陀螺力矩的能量,再叠加上其它促使前轮绕主销旋转的激励能量(车轮不平衡力和力矩,地面的激励,轮胎的自激振动等)共同驱动前轮绕主销往复振动。由式(10)可知:转向系统的相对阻尼系数随着车速的升高而减小;转向盘小转角范围又是整个转向系统的低刚度、低阻尼区域[9]。因此这个往复振动很容易克服转向系统的刚度和阻尼向上传递到转向盘,造成转向盘的切向角振动,即产生摆振。
上述推导的陀螺力矩公式和CAE仿真结果表明:A悬架由于本身结构产生的陀螺力矩比B悬架大,具有比较大的摆振能量,所以在整车的高速行驶过程中,很容易满足摆振模态的触发条件,产生摆振。此时,即使轮胎动不平衡量为零,装配A悬架的车辆仍然会出现前轮摆振,与此相反,即使装配轮胎动平衡量有点超差的B悬架,在具体使用过程中也不易出现前轮摆振现象。
可见,降低陀螺效应引起的摆振能量就能有效降低前轮摆振的故障发生率,能够彻底解决以陀螺效应作为主要原因的前轮摆振。
3 结论
通过调整与陀螺效应相关的悬架和转向系统硬点,可降低双横臂独立悬架的陀螺效应而产生的摆振能量。调整硬点的依据准则如下:
(1)降低悬架上下跳动过程中前轮外倾角和前束角的变化率;
(2)在满足悬架性能的基础上调整外倾角和前束角的变化趋势,使二者产生的陀螺力矩在主销轴线上的分量方向相反,相互抵消,达到减弱陀螺效应的不良影响。
参考资料
[1]贺丽娟,林逸.汽车操纵稳定性与前轮摆振的非线性仿真分析[J].汽车工程,2007,29(5):389-392.
[2]秦浩董,笑鹏.浅析汽车前轮摆振问题的非故障原因[J].农业装备与车辆工程,2008(9):27-28.
[3]贺丽娟,李欣业,等.非独立悬架车辆自激摆振的数值仿真分析[J].计算机仿真,2008,25(2):269-273.
[4]林逸,贺丽娟.汽车前轮摆振非线性研究综述[J].农业机械学报,2007,38(11):174-177.
[5]李欣业,贺丽娟,董正身,等.解放CA10型载货汽车前轮摆振的数值仿真研究[J].汽车工程,2004,26(5):585-587.
[6]李胜,林逸.汽车转向轮摆振研究[J].汽车技术,2004(11):16-19.
[7]小林明.汽车振动学[M].北京:机械工业出版社,1976.
[8]张楠,张建润,孙蓓蓓,等.汽车振动与噪声控制[M].北京:人民交通出版社,2005.
[9]郭孔辉.汽车操纵动力学[M].长春:吉林科学技术出版社,1991.
A Dynamics Study on Front Wheel Shimmy and Gyroscopic Effect in Double Wishbone Suspension
Li Zhonghao
Beijing Automotive Technology Center,Beijing101300
By applying classical mechanics theory,the gyro effect is introduced into the dynamic model of double wishbone suspension,and combined with CAE simulation of virtual prototype,the effects of gyro torque on front wheel shimmy is quantitatively analyzed.The results show that through the adjustment of the changing rates of wheel camber and toe and their matching relationship,the issue of front wheel shimmy caused by gyro effect can be resolved.
double wishbone independent suspension;front wheel shimmy;gyroscope effect
10.19562/j.chinasae.qcgc.2017.06.014
原稿收到日期为2016年6月7日,修改稿收到日期为2016年8月31日。
李中好,高级工程师,E-mail:lizhonghaolzh@163.com。
